Термодинамика и статистическая физика Лекции по термодинамике

Термодинамика и статистическая физика Лекции по термодинамике

Новицкий Андрей Викторович Кафедра теоретической физики и астрофизики novitsky@bsu. by

Содержание курса • Термодинамика (3 -4 лекции) • Вспомогательные вопросы (1 лекция) • Статистическая физика (30 лекций) – основы стат. физики – примеры распределений • Больцмана, Максвелла • Ферми, Дирака – примеры физических систем • фотонный и электронный газы • твердое тело • идеальный и неидеальный газы 3

Литература • • • Л. Д. Ландау и Е. М. Лифшиц, Статистическая физика. Часть 1. (Том 5). – М. : Наука, 1976. Р. Кубо, Статистическая механика. – М. : Мир, 1967. Р. Кубо, Термодинамика. – М. : Мир, 1970. И. П. Базаров, Термодинамика. - М. : Высшая школа, 1991. Ч. Киттель, Элементарная статистическая физика. – М. : Издво иностр. лит. , 1960. К. А. Путилов, Термодинамика. – М. : Наука, 1971. 4

Статистическая физика • Предметом статистической физики является изучение закономерностей, которым подчиняются поведение и свойства макроскопических тел, состоящих из большого количества частиц – атомов и молекул – Классическая статистика – Квантовая статистика • Большое количество частиц позволяет говорить об усредненных, статистических закономерностях систем 5

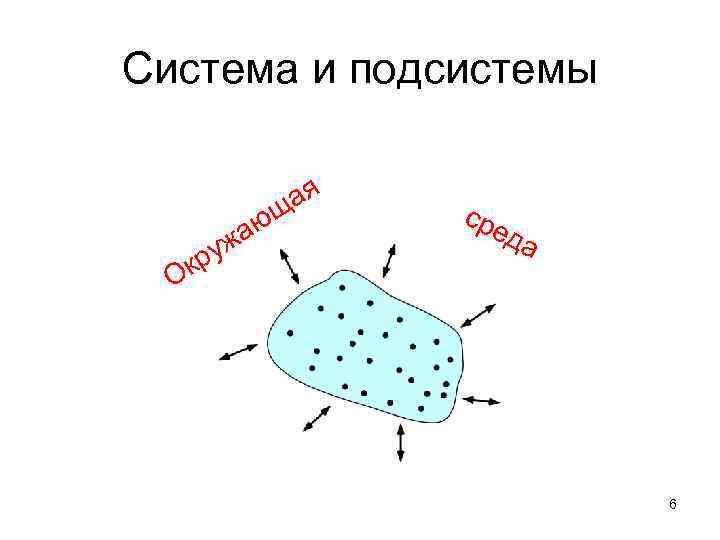Система и подсистемы аю ая щ уж кр сре да О 6

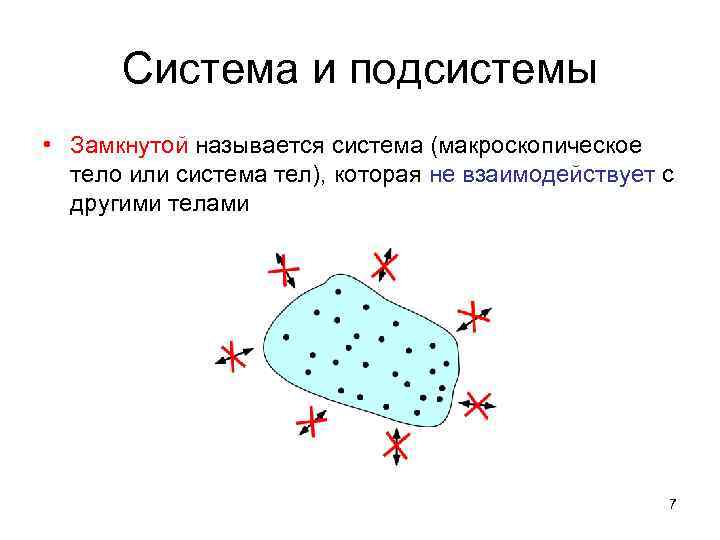Система и подсистемы • Замкнутой называется система (макроскопическое тело или система тел), которая не взаимодействует с другими телами 7

Система и подсистемы • В замкнутой системе можно выделить малую область, в которой все же чрезвычайно много частиц. Эта область называется подсистемой. • Движение подсистемы сложное из-за взаимодействия с другими частями системы. 8

Система и подсистемы • В замкнутой системе можно выделить малую область, в которой все же чрезвычайно много частиц. Эта область называется подсистемой. • Однако в течение достаточно малых промежутков времени подсистемы можно считать (квази)замкнутыми. Взаимодействие проявляется на больших временах и для малого количества частиц в подсистеме 9

Термодинамика

Содержание • • • Энтропия. Температура и давление Первое, второе и третье начало термодинамики Теплоемкость Термодинамические потенциалы Термодинамические тождества и неравенства Максимальная работа Принцип Ле-Шателье Цикл Карно Переменное число частиц 11

Термодинамика • Предметом термодинамики является описание и характеризация макроскопических состояний тел в статистическом равновесии (нет взаимодействия!) • Сначала система описывается методами статистики, а затем ей сопоставляются некоторые макроскопические параметры (температура, давление, теплоемкость) • При этом поведение системы многих частиц будет задаваться уравнением состояния, связывающим термодинамические характеристики (например, уравнение состояния идеального газа p. V=Nk. T) 12

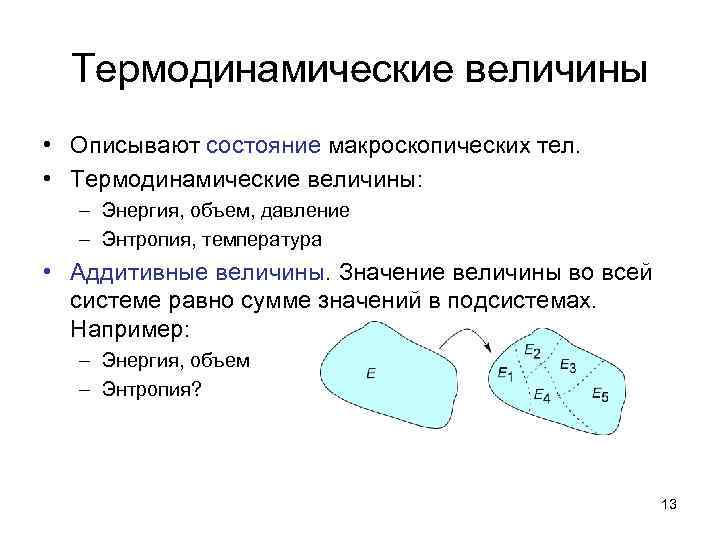Термодинамические величины • Описывают состояние макроскопических тел. • Термодинамические величины: – Энергия, объем, давление – Энтропия, температура • Аддитивные величины. Значение величины во всей системе равно сумме значений в подсистемах. Например: – Энергия, объем – Энтропия? 13

Энтропия • В статистике задается как логарифм статистического веса системы (количества состояний в системе) – мера вероятности реализации макроскопического состояния. • Число состояний равно произведению числа состояний каждой из подсистем • Энтропия системы равна сумме энтропий каждой из подсистем и потому аддитивная величина 14

Энтропия • В статистике задается как логарифм статистического веса системы (количества состояний в системе). • Энтропия как мера беспорядка в системе. Отрицательная энтропия – мера информации 15

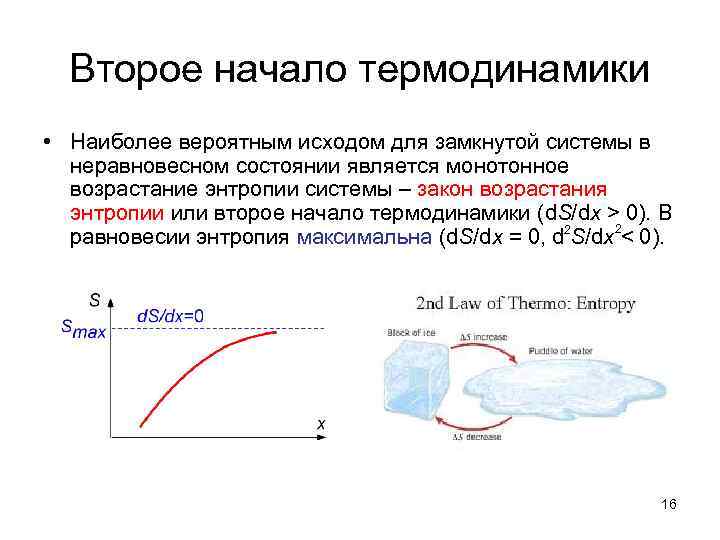Второе начало термодинамики • Наиболее вероятным исходом для замкнутой системы в неравновесном состоянии является монотонное возрастание энтропии системы – закон возрастания энтропии или второе начало термодинамики (d. S/dx > 0). В равновесии энтропия максимальна (d. S/dx = 0, d 2 S/dx 2< 0). 16

Второе начало термодинамики. Формулировка Клаузиуса • Тепло никогда не может переходить от холодного к горячему, если для этого нет специальных причин (1854) • Термодинамическое определение энтропии • Неравенство Клаузиуса – эквивалент закона возрастания энтропии 17

Температура • Замкнутая система: 2 тела в тепловом равновесии друг с другом • Энтропия равновесной системы максимальна • Тогда Абсолютная температура тел не может быть отрицательной! 18

Неравновесный процесс • Возрастание энтропии Энергия переходит от тел с высокой температурой к телам с низкой температурой 19

Давление • Сила, с которой тело, состоящее из N частиц, действует на границу своего объема: Задание. Вывести определение давления, исходя из максимальности энтропии в равновесном состоянии 20

Первое начало термодинамики • Аддитивность энергии и энтропии приводит к тому, что E(S=const) или S(E=const) не зависят от формы тела, а только от объема V • Макроскопическое состояние равновесной системы определяется двумя величинами, например, энтропией S и объемом V (число частиц считаем постоянным) 21

Первое начало термодинамики • Макроскопическое состояние равновесной системы определяется двумя величинами, например, энтропией S и объемом V (число частиц считаем постоянным) 22

Работа и количество тепла • • Не полный дифференциал Функция процесса, а не состояния Интеграл по циклу отличен от нуля Положительная работа – работа, производимая телом над внешними объектами (при расширении), отрицательная работа – работа внешних объектов • Положительное количество тепла – тепло, полученное телом извне • 23

Теплоемкость • Количество тепла, при получении которого температура тела повышается на единицу • В зависимости от условий различают – при постоянном объеме – при постоянном давлении - энтальпия 24

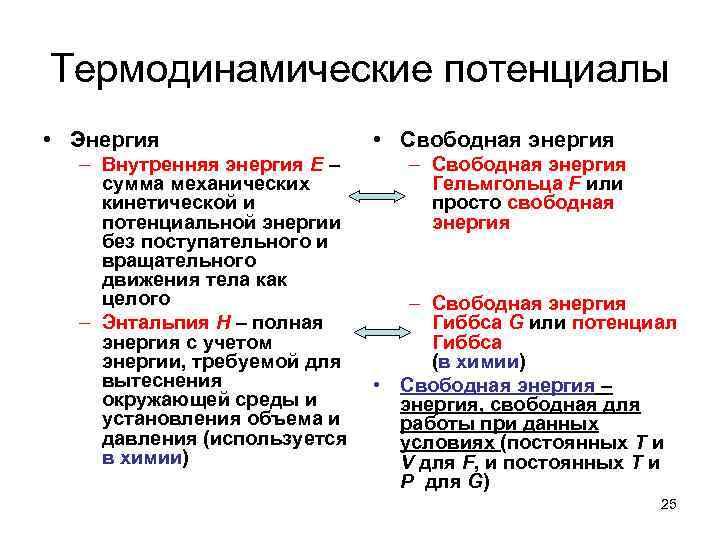Термодинамические потенциалы • Энергия – Внутренняя энергия E – сумма механических кинетической и потенциальной энергии без поступательного и вращательного движения тела как целого – Энтальпия H – полная энергия с учетом энергии, требуемой для вытеснения окружающей среды и установления объема и давления (используется в химии) • Свободная энергия – Свободная энергия Гельмгольца F или просто свободная энергия – Свободная энергия Гиббса G или потенциал Гиббса (в химии) • Свободная энергия – энергия, свободная для работы при данных условиях (постоянных T и V для F, и постоянных T и P для G) 25

Энтальпия ххххх • Преобразование Лежандра При P=const : При V=const : 26

Свободная энергия хххх Гельмгольц При T=const: Зная свободную энергию, можно найти внутреннюю энергию 27

Потенциал Гиббса При P=const и T=const: х 0 Задание. Чему равна энтальпия H как функция потенциала Гиббса G? 28

Изменение свободной энергии при необратимых (химических) реакциях • В равновесном процессе • В неравновесном процессе • При T=const, V=const • При T=const, P=const • В равновесии свободная энергия минимальна! Реакция алмаз -> графит происходит с уменьшением свободной энергией Гиббса, но настолько медленно, что не заметно 29

Теорема о малых добавках • Если есть параметры энергия равна и функции , то • Другие потенциалы изменяются так же, например, 30

Примеры • Расстояние L • Электрическое поле E • Магнитное поле H • Сила F • Поляризация P • Намагниченность M Скажем, для частиц во внешнем электрическом поле записываем Если мы вычислили, например, свободную энергию F из соображений статистики, то поляризация среды равна Поляризуемость среды вычисляется согласно 31

Термодинамические тождества • Тождества, позволяющие найти значения величин по уравнению состояния тела и теплоемкости • Уравнение состояния – уравнение, связывающее давление, объем и температуру, P=P(V, T) • Какие величины можно найти? 32

Методы доказательства тождеств • Первое начало термодинамики • Соотношения Максвелла – выводятся из условия независимости вторых частных производных от порядка дифференцирования • Якобианы – свойства якобианов устанавливают связи между частными производными 33

Соотношения Максвелла • Для внутренней энергии записываем или 34

Термодинамическая шкала температуры • Абсолютная температура Т(τ) • Под действием тепла изменяется объем V и температура τ термометра • Используя соотношение Максвелла и выражение , получаем Выбор единиц шкалы произволен! Абсолютная температура не меняет знак – положительна! 35

Якобианы. Свойства • Определение якобиана для функций u(x, y) и v(x, y) 1. 2. 3. 4. 36

Якобианы. Пример. Cp-Cv=? 1 4 • Уравнение состояния P=P(V, T) при T=const будет P=P(V), поэтому • Поскольку (например, для идеального газа ), то 37

Якобианы. Пример. Cp/Cv=? 1 4 4 1 Адиабатическая сжимаемость по модулю всегда меньше изотермической сжимаемости, потому что Cp>Cv 38

Процессы • Квазиравновесные процессы – – Изотермический T=const Изобарический P=const Изохорический V=const Адиабатический S=const в теплоизолированной системе • Обратимый – энтропия замкнутой системы остается постоянной • Необратимый – энтропия замкнутой системы возрастает. Поскольку энтропия не может убывать, то процесс не может повториться в обратном порядке 39

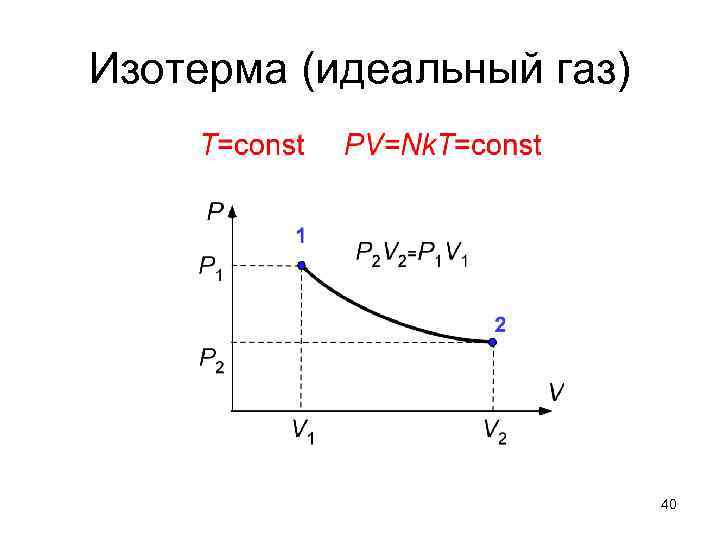Изотерма (идеальный газ) 40

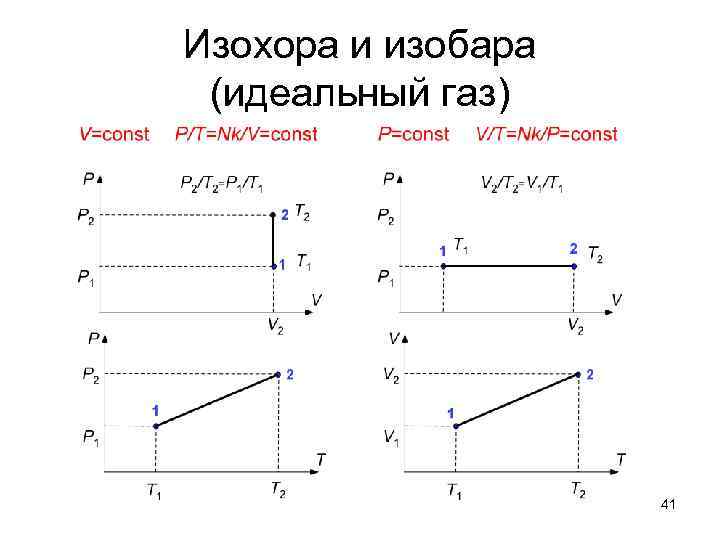Изохора и изобара (идеальный газ) 41

Теплоизолированная система • Система теплоизолирована, если она не подвергается никаким воздействиям, кроме изменения внешних условий, к которым относятся – Изменение объема тела – Внешние поля (например, электромагнитные) • Теплоизолированное тело не замкнутая система, потому что внешнее поле вводит явную зависимость от времени в функцию Гамильтона E=H(p, q, t) • Внешнее поле – механический, а не статистический объект, поэтому его энтропия равна нулю, и закон возрастания энтропии выполняется для теплоизолированных систем 42

Адиабатический процесс • Медленное воздействие внешних условий на теплоизолированное тело • Пусть замкнутая система подвержена внешнему воздействию, описываемому параметром λ(t). Тогда • Энтропия тела остается неизменной, то есть адиабатический процесс обратим. Однако не всякий обратимый процесс адиабатичен, потому что постоянной должна быть энтропия тела, а не всей замкнутой системы 43

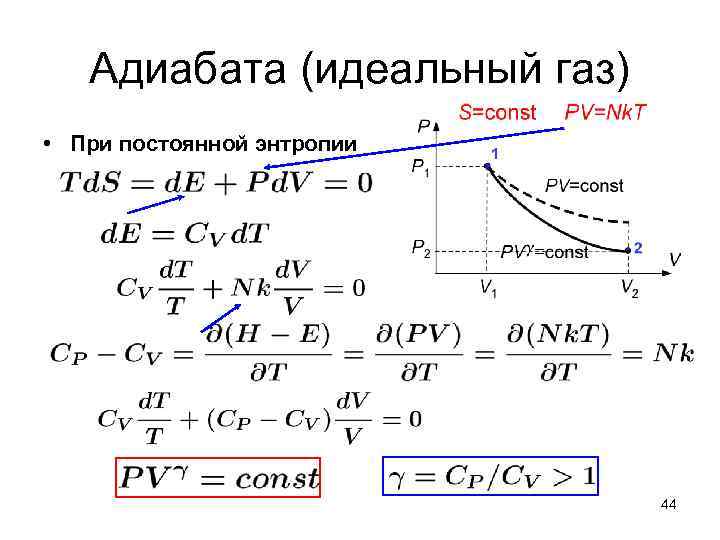Адиабата (идеальный газ) • При постоянной энтропии 44

Необратимый процесс Джоуля-Томсона • Теплоизолированный газ (жидкость) переводится из сосуда под давлением P 1=const в сосуд под давлением Р 2=const через пористую перегородку • Поскольку d. H=Td. S+Vd. P=0, то энтальпия сохраняется, H 1=H 2. Энтропия при уменьшении давления возрастает: • При расширении газа в пустоту сохраняется энергия Е и энтропия увеличивается: Задание. Вычислить для процесса Джоуля-Томсона. 45

Термодинамические неравенства • В положении равновесия максимум энтропии, поэтому мы уменьшаем энтропию при малом отклонении, т. е. • Разлагая в ряд вблизи положения равновесия, имеем 46

Термодинамические неравенства • Из первого неравенства следует, что теплоемкость при постоянном объеме положительна: • Из второго неравенства выводим, что увеличение объема сопровождается уменьшением давления 47

Термодинамические неравенства • Из первого неравенства следует, что теплоемкость при постоянном объеме положительна: • Из второго неравенства выводим, что увеличение объема сопровождается уменьшением давления • Когда неравенства не выполняются, состояния неустойчивы и не могут существовать в природе • Неравенства выполняются только для однородных тел Задание. Какое неравенство следует для ? 48

Максимальная работа • Работа за счет неравновесности в теплоизолированной системе следует из законов сохранения энергии и возрастания энтропии • Переход в равновесное состояние должен совершаться обратимым образом, с постоянной энтропией • Таким образом, работа максимальна при неизменной энтропии, т. е. в обратимых процессах – При переходе из неравновесного состояния в равновесное – Тело во внешней среде 49

Цикл Карно • Передача энергии δQ непосредственно от одного тела к другому невозможно обратимо, потому что энтропия увеличивается на δQ/T 1 - δQ/T 2. Чтобы получить максимальную работу – нужно третье (рабочее) тело, – при обмене энергией тела должны находиться при одинаковой температуре, чтобы энтропия в этом процессе не менялась – изменение температуры должно происходить адиабатически, без изменения энтропии, – рабочее тело производит максимальную работу, работая по обратимому циклу. • КПД цикла будет максимальным, потому что максимальна работа, совершаемая по обратимому циклу 50

Цикл Карно • КПД цикла будет максимальным, потому что максимальна работа, совершаемая по обратимому циклу 51

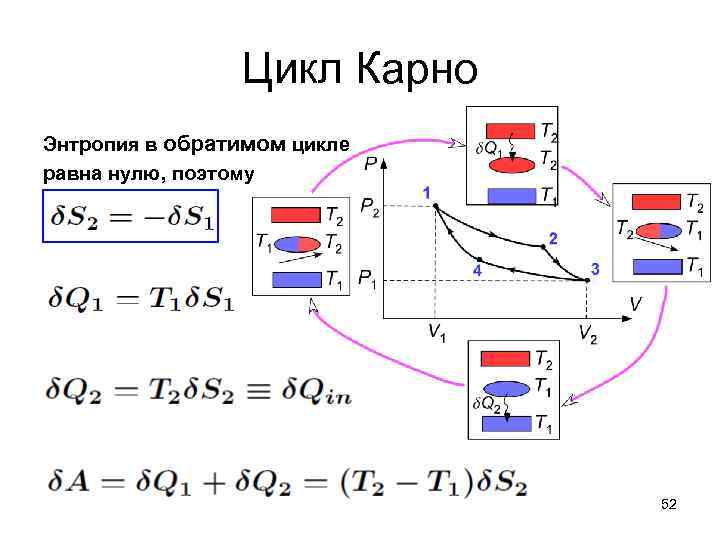Цикл Карно Энтропия в обратимом цикле равна нулю, поэтому 52

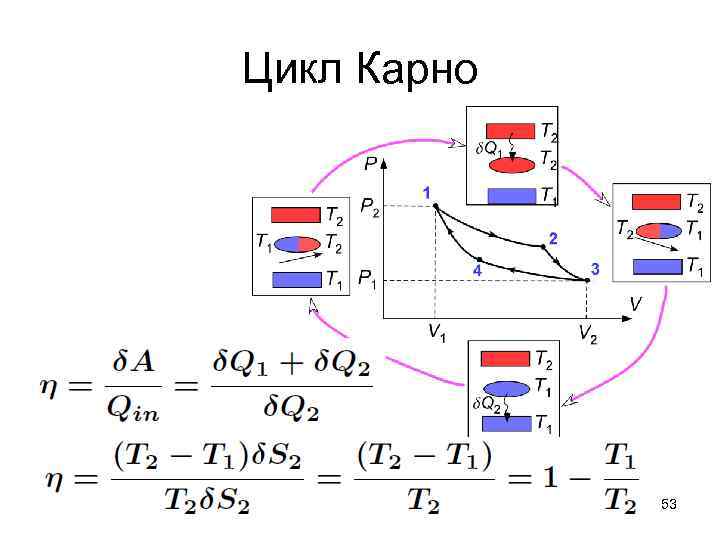Цикл Карно 53

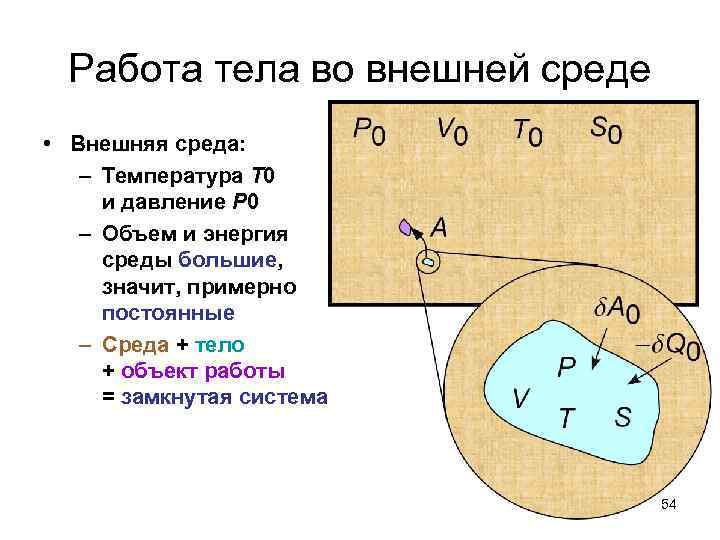Работа тела во внешней среде • Внешняя среда: – Температура T 0 и давление P 0 – Объем и энергия среды большие, значит, примерно постоянные – Среда + тело + объект работы = замкнутая система 54

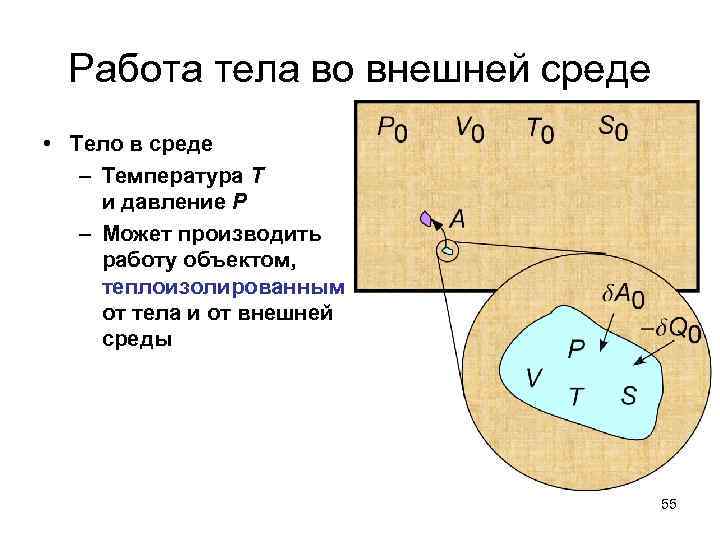Работа тела во внешней среде • Тело в среде – Температура T и давление P – Может производить работу объектом, теплоизолированным от тела и от внешней среды 55

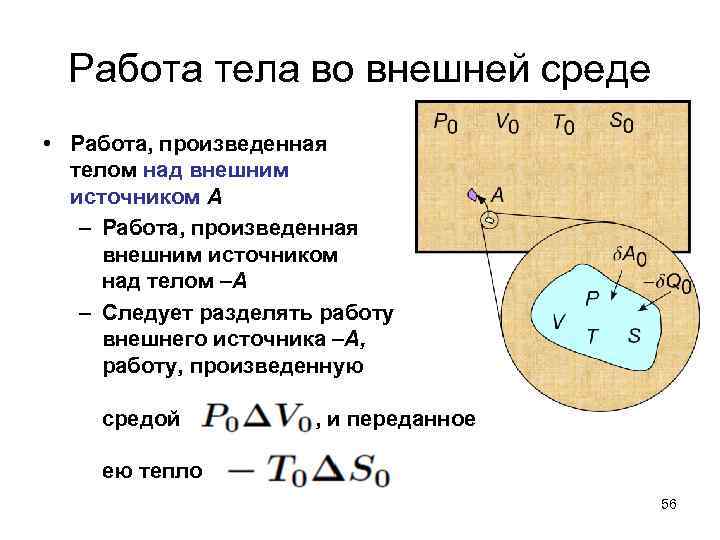Работа тела во внешней среде • Работа, произведенная телом над внешним источником А – Работа, произведенная внешним источником над телом –А – Следует разделять работу внешнего источника –А, работу, произведенную средой , и переданное ею тепло 56

Максимальная работа во внешней среде • Закон сохранения энергии Изменение внутренней энергии внешней среды Изменение внутренней энергии тела Работа, производимая телом 57

Максимальная работа во внешней среде Обратимый процесс: F и G – энергия, свободная для совершения работы 58

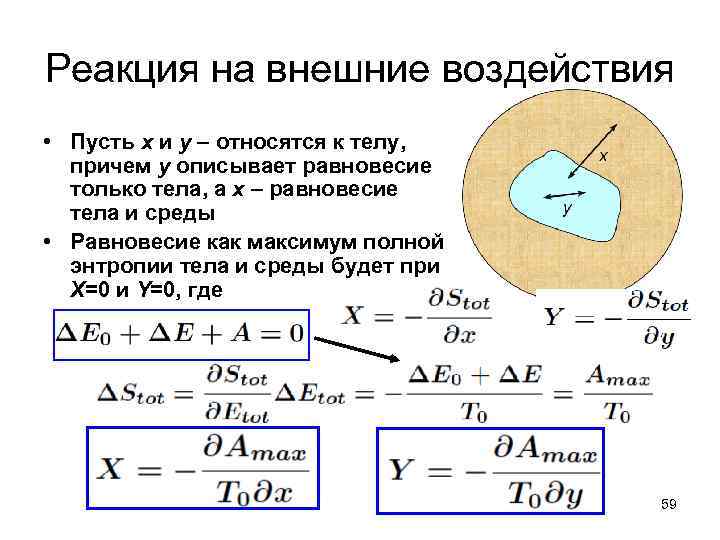Реакция на внешние воздействия • Пусть х и у – относятся к телу, причем у описывает равновесие только тела, а х – равновесие тела и среды • Равновесие как максимум полной энтропии тела и среды будет при Х=0 и Y=0, где 59

Отклонение от равновесия • Отклонение от равновесия соответствует уменьшению энтропии S(x, y) Равновесие: 60

Принцип Ле-Шателье • При изменении равновесия тела со средой • После установления равновесия снова, Х станет отличным от нуля Принцип Ле-Шателье: внешнее воздействие, выводящее тело из равновесия, стимулирует в нем процессы, стремящиеся ослабить 61 результаты этого воздействия

Принцип Ле-Шателье. Пример 1 • Пусть в качестве величин выбраны энтропия и объем 62

Принцип Ле-Шателье. Пример 1 • Пусть в качестве величин выбраны энтропия и объем 63

Принцип Ле-Шателье. Пример 2 • Теперь выберем объем и энтропию: 64

Принцип Ле-Шателье. Пример 2 • Теперь выберем объем и энтропию: 65

Положительность температуры • При T<0 невозможно существование равновесных тел (Ландау, Лифшиц) • Неравенство T>0 можно доказать из закона возрастания энтропии – энтропия имеет максимум при Для абсолютной температуры существует минимум T=0!66

Положительность температуры • При T<0 невозможно существование равновесных тел (Ландау, Лифшиц) • Неравенство T>0 можно доказать из закона возрастания энтропии • Для абсолютной температуры существует минимум T=0! • Температура может быть отрицательной только в неполном равновесии и соответствует части степеней свободы тела. Например, для замкнутой системы двух тел 67

Теорема Нернста • Низкой температуре соответствует низкая энергия. При абсолютном нуле это будет одно, основное состояние • Тогда энтропия как логарифм числа состояний (ln 1 = 0) равна нулю при абсолютном нуле температуры (теорема Нернста или третье начало термодинамики, 1906) • Следствие квантовой статистики! • Если уменьшать температуру и плотность газа, то теорема Нернста может не выполняться! Нужны постоянные объем или давление • В частности, можно показать, что при T=0 68

Вычисление величин • Из теоремы Нернста мы знаем значения постоянной интегрирования по температуре, так как есть температурный минимум • Например, при постоянном объеме находим Задание. Вычислить величины при постоянном давлении 69

Зависимость от числа частиц, как от параметра • Из аддитивности величин S и V можно сделать вывод о зависимости термодинамических потенциалов от числа частиц N E 1 – энергия на 1 частицу, характеризующуюся объемом V 1 70 и энтропией S 1

Переменное число частиц • Пусть внутренняя энергия зависит не только от энтропии и объема, но и от числа частиц, которое может меняться в системе. Тогда Химический потенциал Задание. Вывести обобщенные соотношения Максвелла. 71

Большой термодинамический потенциал • Рассмотрим постоянный объем V, число частиц N в котором может меняться. Тогда для свободных энергий 72

Большой термодинамический потенциал • Рассмотрим постоянный объем V, число частиц N в котором может меняться Задание. Показать, что при постоянных температуре, объеме и химическом потенциале работа при обратимом процессе равна изменению большого термодинамического потенциала. 73

Условие равновесия при переменном числе частиц • Пусть 2 подсистемы образуют замкнутую систему и могут обмениваться только частицами, а все другие величины постоянны. Тогда Во внешнем потенциальном поле Например, в поле тяжести получаем формулу гидростатического давления 74