Термодинамическое равновесие поверхностного слоя Для равновесия замкнутой системы

Термодинамическое равновесие поверхностного слоя Для равновесия замкнутой системы, состоящей из I и II объемных фаз должно соблюдаться условие: - изменение внутренней энергии поверхностного слоя τ –толщина 1

Рассмотрим два важных случая: 1) Поверхность раздела не изменяется; 3 Т Складываем 2

Система замкнута, внешние условия наложенные на нее: (5) ………………. Кроме условия (5) еще и Учитывая (4) общие условия можно свести к: 3

Таким образом, условия термического и химического равновесия аналогичны условиям равновесия объемных фаз: В поверхностных слоях будем говорить не о всей внутренней энергии или энтропии поверхностного слоя и не о всем количестве каждого компонента, а лишь о избытке. Именно эти избытки и характеризуют отличие поверхности от объемных фаз: - полная поверхностная энергия 4

Тогда 2) Поверхность раздела меняется: где поверхностное натяжение, аналогично давлению в объемной фазе ( ) Если P эрг/см 3 или дин/см 2, то σ- эрг/см 2 или дин/см. Смещение поверхности S вызывает изменение объема соседних фаз I и II на и , причем 5

Эти изменения вызовут дополнительные изменения и на и Общее изменение энергии, связанное со смещением поверхности S при равновесии равно 0, поэтому Это условие механического равновесия: Это выражение показывает, что в случае возможности изменения смещения поверхности S гидростатические давления в обьемных средах не равны другу. 6

7

8

Это уравнение показывает, что разность гидростатических давлений в смежных фазах равна произведению σ на d. S. , если плоская поверхность раздела, т. е. k 1=k 2=0 9

Частные случаи 1. Давление газа внутри сферического пузырька. 10

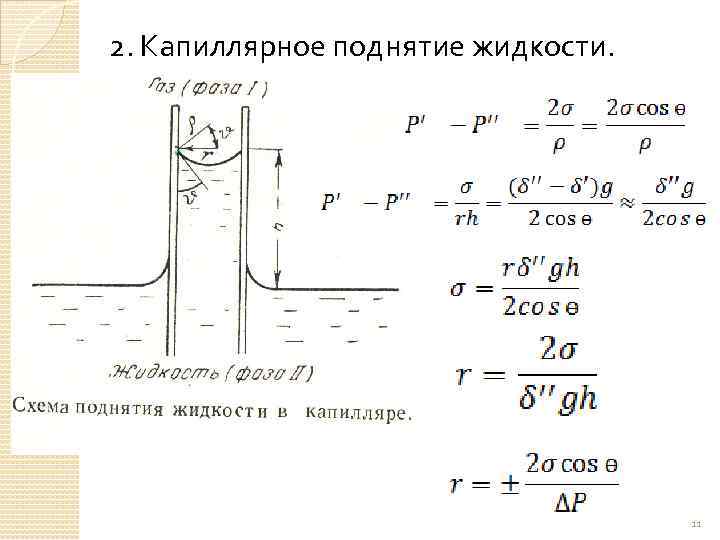2. Капиллярное поднятие жидкости. 11

Физическая адсорбция на непористых твёрдых телах Уравнение изотермы адсорбции Генри Адсорбционное равновесие: Молекула в газе молекула на адсорбенте (адсорбционный комплекс) Са – концентрация в адсорбционном слое γa - коэффициент активности в адсорбционном слое 12

(1) Так как К=const при Т при невысоких концентрациях в газовой фазе γ=1 (2) 13

В случае сильной адсорбции даже при малых с γa ≠ 1. γa =1 в случае малой сорбируемости, то есть при малой са (3) Для идеальных газов 14

Это простейшие уравнения изотермы сорбции, это уравнения Генри, а К = константа Генри Вместо са удобно пользоваться Θ - степень заполнения 15

16

17

Уравнения изотермы адсорбции Ленгмюра Адсорбция мономолекулярная и локализованная молекула газа + свободное место на поверхности локализованный адсорбционный комплекс 18

19

20

Пренебрегаем взаимодействиями адсорбат-адсорбат Тогда константа равновесия 21

(4) 22

(5) или Проанализируем при малых значениях р (уравнение Генри) при больших значениях р 23

am – ёмкость монослоя (6) 24

25

поверхностная концентрация (7) 26

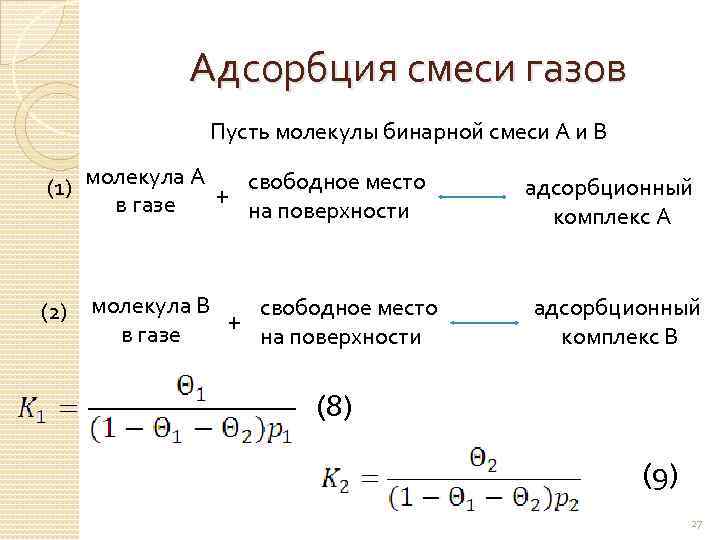Адсорбция смеси газов Пусть молекулы бинарной смеси А и В (1) молекула А + свободное место в газе на поверхности (2) молекула В + свободное место в газе на поверхности адсорбционный комплекс А адсорбционный комплекс В (8) (9) 27

(10) определим получим и подставим в (8) и (9) (11 а) (11 б) если i-компонентов (11 в) 28

Уравнения изотермы полимолекулярной адсорбции Брунауэра, Эммета и Теллера (БЭТ) при p=ps начинается объёмная конденсация Используем те же допущения, что при выводе уравнения Ленгмюра 29

30

Кинетическая модель сорбции молекула газа + свободная поверхность единичные комплексы + единичный комплекс двойные комплексы + двойной комплекс тройные комплексы и т. д. 31

Θ 1, Θ 2, Θ 3 – доли поверхности, занятые единичными, двойными и тройными комплексами Θ 0 – доля свободных мест на поверхности Скорость конденсации на первом слое (12) Скорость испарения 32

(13) Для 2 -го слоя 33

- Кинетическая теория газов 34

35

36

Уравнение БЭТ 37

Спрямление 38

39

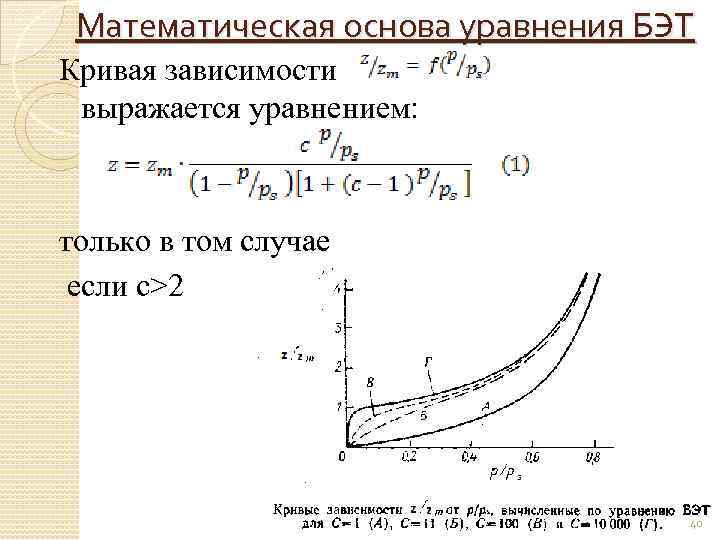Математическая основа уравнения БЭТ Кривая зависимости выражается уравнением: только в том случае если с>2 40

Расчленяем правую часть выражения: кривую зависимости можно при этом получить как разность двух гипербол, выражается уравнением: 41

(3) Имеет асимптоты при пересекает ось (4) Имеет асимптоты при кривая пересекает ось в к выраженной кривой и и и 42

Если с<2, то изотерма переходит в изотерму III типа: Точка перегиба: 43

44

Проявление притяжений адсорбат - адсорбат Для разветвленных молекул СCl 4, С(СH 3)4 на неполярной поверхности эти взаимодействия проявляются довольно сильно. Это проявляется в отклонении от 1 коэффициента активности γа и в увеличении теплоты адсорбции на однородной поверхности с увеличением степени заполнения: Зависимость ө от γа - приближенно Введем в уравнение Ленгмюра 45

46

Решим его относительно Наиболее простое уравнение локализованной адсорбции на однородной поверхности, учитывающее взаимодействие адсорбат, уравнение Киселева При k 1=0, уравнение переходит в уравнение Ленгмюра. 47

48