лек 8 Основы и матем. описание теплообм БАФ.ppt
- Количество слайдов: 44

Тепловые процессы Основные понятия и определения теории теплообмена

Основы теплообмена § Самопроизвольный необратимый процесс переноса § § § энергии в форме теплоты в пространстве называют теплообменом. Существует три основных вида теплообмена: теплообмен теплопроводностью, конвективный теплообмен, теплообмен излучением. Теплообмен очень часто сопровождается массобменом. . Если концентрации компонентов в различных точках пространства разные, происходит необратимый перенос массы компонентов из одной области в другую. Этот процесс называется массообменом. Совместно протекающий процесс переноса теплоты и массы вещества называют тепломассообменом. Как и любой реальный самопроизвольный процесс тепломассообмен является необратимым и продолжается до тех пор, пока в системе не установится термодинамическое равновесие.

Теплопроводность § Перенос энергии (теплоты) при непосредственном § § § контакте более нагретых элементов тела (или среды) с менее нагретыми, осуществляемый посредством хаотического движения микрочастиц (молекул, атомов, электронов, ионов), называют теплопроводностью. Материалы обладают различной способностью проводить теплоту. Наибольшей способностью обладают металлы. Их теплопроводность при не очень низких температурах в основном обуславливается тепловым движением электронов. Причем, чем меньше удельное электрическое сопротивление металла, тем выше его теплопроводность.

Теплопроводность § Газы плохие проводники теплоты. Теплопроводность газов обусловлена хаотическим тепловым движением молекул. Она возрастает с увеличением температуры, так как при этом увеличивается скорость теплового движения молекул. § В диэлектриках передача теплоты происходит посредством колебаний узлов кристаллической решетки, а в жидкостях - за счет упругих колебаний молекул и их перескока из одного положения в другое.

Конвективный теплообмен В движущихся жидкостях и газах происходит конвективный теплообмен. В этом случае распространение энергии в пространстве осуществляется одновременно двумя способами: § за счет теплового движения микрочастиц и § посредством перемешивания микрочастиц (элементов жидкости или газа) из одной точки пространства в другую. Последний способ называют конвективным переносом теплоты.

Конвективный теплообмен Перенос тепла возможен в условиях естественной (свободной) или вынужденной конвекции. Естественная конвекция происходит, например, за счет разности плотностей в различных точках объема жидкости (или газа), возникшей вследствие разности температур в этих точках (термогравитационная конвекция). Вынужденная конвекция происходит под действием внешних сил принудительном движении всего объема жидкости (или газа). Возможен также теплообмен при смешанной конвекции. Конвективный теплообмен между движущейся средой и омываемой ею поверхностью твердого тела называют теплоотдачей.

Теплообмен излучением (радиационный теплообмен) Третий вид теплообмена - теплообмен излучением включает в себя совокупность процессов: § превращение внутренней энергии вещества в энергию излучения (энергию электромагнитных волн или фотонов) – процесс лучеиспускания; § перенос излучения; § поглощение излучения веществом – процесс лучепоглощения.

Сложные виды теплообмена Перенос энергии одновременно § излучением и § теплопроводностью называется радиационно-кондуктивным теплообменом, Перенос энергии одновременно § излучением, § теплопроводностью и § конвекцией называется радиационно-конвективным теплообменом.

Особенности описания тепломассопереноса Для теоретического изучения процессов тепломассопереноса на основе общих законов физики составляется их математическое описание. При этом среду, в которой протекают эти процессы, считают сплошной. Это значит, что в физически бесконечно малом элементе V (элементарном объеме) содержится очень большое число микрочастиц. Под V понимается такой объем, размеры которого пренебрежимо малы по сравнению с характерным геометрическим размером (например, с диаметром трубы).

ТАКИМ ОБРАЗОМ Перенос энергии в форме теплоты может осуществляться тремя способами: § теплопроводностью; § конвекцией; § излучением (радиацией). Совокупность всех трех видов теплообмена называется сложным теплообменом.

Еще термины… • Горячее тело или вещество, участвующее в процессе теплообмена называют горячим теплоносителем. • Нагреваемое вещество называют холодным теплоносителем. • Чаще всего теплота передается через стенку, разделяющую теплоносители. Эту стенку называют поверхностью теплообмена.

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССА ТЕПЛОПРОВОДНОСТИ В начале введем некоторые понятия, которыми будем оперировать при описании процесса теплопередачи теплопроводностью: - температурное поле; - градиент температуры; - тепловой поток - коэффициент теплопроводности - коэффициент температуропроводности 12

Температурное поле К числу основных задач теплообмена относится установление зависимости между тепловым потоком и распределением температур в средах. Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем. В зависимости от конфигурации изучаемой области пространства (т. е. от формы тела) выбирают декартову, цилиндрическую или сферическую системы координат. 13

Системы координат

Нестационарное и стационарное температурное поле Для декартовой системы координат: Т = f(x, y, z, t) (1) где: § T –температура тела; § x, y, z -координаты точки; § t - время. Такое температурное поле называется нестационарным, т. е. соответствует неустановившемуся тепловому режиму теплопроводности. Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным: T = f(x, y, z) , ∂T/∂t = 0 (2) 15

Уравнения температурного поля Уравнение двухмерного температурного поля: § для нестационарного режима: T = f(x, y, t) ; ∂T/∂z = 0 (3) § для стационарного режима: T = f(x, y) , ∂T/∂z = 0; ∂T/∂t = 0 (4) Уравнение одномерного температурного поля: § для нестационарного режима: T = f(x, t) ; ∂T/∂y = ∂T/∂z = 0 ( 5) § для стационарного режима: T = f(x) ; ∂T/∂y = ∂T/∂z = 0; ∂T/∂t = 0 (6) 16

Изотермы Поверхность, во всех точках которой температура одинакова, называют изотермической. В плоскости пересечения тела эти поверхности оставляют следы в виде изотерм - линий одинаковой температуры. 17

Градиент температуры Градиентом температуры называют предел отношения изменения температуры ∆T к расстоянию между изотермами по нормали ∆n, когда ∆n стремится к нулю: |grad. T| = lim[∆T/∆n]∆n→ 0 = ∂T/∂n Градиент температуры – это вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры Т по этому направлению: grad. Т = (∂Т/∂n)·no (7) где: no – единичный вектор. 18

Тепловой поток § Количество теплоты, проходящее через изотермическую поверхность F в единицу времени называют тепловым потоком – Q, [Вт = Дж/с]. § Тепловой поток, проходящий через единицу площади называют плотностью теплового потока q = Q/F, [Вт/м 2] 19

Закон Фурье для теплопроводности Для твердого тела уравнение теплопроводности подчиняется закону Фурье: Тепловой поток, передаваемый теплопроводностью, пропорционален градиенту температуры и площади сечения, перпендикулярного направлению теплового потока: Q = -λ∙F∙ ∂Т/∂n (8) или q = -λ∙(∂Т/∂n)∙no = -λ∙grad. Т (9) где: q – вектор плотности теплового потока; 20

Коэффициент теплопроводности § Коэффициент теплопроводности является физическим параметром вещества, характеризующим способность тела проводить теплоту. § зависит от природы вещества, давления и температуры. Также на его величину влияет влажность вещества. Кирпич красный 0, 70 Серебро 420 § Коэффициенты теплопроводности некоторых Вода 0, 683 Медь 395 веществ , Вт/(м. Водород 273 К К), при 0, 172 Алюминий 207 Гелий 0, 143 Латунь (67 % Сu, 33 % Zn) 101 Кирпич диатомитовый Сталь 20 55 Кирпич пеношамотный Бетон сухой 0, 84 Воздух 0, 0244 0, 113 0, 100 21

Коэффициент температуропроводности а - физическое свойство вещества, от которого зависит скорость изменения температуры в нестационарных процессах теплопроводности. Чем больше а, тем быстрее тело охлаждается или нагревается Определяется по формуле: где - удельная теплоёмкость Значения а для некоторых веществ § Медь (Т= 273 К) § Воздух (Т= 273 К, р = 0, 101 МПа) § Сталь 20 (Т = 273 К) § Нержавеющая сталь Х 18 Н 9 Т § Вода (Т= 373 К, р = 0, 101 МПа) а 105 м 2/с 11, 6 1, 88 1, 16 0, 363 0, 0169 22

Дифференциальное уравнение температурного поля (уравнение Фурье) (без источников / стоков тепла) Дифференциальное уравнение, описывающее температурное поле в теле (в неподвижной среде) без внутренних источников (стоков) тепла, в любой момент времени в прямоугольной системе координат имеет вид: или через оператор Лапласа Это уравнение называется уравнением Фурье 23

Стационарная теплопроводность Для установившегося процесса передачи тепла (стационарный процесс) дифференциальное уравнение Фурье имеет вид: или через оператор Лапласа 24

Условия однозначности для уравнения теплопроводности Для решения этих дифференциальных уравнений Фурье должны быть заданы следующие дополнительные условия (условия однозначности): § 1) геометрические условия, характеризующие форму и размеры тела; § 2) физические условия, характеризующие физические свойства тела ( , С, …) и их зависимость от температуры; § 3) начальные условия, т. е. температурное поле в теле в начальный момент времени. В частности, температура тела в момент времени t = 0 может быть задана как постоянная величина для всех точек тела. 25 Для стационарной теплопроводности начальные условия не имеют смысла

Условия однозначности для уравнения теплопроводности (продолжение) § 4) Граничные условия, характеризующие воздействие окружающей среды на поверхность тела. Эти условия могут быть сформулированы различными способами: § а) граничные условия первого рода – задается температура в каждой точке поверхности тела в любой момент времени. T = f(x, y, z, τ) В простейшем случае температура может быть задана как постоянная величина во всех её точках и не меняться во времени; § б) граничные условия второго рода – задается плотность теплового потока в каждой точке поверхности 26 в любой момент времени q = f(x, y, z, τ)

Условия однозначности для уравнения теплопроводности (продолжение) в) граничные условия третьего рода линейные – задается температура окружающей среды Тж и закон теплообмена между поверхностью и окружающей средой (для конвективного теплообмена) в виде закона Ньютона Рихмана. Принято записывать линейные граничные условия третьего рода в форме уравнения где закона сохранения энергии для - коэффициент теплоотдачи, Вт/(м 2 К). поверхности тела 27

Условия однозначности для уравнения теплопроводности (продолжение) § г) граничные условия третьего рода нелинейные – задается температура окружающей среды и закон теплообмена между поверхностью и окружающей средой осуществляющийся излучением Это уравнение Стефана-Больцмана, где Спр – приведённый коэффициент излучения [Вт/(м 2 К 4] В общем случае при граничных условиях третьего рода температура Тж и коэффициент теплоотдачи могут меняться во времени, а также при переходе от одной точки 28 поверхности к другой.

Способы задания граничных условий Граничные условия первого рода Распределение температуры на поверхности тела Граничные условия второго рода Распределение плотности теплового потока на поверхности тела Граничные Условия теплообмена условия поверхности тела с третьего рода окружающей средой: – линейные - конвективный; - нелинейные - излучением. T = f(x, y, z, τ) q = α(Тж– Тп) = = -λ∙ ∂Т/∂n│n→ 0 29

Стационарная теплопроводность и теплопередача в твёрдых телах 30

Плоская стенка с граничными условиями 1 -го рода § Однослойная стенка с коэфф. теплопроводности λ = const. § Плоская стенка, толщина (по оси х) которой существенно меньше её протяженности по y и z. § Тепловой поток можно принять одномерным в направлении x. По уравнению Фурье имеем: Двойное интегрирование приводит к функции, которая показывает, что по толщине температура изменяется прямолинейно. 31 где С 1 и С 2 - константы интегрирования

Плоская стенка с граничными условиями 1 -го рода (продолжение) При граничных условиях первого рода заданы температуры на границах стенки: § При x = 0 § T = Tn 1 ; § при x = § T = Tn 2 Получаем константы интегрирования § С 2 = Т n 1, § C 1 = (Tn 2 – Tn 1)/ § Тогда температура тела в точке с координатой х: 32

Плоская стенка с граничными условиями 1 -го рода или с другим направление теплового потока 33 По толщине стенки температура изменяется прямолинейно

Плотность теплового потока для плоской стенки с граничными условиями 1 рода § Для однородной плоской стенки толщиной , коэффициент теплопроводности которой равен [Вт/(м К)], и не зависит от температуры, плотность теплового потока q определяется по формуле: Обозначим R - термическое сопротивление Тогда получаем: 34

Многослойная стенка при l = const с граничными условиями 1 -го рода Стенка состоит из последовательно расположенных слоев толщиной i и теплопроводности i общая толщина стенки существенно меньше остальных размеров (y и z). Так как тепловой поток постоянен, то: 35

Плотность тепловых потоков многослойную стенку при l = const с граничными условиями 1 -го рода Плотности тепловых потоков через каждый слой стенки: § q = λ 1/δ 1∙(Тn 1 – Тn 2) § q = λ 2/δ 2∙(Тn 2 – Тn 3) § q = λ 3/δ 3∙(Тn 3 – Тn 4). . . …………. Складывая левые и правые части получаем: 36
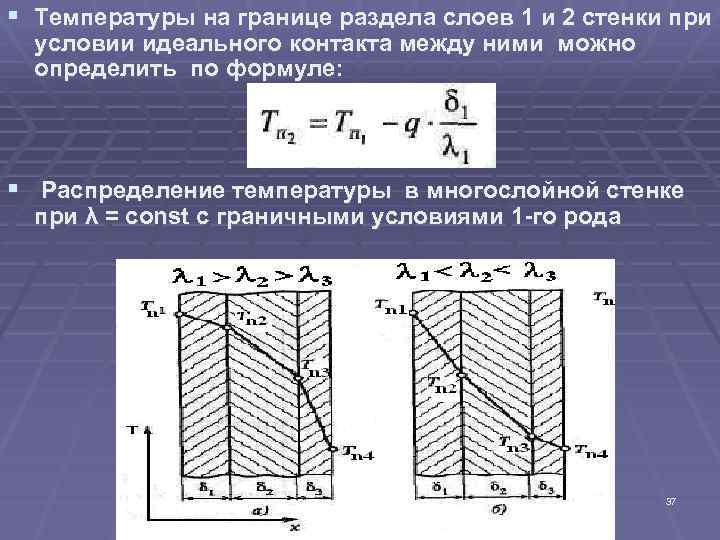
§ Температуры на границе раздела слоев 1 и 2 стенки при условии идеального контакта между ними можно определить по формуле: § Распределение температуры в многослойной стенке при λ = const с граничными условиями 1 -го рода 37

Плоская стенка с граничными условиями 3 -го рода Практически важным является процесс, в котором известными считаются величины, входящие в граничные условия третьего рода: § температуры жидкостей Тж 1 и Тж 2 с двух сторон стенки; § коэффициенты теплоотдачи со стороны первой a 1 и со стороны второй a 2 жидкостей. 38

Закон Ньютона-Рихмана Процесс теплообмена между поверхностью тела и средой описывается законом Ньютона-Рихмана, который гласит, что количество теплоты, передаваемой конвективным теплообменом прямо пропорционально разности температур поверхности тела (Тс) и окружающей среды (Тж): Q = α(Тс - Тж)·F (1) или q = α(Тс - Тж) (2) где: α - коэффициент теплоотдачи [Вт/(м 2 К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. 39

Теплопередача и три Процесс переноса теплоты от одной жидкости термических сопротивления к другой через разделяющую их стенку называется теплопередачей. Процессу теплопередачи препятствуют три термических сопротивления: § внутреннее R = d/ (для многослойной стенки оно равно сумме термических сопротивлений слоев): 40
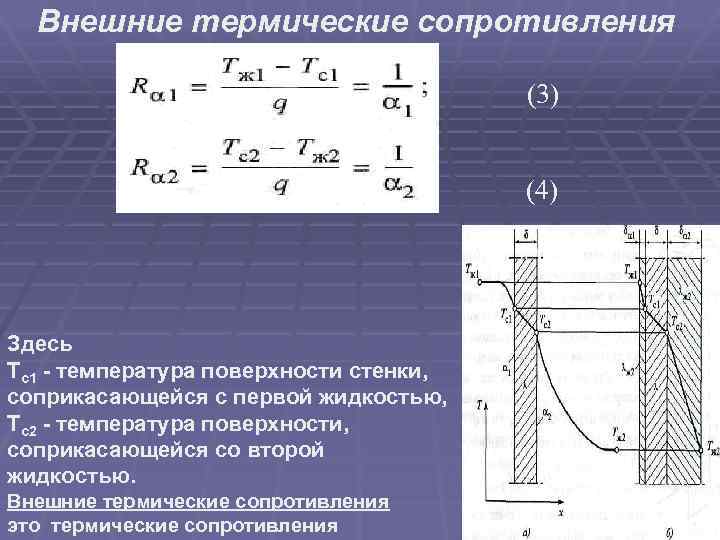
Внешние термические сопротивления (3) (4) Здесь Тс1 - температура поверхности стенки, соприкасающейся с первой жидкостью, Тс2 - температура поверхности, соприкасающейся со второй жидкостью. Внешние термические сопротивления это термические сопротивления 41

§ Имеем систему трех уравнений с неизвестными Тс1, Тс2 и q. § Если эти три уравнения сложить, то неизвестные Тс1 и Тс2 сокращаются. § В результате получим уравнение плотности теплового потока: (5) 42

Коэффициент теплопередачи § Отношение плотности теплового потока q к температурному напору T = Тж 1 - Tж 2 называют коэффициентом теплопередачи k [Вт/(м К)]: k = q / T Из (5) следует, что для однослойной плоской стенки коэффициент теплопередачи: Для однослойной плоской стенки: 43

Коэффициент теплопередачи § Коэффициент теплопередачи k характеризует интенсивность процесса теплопередачи. § В соответствие с формулой k = q / T он численно равен плотности теплового потока, передаваемого через стенку при температурном напоре, равном единице. § Это величина, обратная сумме всех термических сопротивлений § Если одно из сопротивлений значительно больше всех остальных, то практически оно одно и будет определять 44 значение коэффициента теплопередачи.
лек 8 Основы и матем. описание теплообм БАФ.ppt