Теплотехника Конспект лекций ч 1 Техническая термодинамика 1

Теплотехника Конспект лекций ч. 1 Техническая термодинамика 1

• Теплотехника – общетехническая дисциплина, изучающая методы получения, преобразования, передачи и использования теплоты, а также принцип действия и конструктивные особенности тепло и парогенераторов, тепловых машин, аппаратов и устройств. Теоретические основы теплотехники – I. термодинамика (техническая) II. теория тепломассообмена (теплопередача) 2

I. ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА • изучает закономерности взаимного превращения тепловой и механической энергии и свойства тел, участвующих в этих превращениях. • На ее основе осуществляют расчет и проектирование всех тепловых двигателей: • паровых и газовых турбин, • реактивных и ракетных двигателей, • двигателей внутреннего сгорания, • всевозможного технологического оборудования – компрессоров, сушильных и холодильных установок, систем кондиционирования и вентиляции…. 3

• Термодинамическая система – совокупность материальных тел, находящихся в механическом и тепловом взаимодействиях друг с другом и с окружающими систему внешними телами ( «внешней средой» ). • Свойства каждой системы и происходящие в ней процессы характеризуются величинами, называемыми термодинамическими параметрами. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ (ТДП) ТДП состояния – физические величины, однозначно характеризующие состояние термодинамической системы и не зависящие от предистории системы (например, температура Т, давление Р, объем V, внутренняя энергия U, энтальпия I (H), энтропия S); ТДП процесса (работа L, теплота Q, теплоемкость C), значения которых зависят от процесса перехода из начального состояния системы в конечное. 4

1 АБСОЛЮТНОЕ ДАВЛЕНИЕ • Обозначение: Р • Размерность: [Па] (паскаль) 1 Па = 1 Н/м 2 1 к. Па = 103 Па, 1 МПа = 106 Па Блез Паска ль (фр. Blaise Pascal ), 1623 1662 Французский математик, физик, литератор, философ. Классик фр. литературы, один из основателей математич. анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики. 5

Соотношение между единицами измерения давления: • 1 мм рт. ст. (миллиметр ртутного столба) = 133, 3 Па • • • 1 бар = 105 Па =0, 1 МПа = 750 мм рт. ст. ; 1 ат (техническая) = 735 мм рт. ст. ; 1 атм (физическая) = 760 мм рт. ст. ; 1 мм вод. ст. (миллиметр водяного столба) = 9, 8 Па; 1 кг/см 2 = 1 ат = 9, 8067 104 Па. • 1 бар ≈ 1 атм ≈ 1 кг/см 2 ≈ 105 Па = 100 к. Па 6

ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ: • Барометры – для измерения атмосферного (барометрического) давления В = Ратм= Рбар; • Манометры – для измерения давления выше атмосферного (избыточного) Рман = Ризб; • Вакуумметры – для давления ниже атмосферного Рвак = h – разрежение. Термодинамическим параметром является давление абсолютное Р, которое приборами не измеряется, а требует расчета: • P = Рабс = В + Рман = Ратм + Ризб • P = Рабс = В – Рвак = В – h 7

2 АБСОЛЮТНАЯ ТЕМПЕРАТУРА • Обозначение: Т • Размерность: [К] (кельвин, до 1968 г. градус Кельвина) Температурные шкалы и единицы измерения температуры: наиболее распространенная в Европе – шкала Цельсия: 0 о. С – температура замерзания воды при атмосф. давлении, 100 о. С – температура кипения воды при атмосферном давлении. T [K] = t [о. С] + 273, 15 T [K] = t [о. С] 8

Уи льям То мсон, лорд Ке львин (1892) (William Thomson), 1824 -1907 Британский физик. Место работы – Университет Глазго. «лорд Кельвин Ларгский из Айршира» Андерс Цельсий (Anders Celsius) 1701 -1744 Шведский астроном, геолог и метеоролог Место работы Уппсальский университет 9

• В Северной Америке используется шкала Фаренгейта Предложена немецким физиком Даниелем Габриелем Фаренгейтом (1686 1736) в 1724 году t [о. С] = 5/9 (t [о. F] – 32), t [о. F] = 9/5 t [о. С] + 32 0° F — температура замерзания смеси воды, льда и нашатыря (1: 1: 1) Фаренгейт принял чрезвычайно низкую температуру зимы 1709 г. в Данциге за нуль для своей шкалы; 96° F — температура тела здорового человека; 32° F — температура таяния льда; 1 °F — 1/180 разности т р кипения воды и таяния льда при атмосферном давлении 10

11

• Самая высокая температура, созданная человеком, ~ 10 трлн. К (достигнута в 2010 г. на Большом Андронном Коллайдере при столкновении ионов свинца, ускоренных до околосветовых скоростей). • Самая высокая теоретически возможная температура — планковская температура — 1. 41679(11)· 1032 K. • Поверхность Солнца — ок. 6000 K. • Самая низкая температура, созданная человеком (1995 г. ), получена в США при охлаждении атомов рубидия — выше абсолютного нуля на 1/170 млрд. долю K (5, 9· 10− 12 K). • Рекордная низкая температура на поверхности земли − 89. 2° С (на советской внутриконтинентальной научной станции Восток, Антарктида, 21 июля 1983 г. ) • Рекордно высокая температура на поверхности земли + 56, 7 ˚C (на ранчо Гринленд в долине Смерти (штат Калифорния, США) 10 июля 1913 года ). 12

ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ: • Термометры жидкостные, металлические, газовые • Термопары 13

ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ: • Пирометр прибор для бесконтактного измерения т ры тел. Принцип действия: измерение мощности теплового излучения объекта преимущественно в диапазонах инфракрасного излучения и видимого света. • Дилатомер • Конус Зегера (пироскоп) 14

3 УДЕЛЬНЫЙ ОБЪЕМ Удельный объем – объем единицы массы вещества (1 кг). • Обозначение: v = V/m. • Размерность: [м 3/кг]. где V [м 3] – объем тела массой m [кг]. r = 1/v , [кг/м 3] плотность – величина, обратная удельному объему. 15

н. ф. у. «нормальные физические условия» Ро = (760 мм рт. ст. ) = 101, 325 к. Па @ 0, 1 МПа = 105 Па; То = (0 о. С) = 273, 15 К 16

УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНЫХ ГАЗОВ – уравнение Менделеева Клапейрона Бенуа Поль Эми ль Клапейро н (Clapeyron, Benoît Paul) 1799 1864, французский физик и инженер. В 1820 1830 профессор Петербургского института путей сообщения. Заведовал кафедрами механики и химии. 1830 – чл. корр. Петербургской АН Внесен в список ученых Франции на 1 этаже Эйфелевой башни. Дми трий Ива нович Менделе ев (1834 -1907) русский ученый-энциклопедист: химик, физикохимик, физик, метролог, экономист, технолог, геолог, метеоролог, педагог, воздухоплаватель, приборостроитель 17

УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНЫХ ГАЗОВ – уравнение Менделеева Клапейрона • для 1 кг газа: Рv = Rг. T • для m кг газа: РV = m. Rг. T , где Rг = R/m – газовая постоянная (удельная) данного газа, [Дж/ (кг. К)], • R = 8, 314 Дж/(моль. К) – универсальная газовая постоянная (для 1 моля идеального газа), • m – молекулярная масса данного газа [кг/моль], • для 1 моля газа Pvm= 8, 314 T , где vm – объем моля газа. • для m кг газа: PV = m. RT/m. 18

МОЛЕКУЛЯРНАЯ МАССА, m: • • Кислород О 2 32 Азот N 2 28 Воздух (78% ОБ. N 2 +21% О 2) 29 Углекислый газ CО 2 44 Водород H 2 2 Водяной пар H 2 O 18 Метан CH 4 16 г/моль • В расчетах не забыть х10 3 кг/моль 19

Задачи из к/о № 1 • Определить плотность углекислого газа при н. ф. у. • Какой газ находится в сосуде, если его плотность Х, Х кг/м 3 при давлении Х, Х МПа и температуре ХХ 0 С? • Определить плотность углекислого газа, находящегося в сосуде при температуре ХХ 0 С, если показание манометра Х, Х бар, а барометра ХХ, Х к. Па. • Каково давление в сосуде, если разрежение составляет ХХ к. Па. Барометрическое давление 760 мм рт. ст. • Какова масса воздуха в сосуде объемом 120 м 3 , находящегося при нормальных физических условиях. • Как изменится давление в сосуде постоянного объема, если температура газа увеличится с 25 0 С до 75 0 С? 20

4 ТЕПЛОЕМКОСТЬ Теплоемкость – количество теплоты, которое необходимо сообщить телу (газу), чтобы повысить температуру какой-либо его количественной единицы (кг, м 3, моль) на 1 градус. Удельная теплоемкость, отнесенная • к 1 кг – массовая С Дж/(кг. К), • к 1 м 3 – объемная С‘ Дж/(м 3 К) , • к 1 молю – мольная m. С Дж/(моль. К), где m молекулярная масса вещества, [кг/кмоль], (для воздуха: m = 29 кг/кмоль), 22, 4 м 3/кмоль – объем 1 моля газа при н. ф. у. (Ро = 101, 3 к. Па, То = 273, 15 К). 21

Теплоемкость определяется: • истинная (при данной температуре) • средняя (в интервале температур от Т 1 до Т 2) Численно теплоемкость изменяется в пределах от –∞ до +∞ ! Теплоемкость может иметь отрицательное значение ! для определенного типа процессов (см. ниже). Величина dq/d. T не является производной, потому что dq не изменение теплоты, а ее малое количество. Для того, чтобы подчеркнуть это, обычно пишут δq/d. T. Теплоемкость в таком определении не является функцией состояния, так как теплота характеризует не состояние, а процесс передачи энергии. 22

• Теплоемкость – функция процесса. Одно и то же рабочее тело в зависимости от процесса требует для своего нагревания на 1 градус различного количества теплоты. Наиболее часто используются: • изобарная теплоемкость Ср (при подводе или отводе теплоты при постоянном давлении P=const); • изохорная теплоемкость Сv (при подводе или отводе теплоты при постоянном объеме V=const). 23

• Для идеальных газов: – уравнение Майера где Rг = R/m – газовая постоянная для данного газа, [Дж/(кг. К)], R = 8, 314 – универсальная газовая постоянная, [Дж/(моль. К)]. • Для мольных теплоемкостей: m. Ср – m. Сv = R [Дж/моль. К], или m. Ср = m. Сv + 2 [ккал/кмоль. К]. Кроме того: , где k – показатель адиабаты. Для процессов с постоянной теплоемкостью: • k = 1, 67 (для одноатомных газов), • k = 1, 4 (для двухатомных газов), • k = 1, 3 (для трех и многоатомных газов). 24

I ЗАКОН ТЕРМОДИНАМИКИ d. Q = d. U + d. L 25

I ЗАКОН ТЕРМОДИНАМИКИ d. Q = d. U + d. L – теплота, сообщенная системе, идет на приращение ее внутренней энергии U и на совершение газом внешней работы L для 1 кг рабочего тела: dq в интегральной форме : = du + dl, q = u +l 26

5 ВНУТРЕННЯЯ ЭНЕРГИЯ u = U/m Обозначение: – удельная внутренняя энергия – – внутренняя энергия единицы массы вещества Размерность: [Дж/кг] 27

5 ВНУТРЕННЯЯ ЭНЕРГИЯ Внутренняя энергия – параметр состояния Для всех процессов изменение внутренней энергии: u =сv T (в интегр. форме) du =сvd. T (в диф. форме) 28

6 РАБОТА (изменения объема). l = L/m Обозначение: – удельная работа единицы массы вещества Размерность: [Дж/кг] Работа изменения объема закрытой системы равна произведению давления на приращение объема: dl = Pdv 29

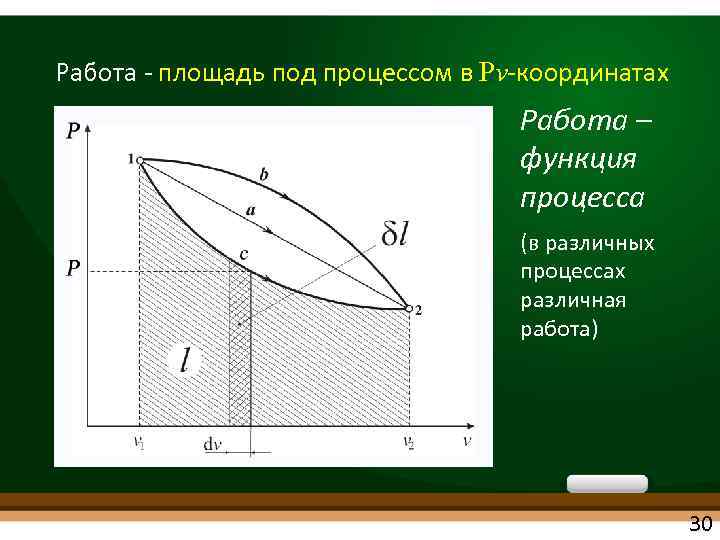Работа площадь под процессом в Pv координатах Работа – функция процесса (в различных процессах различная работа) 30

7 ТЕПЛОТА . q = Q/m Обозначение: – удельная теплота единицы массы вещества Размерность: [Дж/кг] Теплота и работа – формы передачи энергии. Теплота – микрофизическая форма передачи энергии. Работа – макрофизическая форма передачи энергии. Теплота – функция процесса. Значение данного параметра будет зависеть от процесса перехода из начального состояния в конечное. 31

8 ЭНТАЛЬПИЯ Введена Гиббсом в XIX веке. i = I/m Обозначение: – удельная энтальпия – отношение энтальпии тела I к его массе m Возможен другой вариант обозначения: h (H) Размерность: [Дж/кг] 32

8 ЭНТАЛЬПИЯ Введена Гиббсом в XIX веке. Удельная энтальпия i = u + Pv Энтальпия – сумма внутренней энергии тела U и произведения давления P на объем V. Энтальпию можно трактовать как энергию расширенной системы. Энтальпия – это та энергия, которая доступна для преобразования в теплоту при определенных температуре и давлении. 33

Энтальпия – функция состояния и, следовательно, изменение энтальпии в термодинамическом процессе не зависит от характера процесса, а определяется только начальным и конечным состоянием тела. Для всех процессов изменение энтальпии: i =сp T di =сpd. T 34

I ЗАКОН ТЕРМОДИНАМИКИ В ЗАПИСИ ЧЕРЕЗ ЭНТАЛЬПИЮ (вторая форма записи I закона термодинамики) dq = du + Pdv С учетом i = u + Pv u = i – Pv du = di – (vd. P+Pdv) dq = du + dl = (di – vd. P – Pdv)+Pdv dq = di – vd. P 35

ЧВС № 1 В изобарном процессе Р = const и d. P = 0, dq = di – vd. P = di = сpd. T при qp = i 2 – i 1 Теплота, подведенная к системе при постоянном давлении, идет только на изменение энтальпии данной системы 36

9 ЭНТРОПИЯ Введена Клаузиусом в 1865 г. . s = S/m Обозначение: – удельная энтропия – отношение энтропии тела S к его массе m Размерность: [Дж/(кг. К)] 37

• Можно показать, что энтропия – функция состояния рабочего тела, не зависит от процесса перехода из начального в конечное состояние, и ds является полным дифференциалом. • Изменение энтропии в каком либо процессе: где сn – теплоемкость данного процесса 38

• С учетом I закона термодинамики и уравнения Клапейрона изменение энтропии равно: В процессах при постоянном объеме V = const: В процессах при постоянном давлении Р = const: 39

• Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов Тs-диаграмму Т. к. dq=Tds Теплота – площадь под процессом в Ts-диаграмме 40

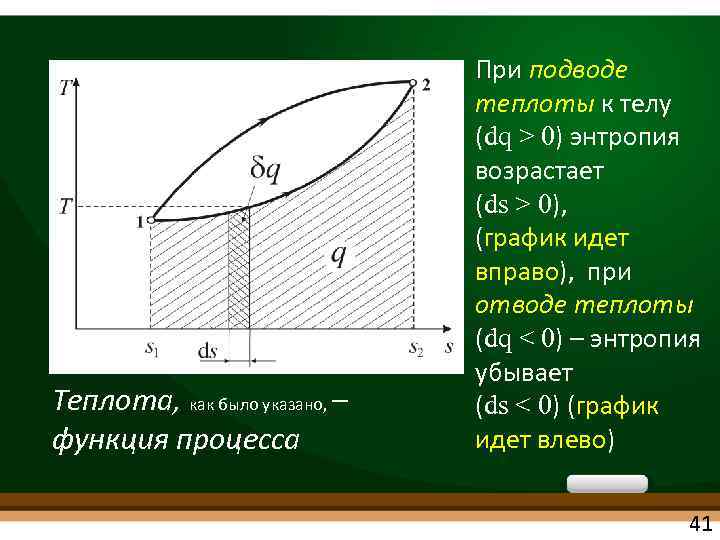Теплота, как было указано, – функция процесса При подводе теплоты к телу (dq > 0) энтропия возрастает (ds > 0), (график идет вправо), при отводе теплоты (dq < 0) – энтропия убывает (ds < 0) (график идет влево) 41

III ЗАКОН ТЕРМОДИНАМИКИ (тепловая теорема Нернста) • 1906 г. , Вальтер Нернст при температуре, стремящейся к абсолютному нулю 0 К, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической решеткой, стремится к 0 So 0 при Т 0 42

• III закон позволяет рассчитать абсолютное значение энтропии, в отличие от внутренней энергии или энтальпии, которые отсчитываются от произвольного уровня • «Энтропия – мера порядка (хаоса)» S = 0 100% «порядок» • При увеличении энтропии возрастает разупорядоченность, степень хаоса Smax 100% «хаос» 43

II ЗАКОН ТЕРМОДИНАМИКИ • указывает направление теплового потока • устанавливает максимально возможный предел превращения теплоты в работу в тепловых машинах Аналитически II закон термодинамики выражается зависимостью 44

• Формулировки второго закона термодинамики: • Вечный двигатель второго рода невозможен (под вечным двигателем второго рода понимается машина, которая могла бы превращать всю подводимую к ней теплоту в работу. Такая машина имела бы КПД = 100 %) – постулат Оствальда. • Невозможна периодически действующая тепловая машина, единственным результатом действия которой было бы получение работы за счет отнятия теплоты от некоторого источника (постулат Томсона). • Теплота не может самопроизвольно (без компенсации) переходить от тел с более низкой температурой к телам с более высокой температурой (постулат Клаузиуса). • Всякое изменение состояния системы происходит самопроизвольно только в том направлении, при котором может иметь место переход частей системы от менее вероятного к более вероятному распределению (постулат Больцмана). • Сумма изменений энтропии системы и внешней среды не может убывать и др. формулировки 45

Резюмируя первый и второй законы термодинамики, Клаузиус констатировал: • Энергия Вселенной постоянна. • Энтропия Вселенной стремится к максимуму. • Максимуму энтропии соответствует устойчивое равновесие системы. • Увеличение энтропии отличает будущее от прошлого, поэтому существует стрела времени: «Энтропия – стрела времени» 46

Принцип возрастания энтропии • Самопроизвольные (неравновесные) процессы в изолированной системе всегда приводят к увеличению энтропии наиболее общая формулировка второго начала термодинамики для неравновесных процессов «Тепловая смерть» Вселенной можно предвидеть то время, когда Вселенная окажется в состоянии с максимальной энтропией. Тогда все тела приобретут одинаковую температуру, тепловая энергия не сможет больше превращаться в работу, наступит «тепловая смерть» Вселенной 47

• Решение проблемы – не считать Вселенную изолированной системой 48

• ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ 49

ИЗОХОРНЫЙ ПРОЦЕСС • dv = 0 или v = const • Из уравнения состояния идеального газа Рv = RT при v = const получаем P/T = Rг/v = const • При постоянном объеме давление газа изменяется прямо пропорционально абсолютным температурам (закон Шарля): P 1/P 2= T 1/T 2 50

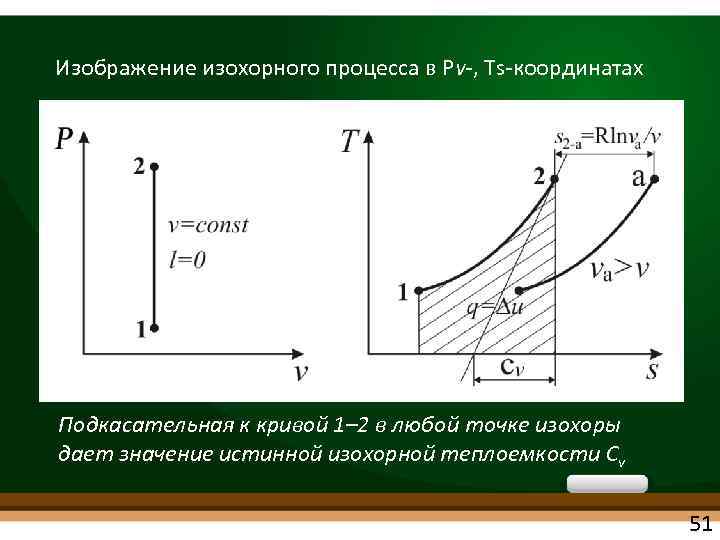Изображение изохорного процесса в Рv , Ts координатах Подкасательная к кривой 1– 2 в любой точке изохоры дает значение истинной изохорной теплоемкости Сv 51

qv = u = cv T = cv(T 2 –Т 1) u = cv T i = cp T u = Cv T 52

ИЗОБАРНЫЙ ПРОЦЕСС • d. P = 0 или P = const • Из уравнения состояния идеального газа Рv = RT при P = const получаем v/T = Rг/P = const • При постоянном давлении объемы газа изменяются прямо пропорционально абсолютным температурам (закон Гей-Люссака): v 1/v 2= T 1/T 2 53

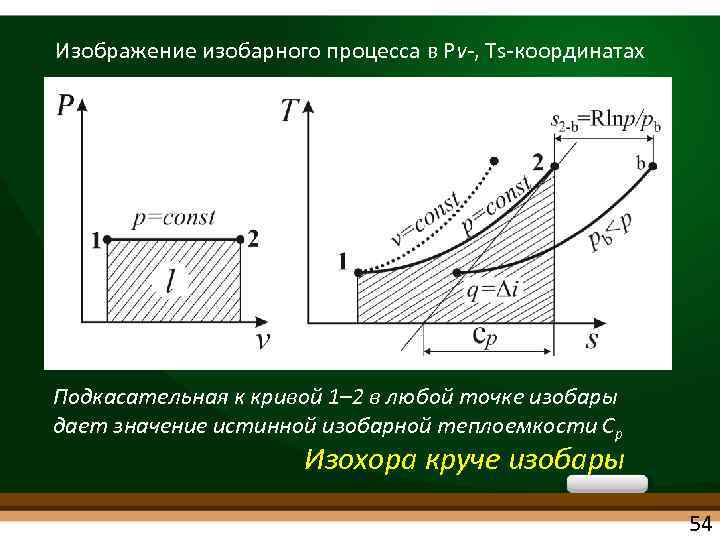Изображение изобарного процесса в Рv , Ts координатах Подкасательная к кривой 1– 2 в любой точке изобары дает значение истинной изобарной теплоемкости Ср Изохора круче изобары 54

qp = i = cp T = cp(T 2 –Т 1) l= P v=P(v 2 – v 1) u = cv T i = cp T u = Cv T 55

ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС • d. Т = 0 или Т = const • Из уравнения состояния идеального газа Рv = RT при Т = const получаем Рv = const - уравнение изотермы • При постоянной температуре абсолютное давление газа обратно пропорционально объему (закон Бойля-Мариотта): P 1/P 2= v 2/v 1 56

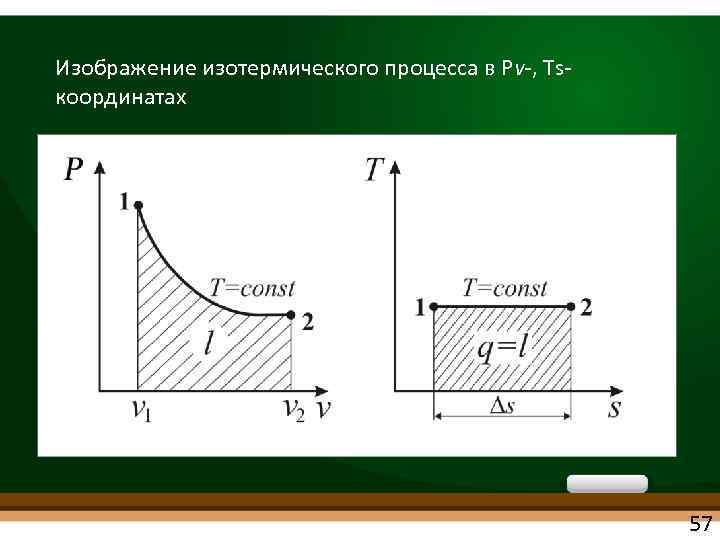Изображение изотермического процесса в Рv , Ts координатах 57

• u = cv T = 0 i = cp T= 0 u = Cv T 58

АДИАБАТНЫЙ ПРОЦЕСС • без теплообмена с окружающей средой • dq = 0 q=0 • Т. к. ds = dq/T = 0 S = const • Процесс изоэнтропийный k Рv = const s = 0 - уравнение адиабаты Tv k-1 = const, где k – показатель адиабаты k =1, 4 (для 2 х атомных газов) 59

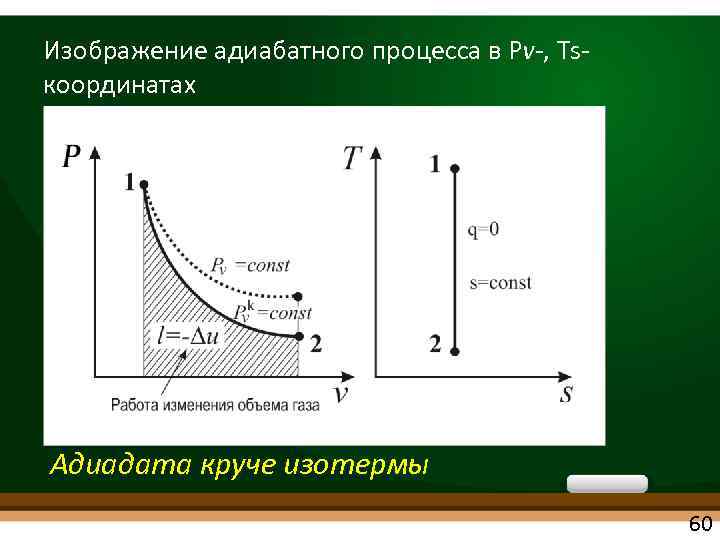Изображение адиабатного процесса в Рv , Ts координатах Адиадата круче изотермы 60

q=0 l = - u = cv(T 1 - T 2) u = сv T = cv(T 2 - T 1) i = сp T s = 0 u = Cv T 61

ПОЛИТРОПНЫЙ ПРОЦЕСС • 62

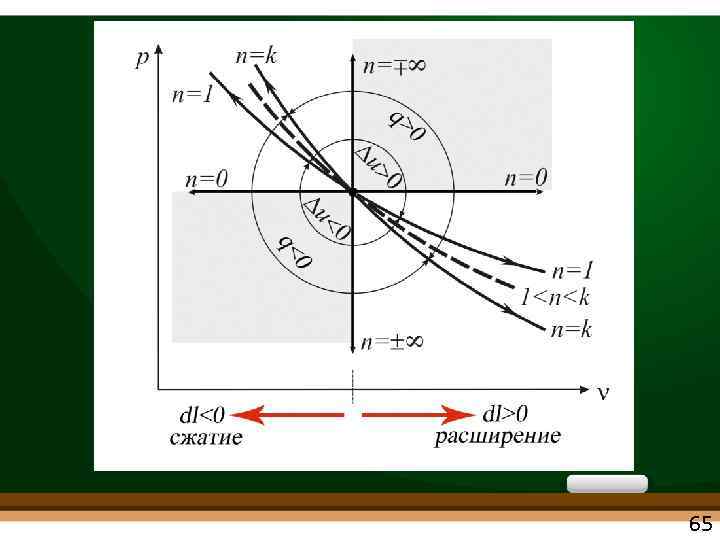
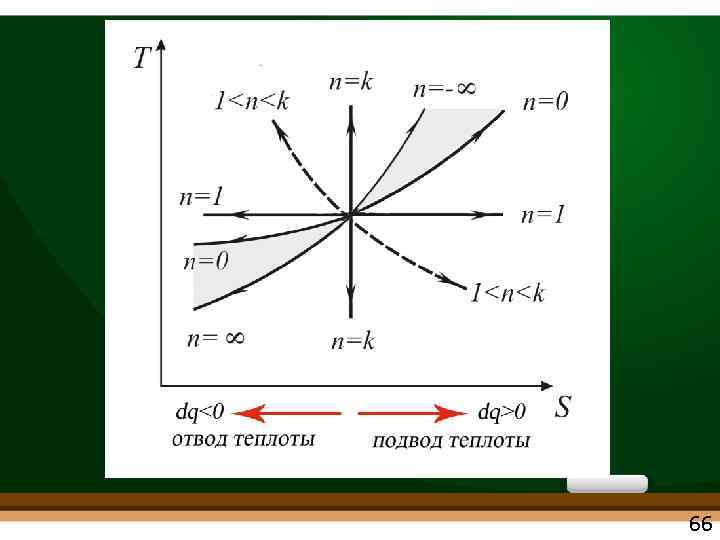
Изохорный, изобарный, изотермический, адиабатный процессы являются частными случаями политропного процесса Рvn = const • • изохорный n = ± ∞ изобарный n = 0 изотермический n = 1 адиабатный n = k сv сp с=q/ t= ± ∞ с=q/ t=0 63

ЧВС № 2 • 64

65

66

РЕАЛЬНЫЕ ГАЗЫ. ВОДЯНОЙ ПАР В отличие от идеальных необходимо учитывать: ❶силы межмолекулярных взаимодействий ❷собственный объем молекул ❸ассоциацию (диссоциацию) молекул Рv ≠ RT Необходимы поправки в уравнение состояния (Бертло, Клаузиус, Ван-дер-Ваальс и др. ) 67

Уравнение Ван-дер-Ваальса (P + a/v 2) (v – b) = Rг. T Учит. сил взаимод. Учит. влияние объема (не учит. асс/диссоциацию) Наиболее точно - уравнение Вукаловича-Новикова P v = Rг. T(1 – А/v – В/v 2) « таблицы насыщения водяного пара » « i-s-диаграмма водяного пара » 68

Получение пара • • Испарение (с поверхности) Кипение (во всем объеме) Сублимация (из тв. фазы в газообр. ) – сухой лед Декомпрессия (при резком сбросе давления парообразование начинается в объеме жидкости, при опр. усл. – взрывооп. хар р) – водолазы Наиболее часто – кипение – получение пара из жидкости при пост. Р 69

Диаграммы водяного пара • Рассмотрим процесс получения пара в различных координатах (Pv-, Ts-, is-) 70

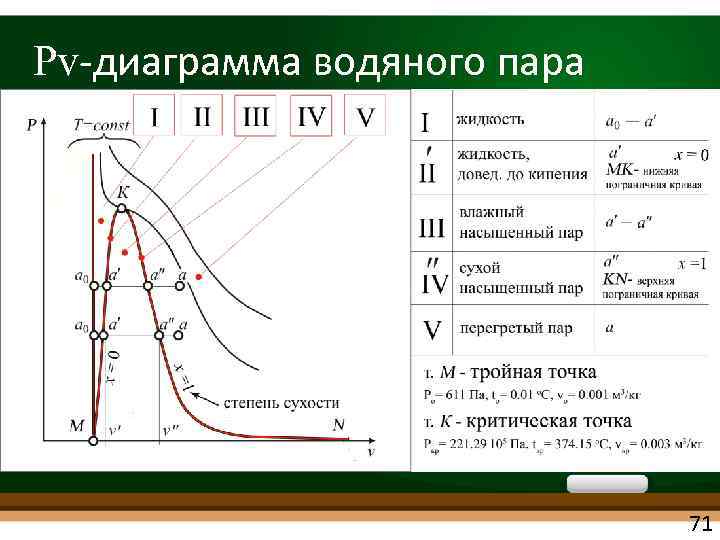Pv диаграмма водяного пара 71

• Процесс парообразования является изобарно изотермическим: P=const и T=const • Tемпература кипения (насыщения) Tн однозначно определяется давлением Tн= f(Pн) и Pн= f(Tн) • Насыщенным называется пар, находящийся в термическом и динамическом равновесии с жидкостью, из которой он образуется. • Насыщенный пар, в котором отсутствуют взвешенные частицы жидкой фазы сухой насыщенный пар • Двухфазная смесь пар со взвешенными в нем капельками жидкости влажный насыщенный пар 72

• Перегретым называется пар, температура которого превышает температуру насыщенного пара того же давления • Чем выше температура перегрева (при данном давлении), тем ближе пар по своим свойствам к идеальному газу • Критическое состояние вещества впервые было открыто Д. И. Менделеевым в 1861 г. Критическую температуру Менделеев назвал абсолютной температурой кипения, при которой поверхностное натяжение в жидкости становится равным нулю, т. е. исчезает различие между жидкостью и парообразным состоянием вещества (насыщенным паром) • В критической точке различия между жидкостью и паром исчезают. Свойства вещества в сверхкритическом состоянии промежуточные между его свойствами в газовой и жидкой фазе. 73

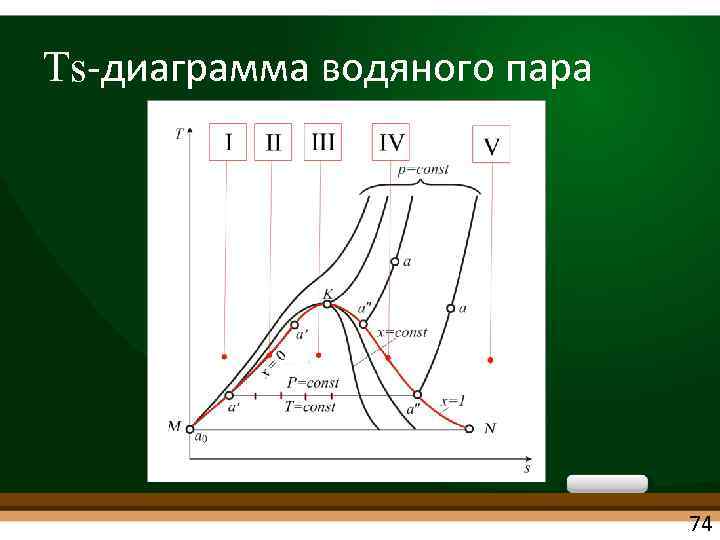Ts диаграмма водяного пара 74

H(i)s диаграмма водяного пара • Немецкий теплофизик Рихард Молье. 1904 г. • При P=const : qp = i • Теплота q – отрезок вертикальной прямой i в i-s-координатах – удобно! • ЧВС 3 – адиабатный процесс (работа пара в турбине) – – вертикаль в i-s-координатах – удобно! 75

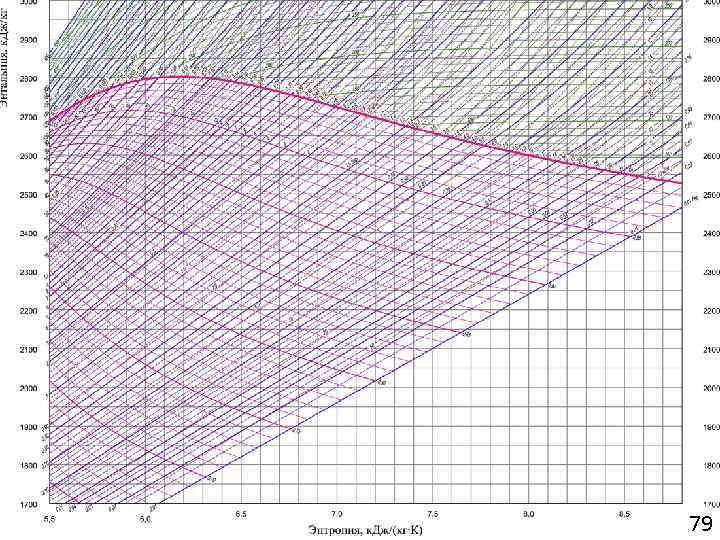
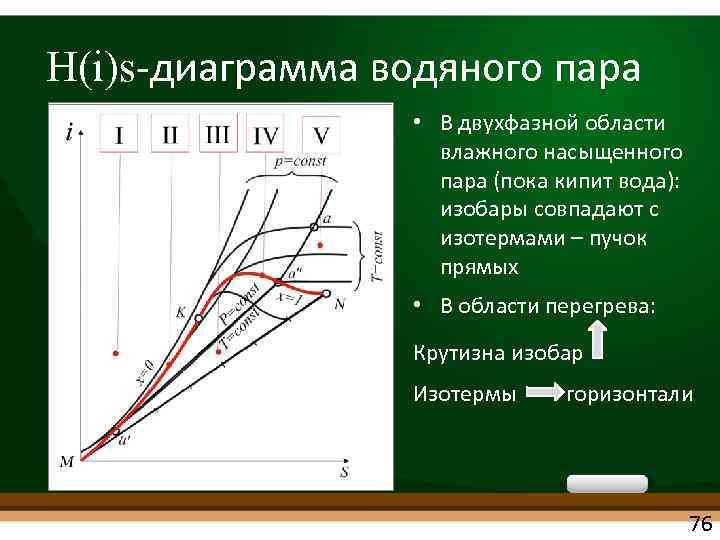H(i)s диаграмма водяного пара • В двухфазной области влажного насыщенного пара (пока кипит вода): изобары совпадают с изотермами – пучок прямых • В области перегрева: Крутизна изобар Изотермы горизонтали 76

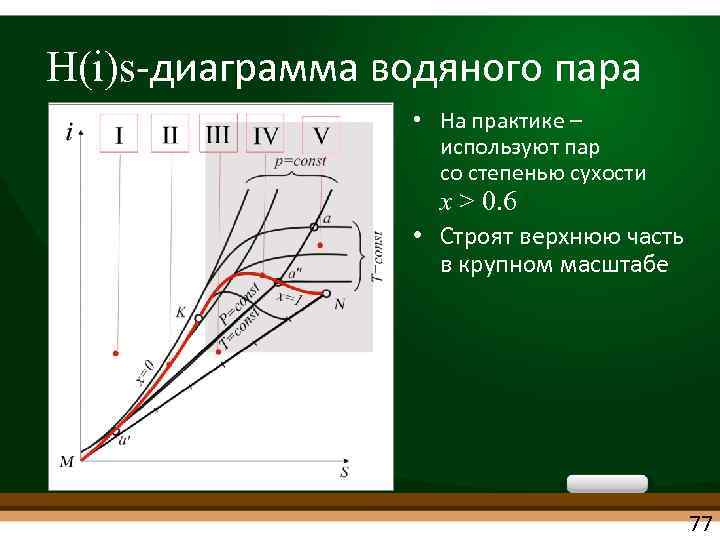H(i)s диаграмма водяного пара • На практике – используют пар со степенью сухости x > 0. 6 • Строят верхнюю часть в крупном масштабе 77

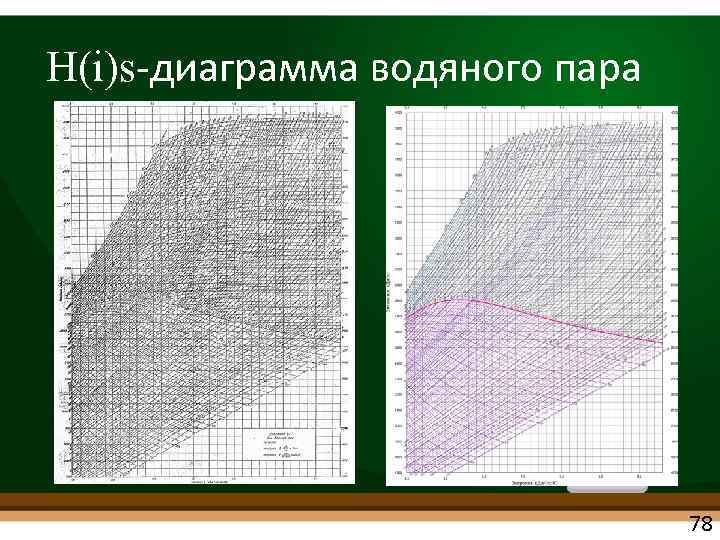H(i)s диаграмма водяного пара 78

79

Влажный воздух – смесь сухого воздуха и водяного пара. • знание свойств влажного воздуха необходимо для расчета: систем вентиляции, кондиционирования, процессов сушки, увлажнения, горения и др. Влажный воздух: • насыщенный – сухой воздух + сухой насыщенный пар; • пересыщенный – сухой воздух + влажный насыщенный пар; • ненасыщенный – сухой воздух + перегретый пар. (!) 80

• 81

Основные характеристики влажного воздуха • Абсолютная влажность rп , [кг/м 3] – концентрация водяного пара – количество водяных паров, содержащихся в 1 м 3 влажного воздуха, (плотность пара при его парциальном давлении и температуре воздуха). • Относительная влажность ϕ, [%] – отношение фактической концентрации пара во влажном воздухе к максимально возможной. 82

• ϕ = 0 – сухой воздух • ϕ = 100 % – насыщенный влажный воздух • Влагосодержание d, [г/кг сухого воздуха] – отношение массы пара к массе сухого воздуха во влажном воздухе • Относительная влажность и влагосодержание влажного воздуха могут быть определены с помощью психрометра. 83

• Психрометр состоит из двух термометров – сухого и мокрого. Шарик ртути мокрого термометра покрыт слоем ткани, непрерывно смачиваемой водой. 84

• 85

H(i) d диаграмма влажного воздуха • Предложена Л. К. Рамзиным (1918 г. ) • Упрощает решение ряда практических задач в области кондиционирования, вентиляции, отопления, сушки материалов и др. • построена для среднегодового барометрического давления в центральных районах России Р = В = 99. 3 к. Па (745 мм рт. ст. ) 86

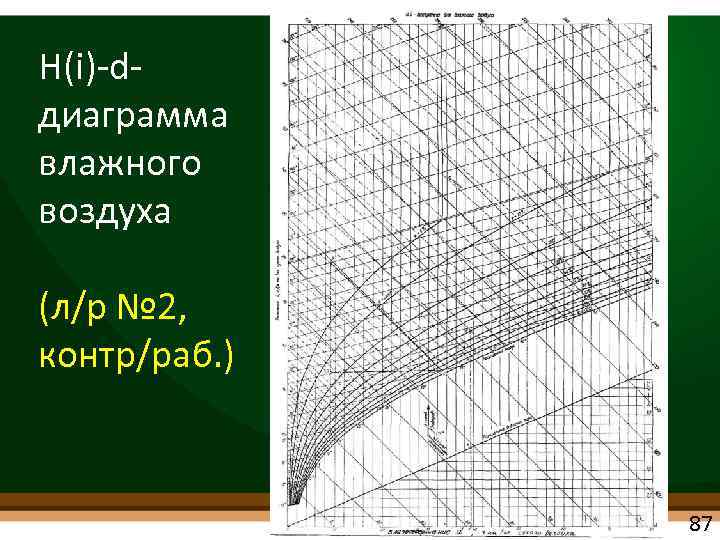H(i) d диаграмма влажного воздуха (л/р № 2, контр/раб. ) 87

ОСНОВЫ ТЕОРИИ ТЕПЛООБМЕНА (ТЕПЛОПЕРЕДАЧА) 88

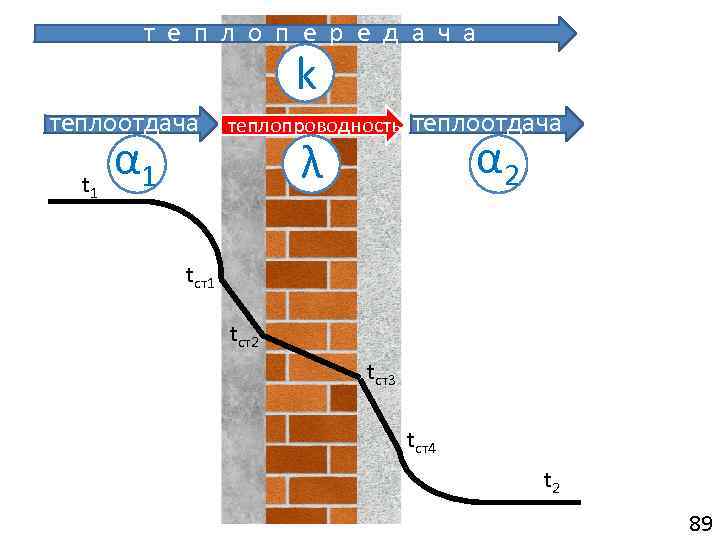т е п л о п е р е д а ч а k теплоотдача t 1 α 1 теплопроводность λ теплоотдача α 2 tcт1 tcт2 tcт3 tcт4 t 2 89

ТРИ ОСНОВНЫХ СПОСОБА (вида) переноса теплоты: ❶ теплопроводность ❷ конвекция чаще ❸ излучение 90

❶ ТЕПЛОПРОВОДНОСТЬ (Перенос теплоты в граничных условиях I рода) «жидкость» где q = Q/F , [Вт/м 2]- плотность теплового потока (удельный тепловой поток) - тепловой поток Q, отнесенный к единице площади F изотермической поверхности 91

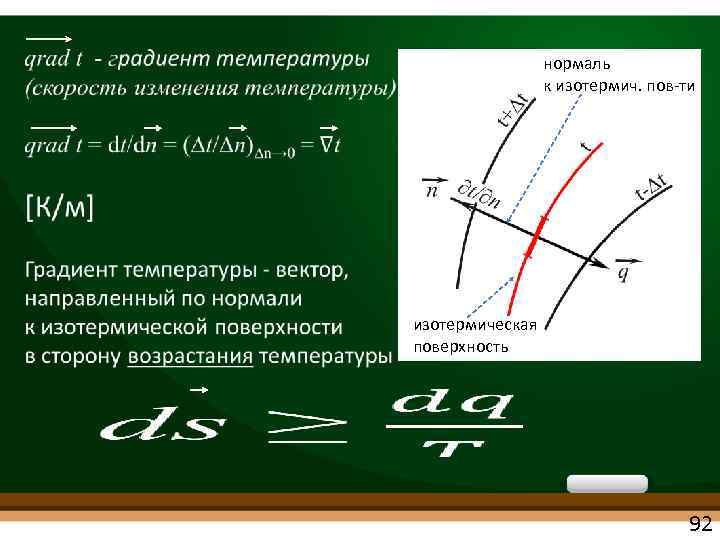нормаль к изотермич. пов ти изотермическая поверхность 92

λ коэффициент теплопроводности (теплопроводность) [Вт/(м. К)] количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности при температурном градиенте, равном 1 К/м. λ - величина справочная max 400 Вт/м. К – металлы (Cu, Ag) (графен, алмаз 1000 5300 Вт/м. К ) min 0. 02 0. 2 Вт/м. К (газы) 93

Порядок значения λ, Вт/(м. К) • • • Воздух 0. 025 Изоляция < 0. 1 Вода 0. 6 Сталь 45 Медь 400 94

❷ КОНВЕКЦИЯ • перенос теплоты при перемещении макроскопических частей жидкости (газ, кап. ж ть, расплав Ме) ТЕПЛООТДАЧА – перенос теплоты между движущейся жидкостью и тв. пов. (стенкой) (конв. + теплопр ть) Закон Ньютона-Рихмана • «с» параметр тв. поверхности (стенки) • «ж» параметр среды (жидкости, газа) 95

α коэффициент теплоотдачи , Вт/(м 2 К) количество теплоты, проходящее в единицу времени через единицу поверхности при разности температур между поверхностью и жидкостью, равной 1 градусу α – величина расчетная. Определяется: 1. из решения системы диф. уравнений (д. у. энергии + + д. у. движения + ур-е неразрывности (сплошности); 2. используя теории подобия (зная Re, Pr, Gr…. Nu) и размерностей; 3. экспериментально 96

Различают: • свободную (естественную) конвекцию (теплые массы имеют меньшую плотность и поднимаются вверх, холодные – вниз) • вынужденную конвекцию (под действием внешнего побудителя – насоса, вентилятора) α своб << α вынужд α ламинарное течение << α турбулентное α газ << α кап. жидкость << α конденс. пара 97

Порядок значения α 2 К) , Вт/(м • Свободная конвекция в газах 5 – 30 (л/р № 3) • Вынужденная конвекция в газах 100 500 • Вынужденная конвекция в воде 15000 (течение воды в трубах) (л/р № 4) • Конденсация пара: – пленочная 10 000 40000 (л/р № 4) – капельная до 100 000 98

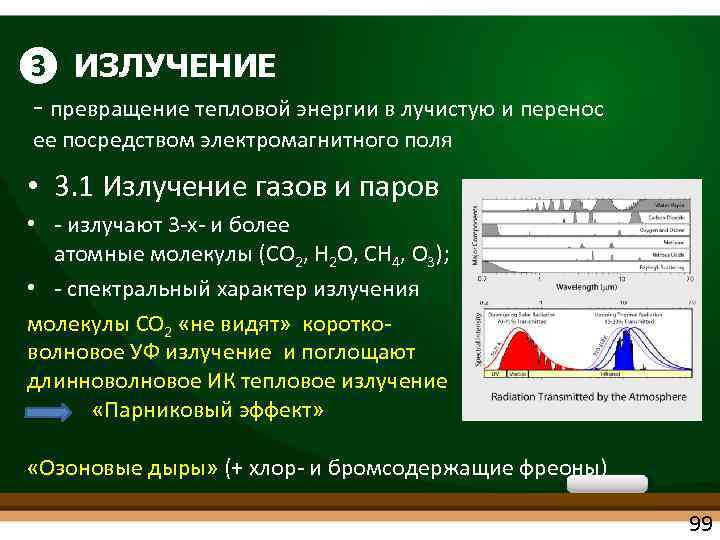❸ ИЗЛУЧЕНИЕ превращение тепловой энергии в лучистую и перенос ее посредством электромагнитного поля • 3. 1 Излучение газов и паров • излучают 3 х и более атомные молекулы (СО 2, Н 2 О, СН 4, О 3); • спектральный характер излучения молекулы СО 2 «не видят» коротко волновое УФ излучение и поглощают длинноволновое ИК тепловое излучение «Парниковый эффект» «Озоновые дыры» (+ хлор и бромсодержащие фреоны) 99

• 3. 2 Излучение твердых тел • сплошной (непрерывный) спектр излучения • поверхностный характер, не зависит от толщины тела (в отл. от объемного хар ра излучения газов) Закон Стефана Больцмана Йозеф Стефан Лю двиг Бо льцман Joseph Stefan 1835 -1893 Австро. Венгрия. Венский университет Ludwig Eduard Boltzmann 1844 -1906 Австро-В. Венский университет 100

Закон Стефана Больцмана q T 4 101

Основы гидравлики и теплотехники Лекция 5 102

ТЕПЛОПЕРЕДАЧА (Перенос теплоты в граничных условиях III рода) перенос теплоты от горячего теплоносителя к холодному через разделяющую стенку теплопроводность + конвекция + излучение λ α ε = теплопередача k чаще 103

Уравнение теплопередачи Q = k F t = k F (t 1 – t 2), q = k t = k(t 1 – t 2) • Индекс « 1» – горячий теплоноситель • Индекс « 2» – холодный теплоноситель t – температурный напор. (ср. арифметич. , ср. логарифмич. – см. ниже) k – коэффициент теплопередачи: Вт/(м 2 К) количество теплоты, проходящее в единицу времени через единицу поверхности при разности температур теплоносителей, равной 1 градусу 104

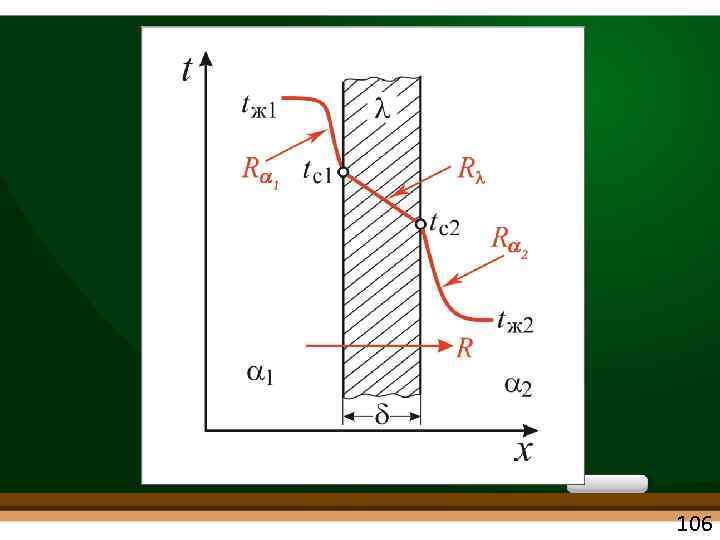
• где R – термическое сопротивление теплопередаче м 2 К/Вт Термическое сопротивление способность тела (поверхности или какого либо слоя) препятствовать распространению теплового движения микрочастиц (молекул, электронов, атомов). численно равно температурному напору, необходимому для передачи единичного теплового потока 1 Вт/м 2 к поверхности тела или через слой вещества 105

106

• термическое сопротивление частные термические теплопередаче сопротивления термическое сопротивление теплоотдаче от горячего теплоносителя к стенке термическое сопротивление теплоотдаче от стенки к холодному теплоносителю 107

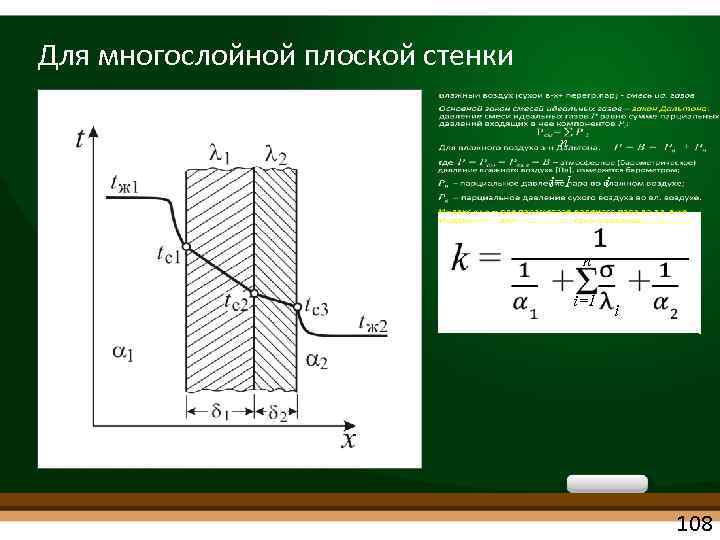Для многослойной плоской стенки n i=1 i 108

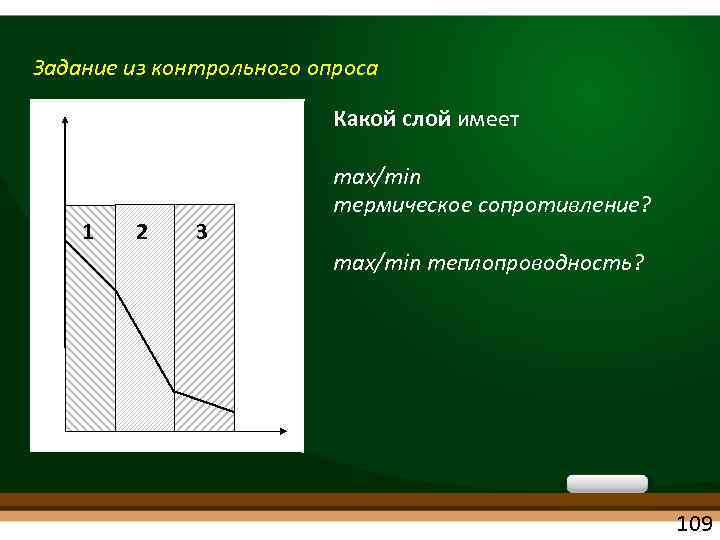Задание из контрольного опроса Какой слой имеет 1 2 3 max/min термическое сопротивление? max/min теплопроводность? 109

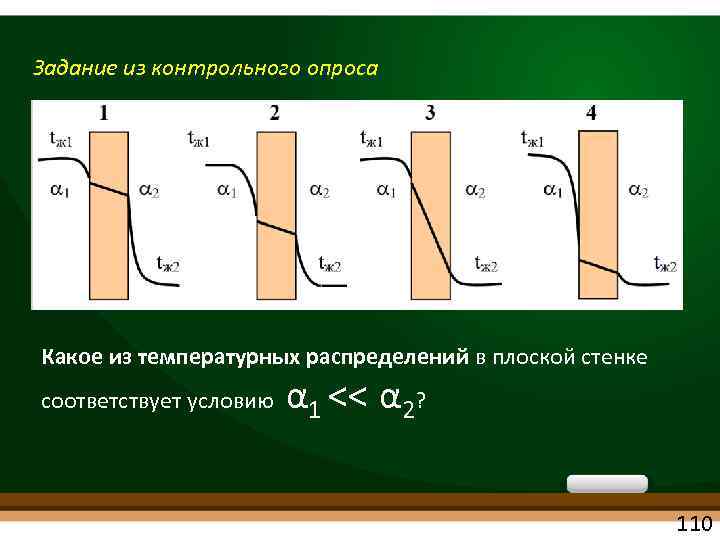Задание из контрольного опроса Какое из температурных распределений в плоской стенке α << α 2? соответствует условию 1 110

Для цилиндрической стенки линейное термическое сопротивление теплопередаче, [м. К/Вт] 111

Для цилиндрической стенки Линейное термическое сопротивление теплоотдаче от горячего теплоносителя к стенке от стенки к холодному теплоносителю Линейное термическое сопротивление теплопроводности слоя стенки 112

Интенсификация теплопередачи const q = k t Проведем анализ частных термических сопротивлений: Необх. : толщину стенки (прочность, стоимость) теплопроводность стенки (Cu, Ag) 113

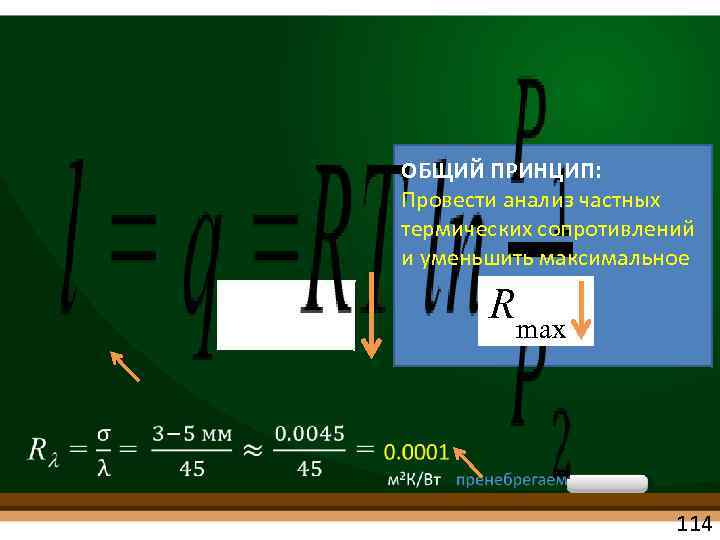ОБЩИЙ ПРИНЦИП: Провести анализ частных термических сопротивлений и уменьшить максимальное Rmax 114

R можно, например, оребрением Оребрение делают со стороны min α , где max R после ореберения F 1 F 2 до ореберения 115

Задание из контрольного опроса Если в теплообменнике горячий газ греет воздух, то оребрение: А делают со стороны холодного теплоносителя; Б делают со стороны горячего теплоносителя; В делают с обеих сторон; С не делают • 116

Задание из контрольного опроса 117

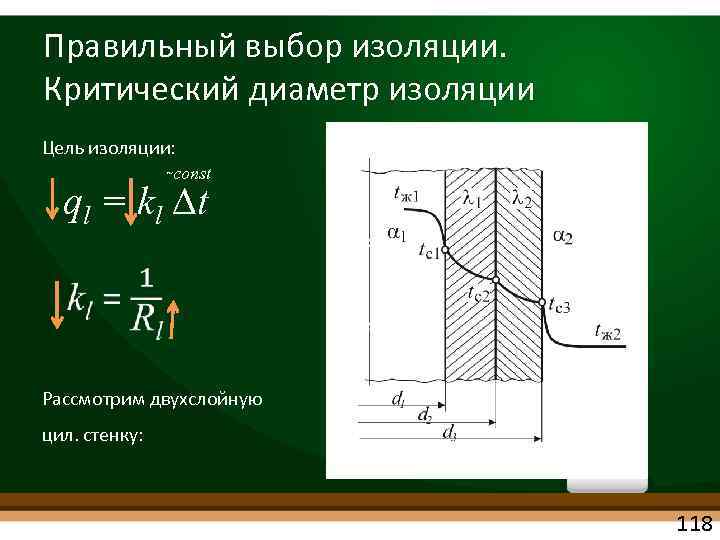Правильный выбор изоляции. Критический диаметр изоляции Цель изоляции: const ql = kl t Рассмотрим двухслойную цил. стенку: 118

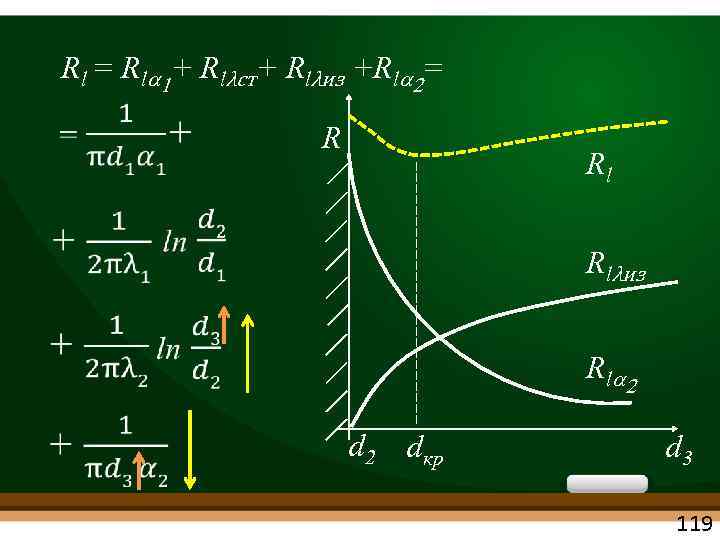Rl = Rla 1+ Rlλст+ Rlλиз +Rla 2= R Rl Rlλиз R la 2 d 2 dкр d 3 119

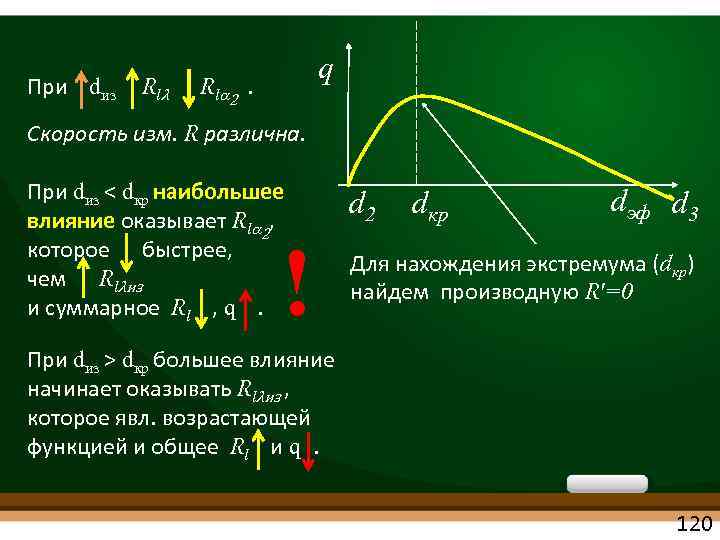При dиз Rlλ q Rla 2 . Скорость изм. R различна. При dиз < dкр наибольшее влияние оказывает Rla 2, которое быстрее, чем Rlλиз и суммарное Rl , q . ! d 2 dкр dэф d 3 Для нахождения экстремума (dкр) найдем производную Rʹ=0 При dиз > dкр большее влияние начинает оказывать Rlλиз , которое явл. возрастающей функцией и общее Rl и q. 120

Основы гидравлики и теплотехники Лекция 6 121

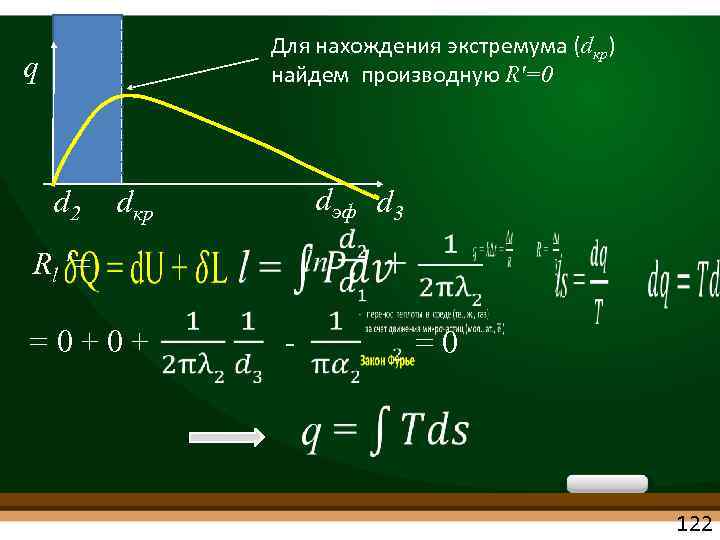Для нахождения экстремума (dкр) найдем производную Rʹ=0 q d 2 dкр Rl ʹ= =0+0+ dэф d 3 - =0 122

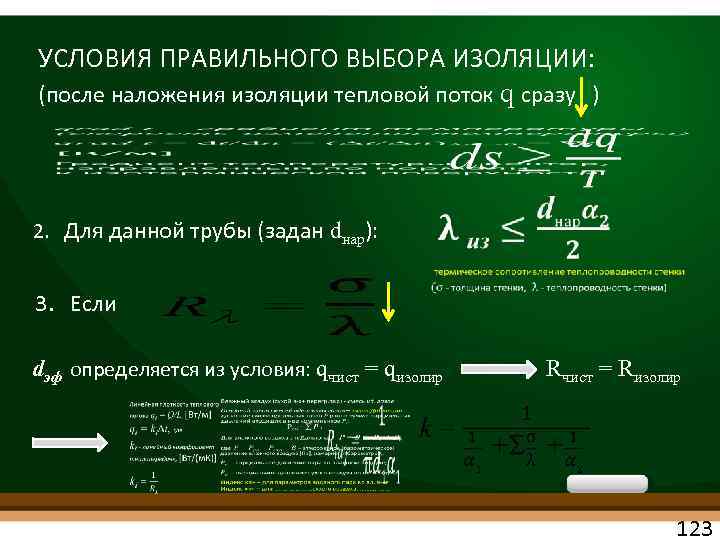УСЛОВИЯ ПРАВИЛЬНОГО ВЫБОРА ИЗОЛЯЦИИ: (после наложения изоляции тепловой поток q сразу ) 2. Для данной трубы (задан dнар): 3. Если dэф определяется из условия: qчист = qизолир Rчист = Rизолир 123

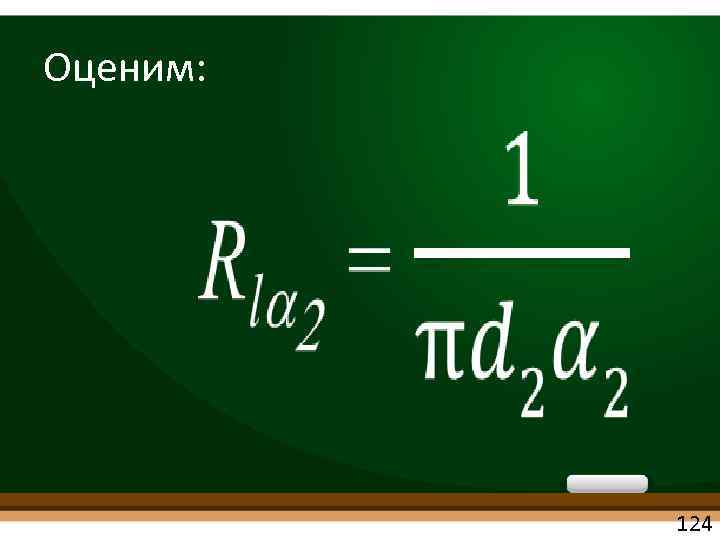Оценим: • 124

ЭЛЕМЕНТЫ ТЕОРИИ ПОДОБИЯ 3 вопроса, которые стоят перед экспериментатором: ? ? ? какие величины надо измерять в опыте как обрабатывать результаты опыта какие явления подобны 125

Различают: • подобные явления - качественно одинаковы и аналитически описываются одними уравнениями и по форме, и по содержанию. • аналогичные явления уравнения одинаковы по форме, но различны по физическому содержанию: Пример аналогичных явлений: теплопроводность и электропроводность: поток (теплоты q, электричества i) пропорционален градиенту (температуры – grad t, потенциала – grad U) – соотв. законы Фурье и Ома. • В подобных системах существуют особые величины, называемые инвариантами, или критериями подобия, или числами подобия. 126

Критерий (число) подобия - безразмерный комплекс, составленный из размерных величин, характеризующих данное явление. Критерии подобия принято называть именами ученых, работающих в этой области, и обозначать двумя начальными буквами их фамилии, например, Nu – критерий (число) Нуссельта (Nusselt) Re – критерий (число) Рейнольдса (Reynolds) Осборн Рейнольдс (O. Reynolds) 1842 -1912 — английский инженер и физик, основоположник гидродинамики Вильгельм Нуссельт (W. Nusselt) 1882 -1957 — немецкий физик, В 1915 году впервые предложил исп. безразмерные группы в теории теплообмена 127

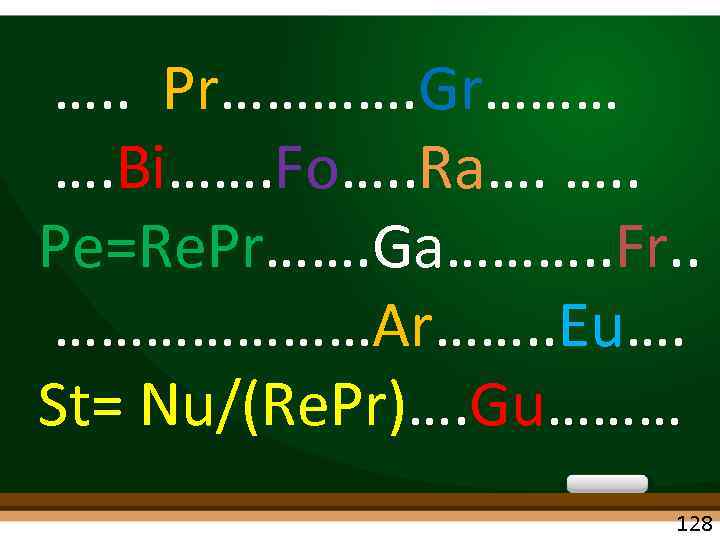…. . Pr…………. Gr……… …. Bi……. Fo…. . Ra…. …. . Pe=Re. Pr……. Ga………. . Fr. . …………………Ar……. . Eu…. St= Nu/(Re. Pr)…. Gu……… 128

Критерий подобия можно получить для любого физического явления: 1. приведением к безразмерному виду диф. ур-ий, описыв. рассматриваемое явление. 2. на основе анализа размерностей, когда рассматривается новый процесс, для которого аналитич. описания еще нет ТЕОРЕМЫ ПОДОБИЯ I теорема подобия: подобные между собою явления имеют одинаковые критерии подобия. II теорема подобия: зависимость между переменными, характеризующими явление, может быть представлена в виде зависимости между критериями подобия (критериальным уравнением). 129

III теорема подобия: (обратная теорема подобия, теорема Кирпичева—Гухмана): необхо димыми и достаточными условиями для создания подобия являются про порциональность сходственных параметров, входящих в условия одно значности, и равенство критериев подобия сопоставляемых явлений. Условия однозначности: геометрические, физические, начальные, граничные (краевые) Критерии, входящие в условия однозначности определяющие. …………. не входящие в условия однозначности определяемые. Явления подобны, если определяющие критерии инвариантны (одинаковы).

ОТВЕТЫ НА ПОСТАВЛЕННЫЕ ВОПРОСЫ: Какие величины надо измерять в опыте ? (I теорема подобия) в опытах надо измерять величины, которые содержатся в критериях подобия изучаемого явления Как обрабатывать результаты опыта? (II теорема подобия) результаты опытов надо представлять в виде критериальных зависимостей Какие явления подобны? (III теорема подобия) подобны те явления, у которых подобны условия однозначности и равны определяющие критерии 131

Основные критерии подобия тепловых процессов Критерий (число) Нуссельта Определяемый критерий Физ. смысл: Мера интенсивности теплоотдачи на границе раздела фаз. Безразмерный коэффициент теплоотдачи где α коэффициент теплоотдачи λ коэффициент теплопроводности теплоносителя l определяющий (характерный) размер (выбирается для конкретного случая. Часто l=d) 132

l определяющий (характерный) размер При расчете теплоотдачи вдоль: l=dнар вертикальных труб l=h (высота трубы), [поперек l=dнар] горизонтальных труб Вдоль пластин ахb: l=а (размер вдоль движения потока) a b Внутри труб круглого сечения d l=d ! 133

определяющая температура – температура, при которой берутся теплофизические свойства из таблиц «ж» – при средней температуре жидкости «ст» – при средней температуре стенки «г» – при средней температуре 0. 5 (tж+ tст) 134

Определяющие критерии Число Прандтля Мера соотношения вязкостных и температуропроводных св в теплоносителей; мера соотношения полей скоростей и т р в потоке Величина справочная (см. табл. св-в вещества) ν – кинематич. вязкость, [м 2/с], а – температуропроводность, [м 2/с] – см. табл. св в Число Рейнольдса Мера соотношения сил инерции и сил вязкого трения Re < 2300 – ламинарный режим теч. Re > 10 000 – турбулентный режим w – скорость течение теплоносителя, [м/с] – опр. из уравнения массового расчета 135

Определяющие критерии Число Грасгофа Franz Grashof Мера соотношения сил трения, инерции и подъемной (архимедовой) силы, определяемой разностью плотностей в разл. точках неизотермич. потока при свободной конвекции где d – диаметр трубки, м; ν – кинематическая вязкость, м 2/с; а – температуропроводность, м 2/с; lж – теплопроводность жидкости, Вт/(м. К); t = tс – tж – температурный напор, К; g = 9. 8 – ускорение свободного падения, м/с2; b – температурный коэффициент объемного расширения, для газов , b = 1/ Тж , 1/ К; Тж – температура газа, К. 1826 1893 136

Используя критерии (числа) подобия, можно определить коэффициент теплоотдачи (см. лаб. /раб. ): Для определения числа Нуссельта Nuж используют различные критериальные зависимости (чаще степенные): Для свободной конвекции Nu = f ( Gr, Pr ) Nu = A (Gr. Pr)n Для вынужденной конвекции Nu = f ( Re, Pr ) Nu = C Ren Prm 137

Для свободной конвекции 3 около горизонтальных труб Л/Р № Nuж= 0. 5(Grж. Prж)0. 25 Число Грасгофа Число Прандтля Prж (см. табл. св в) 138

При движении жидкости в трубах (турбулентный режим) ф ла Михеева Число Рейнольдса α 2 Л/Р № 4 Число Прандтля (см. табл. св в жидкости) Prж - при ср. т-ре жидкости Prст - при ср. т-ре стенки Величины, входящие в формулы – см. конспект Л/Р 139

При пленочной конденсации пара на горизонтальных трубах: α 1 Л/Р № 4 Nuж = 0. 728 (Gaж Kж Prж)0. 25 Число Галилея Число фазового превращения Все теплофизические свойства (кроме r) – свойства конденсата (воды) при температуре конденсата (пара) (см. табл. св-в воды) 140

Основы гидравлики и теплотехники Лекция 7 141

ОСНОВЫ РАСЧЕТА ТЕПЛООБМЕННИКОВ Виды теплообменников: РЕКУПЕРАТИВНЫЕ оставить строчку две РЕГЕНЕРАТИВНЫЕ СМЕСИТЕЛЬНЫЕ 142

РЕКУПЕРАТИВНЫЕ ТО 143

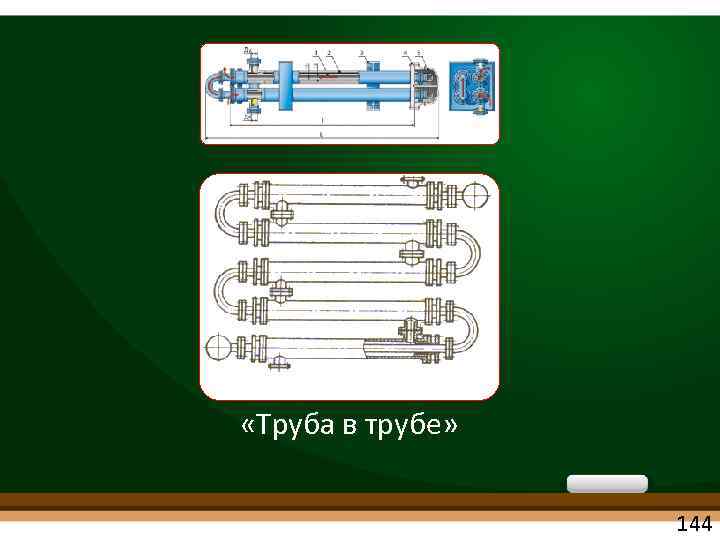«Труба в трубе» 144

145

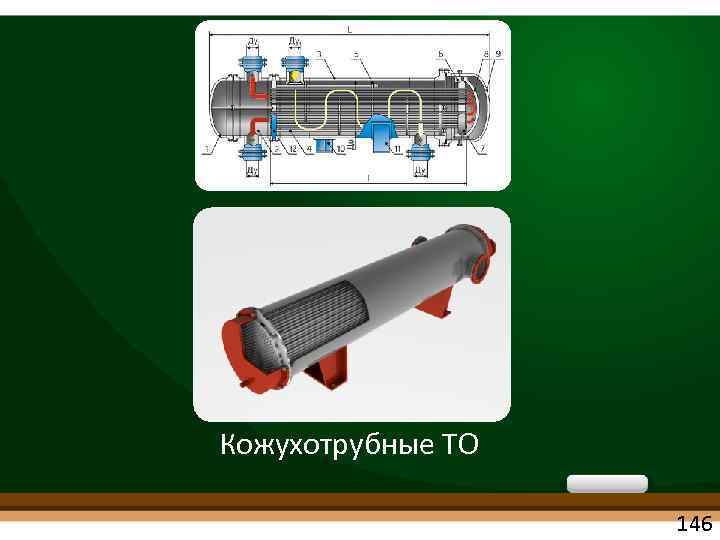Кожухотрубные ТО 146

147

Пластинчатые ТО 148

149

150

151

152

153

154

155

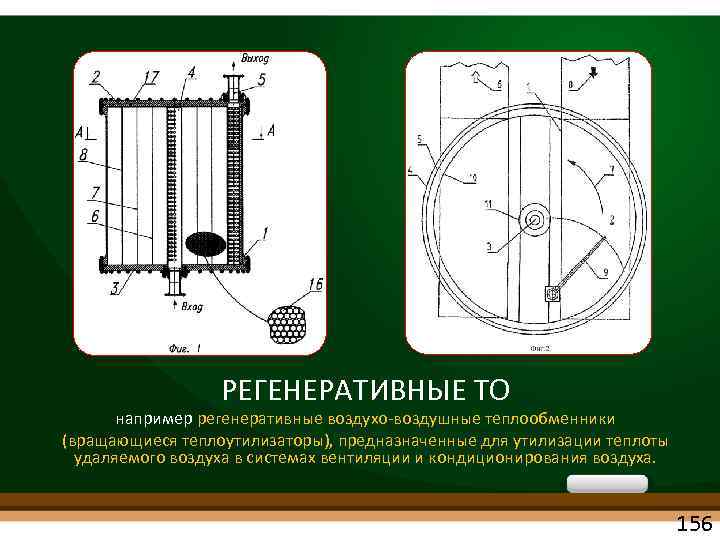РЕГЕНЕРАТИВНЫЕ ТО например регенеративные воздухо воздушные теплообменники (вращающиеся теплоутилизаторы), предназначенные для утилизации теплоты удаляемого воздуха в системах вентиляции и кондиционирования воздуха. 156

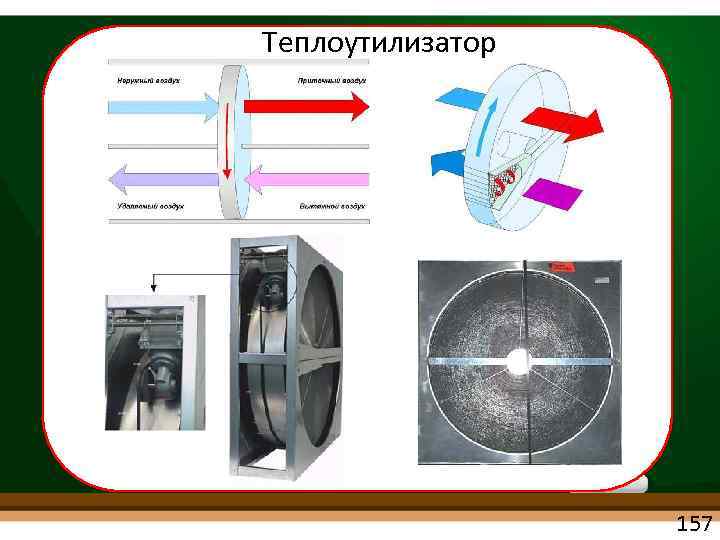Теплоутилизатор 157

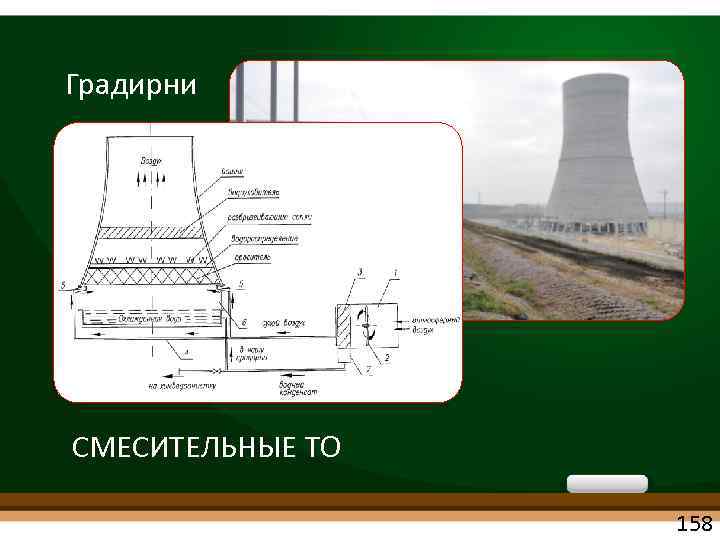Градирни СМЕСИТЕЛЬНЫЕ ТО 158

Градирни СМЕСИТЕЛЬНЫЕ ТО 159

ССО МГСУ 2012 Строительство Нововоронежской АЭС 160

ОСНОВЫ РАСЧЕТА ТЕПЛООБМЕННИКОВ Виды теплообменников: РЕКУПЕРАТИВНЫЕ – непрерывного действия, теплоносители разделены стенкой РЕГЕНЕРАТИВНЫЕ – для запыленных, агрессивных, высокоt. сред (t > 1000 °С); доп. промежут. теплоноситель (наполнитель). Периодич. (часто) СМЕСИТЕЛЬНЫЕ – прямое смешивание сред градирни (охл. воды потоком воздуха) 161

Виды расчета ТО 1. Конструктивный • Дано: параметры т/нос. на входе и выходе из ТО • Найти: поверхность ТО 2. Поверочный • Дано: параметры т/нос. на входе и поверхность ТО • Найти: параметры т/нос. на выходе из ТО (проверить пригодность данного теплообменника). 162

Основные уравнения 1 • УТП конструктивного расчета 2 • УТБ рекуперативного теплообменного аппарата 3 • УМР 163

1 Уравнение теплового баланса • для определения теплового потока потери ~0 Q 1 = Q 2 = Q + Q отдано гор. т/нос. = принято хол. т/нос. Q По I з ну ТД для изобарного процесса qр = i = (i" – i' ) Q = Мq = М i Уравнение теплового баланса в общем виде: 164

• Для веществ, не меняющих агрегатное состояние: i = ср t = ср(t" – t' ) (c/р «Труба в трубе» ) 165

• Для веществ, не меняющих агрегатное состояние: i = ср t = ср(t" – t' ) (c/р «Труба в трубе» ) Для пароводяного ТО (л/р № 4): Q 2 = М 2 q = М 2 ср2 t 2 = М 2 ср2(t"2 – t'2) Q 1 = М 1 q = М 1 i 1 = М 1 (i'1 – i"1) 166

2 Уравнение теплопередачи • для определения поверхности теплообмена Q = k. FDt Тепловой поток (из УТБ) F Температурный напор (см. ниже) Коэффициент теплопередачи 167

• ЧВС (для течения воды в трубах) 3 Уравнение массового расхода w = М / ρ f – cкорость течения т/носителя, м/c М = ρwf ρ – плотность данного теплоносителя, кг/м 3 f – площадь поперечного сечения, м 2 168

Вернемся к t в уравнении теплопередачи: t – средний температурный напор, °С, • можно определить как средний логарифмический напор • при определяется как средний арифметический напор • где и – средние температуры теплоносителей; • tб и tм – наибольшая и наименьшая разность температур между теплоносителями на входе и выходе теплообменника Для >>-ва инж. расчетов можно исп. ср. арифметич. (<4%) 169

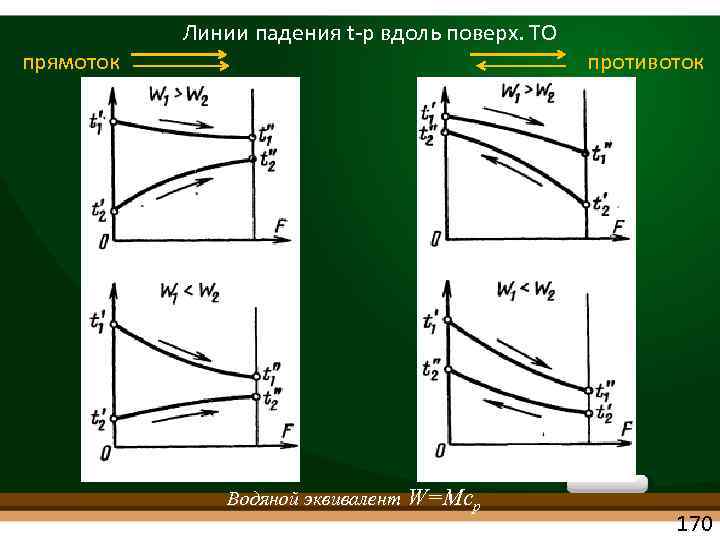прямоток Линии падения t р вдоль поверх. ТО противоток с Водяной эквивалент W=Mcp 170

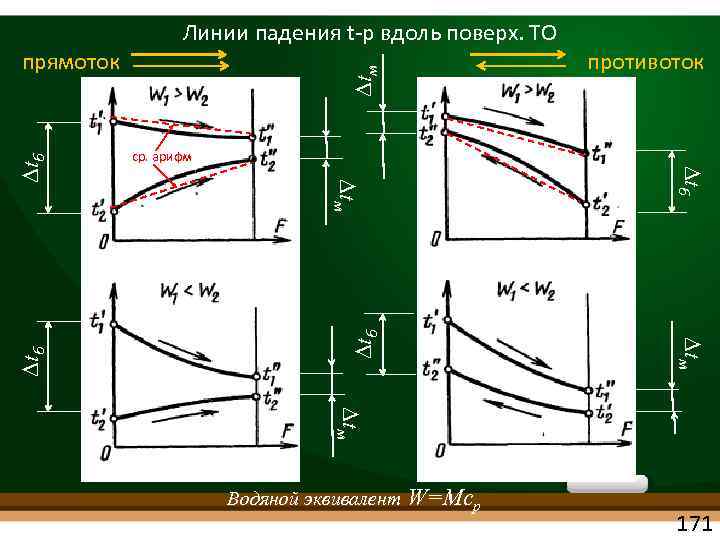tм tб tб с tб противоток ср. арифм tб прямоток Линии падения t р вдоль поверх. ТО tм Водяной эквивалент W=Mcp 171

Сравнение прямотока и противотока Можно показать, что при тех же температурах теплоносителей Ср. лог. t рн. напор при противотоке всегда ср. лог. t рн. напора при прямотоке Q=Q Q = k F t 1. F=F Q = k F t 2. F При одинак. мощности ТО: Противоточный ТО более компактный При одинак. габаритах: В противотоке можно нагреть до более высокой t 172

конечной т ры" src="https://present5.com/presentation/-42717226_223646722/image-173.jpg" alt="В противотоке конечная т ра холодного т/нос. t"2 может быть > конечной т ры" /> В противотоке конечная т ра холодного т/нос. t"2 может быть > конечной т ры горячего т/нос. с t"1 В прямотоке всегда t"2 < t"1 173

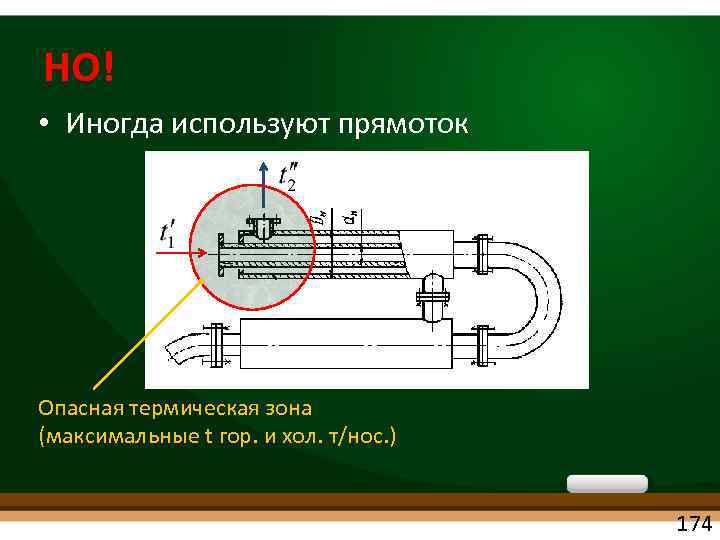НО! • Иногда используют прямоток Опасная термическая зона (максимальные t гор. и хол. т/нос. ) 174

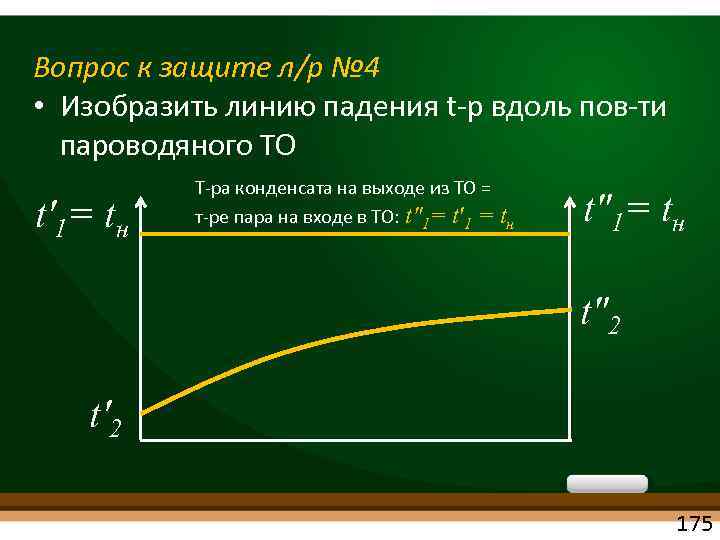Вопрос к защите л/р № 4 • Изобразить линию падения t р вдоль пов ти пароводяного ТО t'1= tн Т ра конденсата на выходе из ТО = т ре пара на входе в ТО: t"1= t'1 = tн t"1= tн t"2 t'2 175

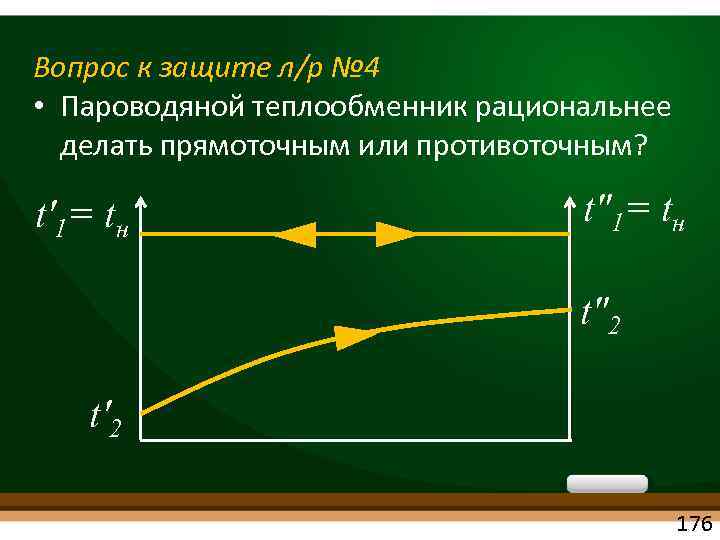Вопрос к защите л/р № 4 • Пароводяной теплообменник рациональнее делать прямоточным или противоточным? t'1= tн t"2 t'2 176

Вопрос к защите л/р № 4 • Пароводяной теплообменник рациональнее делать прямоточным или противоточным? Ответ • Если один из теплоносителей кипит или конденсируется (t = const), то ПРЯМОТОК = ПРОТИВОТОКУ 177