Теплопередача Примеры решения задач ТЕПЛОНОСИТЕЛИ — вещества

Теплопередача Примеры решения задач

ТЕПЛОНОСИТЕЛИ - вещества, участвующие в процессе переноса тепла 2 основных способа проведения тепловых процессов: • Передачей тепла через стенку • Путем непосредственного соприкосновения теплоносителей РАЗЛИЧАЮТ: СТАЦИОНАРНЫЙ ПРОЦЕСС – в каждой точке аппарата температура не изменяется во времени; осуществляется в аппаратах непрерывного действия НЕСТАЦИОНАРНЫЙ ПРОЦЕСС – осуществляется в аппаратах периодического действия, при пуске и остановке аппаратов непрерывного действия Передача тепла от одного тела к другому может происходить посредством: теплопроводности, конвекции, лучеиспускания

Уравнение теплового баланса Qгор=Qхол + Qпотерь, Если потери тепла малы, Qгор=Qхол

Частные случаи 1. Теплообмен без изменения агрегатного состояния теплоносителей Qгор= Gгорcгор(tн. гор- tк. гор) Qхол= Gхолcхол(tк. хол- tн. хол) Gгорcгор(tн. гор- tк. гор)= Gхолcхол(tк. хол- tн. хол) G 1 c 1(t 1 н- t 1 к)= G 2 c 2(t 2 к- t 2 н)

Частные случаи 2. Нагревание жидкости при конденсации водяного пара G 2 c 2(t 2 к- t 2 н)= G 1 r 1; r 1=i 1 -c 1 t 1

Задача 1 ¡ Определить общую тепловую нагрузку и необходимое количество охлаждающей воды для охлаждения в теплообменнике 2385 л/час нормального бутилового спирта от 90 о. С до 50 о. С, если начальная температура воды 18 о. С, а конечная – 32 о. Потерями тепла в окружающее пространство пренебречь. Общую тепловую нагрузку выразить в ккал/час , Дж/час, Дж/с

Решение Q=G 1 c 1(t 1 н- t 1 к)= G 2 c 2(t 2 к- t 2 н) G 2=v 1ρ1 c 1 (t 1 н- t 1 к)/ c 2(t 2 к- t 2 н)= =2. 385*810*0. 7(90 -50)/1*(32 -18)= =54000/14=3860 кг/час=3, 86 м 3/час Q=54000 ккал/час=54000*4, 19 к. Дж/час= =226000 к. Дж/час=226000/3600 к. Дж/час= = 62600 Вт (Дж/сек) Значения плотности и теплоемкости жидкостей – из таблиц

Задача 2 ¡ Какова была бы конечная температура охлаждающей воды в предыдущей задаче, если бы расход уменьшили вдвое при прочих постоянных условиях?

Решение Q=G 1 c 1(t 1 н- t 1 к)= G 2 c 2(t 2 к- t 2 н)=54000 ккал/час 54000=1*(t 2 k-18)3860/2 t 2 k=18+2*54000/3860=18+28=46 o. C

Задача 3 ¡ Жидкий бензол в количестве 1, 5 т/час подогревается в теплообменнике от 15 о до 55 о насыщенным водяным паром с давлением 1 ати. Каков расход греющего пара, если конденсат удаляется при температуре конденсации пара? Потерями пренебречь.

Решение Q= G 2 c 2(t 2 к- t 2 н)=G 1 r 1=G 1(i 1 -c 1 t 1) i 1=647 ккал/кг – энтальпия пара при 2 ата c 2=0, 41 – теплоемкость бензола при t=(55+15)/2 Q=1500*0. 41(55 -15)=24600 ккал/час G 1=24600/(647 -1*120)=46. 5 кг/час

Основное уравнение теплопередачи Q=k. F . Δ t ср Δtср- разность температур между горячим и холодным теплоносителем – движущая сила процесса – температурный напор F – поверхность теплопередачи Q – количество тепла, передаваемого в единицу времени k – коэффициент теплопередачи

k – коэффициент теплопередачи Физический смысл: - количество тепла, которое передается за единицу времени через поверхность 1 м 2 при средней разности температур в 1 о ¡

Средняя разность температур Δtср прямоток t 1 н t 2 н ¡ противоток t 1 к t 2 к t 1 н t 1 к t 2 к Δtср=(Δtб- Δtм)/[2. 3 lg (Δtб/Δtм)] Δtб/Δtм≥ 2 – для прямотока ¡ Δtср=(Δtб+Δtм)/2, Δtб/Δtм<2 - для противотока t 2 н

Задача 4 ¡ ¡ Определить среднюю разность температур и поверхность теплопередачи в предыдущей задаче с нагревом жидкого бензола водяным паром, если коэффициент теплопередачи равен 590 ккал/м 2 час. град. Сопоставить точность при расчете разности температур среднеарифметической и среднелогарифмической.

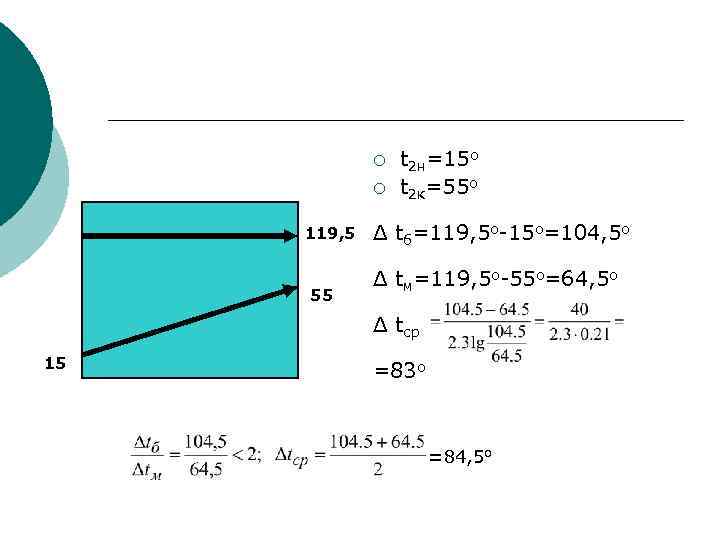¡ ¡ 119, 5 55 t 2 н=15 о t 2 к=55 о Δ tб=119, 5 о-15 о=104, 5 о Δ tм=119, 5 о-55 о=64, 5 о Δ tср 15 =83 о =84, 5 о

¡ В этом случае один из теплоносителей имел постоянную температуру, поэтому разность температур не зависит от направления движения теплоносителей. В общем случае это не так. При одинаковых начальных и конечных температурах теплоносителей при противотоке Δtср выше и требуемая поверхность теплообмена меньше, чем при прямотоке