Теплопередача-14(СВОБОДНОМ ДВИЖЕНИИ ЖИДКОСТИ).ppt
- Количество слайдов: 38

ТЕПЛООТДАЧА ПРИ СВОБОДНОМ ДВИЖЕНИИ ЖИДКОСТИ ОСНОВНЫЕ ПОЛОЖЕНИЯ Свободное движение возникает за счет неоднородного распределения в рассматриваемой жидкости массовых (объемных) сил. Такими силами являются сила тяжести, центробежная сила и силы за счет наведения в жидкости электромагнитного поля высокой напряженности. Наиболее хорошо изучено свободное движение жидкости, вызванное гравитационным в силами. (A) В уравнении движения гравитационные силы учитываются членом , имеющим размерность силы, отнесенной к единице объема. При теплообмене температура жидкости переменна, поэтому возникает разность плотностей и как следствие разность гравитационных сил, представляющих собой архимедову или подъемную (опускную) силу.

В технических задачах ускорение силы тяжести от точки к точке рассматриваемого пространства практически не изменяется. Объемные же силы, вызванные центробежным эффектом или электромагнитным полем, могут изменяться в изучаемой жидкости за счет изменения вектора , представляющего собой отношение силы, действующей на данный элемент жидкости, к массе этого элемента. Если учитывается только сила тяжести, то. Будет рассмотрена теплоотдача только при свободном гравитационном движении. Иногда результаты, полученные для гравитационной конвекции, применяют для оценки свободного движения под действием других массовых сил. Тогда ускорение силы тяжести заменяют суммой ускорения g и ускорения, соответствующего дополнительно действующей массовой силе (например, центробежного ускорения 2/r). Полученный таким образом результат следует рассматривать как приближенный, так как поле ускорений, соответствующих различным силам, может отличаться от поля гравитационного ускорения.

10 -2. ТЕПЛООТДАЧА ПРИ СВОБОДНОМ ДВИЖЕНИИ ЖИДКОСТИ В БОЛЬШОМ ОБЪЕМЕ Будет рассмотрено свободное гравитационное течение для наиболее простых форм поверхности твердого тела (вертикальная плита, горизонтальный цилиндр). Предполагается, что объем жидкости настолько велик, что свободное движение, возникающее у других тел, расположенных в этом объеме, не сказывается на рассматриваемом течении. Как и при вынужденной конвекции, свободное движение жидкости может быть как ламинарным, так и турбулентным. А. Теплоотдача при свободном ламинарном движении вдоль вертикальной пластины Пусть вертикальная пластина с неизменной температурой поверхности, равной tс находится в жидкости или газе Жидкость вдали от пластины неподвижна (вынужденное течение отсутствует), температура жидкости вдали от пластины постоянна и равна t 0. Примем, что tc > to (однако полученные результаты будут справедливы и для обратного соотношения температур). При этом у пластины появляется подъемное движение нагретого слоя жидкости.
Вдали от пластины скорость по-прежнему равна нулю. Расположим начало координат у нижней кромки пластины, а ось Оу нормально к ее поверхности (рис. 10 -1). Будем полагать, что пластина вдоль оси Oz бесконечна. Процесс стационарный. Рис 10 -1. К выводу формулы для коэффициента теплоотдачи при свободной тепловой конвекции

Для упрощения решения задачи примем следующие допущения: 1) силы инерции пренебрежимо малы по сравнению с силами тяжести и вязкости; 2) конвективный перенос теплоты, а также теплопроводность вдоль движущегося слоя жидкости можно не учитывать; 3) градиент давления равен нулю; 4) физические параметры жидкости (исключая плотность) постоянны; плотность является линейной функцией температуры.

Будем полагать, что температура в движущемся слое жидкости изменяется по уравнению (10. 1) где = t — t 0 и c = tc — t 0 согласно условию задачи c = const. Уравнение (10 -1) удовлетворяет граничным условиям: (а) Коэффициент теплоотдачи определяется уравнением (10. 2) Из уравнения (10 -1) следует, что

Подставляя значение получаем: в уравнение теплоотдачи (10 -2), (10. 3) Толщина движущегося слоя жидкости переменна по высоте и связана со скоростью движения в этом слое. Поле скоростей описывается уравнением движения. При принятых условиях течение происходит в основном в направлении оси Ох, поэтому используем уравнение движения только в проекциях на ось Ох. Для стационарного течения и с учетом ранее принятых допущений уравнение движения упрощается. В результате вместо уравнения (а) будем иметь: (10. 4) При линейной зависимости плотности от температуры где = const. Отсюда

Подставляя значение согласно (10 -1) в уравнение (10 -4) и учитывая последнее соотношение для плотности, уравнение движения можно написать следующим образом: или здесь Интегрирование уравнения движения дает: и (б)

Примем следующие граничные условия для скорости: x = 0 как при y = 0, так и при у = . Отметим, что строго говоря, при у= ( = 0) скорость может быть не равна нулю. Это объясняется действием сил вязкости. Движущиеся частицы могут увлекать за собой слон жидкости, находящиеся в изотермических условиях. При принятых граничных условиях из уравнения (б) следует, что и C 2 = 0 Подставив значения С 1 и С 2 в уравнение (б) и произведя некоторые преобразования, получим следующее уравнение распределения скоростей в движущемся слое жидкости: (10. 5)
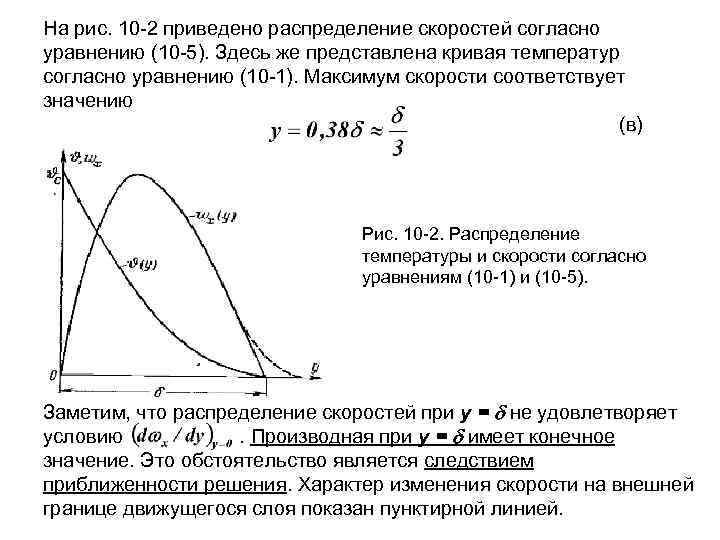
На рис. 10 -2 приведено распределение скоростей согласно уравнению (10 -5). Здесь же представлена кривая температур согласно уравнению (10 -1). Максимум скорости соответствует значению (в) Рис. 10 -2. Распределение температуры и скорости согласно уравнениям (10 -1) и (10 -5). Заметим, что распределение скоростей при у = не удовлетворяет условию. Производная при у = имеет конечное значение. Это обстоятельство является следствием приближенности решения. Характер изменения скорости на внешней границе движущегося слоя показан пунктирной линией.

Согласно уравнению (10 -5) среднеинтегральная скорость равна: (10. 6) Для простоты решения среднюю температуру жидкости в слое определим приближенно как среднеинтегральную по сечению слоя: (10. 7) Таким образом, принятых условиях величина средней температуры слоя не зависит от координаты x.

Расход жидкости через поперечное сечение слоя 1 равен: (10. 8) (г) Расход жидкости определен по плотности о. При этом полагаем, что жидкость плотностью о, вовлекаясь в движущийся слой, приобретает в среднем скорость х. Подставляя в (г) значение х согласно уравнению (10 -6), получаем: (д)

В движение вовлекается жидкость с первоначальной температурой t 0. В движущемся слое эта жидкость нагревается до различных температур, лежащих в интервале от t 0 до tc. Можно считать, что в среднем жидкость нагревается до температуры. На этот нагрев затрачивается теплота (е) Из уравнения (е) следует, что (ж)

Приравнивая правые части уравнений (д) и (ж), получаем дифференциальное уравнение, описывающее изменение по высоте стенки: (з) Интегрируя это уравнение, получаем: (и) Постоянную интегрирования с найдем из условия, что при х = 0. Отсюда с = 0

Из уравнения (и) следует, что (10. 9) Согласно уравнению (10 -3). Подставляя сюда значение , получаем: (10. 10) Приведем уравнение (10 -10) к безразмерному виду, правую части уравнения умножим на х и разделим на .

После некоторых преобразований получим: (10. 11) и Как следует из уравнения (10 -11), Nux=f(Gr Pr). Такой же результат дает теория подобия. Произведение чисел Gr и Рr часто называют числом Рэлея и обозначают символом Ra.

В рассматриваемом случае температуры tc и t 0 постоянны, следовательно, неизменен и температурный напор c = tc — t 0. Из уравнения (10. 11) следует, что = сx-0, 25, где с f(х). При этом где х=l — местный коэффициент теплоотдачи в точке, определяемой координатой х=l. Тогда средняя теплоотдача вертикальной пластины при tс = const в ламинарном течении (10. 12) Коэффициенты пропорциональности в формулах (10 11) и (10 -12) нуждаются в некоторых уточнениях. Формулы (10 -11) и (10 -12) получены при ряде упрощающих допущений. В частности, при выводе этих формул не учитывались силы инерции. Расчеты, проведенные с учетом сил инерции, показывают, что коэффициент пропорциональности в формулах (10 -11) или (10 -12) зависит от числа Прандтля.
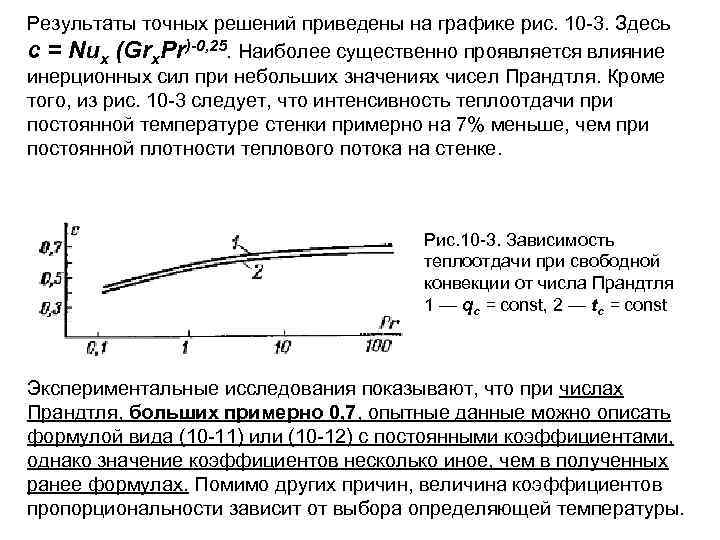
Результаты точных решений приведены на графике рис. 10 -3. Здесь с = Nux (Grx. Pr)-0, 25. Наиболее существенно проявляется влияние инерционных сил при небольших значениях чисел Прандтля. Кроме того, из рис. 10 -3 следует, что интенсивность теплоотдачи при постоянной температуре стенки примерно на 7% меньше, чем при постоянной плотности теплового потока на стенке. Рис. 10 -3. Зависимость теплоотдачи при свободной конвекции от числа Прандтля 1 — qc = const, 2 — tc = const Экспериментальные исследования показывают, что при числах Прандтля, больших примерно 0, 7, опытные данные можно описать формулой вида (10 -11) или (10 -12) с постоянными коэффициентами, однако значение коэффициентов несколько иное, чем в полученных ранее формулах. Помимо других причин, величина коэффициентов пропорциональности зависит от выбора определяющей температуры.
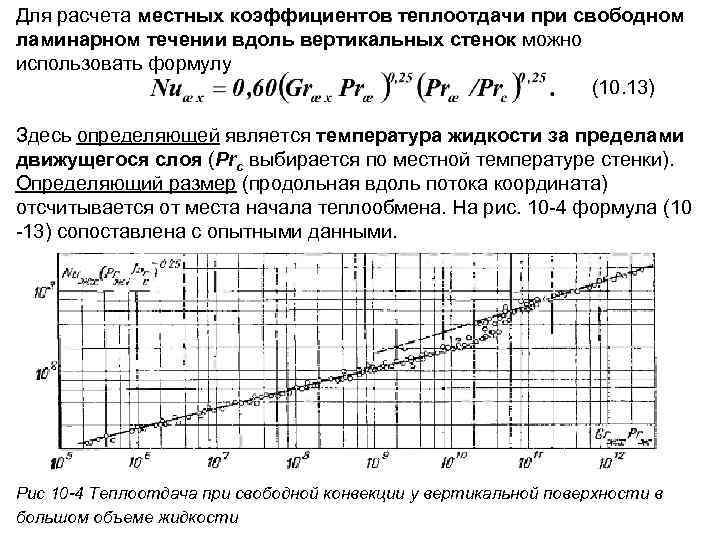
Для расчета местных коэффициентов теплоотдачи при свободном ламинарном течении вдоль вертикальных стенок можно использовать формулу (10. 13) Здесь определяющей является температура жидкости за пределами движущегося слоя (Prc выбирается по местной температуре стенки). Определяющий размер (продольная вдоль потока координата) отсчитывается от места начала теплообмена. На рис. 10 -4 формула (10 -13) сопоставлена с опытными данными. Рис 10 -4 Теплоотдача при свободной конвекции у вертикальной поверхности в большом объеме жидкости

Формула (10 -13) получена при условии, что qc = const. Осредняя коэффициенты теплоотдачи, получаем, что при qc = const Тогда расчетная формула для средних коэффициентов теплоотдачи будет: (10. 14) Здесь определяющей температурой является температура жидкости за пределами движущегося слоя, определяющий размер — длина пластины, отсчитываемая от начала теплообмена. Формула (10 -13) получена для теплоносителей с числами Прандтля от 0, 7 до 3 103. Ею следует пользоваться при 103 < Grжх. Рrж <109. Уравнение (10 -13) получено при условии qc = const. Исходя из графика рис. 10 -3, для случая tc = const значение коэффициента пропорциональности в формуле (10 -13) в первом приближении может быть взято равным примерно 0, 55. При этом

Теплоотдача при свободном турбулентном движении вдоль вертикальной пластины Развитое турбулентное течение наступает при числах Grжх. Рrж 6 1010 (рис. 10 -4). Для местных коэффициентов теплоотдачи при развитом турбулентном течении предложена формула (10. 15) Определяющие температура и линейный размер выбраны так же, как и в формуле (10 -13). Линейный размер входит в числа Nu и Gr: и Отсюда следует, что при развитом турбулентном течении коэффициент теплоотдачи не зависит от линейного размера и, следовательно, местный коэффициент теплоотдачи равен среднему.

Теплоотдача при переходном режиме свободного движения вдоль вертикальной пластины Согласно опытным данным различных исследователей переходный режим имеет место примерно при 109 < Grжх. Prж < 6 1010. Переходный режим отличается неустойчивостью процесса течения и теплоотдачи и, как следствие, большим разбросом опытных точек. В некоторых случаях, как это имело место в опытах (рис. 10 -4), ламинарное течение сохраняется и при числах Grжх. Prж, больших 109. Развитое же турбулентное течение может наступить и при числах Grжх. Prж, меньших 6 1010.

Переходная область течения имеет место на определенной длине стенки. В среднем теплоотдача при переходном режиме возрастает от значения, соответствующего ламинарному течению, до значения, соответствующего турбулентному движению жидкости. Наибольшее и наименьшее значения коэффициента теплоотдачи в переходной области можно определить соответственно по уравнениям (10 -15) и (10 -13). Изменение коэффициента теплоотдачи при подъемном свободном движении вдоль вертикальной стенки и связь этого изменения с характером движения показаны на рис. 10 -5.
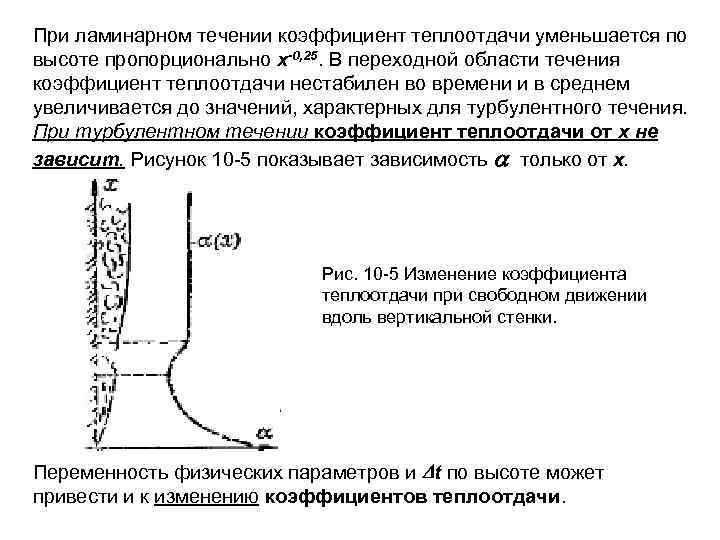
При ламинарном течении коэффициент теплоотдачи уменьшается по высоте пропорционально х-0, 25. В переходной области течения коэффициент теплоотдачи нестабилен во времени и в среднем увеличивается до значений, характерных для турбулентного течения. При турбулентном течении коэффициент теплоотдачи от х не зависит. Рисунок 10 -5 показывает зависимость только от х. Рис. 10 -5 Изменение коэффициента теплоотдачи при свободном движении вдоль вертикальной стенки. Переменность физических параметров и t по высоте может привести и к изменению коэффициентов теплоотдачи.

Теплоотдача при свободном движении около горизонтальной трубы Описанная картина свободного движения вдоль вертикальной стенки типична также и для свободного движения у наклонной стенки, шаров, горизонтальных круглых и овальных труб. Большое практическое значение имеет теплоотдача горизонтальных труб. Характер свободного движения около горячих горизонтальных труб представлен на рис. 10 -6. Рис. 10 -6, Свободное движение около горизонтальных труб.

При прочих равных условиях чем больше диаметр труб, тем вероятнее разрушение ламинарного течения. У труб малого диаметра разрушение ламинарного течения может происходить вдали от трубы. Для расчета средних коэффициентов теплоотдачи при свободном ламинарном движении около горизонтальных труб может быть использована формула (10. 16) В формуле (10. 16) за определяющую принята температура жидкости или газа вдали от трубы, в качестве определяющего размера берется диаметр трубы.
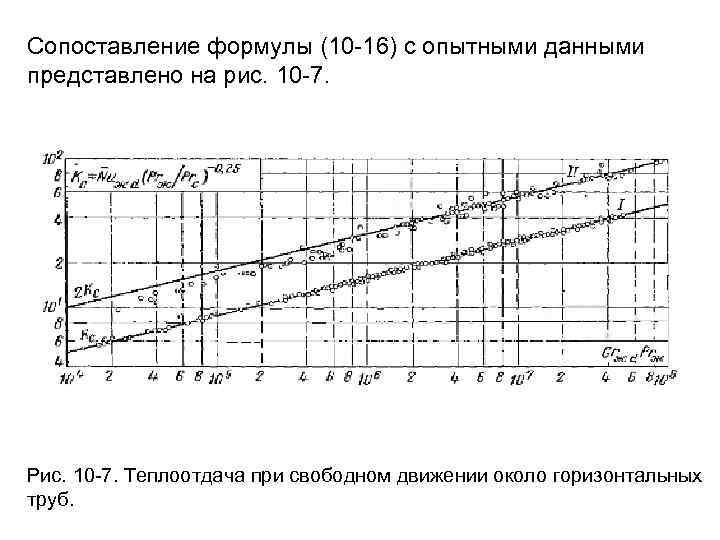
Сопоставление формулы (10 -16) с опытными данными представлено на рис. 10 -7. Рис. 10 -7. Теплоотдача при свободном движении около горизонтальных труб.

Теплоотдача при очень малых значениях комплекса Gr. Pr Было обнаружено, что для тонких проволочек (d=0, 2 2 мм) условия теплоотдачи своеобразны. Так как поверхность проволоки мала, то и количество передаваемой теплоты незначительно. При малых температурных напорах вокруг проволоки образуется неподвижная, пленка нагретого воздуха. Этот режим называется пленочным. Пленочный режим обнаружен при числах (Gr. СГPr. СГ) < 1, индексы «сг» и d показывают, что определяющими величинами являются температура t. СГ = 0, 5(tc+t 0) и диаметр d. При пленочном режиме Nu. СГ d = 0. 5, откуда = 0, 5( /d). Теплообмен осуществляется теплопроводностью. Пленочный режим весьма неустойчив.

В некоторых случаях уже при (Gr. СГPr. СГ) > 10 -3 появляются конвективные токи и число Нуссельта увеличивается при росте Gr. Pr. Этот режим является переходным от пленочного к ламинарному. Он имеет место при значениях (Gr. СГPr. СГ), примерно меньших 5 102. Наибольшее значение коэффициента теплоотдачи при переходном режиме описывается уравнением Наименьшее значение соответствует пленочному режиму.
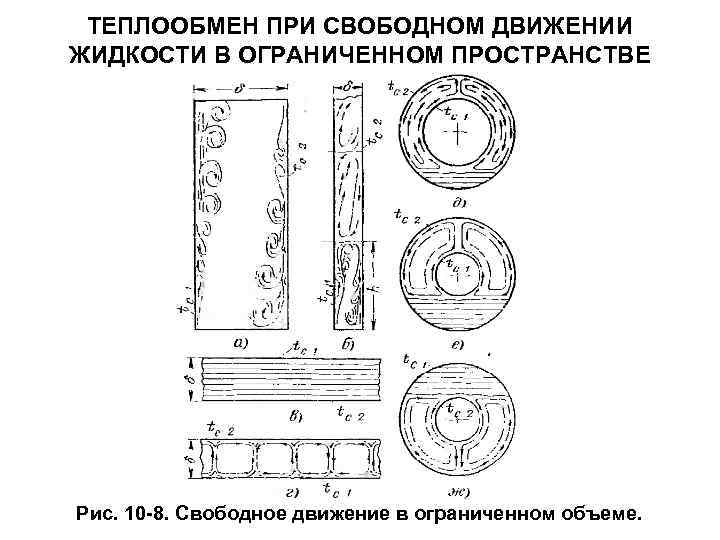
ТЕПЛООБМЕН ПРИ СВОБОДНОМ ДВИЖЕНИИ ЖИДКОСТИ В ОГРАНИЧЕННОМ ПРОСТРАНСТВЕ Рис. 10 -8. Свободное движение в ограниченном объеме.

Если объем жидкости невелик, то свободные движения, возникающие у других тел или частей данного тела, расположенных в этом объеме, могут сказываться на рассматриваемом течении. Разделить эти движения и рассматривать их по отдельности очень трудно, а порою и невозможно. Движение и теплоотдача зависят при этом как от рода жидкости, ее температуры и температурного напора, так и от формы и размеров пространства. В горизонтальных щелях, образованных двумя плоскими стенками, процесс определяется расположением нагретых и холодных поверхностей, расстоянием между ними и распределением температуры стенки. Течение жидкости может отсутствовать, если температура верхней стенки постоянна и больше температуры нижней (рис. 10 -8, в). Сказанное справедливо дли жидкостей, у которых плотность уменьшается с увеличением температуры. Неравномерность температуры стенок способствует появлению конвекции.

Если температура нижней стенки больше, чем температура верхней, то при определенных условиях в щели возникают конвекционные токи. Горячие частицы жидкости, имеющие меньшую плотность, стремятся вверх. В щели появляются восходящие потоки, чередующими между собой (рис. 10 -8, г). Поле потока, рассматриваемое сверху, имеет ячеистую структуру с более или менее правильными шестигранными ячейками. Внутри этих ячеек поток движется вверх, а по периферии ячеек он возвращается вниз. Такое течение имеет место примерно при Gr. Pr = 103 45 103. При Gr. Pr > 45 103 наступает развитое турбулентное течение, ячеистая структура может сохраниться только вблизи нижней стенки.

В вертикальных щелях в зависимости от расстоянии между стенками циркуляция жидкости может протекать по-разному. Если велико, то восходящий и нисходящий потоки движется без взаимных помех (рис. 10 -8, а). В этом случае движение имеет такой же характер, как и в неограниченном объеме. Если же мало, то вследствие взаимных помех возникают внутренние циркуляционные контуры (рис. 10 -8, 6). Высота контуров b определяется шириной щели, родом жидкости и интенсивностью процесса. Если Gr < 124 Рr-0, 2(0, 955 + Рr)l/ , где l — высота слоя, то перенос теплоты между стенками может быть вычислен по уравнениям теплопроводности. Отклонения имеют место только на концах щели на высоте, равной примерно .

В шаровых к горизонтальных цилиндрических прослойках циркуляция жидкости может протекать согласно схеме, изображенной на рис. 10 -8, д—ж. Течение развивается лишь в зоне, лежащей выше нижней кромки нагретой поверхности. Ниже этого уровня жидкость неподвижна. Если же нагрета внешняя цилиндрическая поверхность, то движение жидкости охватывает пространство, расположенное ниже верхней кромки холодной поверхности. При интенсивном теплообмене движением может быть охвачена вся жидкость. При практических расчетах обычно необходимо определить тепловой поток через слой жидкости. В расчетной практике принято заменять сложный процесс переноса теплоты через щели эквивалентным процессом теплопроводности.

Средняя плотность теплового потока q условно вычисляется по формулам теплопроводности. Для плоского слоя (10. 17) где dэкв—так называемый эквивалентный коэффициент теплопроводности, учитывающий перепос теплоты через щель как теплопроводностью, так и конвекцией. Отношение к = экв/ , где —коэффициент теплопроводности жидкости, характеризует влияние конвекции на перенос теплоты через щель. Величина к является функцией комплекса Gr. Pr. Зависимость к = f(Gr. Pr) представлена на рис. 10 -9. Для составления графика рис. 10 -9 использованы опытные данные для вертикальных и горизонтальных плоских щелей, кольцевых и сферических слоев, заполненных газом или капельной жидкостью.
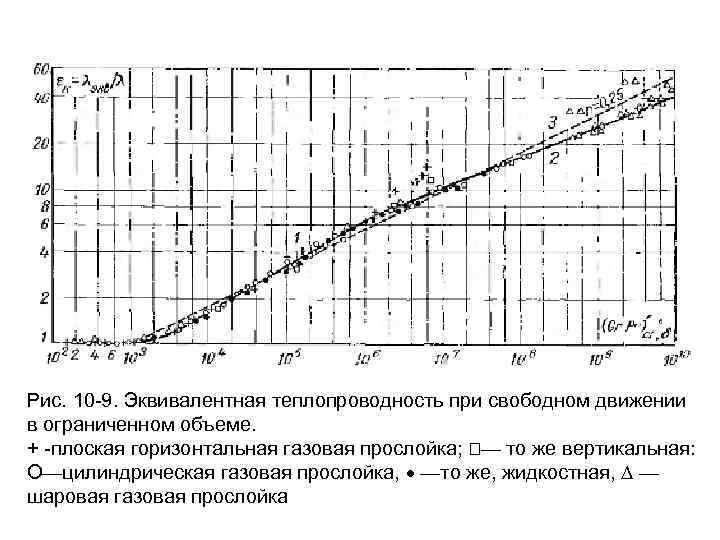
Рис. 10 -9. Эквивалентная теплопроводность при свободном движении в ограниченном объеме. + -плоская горизонтальная газовая прослойка; — то же вертикальная: О—цилиндрическая газовая прослойка, —то же, жидкостная, — шаровая газовая прослойка

При определении чисел подобия независимо от формы прослойки за определяющий размер принята ее толщина , а за определяющую температуру — средняя температура жидкости tcr=0. 5(tc 1 + tc 2). В случае малых значений аргумента (Gr. Pr)cr < 103, как следует из графика рис. 10 -9, к = 1 и э = , т. е. передача теплоты от горячей стенки к холодной осуществляется только теплопроводностью. При 103 < (Gr. Pr)cr < 106 (кривая 1) к =0, 105(Gr. Pr)0, 3 cr и при 106 < (Gr. Pr)cr < 1010 (кривая 2) к =0, 4(Gr. Pr)0, 2 cr

По Михееву, ввиду приближенности формул (10 -18) и (1019) для всей области значений аргументов (Gr. Pr)cr > 103 можно принять зависимость к =0, 18(Gr. Pr)0, 25 cr (10. 20) с некоторой погрешностью аппроксимирующей экспериментальные данные, представленные на графике рис. 10 -9 (кривая 3). Предложен ряд формул для расчета отдельных задач свободной конвекции в ограниченном объеме. При этом рассмотрена свободная конвекция у вертикального ряда горизонтальных труб, у вертикальной стенки с вертикальными ребрами, в горизонтальной щели, в горизонтальном цилиндрическом слое при различном положении внутреннего тепловыделяющего трубчатого элемента и другие практически важные задачи.
Теплопередача-14(СВОБОДНОМ ДВИЖЕНИИ ЖИДКОСТИ).ppt