Теплообмен при конденсации 1. Виды

Теплообмен при конденсации 1. Виды конденсации 2. Термическое сопротивление передаче тепл 3. Теплоотдача при конденсации неподвижного пара 3. 1. Понятие «неподвижный пар» 3. 2. Ламинарное течение пленки на вертикальной стенке 3. 3. Турбулентное течение пленки на вертикальной стенке 3. 4. Конденсация на горизонтальных трубах 4. Конденсация движущегося пара внутри труб 4. 1. Ламинарное течение пленки конденсата 4. 2. Турбулентное течение пленки конденсата

Виды конденсации. Конденсация представляет собой процесс перехода пара (газа) в жидкое или твердое состояние. Конденсация может происходить как в объеме пара, так и на охлаждаемой поверхности теплообмена. В первом случае образование конденсированной фазы может происходить самопроизвольно при значительном переохлаждении пара относительно температуры насыщения и на холодных жидких или твердых частицах, вводимых в пар. В большинстве областей техники и промышленности приходится иметь дело с конденсацией пара в жидкое состояние на охлаждаемых поверхностях теплообмена. Этот вариант и будем рассматривать. При этом будем полагать, что конденсирующийся пар не содержит примесей других паров или газов. Конденсация насыщенного или перегретого пара на твердой поверхности теплообмена происходит, если температура поверхности меньше температуры насыщения при данном давлении (Tw < Tнас; поэтому при конденсации перепад температур равен ΔT = T нас — Tw ). При этом на поверхности может образоваться пленка конденсата (пленочная конденсация) или происходит образование капель (капельная конденсация). Пленочная конденсация имеет место, если конденсат смачивает данную поверхность теплообмена при этом жидкая конденсированная фаза образуется на поверхности теплообмена в виде устойчивой пленки. Если же конденсат не смачивает поверхность, то происходит капельная конденсация.

Виды конденсации. Пленочная конденсация имеет место при соприкосновении водяного пара с чистой металлической поверхностью. Необходимо знать, что любая чистая поверхность металла постепенно покрывается загрязнениями и плохо смачивается, но с течением времени образуется оксидная пленка, на которой конденсация, рано или поздно, приобретает пленочный характер. Поэтому капельная конденсация особого интереса для инженеров не представляет, хотя при капельной конденсации теплообмен между паром и стенкой в 5 - 10 раз больше, чем при пленочной конденсации.

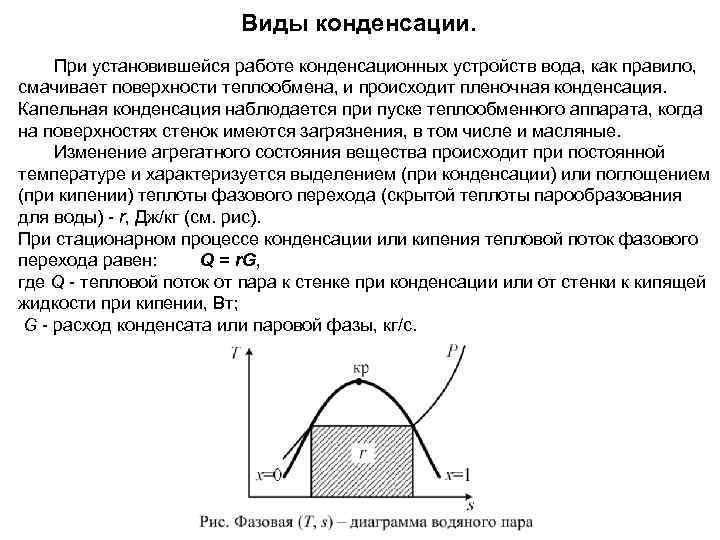
Виды конденсации. При установившейся работе конденсационных устройств вода, как правило, смачивает поверхности теплообмена, и происходит пленочная конденсация. Капельная конденсация наблюдается при пуске теплообменного аппарата, когда на поверхностях стенок имеются загрязнения, в том числе и масляные. Изменение агрегатного состояния вещества происходит при постоянной температуре и характеризуется выделением (при конденсации) или поглощением (при кипении) теплоты фазового перехода (скрытой теплоты парообразования для воды) - r, Дж/кг (см. рис). При стационарном процессе конденсации или кипения тепловой поток фазового перехода равен: Q = r. G, где Q - тепловой поток от пара к стенке при конденсации или от стенки к кипящей жидкости при кипении, Вт; G - расход конденсата или паровой фазы, кг/с.

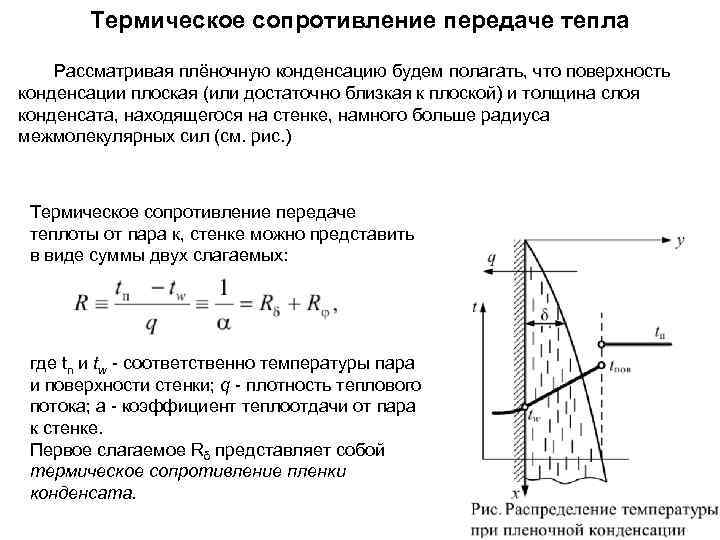
Термическое сопротивление передаче тепла Рассматривая плёночную конденсацию будем полагать, что поверхность конденсации плоская (или достаточно близкая к плоской) и толщина слоя конденсата, находящегося на стенке, намного больше радиуса действия межмолекулярных сил (см. рис. ) Термическое сопротивление передаче теплоты от пара к, стенке можно представить в виде суммы двух слагаемых: где tn и tw - соответственно температуры пара и поверхности стенки; q - плотность теплового потока; а - коэффициент теплоотдачи от пара к стенке. Первое слагаемое Rδ представляет собой термическое сопротивление пленки конденсата. 3. 2)

Термическое сопротивление передаче тепла Второе слагаемое Rφ, которое называется термическим сопротивлением на границе раздела фаз (межфазным термическим сопротивлением), не является термическим сопротивлением в его обычном понимании. Появление этого сопротивления обусловлено скачком температуры на границе раздела паровой и жидкой фаз. Наличие скачка температуры связано с особенностями движения молекул на поверхности раздела фаз. Это явление объясняет кинетическая теория материи. Для чистого водяного пара Rδ значительно больше Rφ и с достаточным приближением можно считать, что температурный скачок на границе раздела фаз отсутствует. Для других веществ данных о процессе конденсации недостаточно, поэтому для них допускается это же предположение. Термическое сопротивление пленки конденсата Rδ зависит от режима течения. Через ламинарно текущую пленку теплота переносится теплопровод- ностью, а через турбулентную – дополнительно конвекцией. Переход от ламинарного течения пленки к турбулентному определяют по значению числа Рейнольдса пленки. Для пленки локальное значение Re равно: где - средняя скорость течения пленки в рассматриваемом поперечном сечении; δ - толщина пленки конденсата в этом же сечении; νпл - коэффициент кинематический вязкости конденсата (пленки).

Термическое сопротивление передаче тепла Опытные данные показывают, что критическое число Рейнольдса может изменяться в пределах примерно от 60 до 500. Наиболее вероятным значением Reкр для случая конденсации практически неподвижного пара на вертикальной поверхности полагают значение Reкp = 400. В процессе конденсации расход конденсата тесно связан с тепловым потоком. При конденсации сухого насыщенного пара им отдается теплота фазового перехода r. Кроме того, поскольку температура поверхности стенки tw меньше температуры поверхности конденсата tпов, соприкасающейся с паром, стенке отдается и часть тепла конденсата, происходит переохлаждение конденсата. Но во многих практически важных случаях теплота переохлаждения пренебрежимо мала по сравнению с теплом фазового перехода, тогда Q = r. G. Расход конденсата в любом сечении движущейся пленки где lz -размер стенки в направлении, перпендикулярном движению плёнки. Отсюда На участке от x = 0 до x образовалось G (кг/с) конденсата и в единицу времени была передана теплота

Термическое сопротивление передаче тепла Отсюда и Таким образом, при названных условиях число Рейнольдса характеризует не только гидродинамику, но еще и интенсивность теплообмена. Приравняв правые части последних соотношений и продифференцировав левую и правую части полученного уравнения по x, окончательно получим следующее уравнение для местной плотности теплового потока:

Теплоотдача при конденсации неподвижного пара Понятие «неподвижный пар» Ламинарное течение жидкой пленки может сопровождаться волновым движением (см. рис. ). Возникшее под действием случайных возмущений волновое движение приводит к снижению эффективной толщины пленки конденсата, что в свою очередь вызывает уменьшение термического сопротивления и, следовательно, увеличение количества передаваемого при конденсации тепла. Из экспериментов следует, что волновой режим наблюдается при Re≈5. При конденсации пар не может быть абсолютно неподвижным. Объемы пара, конденсирующиеся у стенки, сейчас же восполняются новыми порциями пара, притекающими из основной массы последнего, поэтому пар всегда находится в движении. При конденсации неограниченного объема пара на плоской стенке пар перемещается нормально к ней. В большинстве случаев скорость этого перемещения не оказывает заметного динамического воздействия на пленку конденсата и поэтому пар может считаться неподвижным. В этом смысле и будет в дальнейшем употребляться термин «неподвижный пар» .

Теплоотдача при конденсации неподвижного пара Ламинарное течение пленки на вертикальной стенке На вертикальной стенке, температура поверхности которой всюду равна tw, конденсируется сухой насыщенный пар. Течение пленки имеет ламинарный характер. В результате интегрирования системы дифференциальных уравнений энергии и количества движения для плёнки можно получить: т. е. коэффициент теплоотдачи в определенной точке поверхности теплообмена прямо пропорционален коэффициенту теплопроводности и обратно пропорционален толщине пленки конденсата в этой точке. Толщина пленки конденсата будет зависеть от количества образовавшегося конденсата, или расхода конденсата в сечении. Количество конденсата, протекающего в единицу времени через поперечное сечение пленки при ширине последней, равной единице, определяется следующим выражением: За счет конденсации происходит прирост расхода.

Теплоотдача при конденсации неподвижного пара Ламинарное течение пленки на вертикальной стенке Рассматривая динамику движения плёнки и процесса конденсации получено выражение для толщины плёнки: Подставив значение δ в выражение , получим следующее уравнение для местного коэффициента теплоотдачи: Осреднение коэффициента теплоотдачи дает: где h - высота стенки. Это уравнение впервые получено Нуссельтом (1916 г. ).

Теплоотдача при конденсации неподвижного пара Ламинарное течение пленки на вертикальной стенке Из уравнений для δ и α можно выделить зависимость их от х: Характер этих зависимостей изображен на рис. Коэффициенты теплоотдачи уменьшаются с увеличением x или h , а толщина пленки, наоборот, увеличивается. Увеличением толщины пленки объясняется уменьшение коэффициентов теплоотдачи, так как термическое сопротивление при этом увеличивается.

Теплоотдача при конденсации неподвижного пара Ламинарное течение пленки на вертикальной стенке Как следует из уравнений для δ и α, их зависимость от температурного напора Δt аналогична зависимости этих величин от x и h. Решение Нуссельта не учитывает переменности физических параметров конденсата. Для учета зависимости коэффициентов теплопроводности и динамической вязкости от температуры правую часть формул Нуссельта нужно умножить на величину: где индексы « w » и «нас» означают, что данный коэффициент нужно выбирать соответственно по температуре поверхности стенки или температуре насыщения. Таким образом, для расчета средних коэффициентов теплоотдачи при конденсации неподвижного чистого пара на вертикальных поверхностях может быть использована формула где αN - коэффициент теплоотдачи, рассчитываемый по формуле Нуссельта при отнесении всех физических параметров конденсата к температуре насыщения; εv = Re 0, 04 - поправочный коэффициент на волновое течение пленки конденсата.

Теплоотдача при конденсации неподвижного пара Ламинарное течение пленки на вертикальной стенке Уравнение Нуссельта могут быть приведены к безразмерному виду. Выбрав в качестве определяемой величины получим: Где индекс «пл» обозначает, что в безразмерные величины входят физические параметры конденсата.

Теплоотдача при конденсации неподвижного пара Турбулентное течение пленки на вертикальной стенке При Re > 400 течение в пленке становится турбулентным. В верхней же части пленки, где Re < 400, течение продолжает оставаться ламинарным. На стенке будет иметь место смешанное течение конденсата. Локальный коэффициент теплоотдачи при пленочной конденсации и турбулентном движении плёнки может быть найден из выражения где: При расчете средней теплоотдачи турбулентного течения нужно учесть, что в верхней части стенки на ламинарном участке уже образовался определенный слой конденсата. В случае постоянных физических параметров Re ламинарного участка описывается уравнением Re = 0, 95 Z 0, 78. При этом Reкр = 400 соответствует:

Теплоотдача при конденсации неподвижного пара Турбулентное течение пленки на вертикальной стенке Полагая Reкр = 400 , Z кр = 2300, можно получить следующее уравнение: Это уравнение даёт среднее значение Re для вертикальной поверхности, на которой имеются ламинарный и турбулентный участки течения конденсата. Для учета зависимости физических параметров от температуры коэффициент 0, 024 в формуле должен быть умножен на поправку , где индексы «нас» и « w » означают, что число Прандтля конденсата выбирается соответственно по температурам насыщения и стенки. При этом все остальные физические параметры конденсата, входящие в уравнение, должны выбираться по температуре насыщения. С учетом сделанных замечаний формула числа Re для расчета среднего коэффициента теплоотдачи при конденсации неподвижного пара на вертикальной поверхности и смешанном течении пленки конденсата принимает следующий вид:

Теплоотдача при конденсации неподвижного пара Турбулентное течение пленки на вертикальной стенке Коэффициент теплоотдачи определяется следующей формулой: Определяющей температурой является температура насыщения tнас (исключая Prw), определяющим размером - высота стенки h. Все физические параметры берутся для конденсата.

Теплоотдача при конденсации неподвижного пара Конденсация на горизонтальных трубах Полученные ранее формулы справедливы при конденсации пара на вертикальных плоских стенках. В случае наклонной стенки в исходное уравнение вместо g необходимо ввести проекцию вектора ускорения свободного падения на ось Ox : где φ - угол, образованный направлением силы тяжести и осью координат Ox ориентированной по ходу течения пленки. В результате для наклонных стенок получается следующая формула: Выражение для расчета среднего коэффициента теплоотдачи при конденсации неподвижного пара на поверхности трубы примет вид: Эта формула отличается от формулы для вертикальной стенки тем, что коэффициент пропорциональности вместо 0, 943 равен 0, 728 и в качестве характерного размера вместо h вводится d.

Теплоотдача при конденсации движущегося пара внутри труб Если пар энергично движется сверху вниз и скорость движения пара совпадает по направлению со скоростью течения пленки конденсата, то коэффициент теплоотдачи увеличивается, так как толщина пленки становится меньше. При противоположном направлении скоростей коэффициент теплоотдачи уменьшается, так как толщина пленки вследствие трения становится больше. Если скорость восходящего пара становится выше определенного предела, то конденсатная пленка разрушается и оказывается сорванной с поверхности. Срыв пленки способствует интенсификации и возрастанию теплообмена. В зависимости от условий процесса пар может сконденсироваться в трубе как полностью, так и частично. При полной конденсации скорость пара на выходе из трубы равна нулю и выпар отсутствует. Если труба достаточно длинная и процесс конденсации достаточно интенсивен, то в концевой части трубы все ее сечение может быть заполнено конденсатом. Течение конденсата и пара может быть как ламинарным, так и турбулентным. На входе в трубу течение пара может быть турбулентным. По мере конденсации пара скорость его уменьшается и турбулентное течение может перейти в ламинарное. Если происходит полная конденсация, в конце участка конденсации аксиальная скорость пара будет равна нулю. В то же время расход конденсата вдоль трубы непрерывно увеличивается и течение конденсата может перейти в турбулентное. При определенных условиях может иметь место и срыв капель с поверхности пленки.

Теплоотдача при конденсации движущегося пара внутри труб Сочетание перечисленных условий делает задачу о теплообмене при конденсации пара в трубе очень сложной и затрудняет строгое и полное решение. К настоящему времени в этой области имеется много невыясненных вопросов. В частности, не ясны границы различных режимов. Многие исходные положения, используемые в теоретических решениях, недостаточно проверены опытами и т. п. Ввиду этого конкретные сведения о рассматриваемом процессе и расчетные рекомендации, которые в дальнейшем приводятся в дальнейшем довольно ограничены.

Теплоотдача при конденсации движущегося пара внутри труб Ламинарное течение пленки конденсата. Относительный коэффициент теплоотдачи может быть вычислен по формуле: где значения α неп вычисляются по формуле для практически неподвижного пара, конденсирующегося на вертикальной стенке. Числа Reпd изменялись в опытах от 1800 до 17000, этому соответствовала скорость пара от 3, 6 до 33, 5 м/с. Температурный напор изменялся от 8 до 60 К. При Ψ < 35 расчет можно вести по формулам для неподвижного пара.

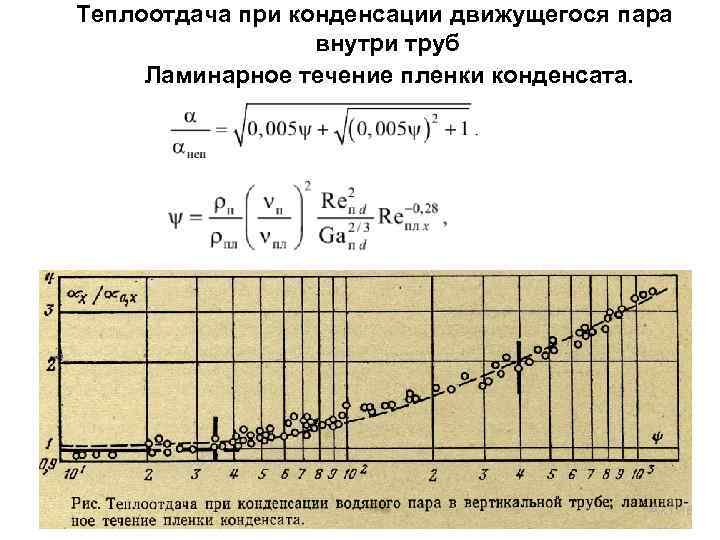
Теплоотдача при конденсации движущегося пара внутри труб Ламинарное течение пленки конденсата.

Теплоотдача при конденсации движущегося пара внутри труб Турбулентное течение пленки конденсата. Для турбулентного течения плёнки внутри труб была получена полуэмпирическая формула, описывающая местные коэффициенты теплоотдачи: где х -массовое расходное паросодержание в рассматриваемом сечении. Среднее значение коэффициентов теплоотдачи для режима неполной конденсации пара из пароводяной смеси определяется формулой: где х1 и х2 - массовые расходные паросодержания во входном и выходном сечении рассматриваемого участка трубы: G - массовый расход пара; Gсм - массовый расход парожидкостной смеси. Для стальных труб С = 0, 024 , для латунных С = 0, 026 , для медных С = 0, 032.

Теплоотдача при конденсации движущегося пара внутри труб Турбулентное течение пленки конденсата. Все физические параметры в формулах выбираются по температуре насыщения. Индексы «пл» и «п» обозначают, что данная величина является физическим параметром соответственно пленки конденсата и пара. Очень сложен процесс теплоотдачи при конденсации в горизонтальных трубах слабо движущегося пара, когда необходимо учитывать и силы тяжести, и силы трения. Эта задача приближенно решалась в некоторых работах. Полученные формулы достаточно сложны, так как приходится учитывать то обстоятельство, что конденсат течет как вдоль трубы, так и по ее окружности. При этом режимы течения пара и конденсата на различных участках трубы могут быть неодинаковыми. В то же время отсутствуют данные для определения границ участков с различными режимами течения пленки. Все эти особенности процесса существенно затрудняют получение точных зависимостей.

Теплоотдача при конденсации движущегося пара на горизонтальных трубах Теплоотдача при конденсации движущегося пара на горизонтальной трубе (течение пара сверху вниз) может быть рассчитана по формуле для ламинарного течения конденсата где - средний коэффициент теплоотдачи при конденсации неподвижного пара (см. выше); - число Фруда; wп - скорость набегающего на трубу пара; d -наружный диаметр трубы; g - ускорение свободного падения; K - число Кутателадзе; ΔT = Тнас- Tw - температурный напор; г 1/2

Теплоотдача при конденсации движущегося пара на пучке горизонтальных труб Процессы конденсации на наружной поверхности одиночной горизонтальной трубы, а также труб, собранных в пучок, различны. В случае чистого пара различие обусловлено двумя факторами: уменьшением скорости пара при его движении в пучке из-за частичной конденсации и за счет последовательного стекания конденсата с трубы на трубу. Уменьшение скорости пара по мере его продвижения через пучок приводит к уменьшению теплоотдачи при возрастании номера ряда. Конденсат стекает с трубы отдельными каплями или струйками (см. рис. ). Капли, попадая на нижележащую трубу, с одной стороны, временно утолщают пленку в месте падения, растекаясь затем по поверхности, с другой - возмущают течение пленки, что может способствовать появлению волнового или даже турбулентного режима движения. Места отрыва капель все время перемещаются вдоль трубы. Это перемещение усиливается, если труба имеет хотя бы небольшой наклон. В этом случае волнообразная утолщенная пленка передвигается вдоль нижней части трубы.

Теплоотдача при конденсации движущегося пара на пучке горизонтальных труб При очень больших скоростях пара капли могут уноситься паром, только частично попадая на другие трубы. Чем выше скорость капли, тем больше количества движения она может передать при падении на пленку. Описанный характер перемещения конденсата с трубы на трубу приводит к тому, что некоторое увеличение термического сопротивления за счет утолщения слоя конденсата может в значительной степени компенсироваться возникающими при этом возмущениями. При конденсации водяного пара на горизонтальных трубных пучках, обтекаемых сверху вниз чистым водяным паром, значения коэффициента теплоотдачи по рядам труб можно определить по следующей приближенной методике: 1). производится последовательный расчет количества пара ΔGп конденсирующегося на трубках каждого ряда, расхода пара Gп и коэффициента теплоотдачи αn по рядам. При этом Здесь Fn - площадь поверхности теплообмена рассматриваемого ряда труб; w 1 и wn - скорости потока пара перед первым и n-м рядами;

Теплоотдача при конденсации движущегося пара на пучке горизонтальных труб 2). Определяются поправки на влияние стекания конденсата: - суммарное количество конденсата, стекающего по n-й трубе; ΔGn - количество конденсата, образующегося на n-й трубе; 3). Значение коэффициента теплоотдачи для n-го ряда с учетом влияния скорости пара и стекания конденсата определяется как Средний коэффициент теплоотдачи для всего трубного пучка где Fi - площадь поверхности теплообмена отдельных труб; F - общая площадь поверхности теплообмена. Если все трубы в пучке одинаковые, то средний коэффициент теплоотдачи

Теплоотдача при конденсации движущегося пара на пучке горизонтальных труб Описанный выше способ расчёта очень трудоёмок. Расчёт существенно упрощается, если предположить, что температурный напор и давление пара не изменяется по высоте трубного пучка. Для этих условий получена приближённая формула для среднего по всему пучку коэффициента теплоотдачи : где: n - число рядов труб по высоте коридорного пучка или половина числа рядов труб по высоте шахматного пучка; ε=(GBX—GBb. IX)/GBX — степень конденсации пара; здесь Gвх и Gвых— массовые расходы пара на входе и на выходе из пучка; - коэффициент теплоотдачи, вычисленный по формуле Нуссельта: Если пар конденсируется полностью, то есть Gвых = 0, ε=1, тогда:

Влияние неконденсирующихся газов в паре Если в водяном паре присутствуют неконденсирующиеся газы (например, воздух), то теплоотдача резко снижается. В этом случае воздух на поверхности пленки конденсата создает воздушную прослойку, препятствующую конденсации пара (см. рис. ). Экспериментально получено, что присутствие в паре 1% воздуха уменьшает теплоотдачу приблизительно в два раза. Поэтому воздух необходимо удалять из теплообменных аппаратов.

Упражнения 1. Найти переданное количество теплоты и количество образовавшегося конденсата на одиночной горизонтальной трубе диаметром d = 16 мм и длиной l = 1, 5 м при конденсации на ней сухого насыщенного пара, рн = 4 к. Па. Температура поверхности трубы Тст =291 К. Конденсация пленочная, течение пленки конденсата ламинарное. 2. Определить местный (х = 3 м) коэффициент теплоотдачи к вертикальной стенке шириной 1 м от стекающей по ней пленки конденсата водяного пара. Количество образующегося конденсата на единице длины стенки Мτ = 1, 2 кг/с. Параметры пара рн = 4, 24 к. Па, Тн = 303 К. Физические свойства пара считать постоянными и определить их по температуре насыщения.