ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ.ppt
- Количество слайдов: 41

ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ

Особенности теплообмена излучением. Основные понятия и определения Все нагретые материальные объекты излучают энергию в окружающее пространство с помощью электромагнитных волн, которые излучаются атомами вещества и распространяются в пространстве прямолинейно. Затем это излучение поглощается другими атомами в других областях пространства и т. д. Помимо волновых свойств, излучение обладает также корпускулярными свойствами, т. е. лучистая энергия испускается и поглощается дискретно отдельными квантами энергии или фотонами. Таким образом, излучение имеет двойственный характер, т. к. обладает свойствами непрерывности поля электромагнитных волн и свойствами дискретности, типичными для фотонов.

Таким образом, излучение характеризуется длиной волны и частотой колебаний Скорость кванта определяется по формуле: Распределение энергии по длинам волн и частот в спектре излучающего тела связано с температурой и физической структурой тела. Тело, обладающее спектром, соответствующим максимально возможному тепловому излучению при заданной температуре, называется абсолютно черным. Абсолютно черное тело полностью поглощает любое падающее на него тепловое излучение. Свойства реальных тел в большей или меньшей степени отличаются от свойств абсолютно черного тела. Распределение энергии излучения абсолютно черного тела соответствует условиям термодинамического равновесия и однозначно определяется его температурой. В связи с этим излучение абсолютно черного тела называют также равновесным излучением.

Моделью абсолютно черного тела является бесконечно малое отверстие в равномерно прогретой полости. Многократное отражение луча, попавшего через малое отверстие, обеспечивает практически его полное поглощение независимо от отражательной способности внутренних поверхностей полости. Спектр излучения практически всех твердых тел является непрерывным, газов – прерывистым, т. е. излучение селективно. У твердых тел поглощение и излучение происходит в тонком пограничном слое. Это позволяет использовать излучательные характеристики непосредственно геометрическим поверхностям тел. В общем случае поверхность тела частично поглощает, частично отражает и частично пропускает падающее из окружающего пространства тепловое излучение. Поглощенное излучение превращается в тепловую энергию тела, которая в виде лучистой энергии участвует в собственном излучении этого тела.

Энергия излучения, испускаемая в единицу времени по различным направлениям полупространства и соответствующая интервалу волн от до называется потоком монохроматического или спектрального излучения Суммарное излучение с поверхности тела по всем длинам волн спектра называется интегральным потоком излучения Интегральный поток, испускаемый с единицы поверхности, называется поверхностной плотностью потока интегрального излучения: – поток излучения, испускаемый элементарной площадкой

Тогда лучистый поток со всей поверхности: Если плотность потока интегрального излучения для всех элементов излучающего тела , то: Спектральная плотность потока излучения: Плотность потока излучения может изменяться в зависимости от направления излучения. Количество энергии, испускаемой в направлении , определяемом углом с нормалью к поверхности , единицей элементарной площадки в единицу времени в пределах единичного телесного угла называется угловой плотностью излучения.

Угловые плотности спектрального излучения определяются: и интегрального Отсюда: Количество лучистой энергии, испускаемой в направлении угла в единицу времени элементарной площадкой на плоскость, ортогональную к направлению излучения, называется интенсивностью (яркостью) излучения:

и - интенсивности спектрального и интегрального излучения Излучение, интенсивность которого одинакова по всем направлениям, называется изотропным. Если это излучение с поверхности твердого тела, то оно называется диффузным излучением. Излучение, обусловленное природой и температурой тела, называется собственным излучением. Количество энергии излучения, падающей на данное тело, обозначается

Поток поглощенного телом излучения – Собственная плотность потока поглощенной лучистой энергии определяется по формуле. - коэффициент поглощения телом излучения. Для абсолютно черного тела Тела, для которых спектральная поглощательная способность не зависит от длины волны, называются серыми телами. Для серых тел коэффициент поглощения При этом часть падающей энергии отражается или проходит через них. .

Часть энергии, которую поверхность отражает, носит название потока отраженного излучения. Соответственно, плотность потока отраженного излучения определяется: - коэффициент отражения. При поверхность называется зеркальной. Если имеет место диффузное отражение, то энергия отражается равномерно по всем направлениям. Часть энергии, которая проходит сквозь тело, называется плотностью потока пропускаемого излучения. Соответственно, плотность потока отраженного излучения определяется: - коэффициент пропускания. Тела, которые пропускают всю падающую энергию, называются диатермичными.

Суммарная плотность потоков собственного и излучения, испускаемого поверхностью тела, плотностью эффективного излучения: отраженного называется Эффективное излучение зависит от формы, размера и относительного расположения тел в пространстве. Для тела, участвующего в радиационном теплообмене с другими телами, согласно закону сохранения энергии: Если разделить на , то:

Лучистый теплообмен между телами определяется потоком результирующего излучения. Результирующее излучение представляет собой разность между лучистым потоком, получаемым телом, и лучистым потоком, передаваемым в окружающую среду. Плотность результирующего излучения может быть определена из теплового баланса относительно поверхности, расположенной внутри тела вблизи его поверхности: Плотность результирующего излучения может быть определена также из баланса относительно воображаемой поверхности, расположенной вне тела, но вблизи его поверхности: В общем случае плотность потока результирующего излучения определяется разностью встречных потоков излучения, падающих на условную поверхность, расположенную между телами:

Учитывая, что: Получим: При , тогда: Для абсолютно черного тела и , т. е. эффективное излучение вырождается в собственное.

Законы теплового излучения Энергия кванта определяется формулой: – постоянная Планка, Дж∙с. Интенсивность монохроматического излучения, отнесенная к данной частоте, определяется следующим образом: – формула Планка. Дж/К – постоянная Больцмана.

Через длину волны: и учитывая, что : Соответственно: и

Соответственно: Если Вт∙м 2 , , м∙К, то закон Планка Если энергия кванта существенно меньше энергии теплового движения. Тогда формула Планка переходит в закон Релея-Джинса

Если , то Закон Планка примет вид формулы Вина: Из формулы Планка получен закон Стефана-Больцмана путем интегрирования по частоте от 0 до Анализ показывает, что излучение свойственно всем телам при : любой температуре независимо от температурного состояния окружающих тел. Основной особенностью излучения является существенная зависимость от как для абсолютно черного тела, так и для серых тел. В последнем случае энергия излучения меньше: – степень черноты теплового излучения. Величина зависит от природы тела, температуры, состояния поверхности и определяется экспериментальным путем.

Исходя из Закона Планка, получен закон смещения Вина: м∙К Т. е. положение максимума Для Солнца через однозначно определяется температурой. =0, 4*10 -4 м определена температура 60000 С Законы теплового излучения получены применительно к идеальному абсолютно черному телу и термодинамическому равновесию. Рассмотрим закон Кирхгофа – один из основных законов теплового излучения, который устанавливает количественную связь между энергиями излучения и поглощения поверхностями серых и абсолютно черных тел. В излучающей системе, состоящей из относительно большого замкнутого объема с теплоизолированными стенками и помещенных в него тел. В условиях термодинамического равновесия для каждого из этих тел энергия излучения равна поглощенной энергии:

и т. д. Откуда получаем закон Кирхгофа: Согласно этому закону отношение энергии излучения к энергии поглощения не зависит от природы тел и равно энергии излучения абсолютно черного тела при той же температуре. Зависимости справедливы и для спектральных величин:

Степень черноты, соответствующая направленному излучению Закон Ламберта устанавливает следующее: поток излучения абсолютно черного тела в данном направлении пропорционален потоку излучения в направлении нормали и косинусу угла между ними: – угловые плотности потоков интегрального излучения соответственно в направлении, определенным углом и в направлении нормали к поверхности. Из закона Ламберта
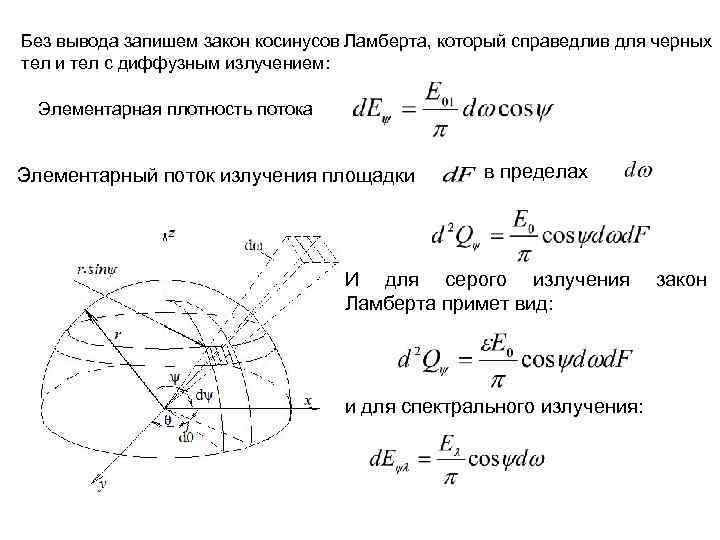
Без вывода запишем закон косинусов Ламберта, который справедлив для черных тел и тел с диффузным излучением: Элементарная плотность потока Элементарный поток излучения площадки : в пределах И для серого излучения Ламберта примет вид: и для спектрального излучения: закон

Однако многие тела не подчиняются этому закону. Например, полированные металлы имеют яркость излучения при превышающую яркость в направлении нормали к поверхности. При увеличении яркость уменьшается до нуля. Если для данного тела известна зависимости яркости интегрального или спектрального излучения, то в общем случае поверхностная плотность собственного излучения определяется из соотношений:
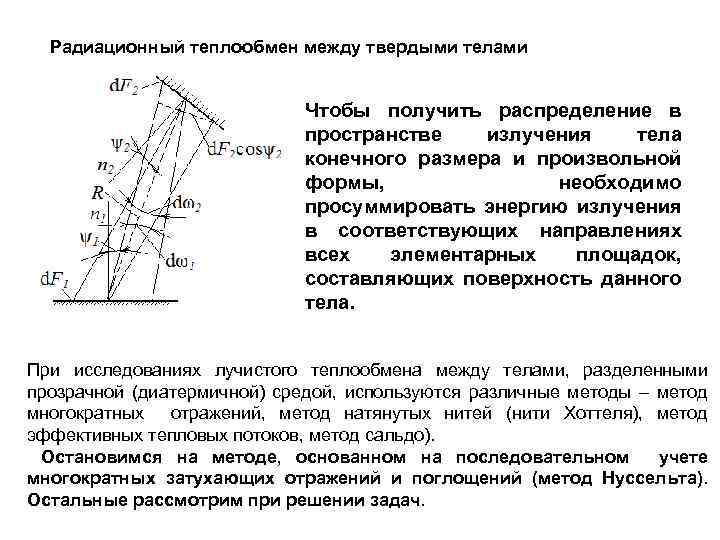
Радиационный теплообмен между твердыми телами Чтобы получить распределение в пространстве излучения тела конечного размера и произвольной формы, необходимо просуммировать энергию излучения в соответствующих направлениях всех элементарных площадок, составляющих поверхность данного тела. При исследованиях лучистого теплообмена между телами, разделенными прозрачной (диатермичной) средой, используются различные методы – метод многократных отражений, метод натянутых нитей (нити Хоттеля), метод эффективных тепловых потоков, метод сальдо). Остановимся на методе, основанном на последовательном учете многократных затухающих отражений и поглощений (метод Нуссельта). Остальные рассмотрим при решении задач.

Пусть коэффициенты поглощения теплового излучения (степени черноты) не зависят от температуры и координат точек на поверхностях, температуры и плотности потоков собственного излучения вдоль поверхностей не меняются. Определим плотность потока результирующего излучения. Собственное излучение первого тела: Это собственное излучение первой поверхности полностью попадает на вторую поверхность и поглощается в количестве: Остальная часть отражается второй поверхностью обратно в направлении первой поверхности:

Из этой части первая поверхность поглощает: и отражает на вторую поверхность: И т. д. Аналогично такую процедуру можно выполнить и для второй поверхности. Для расчета результирующего потока можно использовать выражение: Или в конечном итоге: Учитывая справедливое для серых тел равенство

Метод наглядный, но наиболее громоздкий. Другие методы (метод эффективных тепловых потоков, метод сальдо) рассмотрим на практике. Рассмотрим два тела, разделенных диатермичной средой, причем одно тело находится в полости другого. Тело 1 –выпуклое, а тело 2 – вогнутое. Геометрические размеры тел коэффициенты поглощения коэффициенты излучения температуры поверхностей > Тогда результирующий поток излучения: – средний угловой коэффициент излучения. характеризует часть потока эффективного излучения, который попадает со второго тела на первое по отношению к полному потоку эффективного излучения второго тела. Угловой коэффициент , т. к. энергия, излучаемая первым телом, полностью попадает на второе тело. Угловой коэффициент
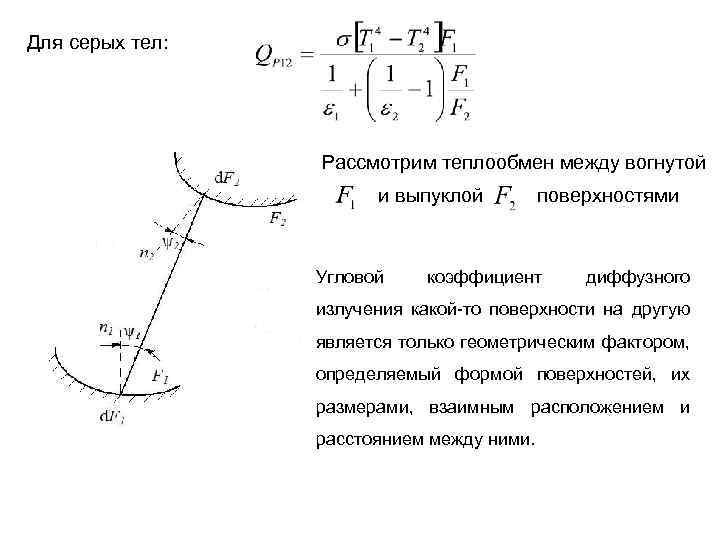
Для серых тел: Рассмотрим теплообмен между вогнутой и выпуклой Угловой поверхностями коэффициент диффузного излучения какой-то поверхности на другую является только геометрическим фактором, определяемый формой поверхностей, их размерами, взаимным расположением и расстоянием между ними.

Поток эффективного излучения поверхности саму на себя можно записать в виде (плотность потока эффективного излучения по поверхности принимается постоянной): Без вывода запишем применительно к телу с вогнутой поверхностью Угловой коэффициент зависит от геометрических особенностей: – для собственного диффузного излучения тела при одинаковой плотности этого излучения по всей поверхности и одинаковой температуре; – для отраженного диффузного излучения при одинаковой плотности потока этого излучения по всей его поверхности. Угловые коэффициенты излучения определяются различными методами – интегрирования, поточной алгебры, натянутых нитей Хоттеля, интегрирования по контуру, дифференцирования известных угловых коэффициентов, сферы единичного радиуса Нуссельта. Также используются графические и экспериментальные методы. В результате применения этих методов получен ряд формул для многих случаев взаимного расположения тел.

Свойства угловых коэффициентов излучения и взаимных поверхностей с постоянной плотностью потока излучения Свойство 1 (из закона Кирхгофа). Если два тела находятся во взаимном лучистом теплообмене, то их взаимные поверхности равны, а угловые коэффициенты обратно пропорциональны поверхностям тел: Свойство 2. Если ^ телом с вогнутой поверхностью и окружающей средой происходит лучистый теплообмен, то угловой коэффициент этой поверхности в окружающую среду меньше 1 на величину углового коэффициента излучения этой поверхности самой на себя. Поток излучения поверхности После преобразований получим следующие соотношения: Для тел с плоской или выпуклой поверхностью

Свойство 3. Если между одним из тел замкнутой системы происходит радиационный теплообмен со всеми другими телами, то сумма угловых коэффициентов переноса энергии излучения этого тела на все тела, образующие замкнутую систему, равна 1, а сумма всех взаимных поверхностей тел равна поверхности этого тела (рис. ). Общий поток излучения поверхности можно представить в виде: Отсюда получаем: Или:

Свойство 4 Если между телом 1 с поверхностью и телом 2 с поверхностью происходит радиационный теплообмен и оба тела образуют замкнутую систему, то величина углового коэффициента излучения поверхности на поверхность и величина взаимной поверхности не зависят от формы и протяженности поверхности (рис. вспомог. поверхности):

Свойство 5. Если величина углового коэффициента излучения с любого элемента поверхности на поверхность сохраняет свое значение постоянным, то справедливы следующие соотношения: Свойство 6. Если тело полностью закрывается другими телами от тела то справедливо следующее соотношение:

Теплообмен между газом и поверхностью твердого тела Газы обладают способностью излучать и поглощать лучистую энергию. Для разных газов она различна. Излучение обычных одно- и двухатомных газов (азота, кислорода, водорода и т. п. ), за исключением некоторых (например, оксид углерода) настолько незначительно, что в инженерных расчетах эти газы обычно рассматривают как абсолютно прозрачные (диатермичные). Значительной способностью излучать и поглощать лучистую энергию обладают многоатомные газы, в частности диоксид углерода, водяной пар и т. д. При наличии в среде раскаленных частиц сажи газовая среда становится светящейся (такую среду называют пламенем или факелом). Излучение и поглощение газов имеет объемный характер, в связи с этим существенную роль играют размеры и форма излучающего слоя, распределение температуры. Спектры излучения и поглощения газов носят селективный характер, т. е. процессы излучения и поглощения происходят лишь внутри ряда дискретных полос спектра; при других длинах (частотах) волн газ ведет себя как прозрачная диатермическая среда. Эти особенности излучения и поглощения энергии в газах осложняют расчеты лучистого теплообмена.

Рассмотрим одномерную задачу, причем среду будем считать только поглощающей, т. е. пренебрегаем собственным излучением среды. Тогда по мере прохождения через среду потока излучения его интенсивность будет уменьшаться. Обозначим заданную интенсивность излучения источника на граничной поверхности Считаем, что интенсивность излучения по длинам волн при прохождении в направлении через слой среды толщиной : уменьшается пропорционально этой интенсивности и величине – спектральная поглощательная способность среды, характеризующая относительное изменение интенсивности излучения на единицу длины луча. Это уравнение является основным законом переноса поглощающей среде. Его можно представить в виде: (1) энергии в

Коэффициент поглощения среды определяется по отношению лучистой энергии, поглощенной в слое , к энергии, падающей на границу этого слоя: Пусть – оптическая толщина слоя среды. Если поглощательная постоянная, то: способность среды – величина Тогда (1) приобретает вид закона Бугера: При термодинамическом Кирхгофа: равновесии на основании закона

При прохождении тепловых лучей в поглощающей среде поглощенная энергия переходит сначала в теплоту и снова излучается средой. Таким образом, интенсивность излучения вдоль луча будет уменьшаться вследствие поглощения и увеличиваться за счет собственного излучения. Тогда: С другой стороны согласно закону Кирхгофа для поглощающей среды – объемна плотность потока излучения, т. е. лучистый поток, испускаемый единицей объема среды в единицу времени по всем направлениям в пределах пространственного угла.

Интегрирование уравнения: 1 -й член – интенсивность падающего излучения, 2 -й - собственного Эта зависимость определяет яркость излучения, как функцию координат точки, направления излучения и длины волны в поглощающей и излучающей среде. В частном случае постоянных значений температуры, оптических свойств среды и давления (для газов) это уравнение имеет вид: Или: Интенсивность излучения, поступающего в среду на границе определяется свойствами поверхности, ограничивающей среду. Для диффузной поверхности: спектральные коэффициенты излучения и отражения стенки;

– спектральная интенсивность излучения абсолютно черного тела при температуре стенки; – то же для потока, падающего на стенку. После преобразований: Если среда характеризуется еще и рассеянием лучистой энергии (ослабляющая среда), то в полученные зависимости вместо коэффициента вводится коэффициент ослабления среды Одним из важнейших параметров излучения является оптическая толщина среды

Величину интерпретируют как глубину проникновения фотонов или как среднюю длину свободного пробега фотонов. В случае длина свободного пробега фотонов значительно больше характеристик линейного размера системы. Плотность собственного углерода и водяного пара: интегрального излучения для диоксида - парциальное давление Несмотря на то, что излучение газа существенно отличается от закона Стефана-Больцмана, многие авторы для практических расчетов рекомендуют пользоваться этим законом. Расчетное уравнение теплообмена излучением между газом и стенками канала имеет следующий вид:

Эффективный коэффициент черноты стенок канала, учитывающий внутреннее излучение газа, определяется по формуле: - поверхностная плотность лучистого потока соответственно газа и абсолютно черного тела; – поправка, учитывающая взаимное поглощение энергии излучения газами (для дымовых газов составляет 2 -4%, поэтому ею обычно пренебрегают); - степень черноты газа, диоксида углерода и водяных паров при средней температуре стенок канала; - поправочный коэффициент, учитывающий более сильное влияние парциального давления по сравнению с влиянием толщины слоя газа;

- средняя температура соответственно газа и стенок канала, К. Эффективная толщина слоя газа приблизительно может быть определена: – объем газа; – площадь поверхности оболочки; – поправочный коэффициент ( =0, 9).
ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ.ppt