ТЕПЛОМАССООБМЕН Конвективный теплообмен Лекция 7 2017 год

ТЕПЛОМАССООБМЕН Конвективный теплообмен Лекция № 7 2017 год

План • 1. Закон Ньютона и коэффициент теплоотдачи. • 2. Теплоотдача при свободном движении. – А. ) Теплоотдача при свободном движении неограниченном пространстве. – Б. ) Теплоотдача при свободном движении ограниченном пространстве. в в

1. Закон Ньютона и коэффициент теплоотдачи Второй вид теплообмена – конвекция – происходит в газах и жидкостях и состоит в том, что перенос теплоты осуществляется перемещающимися в пространстве объемами среды.

• Передача теплоты конвекцией всегда связана с теплопроводностью. • Совместный процесс конвекции и теплопроводности называется конвективным теплообменном. • В большинстве теплообменных аппаратах давление постоянно, и газы и жидкости подчиняются общим законам движения и передачи теплоты.

• При малых скоростях движения жидкостей имеет место ламинарный (спокойный, струйчатый) режим движения, характеризующийся Re < 2200÷ 2400. • При больших скоростях – турбулентный (возмущенный, вихревой) режим движения, для которого Re > 8000÷ 10000. • Промежуточный режим движения жидкости называется переходным.

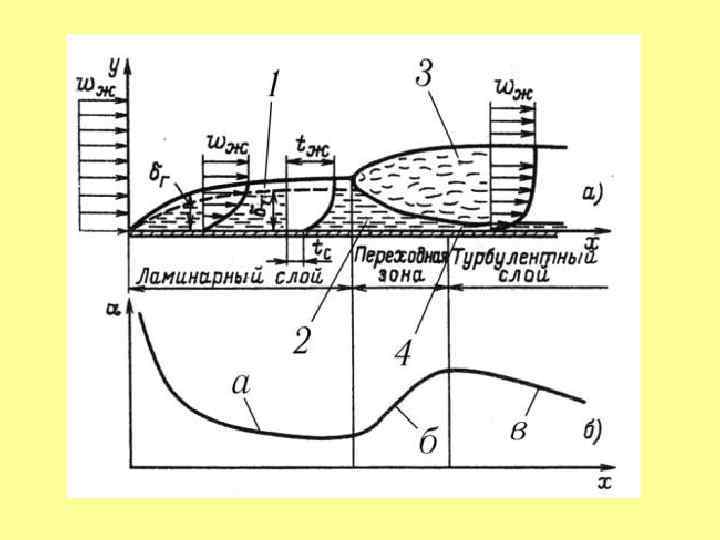
• В покоящейся жидкости теплообмен осуществляется теплопроводностью, если толщина слоя не велика и конвекция не развита. • С началом движения жидкости по мере перехода от малых скоростей к все большим и от ламинарного режима к турбулентному роль теплопроводности уменьшается, а конвекции – растет.

• Свободное движение жидкости (газа) совершается под действием разности плотностей нагретых и холодных ее частей. • Вынужденное движение жидкости происходит под действием внешних сил, создающихся насосами, компрессорами, вентиляторами и т. п.

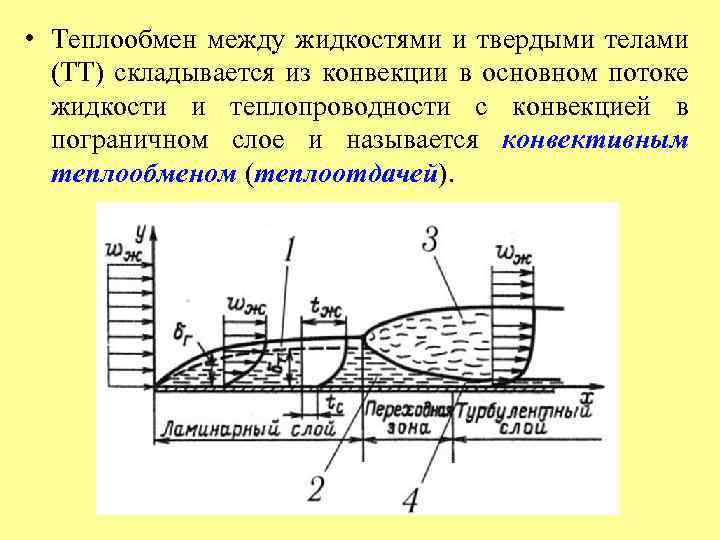
• Теплообмен между жидкостями и твердыми телами (ТТ) складывается из конвекции в основном потоке жидкости и теплопроводности с конвекцией в пограничном слое и называется конвективным теплообменом (теплоотдачей).

• Вследствие небольшой величины коэффициента теплопроводности для капельных жидкостей и газов интенсивность теплоотдачи определяется в основном теплопроводностью через пограничный слой, зависящий от его толщины δп. • Вблизи поверхности ТТ изменяются: Ø как скорость жидкости – от ω = 0 (частиц, «прилипших» к поверхности ТТ) до ω = ω0 (свободного потока); Ø так и температура – от температуры поверхности (стенки) t=tс до температуры свободного потока (температуры торможения) t=t 0.

• Поскольку расстояния по сечению потока между экстремальными значениями ω и t не совпадают, различают гидродинамический и тепловой пограничные слои. Ø δг – толщина гидродинамического пограничного слоя. Ø δт – толщина теплового пограничного слоя. • Для газов и горячей воды толщины пограничных слоев (гидродинамический и тепловой) практически равны δг=δт=δп.

Ø При малых скоростях гидродинамический слой является ламинарным, затем, пройдя через переходный режим, он становится турбулентным. Ø В процессе этих переходов теплообмен становится более интенсивным (интенсифицируется). Ø При турбулентном режиме у поверхности ТТ сохраняется тонкий ламинарный подслой, через который теплота передается теплопроводностью и температура изменяется более резко.

• Т. о. , казалось бы, тепловой поток при теплоотдаче можно определять по уравнению Фурье • Из-за трудности измерения толщины пограничного слоя δп и перепада температур в пограничном слое Δtп = t 0 – tcт такая возможность исключается.

Ø Для вычисления формулами теплового потока пользуются

Ø Полное количество переносимой теплоты где α – коэффициент конвективной теплоотдачи, Вт/(м 2·К); t 1 – температура теплоносителя, °C; t 2 – температура поверхности стенки, °C; F – поверхность соприкосновения теплоносителя со стенкой, м 2; R – сопротивление теплоотдаче.

Ø Соотношение носит название закона конвективной теплоотдачи Ньютона. Ø Закон Ньютона: Количество передаваемой теплоты пропорционально падению температуры, площади поверхности ТТ F, участвующей в теплообмене, и времени теплообмена τ. Ø Коэффициент теплоотдачи α представляет собой количества тепла, передаваемой в единицу времени единице поверхности тела при разности температур между поверхностью ТТ и жидкостью в 1 К.

• В отличии от коэффициента теплопроводности коэффициент теплоотдачи α – очень сложная величина: λ α = ƒ ( ω, λ, ν, ρ, cp, β, tж, tст, Ф, l 1, l 2, l 3…. ), где Ф – форма стенки. Ø Коэффициент теплоотдачи зависит от многих факторов, влияющих на теплопроводность пограничного слоя, так и от факторов, влияющих на конвекцию жидкости: формы и размера поверхности ТТ, ее состояния, физических свойств и параметров состояния жидкости, режима движения жидкости и т. д.

• Для определения коэффициента теплоотдачи α для различных случаев конвективного теплообмена предложено несколько эмпирических формул, имеющих ограниченную область применения. • Лучшие результаты дает определение величины коэффициента теплоотдачи α на основе эксперимента с использованием критериев подобия – безразмерных соотношений параметров, характеризующих физический процесс.

Критерий Рейнольдса Re – критерий режима движения жидкости. Критерий Грасгофа Gr – критерий подъемной силы. Критерий Нуссельта теплоотдачи. Nu – критерий Критерий Прандтля Pr физических свойств жидкости. – критерий

Число Рейнольдса • где ω – скорость потока (м/с); d – эквивалентный диаметр канала; ν – коэффициент кинематической вязкости (м 2/с). • Критерий Рейнольдса характеризует гидродинамический режим движения, являясь мерой отношения сил инерции и вязкости. • При малых силах инерции и больших силах вязкости движение ламинарное, в противоположном случае турбулентное.

Число Грасгофа где расширения (К-1); – коэффициент объемного – для идеального газа; Δt – разность температур в двух точках системы потока и стенки (К). Если ρж и ρс – плотности жидкости в двух точках системы, то

Число Грасгофа • Критерий Грасгофа характеризует гидродинамическое подобие при свободном движении жидкости. • Критерий Грасгофа отражает соотношение между подъемной силой, заставляющей всплывать нагретые частицы теплоносителя (архимедова сила), и силой вязкостного трения, препятствующей подъему этих частиц. • Чем Gr выше, тем свободное движение интенсивнее.

Число Нуссельта • где α – коэффициент конвективной теплоотдачи (Вт/м 2·К). • Критерий Нуссельта характеризует отношение между интенсивностью теплоотдачи и температурным полем в пограничном слое потока. • Чем Nu выше, тем интенсивнее конвективного теплообмена. процесс

Число Прандтля • где ср – теплоемкость жидкости при постоянном давлении (Дж/кг·К); • λ – коэффициент теплопроводности жидкости; • a – коэффициент температуропроводности (м 2/с). • Критерий Прандтля характеризует физические свойства жидкости и способность распространения тепла в жидкости. Ø Для газов Pr = 0, 67÷ 1, 0 и зависит только от атомности; Ø для жидкостей Pr = 1, 0÷ 2500; Ø для жидких металлов Pr = 0, 005÷ 0, 05.

• В общем случае конвективного теплообмена критериальная зависимость имеет вид • При стационарном режиме критерий Фурье Fo мал, тогда: • При вынужденном движении жидкости влияние свободной конвекции незначительно и критерий Грасгофа Gr можно не учитывать: • Если жидкость движется свободно, то исключается число Рейнольдса Re:

2. Теплоотдача при свободном движении происходит при обогреве помещений, в котельных агрегатах с естественной циркуляцией пароводяной смеси и т. д. Различают теплоотдачу в неограниченном пространстве. ограниченном и

А. ) Теплоотдача при свободном движении в неограниченном пространстве Свободное движение возникает в связи с изменением плотности жидкости от нагревания. Свободная конвекция имеет место у нагретых стен печей, трубопроводов, у батарей центрального отопления, в холодильниках при охлаждении продуктов и др.

• Свободный теплообмен возникает в неравномерно нагретом газе или жидкости, находящихся как в ограниченном, так и в неограниченном пространстве. • Если тело имеет более высокую температуру, чем окружающая среда, то слои жидкости, нагреваясь от тела, становятся легче и под действием подъемной силы поднимаются вверх, а на их место поступают из окружающего пространства более холодные слои. Поэтому возникает свободное движение. Рассмотрим свободный теплообмен в неограниченном пространстве у вертикальной плиты (стены) или трубы.

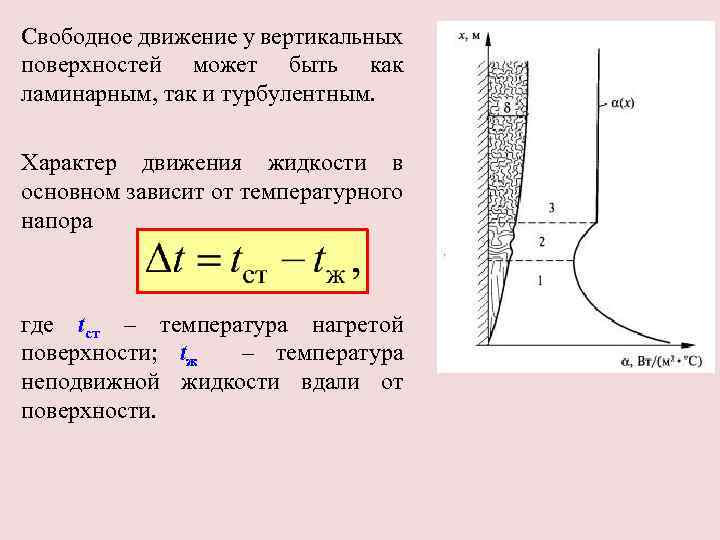
Свободное движение у вертикальных поверхностей может быть как ламинарным, так и турбулентным. Характер движения жидкости в основном зависит от температурного напора где tст – температура нагретой поверхности; tж – температура неподвижной жидкости вдали от поверхности.

• При малых значениях температурного напора вдоль всей поверхности наблюдается ламинарное движение жидкости. • При больших температурных напорах преобладает турбулентный режим движения. • Основное значение для свободного движения жидкости имеет длина поверхности, вдоль которой происходит теплообмен.

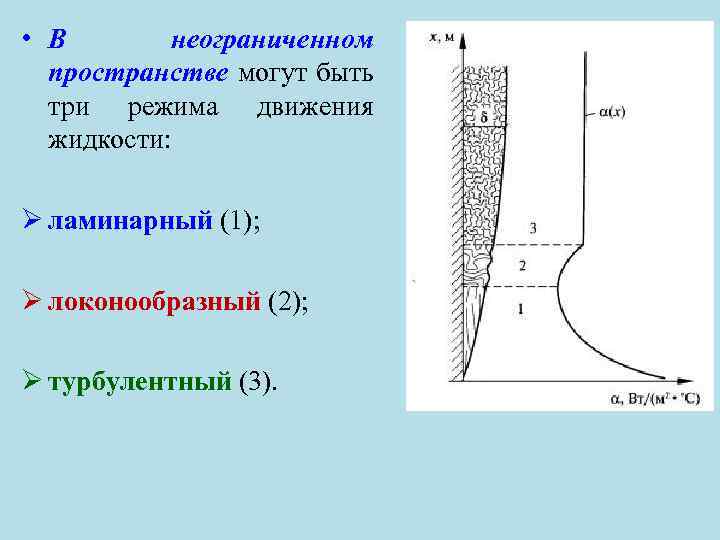
• В неограниченном пространстве могут быть три режима движения жидкости: Ø ламинарный (1); Ø локонообразный (2); Ø турбулентный (3).

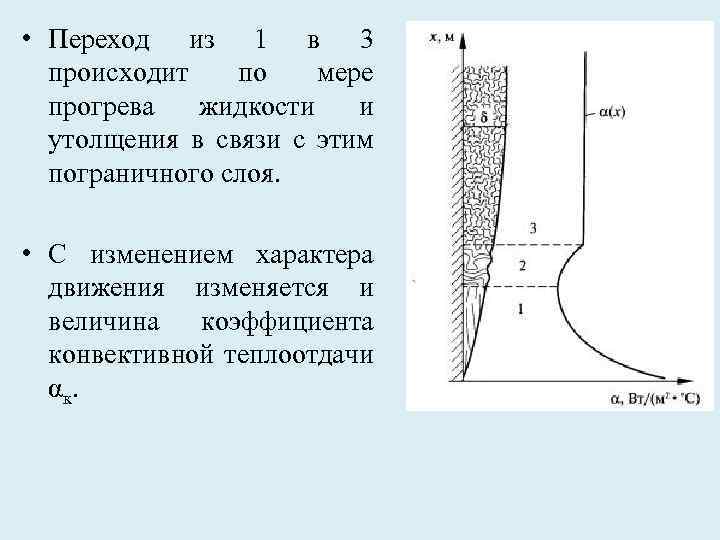
• Переход из 1 в 3 происходит по мере прогрева жидкости и утолщения в связи с этим пограничного слоя. • С изменением характера движения изменяется и величина коэффициента конвективной теплоотдачи α к.

• На участке 1 вследствие увеличения толщины пограничного слоя термическое сопротивление его возрастает и коэффициент конвективной теплоотдачи αк убывает. • На участке 2 коэффициент конвективной теплоотдачи αк резко возрастает, достигая постоянного значения при турбулентном режиме (участок 3). • Таким образом, при теплоотдаче в неограниченном пространстве главную роль играет протяженность поверхности, а не ее геометрическая форма.

• Для определения коэффициента конвективной теплоотдачи αк пользуются критериальным уравнением М. А. Михеева (1)

Значение констант C и m в уравнении в зависимости от Gr. Pr Константа С m 10 -3 – 5·102 – 2·107 – 1013 1, 18 0, 54 0, 135 0, 125 0, 250 0, 333

• Уравнение (1) применимо для тел любой формы при омывании их любыми капельными жидкостями и газами при Pr ≥ 0, 7. • За определяющую температуру принимают среднюю температуру пограничного слоя • За определяющий геометрический размер: Ø для труб и шаров – их диаметр; Ø для плоских стенок – их высоту.

• На рисунке показан характер свободного движение жидкости около горячих горизонтальных труб. • У труб малого диаметра восходящий поток сохраняет ламинарный режим даже вдали от трубы. • При большом диаметре переход в турбулентный режим может происходить в пределах поверхности самой трубы.

Б. ) Теплоотдача при свободном движении в ограниченном пространстве Теплоотдача в замкнутом ограниченном пространстве не может развиваться свободно, поэтому условия теплообмена в этом случае определяются формой и размерами пространства. Рассчитывать такой теплообмен очень трудно.

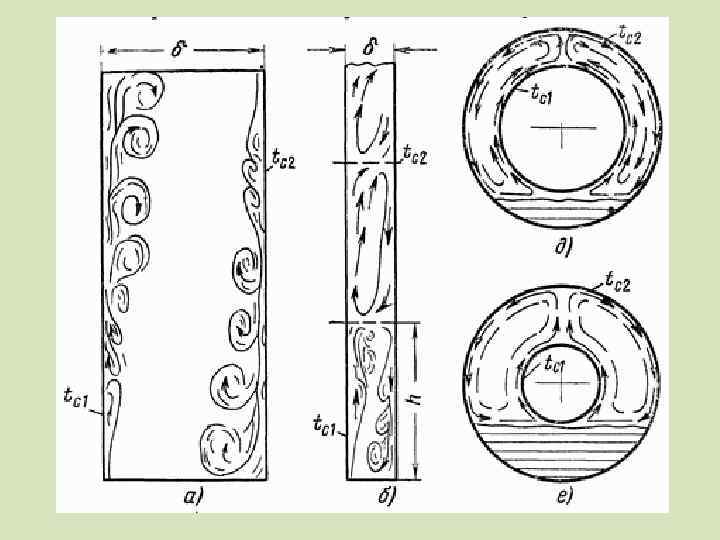
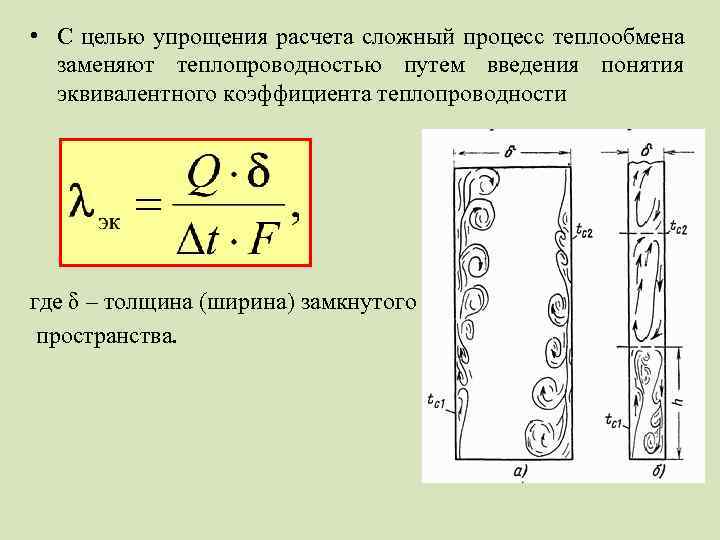
• С целью упрощения расчета сложный процесс теплообмена заменяют теплопроводностью путем введения понятия эквивалентного коэффициента теплопроводности где δ – толщина (ширина) замкнутого пространства.

• Влияние конвекции учитывается коэффициентом конвекции, представляющим собой отношение эквивалентного коэффициента теплопроводности λэк к обычному коэффициенту теплопроводности λ той же среды при средней ее температуре: • В приближенных расчетах при (Grж. Prж) > 103 принимают: • После этого определяются и