теория выход задачи Справочник Скрещивающиеся прямые —

теория выход задачи Справочник

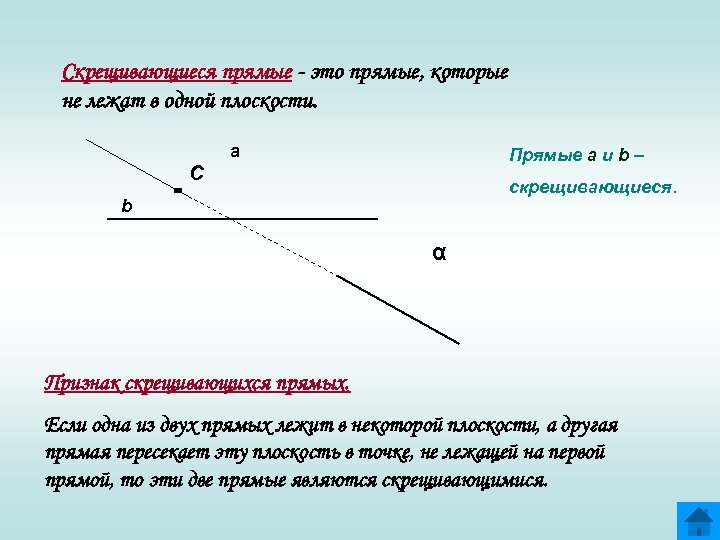Скрещивающиеся прямые - это прямые, которые не лежат в одной плоскости. a Прямые a и b – С скрещивающиеся. b α Признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти две прямые являются скрещивающимися.

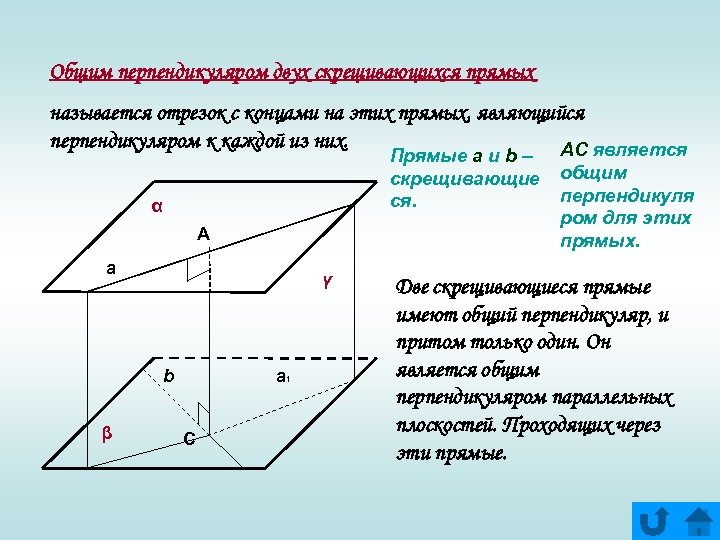Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них. AC является Прямые a и b – скрещивающие ся. α А a γ b β a 1 С общим перпендикуля ром для этих прямых. Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром параллельных плоскостей. Проходящих через эти прямые.

Определим расстояние между скрещивающимися прямыми Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Оно равно расстоянию между параллельными плоскостями, проходящими через эти прямые. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

Основные способы решения задач на нахождение расстояний между скрещивающимися прямыми. 1 способ 2 способ 3 способ 4 способ

1 способ Нахождение длины общего перпендикуляра двух скрещивающихся прямых, т. е. отрезка с концами на этих прямых и перпендикулярного обеим.

Способ 2 Нахождение расстояния от одной из скрещивающихся прямых до параллельной ей плоскости, проходящей через другую прямую.

Способ 3 Нахождение расстояния между двумя параллельными плоскостями, проходящими через заданные скрещивающиеся прямые.

Способ 4 Нахождение расстояния от точки, - являющейся проекцией одной из скрещивающихся прямых на перпендикулярную ей плоскость – до проекции другой прямой на ту же самую плоскость.

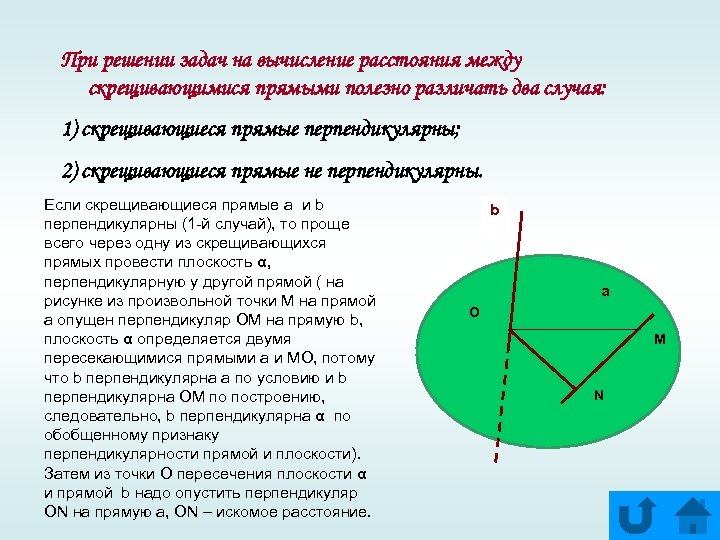При решении задач на вычисление расстояния между скрещивающимися прямыми полезно различать два случая: 1) скрещивающиеся прямые перпендикулярны; 2) скрещивающиеся прямые не перпендикулярны. Если скрещивающиеся прямые a и b перпендикулярны (1 -й случай), то проще всего через одну из скрещивающихся прямых провести плоскость α, перпендикулярную у другой прямой ( на рисунке из произвольной точки М на прямой a опущен перпендикуляр ОМ на прямую b, плоскость α определяется двумя пересекающимися прямыми a и МО, потому что b перпендикулярна а по условию и b перпендикулярна ОМ по построению, следовательно, b перпендикулярна α по обобщенному признаку перпендикулярности прямой и плоскости). Затем из точки О пересечения плоскости α и прямой b надо опустить перпендикуляр ОN на прямую а, ОN – искомое расстояние. b a О M N

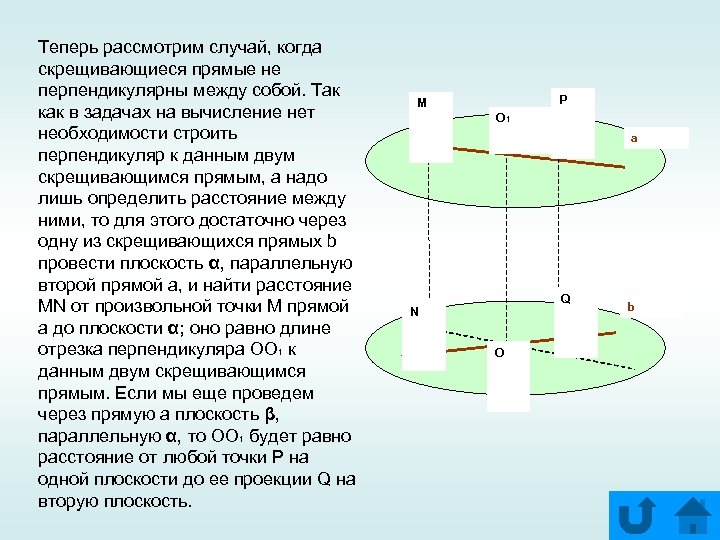Теперь рассмотрим случай, когда скрещивающиеся прямые не перпендикулярны между собой. Так как в задачах на вычисление нет необходимости строить перпендикуляр к данным двум скрещивающимся прямым, а надо лишь определить расстояние между ними, то для этого достаточно через одну из скрещивающихся прямых b провести плоскость α, параллельную второй прямой а, и найти расстояние MN от произвольной точки М прямой а до плоскости α; оно равно длине отрезка перпендикуляра ОО 1 к данным двум скрещивающимся прямым. Если мы еще проведем через прямую а плоскость β, параллельную α, то ОО 1 будет равно расстояние от любой точки Р на одной плоскости до ее проекции Q на вторую плоскость. P M O 1 a Q N O b

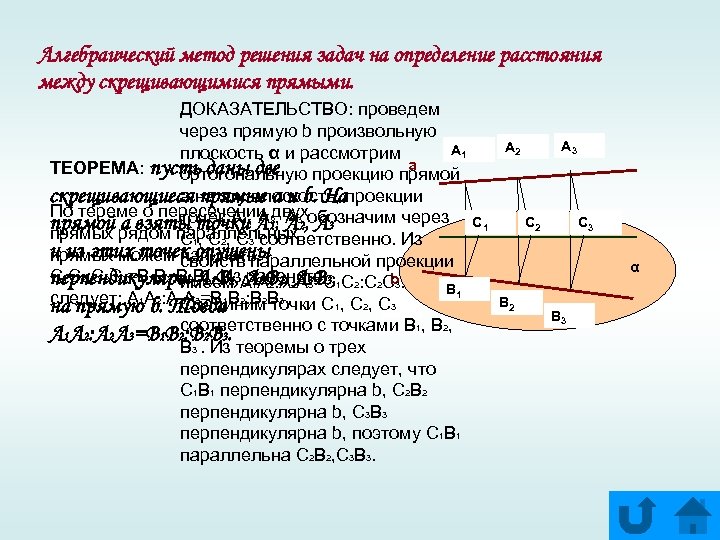Алгебраический метод решения задач на определение расстояния между скрещивающимися прямыми. ДОКАЗАТЕЛЬСТВО: проведем через прямую b произвольную A 1 плоскость α и рассмотрим a ТЕОРЕМА: пусть даны две ортогональную проекцию прямой а прямые a и b. На скрещивающиеся на эту плоскость; проекции По тереме о пересечении 2 двухобозначим через точек А 1 А , А прямой рядом параллельных32, А 3 а взяты точки, А 1, А прямых С 1, С 2, С 3 соответственно. Из и из этих точек опущены прямых можем свойств параллельной проекции написать: С 1 С 2: С 2 С 3=В 1 В 2: В 2 В 3. В 1, А 1 А 2: А 2 А 3 В 3, 1 С 2: С 2 С 3. b перпендикуляры А 1 Из А 2 В 2, А 3=С имеем равенств B 1 следует: А 1 А 2: А 2 Соединим В 3 А 3=В 1 В 2: В 2 точки С 1, С 2, С 3 на прямую b. Тогда А 1 А 2: А 2 А 3=В 1 В 2 соответственно с точками В 1, В 2, : В 2 В 3. Из теоремы о трех перпендикулярах следует, что C 1 B 1 перпендикулярна b, C 2 B 2 перпендикулярна b, C 3 B 3 перпендикулярна b, поэтому C 1 B 1 параллельна C 2 B 2, C 3 B 3. A 3 A 2 C 1 C 2 C 3 α B 2 B 3

Рассмотрим другие методы решения задач на определение расстояния между скрещивающимися прямыми. Один из этих методов базируется на теореме об объеме треугольной пирамиды. Итак, объем вписанной ДОКАЗАТЕЛЬСТВО: из Объем пирамиды равен: треугольной пирамиды произвольной вершины (В 1) ТЕОРЕМА: объем треугольной составляет одну треть объема параллелепипеда ABCDA 1 B 1 C пирамиды равен одной шестой 1 D 1 описанного параллелепипеда, проведем диагонали B 1 A, B 1 D 1, произведениясходящихся в этойее Так как или после , длин двух любых B 1 C гранейпреобразования, вершине. Концы ребер скрещивающихся этих на диагоналей соединим между расстояние между ними и на синус собой. Получим пирамиду угла между ниминазывается. B 1 AD 1 C, которая (вписанной в параллелепипед. А основания этих пирамид равновелики и равны половине параллелепипед, наоборот, площади основания описанным вокруг этой параллелепипеда, а высоты их пирамиды ( его легко построить, равны высоте h проводя пары параллельных параллелепипеда), то плоскостей через противоположные ребра пирамиды). B 1 C 1 A 1 D 1 B C k A D

При решении задач на нахождение расстояния между скрещивающимися прямыми можно использовать особенности описанного параллелепипеда в зависимости от свойств вписанной треугольной пирамиды. Например, если в пирамиде два скрещивающихся ребра: А) равны, то у описанного параллелепипеда грани. В которых лежат эти ребра, будут прямоугольниками; Б) перпендикулярны, то соответствующие грани будут ромбами; В) равны и перпендикулярны, то соответствующие грани будут квадратами.

Для нахождения расстояния между скрещивающимися прямыми а и b можно использовать следующий план: 1. На одной из данных прямых, например на прямой b, выбираем некоторую точку W и строим плоскость α, определяемую прямой α и точкой W. 2. В плоскости α через точку W проводим прямую а 1║а. 3. Строим плоскость β, определяемую пересекающимися прямыми а 1 и b. Ясно, что так как прямая α параллельна прямой а 1 , то прямая α параллельна и плоскости β. Поэтому точки прямой а одинаково удалены от плоскости β. Расстояние от любой точки U прямой а до плоскости β равно расстоянию между скрещивающимися прямыми а и b. Таким образом, задача нахождения расстояния между скрещивающимися прямыми может быть сведена к задаче нахождения расстояния от точки до плоскости.

Список задач Задача 1 Задача 7 Задача 2 Задача 8 Задача 3 Задача 9 Задача 4 Задача 10 Задача 5 Задача 11 Задача 6 Задача 12

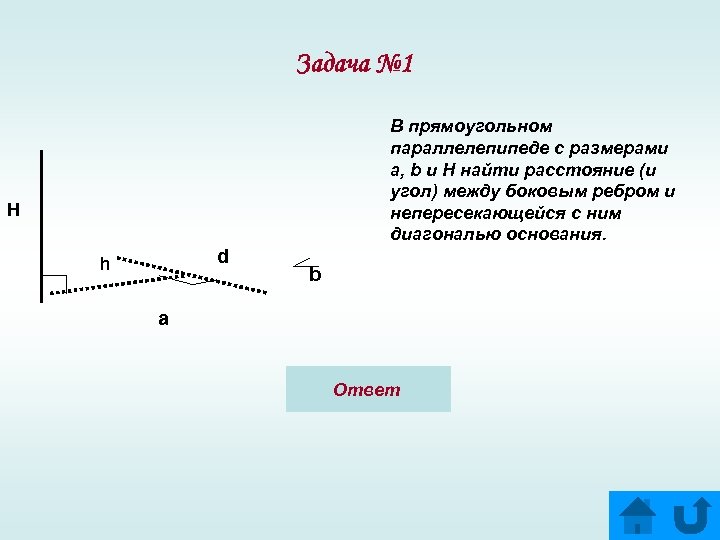Задача № 1 В прямоугольном параллелепипеде с размерами a, b и H найти расстояние (и угол) между боковым ребром и непересекающейся с ним диагональю основания. Н d h b a Ответ

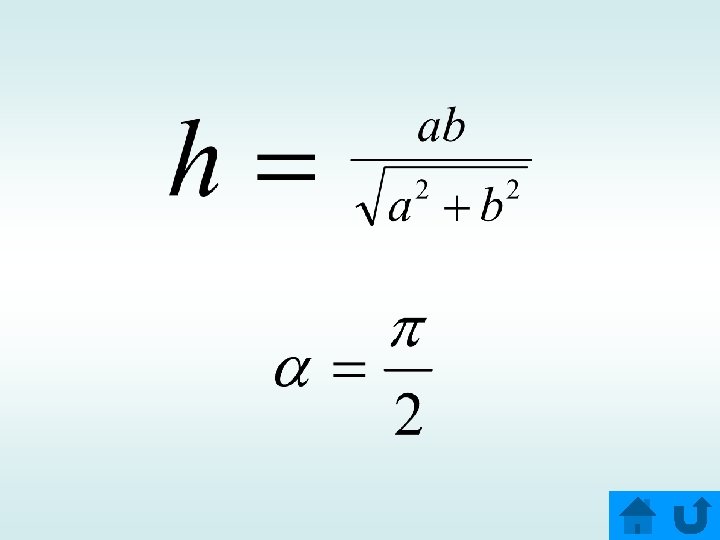
Задача № 2 В правильной четырехугольной пирамиде с боковым ребром L и стороной основания a найти расстояние и угол между апофемой и стороной основания, пересекающей боковую грань, содержащую эту апофему. L ha H k a2 hскр a Ответ

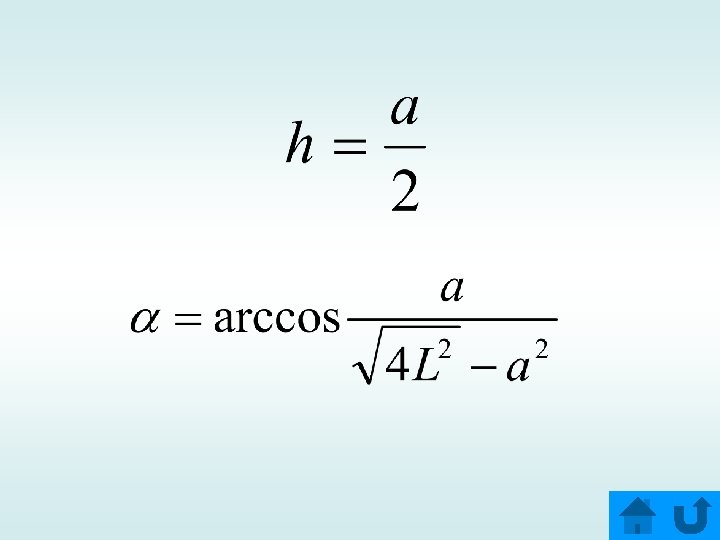
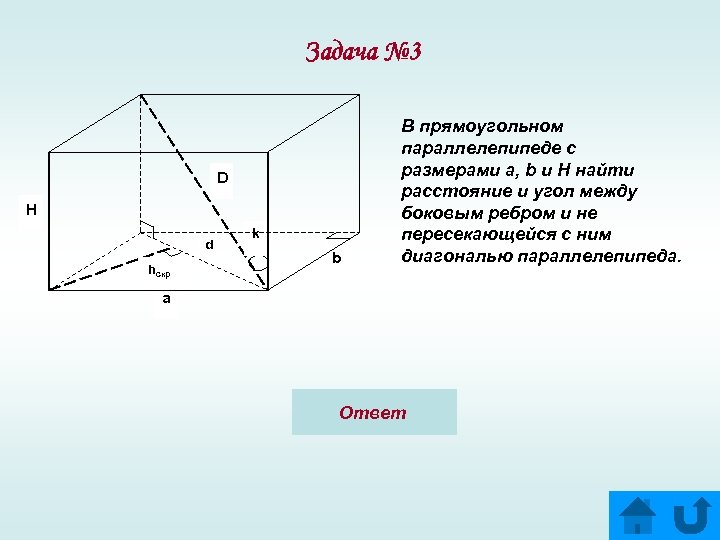Задача № 3 D H d hскр k b В прямоугольном параллелепипеде с размерами a, b и H найти расстояние и угол между боковым ребром и не пересекающейся с ним диагональю параллелепипеда. a Ответ

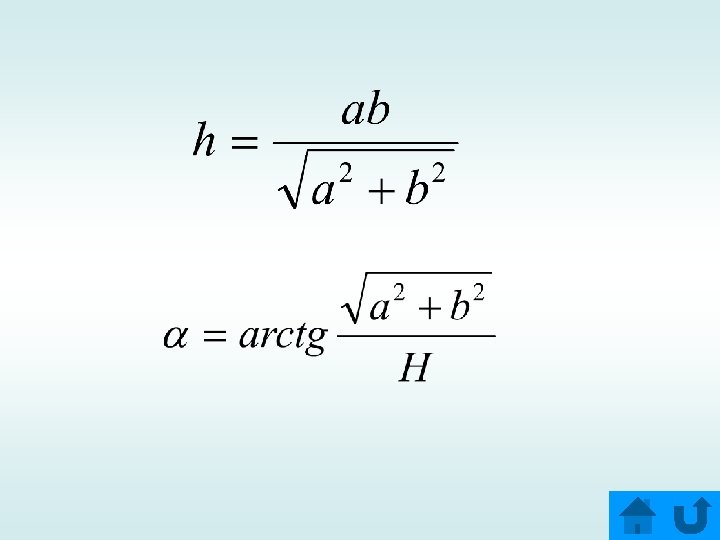
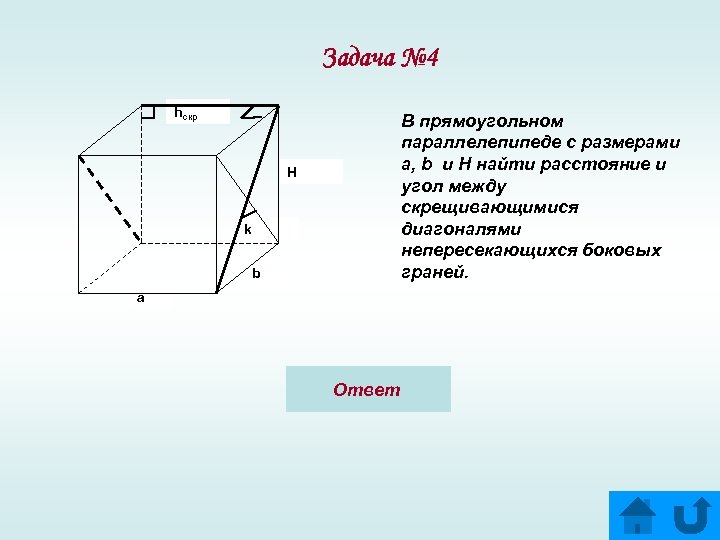Задача № 4 hскр В прямоугольном параллелепипеде с размерами a, b и H найти расстояние и угол между скрещивающимися диагоналями непересекающихся боковых граней. H k b a Ответ

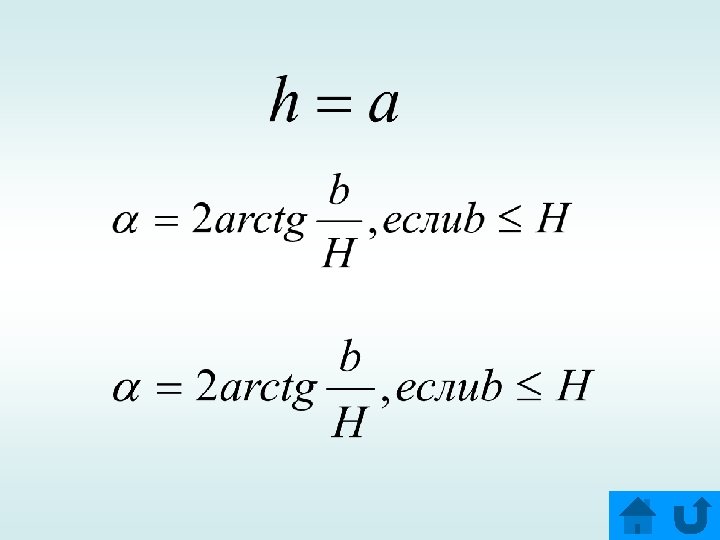
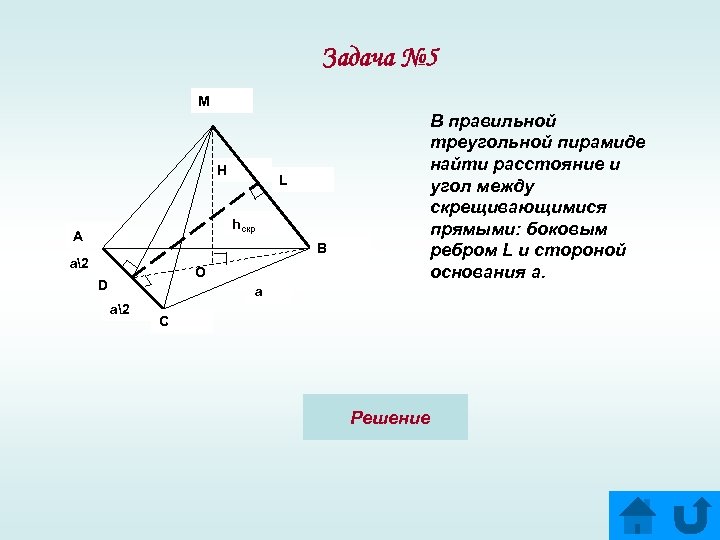Задача № 5 M H L hскр A B a2 O D В правильной треугольной пирамиде найти расстояние и угол между скрещивающимися прямыми: боковым ребром L и стороной основания а. a a2 C Решение

Решение к задачи № 5 Ответ:

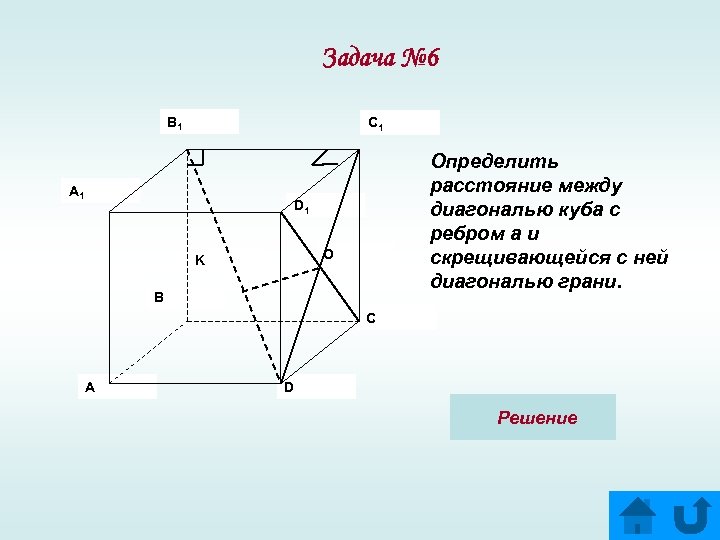Задача № 6 B 1 C 1 A 1 Определить расстояние между диагональю куба с ребром а и скрещивающейся с ней диагональю грани. D 1 O K B C A D Решение

Задача № 7 D 1 C 1 A 1 B 1 Е F Определить расстояние между скрещивающимися диагоналями смежных граней куба, ребро которого равно а. D C A B Решение

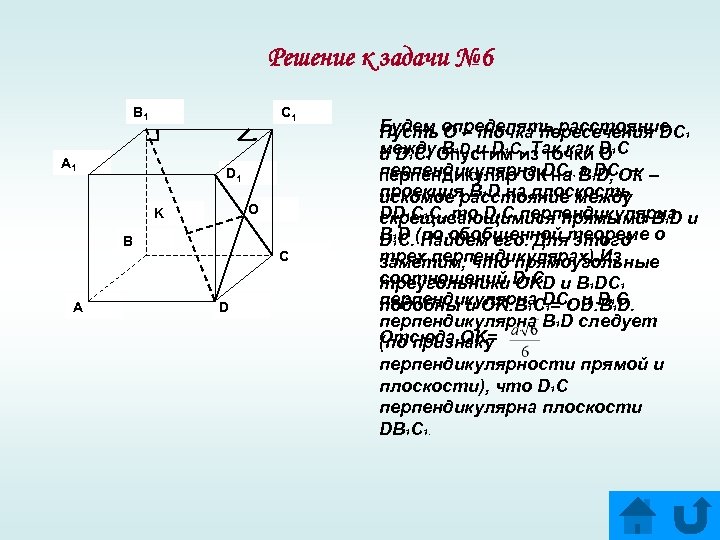Решение к задачи № 6 B 1 C 1 A 1 D 1 O K B A C D Будем определять расстояние 1 Пусть О – точка пересечения DC между B 1 D и D 1 C. Так как D 1 C и D 1 C. Опустим из точки О перпендикулярна DC 1, а DC 1 – перпендикуляр ОК на B 1 D, ОК – проекция B 1 D на плоскость искомое расстояние между DD 1 C 1 C, то D 1 C перпендикулярна скрещивающимися прямыми B 1 D (по обобщенной теореме о D 1 C. Найдем его. Для этого трех перпендикулярах). Из заметим, что прямоугольные соотношений D 1 C треугольники OKD и B 1 DC 1 перпендикулярна DC 1 и D 11 C подобны и OK: B 1 C 1= OD: B D. перпендикулярна B 1 D следует Отсюда OK= (по признаку перпендикулярности прямой и плоскости), что D 1 C перпендикулярна плоскости DB 1 C 1.

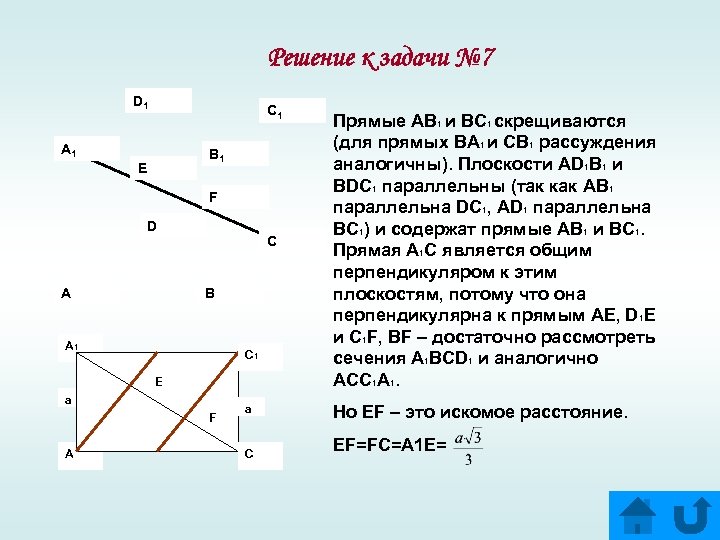Решение к задачи № 7 D 1 C 1 A 1 B 1 Е F D A C B A 1 C 1 E a F A a C Прямые AB 1 и BC 1 скрещиваются (для прямых BA 1 и CB 1 рассуждения аналогичны). Плоскости AD 1 B 1 и BDC 1 параллельны (так как AB 1 параллельна DC 1, AD 1 параллельна BC 1) и содержат прямые AB 1 и BC 1. Прямая A 1 C является общим перпендикуляром к этим плоскостям, потому что она перпендикулярна к прямым AE, D 1 E и C 1 F, BF – достаточно рассмотреть сечения A 1 BCD 1 и аналогично ACC 1 A 1. Но EF – это искомое расстояние. EF=FC=A 1 E=

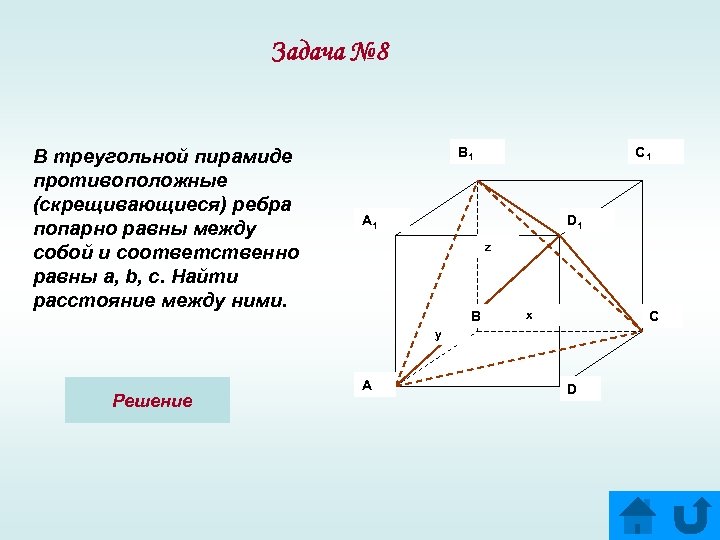Задача № 8 В треугольной пирамиде противоположные (скрещивающиеся) ребра попарно равны между собой и соответственно равны а, b, c. Найти расстояние между ними. B 1 C 1 A 1 D 1 z B x C y Решение A D

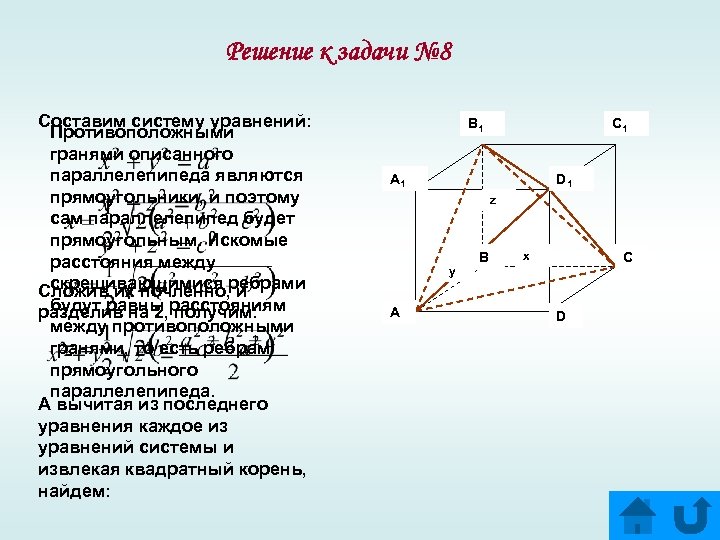Решение к задачи № 8 Составим систему уравнений: Противоположными гранями описанного параллелепипеда являются прямоугольники, и поэтому сам параллелепипед будет прямоугольным. Искомые расстояния между скрещивающимися ребрами Сложив их почленно, и будут равны расстояниям разделив на 2, получим: между противоположными гранями, то есть ребрам прямоугольного параллелепипеда. А вычитая из последнего уравнения каждое из уравнений системы и извлекая квадратный корень, найдем: B 1 C 1 A 1 D 1 z y A B x C D

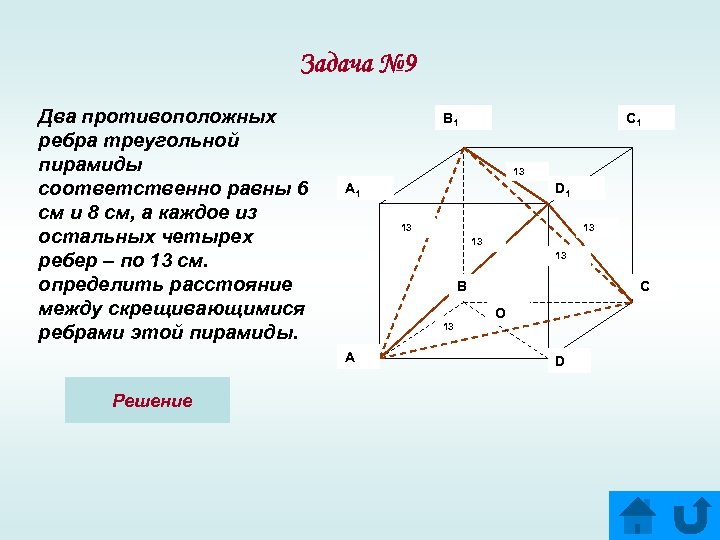Задача № 9 Два противоположных ребра треугольной пирамиды соответственно равны 6 см и 8 см, а каждое из остальных четырех ребер – по 13 см. определить расстояние между скрещивающимися ребрами этой пирамиды. B 1 13 A 1 D 1 13 13 B 13 A Решение C 1 C O D

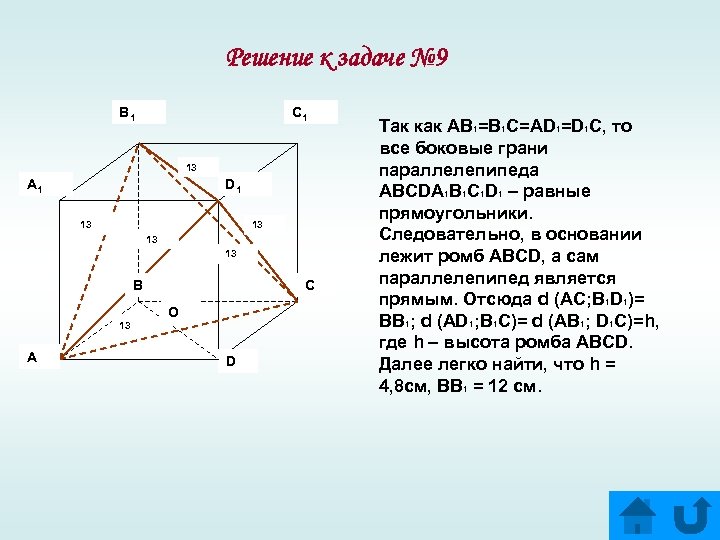Решение к задаче № 9 B 1 C 1 13 A 1 D 1 13 13 B 13 A C O D Так как AB 1=B 1 C=AD 1=D 1 C, то все боковые грани параллелепипеда ABCDA 1 B 1 C 1 D 1 – равные прямоугольники. Следовательно, в основании лежит ромб ABCD, а сам параллелепипед является прямым. Отсюда d (AC; B 1 D 1)= BB 1; d (AD 1; B 1 C)= d (AB 1; D 1 C)=h, где h – высота ромба ABCD. Далее легко найти, что h = 4, 8 см, BB 1 = 12 см.

Задача № 10 Каждое ребро треугольной призмы равно а. Одно из боковых ребер образует с прилежащими сторонами основания углы, каждый из которых равен α. Определить расстояние между этим ребром и скрещивающейся с ним стороной основания.

Решение к задачи № 10 Опустим из точки D перпендикуляр Требуется определить расстояние DК на АА 1: DК ВС. Известно. Что если между АА 1 и – искомое расстояние между ВС и АА 1. Пусть уголвершины наклонная, исходящая из А 1 АО=х; применив теорему 1 к трехгранному угла, образует со сторонами этого углу АА 1 DС, получим : проекция угла равные углы. То наклонной на плоскость угла будет его биссектрисой. Поэтому АО – биссектриса угла ВАС. Но треугольник АВС – правильный, Осталось найти КD из продолжение АКD: треугольника АD биссектрисы будет высотой этого треугольника и поэтому АD перпендикулярна ВС. По обобщенной теореме о трех перпендикулярах ВС перпендикулярна АА 1, а на основании обобщенного признака перпендикулярности прямой и плоскости ВС перпендикулярна пл. DAA 1.

Задача № 11 Определить расстояние между скрещивающимися высотами граней правильного тетраэдра с ребром а.

Решение к задачи № 11 Из. Определим расстояние между BD и подобия треугольников SOK и OPK: Аналогично находится расстояние SM. Для этого через точку M между BD и CN. Плоскость NCH проведем МЕ параллельную BD. параллельна BD. Строим Плоскость SME и BD параллельны. плоскость NO 1 L, Найдем расстояние от точки O, перпендикулярную NCH. Тогда принадлежащей BD, кдо плоскости искомым этого проведем ОК SME. Для расстоянием будет длина отрезка перпендикуляра O 1 F, перпендикулярную МЕ и соединим опущенного МE перпендикулярна точки S и К; из точки О 1 на плоскость МЕ перпендикулярна SK, откуда NCH. Из подобия треугольников NO следует, пл. SOK , а из этого 1 L и NO 1 F что находим: пл. SOK перпендикулярна пл. SME. Перпендикуляр ОР, опущенный из точки О на плоскость SME, лежит в плоскости SOK, а основание его – точка Р- лежит на прямой SK, являющейся линией пересечения этих двух взаимно перпендикулярных плоскостей.

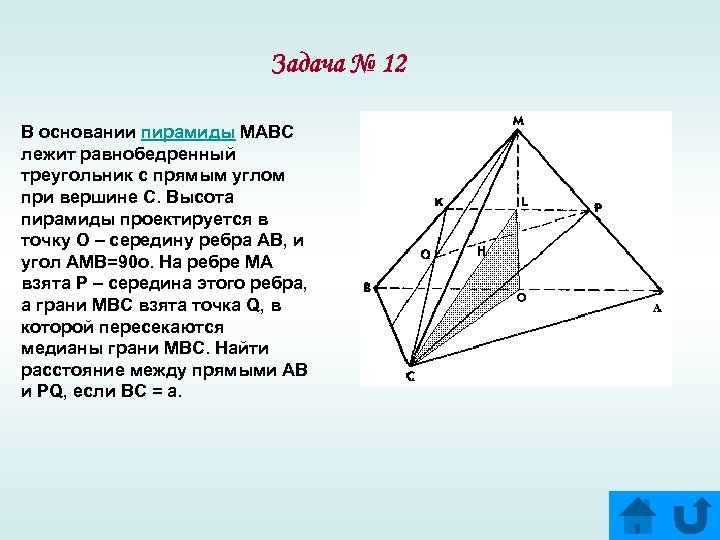Задача № 12 В основании пирамиды МАВС лежит равнобедренный треугольник с прямым углом при вершине С. Высота пирамиды проектируется в точку О – середину ребра АВ, и угол АМВ=90 o. На ребре МА взята P – середина этого ребра, а грани МВС взята точка Q, в которой пересекаются медианы грани МВС. Найти расстояние между прямыми АВ и PQ, если ВС = а.

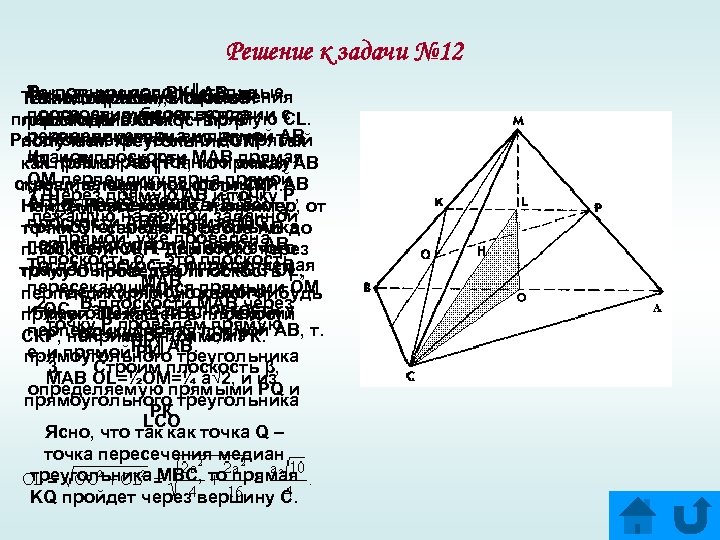Решение к задачи № 12 Выполним дополнительные Так как прямая РК║АВ, то Находим линию пересечения Таким образом, искомое Таким образом, в сечении построения в соответствии с плоскость γ будет тогда плоскостей СКР и γ – прямую CL. расстояние ОН. пирамиды плоскостью β рекомендуемым выше перпендикулярна и прямой АВ. Расстояние от точки О до прямой получаем треугольник СКР. Так планом. Итак, в плоскости МАВ прямая СL равно расстоянию между как прямая АВ║РК, то прямая АВ ОМ перпендикулярна прямой скрещивающимися прямыми АВ параллельна плоскости СКР. 1. Через прямую АВ и точку P, АВ, и, легко убедиться, в и PQ. Найдем его как высоту Найдем расстояние, например, от лежащую на другой заданной плоскости АВС прямая ОС прямоугольного треугольника точки О –середины ребра АВ до прямой, уже проведена перпендикулярна прямой АВ. LCO. Если ОН – высота этого плоскости СКР. Для этого через плоскость α – это плоскость Тогда плоскость, определяемая треугольника, то ОН∙СL=OC∙OL, точку О проведем плоскость γ , МАВ. пересекающимися прямыми ОМ где из прямоугольного перпендикулярную какой-нибудь 2. В плоскости МАВ через и ОС, - это и есть плоскость γ треугольника АВС находим прямой. Лежащей в плоскости точку Р проведем прямую перпендикулярная прямой АВ, т. ОС=½АВ=½ а√ 2, из СКР, например, прямой РК. РК║АВ. е. и прямой РК. прямоугольного треугольника 3. Строим плоскость β, МАВ OL=½OM=¼ a√ 2, и из определяемую прямыми PQ и прямоугольного треугольника РК. LCO Ясно, что так как точка Q – точка пересечения медиан треугольника МВС, то прямая KQ пройдет через вершину С.

Справочник. 1 теорема 2 прямая 3 отрезок 4 прямоугольник 5 ромб 6 квадрат 7 высота в треугольнике 8 медиана в треугольнике 9 биссектриса в треугольнике 10 наклонная 11 многогранник 12 призма 13 параллелепипед 14 доказательство 15 признак перпендикулярности прямой и плоскости 16 теорема о трех перпендикулярах