Лекция 1 (вероятность случайных событий).pptx
- Количество слайдов: 22

ТЕОРИЯ ВЕРОЯТНОСТИ Лекция 1 Вероятность случайных событий доцент: Колосько Анатолий Григорьевич ( agkolosko@mail. ru )

Детерминизм и случайность Детермини зм ‒ учение о взаимосвязи происходящих процессов и явлений нашего мира, доктрина всеобщей причинности (если наоборот - это индетерминизм). - теологический детерминизм : все события в мире определены Богом; - космологический детерминизм : всё определяется явлениями природы; - антропологическо-этический детерминизм : всё решает человеческая воля, но для её свободы не остаётся места; - фатализм : крайний случай детерминизма, вера в предопределённость бытия. В окружающей нас реальности действуют два основных типа законов: законы жёсткой детерминации и статистические законы. Законы обоих типов объективны и несводимы друг к другу. Детерминистические законы – это низший уровень процесса познания мира. Статистические законы отражают объективные связи в природе и являются более высоким этапом познания, учитывающим СЛУЧАЙНОСТЬ процессов. Теория вероятностей – раздел математики, изучающий вероятности событий, в нём разрабатываются методы, с помощью которых можно вычислить вероятности одних событий, зная вероятности других. Является основой статистических расчётов.

Три основных понятия Случайный эксперимент – эксперимент, который может закончиться любым из некоторого множества известных результатов, но каким именно заранее не известно. Исход – результат случайного эксперимента. Множество Ω : Пространство элементарных исходов – множество всех взаимно исключающих (не могут наступить одновременно) исходов эксперимента. Обозначается буквой Ω. Случайное событие – это определённое множество исходов (подмножество множества Ω). Обозначается большими буквами: А, В, С. . . Говорят, что событие А наступило, если эксперимент закончился одним из исходов, входящих в это событие. р. фунт $ € ₤ гривна иена ₴ ¥ Эксперимент: тащим из коробки 1 купюру событие А : $ € ₤
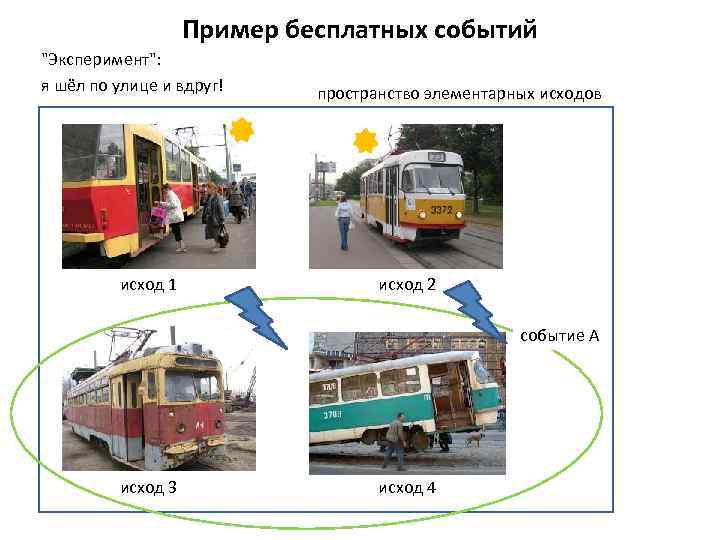
Пример бесплатных событий "Эксперимент": я шёл по улице и вдруг! исход 1 пространство элементарных исходов исход 2 событие А исход 3 исход 4
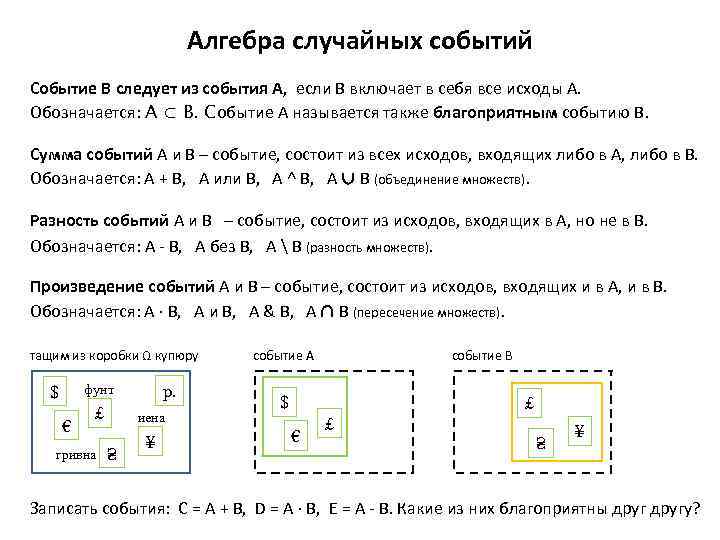
Алгебра случайных событий Событие В следует из события А, если В включает в себя все исходы А. Обозначается: А ⊂ В. Событие А называется также благоприятным событию В. Сумма событий А и В – событие, состоит из всех исходов, входящих либо в А, либо в В. Обозначается: А + В, А или В, А ˄ В, А ∪ В (объединение множеств). Разность событий А и В – событие, состоит из исходов, входящих в А, но не в В. Обозначается: А - В, А без В, А В (разность множеств). Произведение событий А и В – событие, состоит из исходов, входящих и в А, и в В. Обозначается: А · В, А и В, А & В, А ∩ В (пересечение множеств). тащим из коробки Ω купюру р. фунт $ € ₤ гривна иена ₴ ¥ событие А событие В $ ₤ € ₤ ₴ ¥ Записать события: С = А + В, D = A · B, E = A - B. Какие из них благоприятны другу?
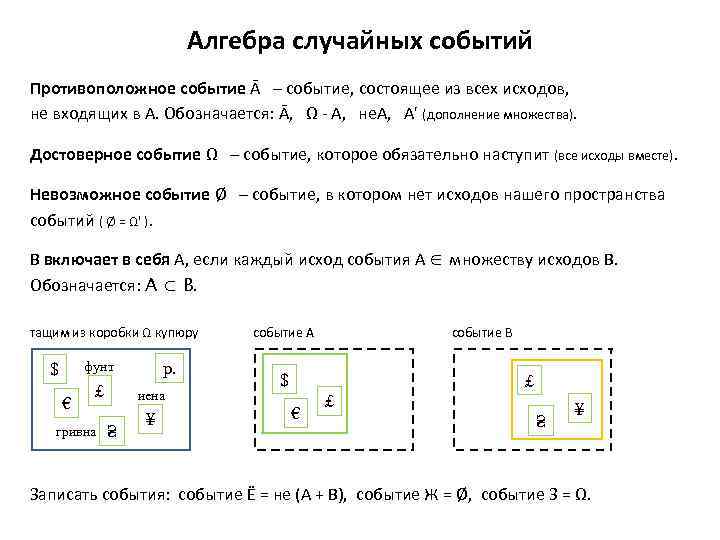
Алгебра случайных событий Противоположное событие Ā – событие, состоящее из всех исходов, не входящих в А. Обозначается: Ā, Ω - А, не. А, A' (дополнение множества). Достоверное событие Ω – событие, которое обязательно наступит (все исходы вместе). Невозможное событие Ø – событие, в котором нет исходов нашего пространства событий ( Ø = Ω' ). В включает в себя А, если каждый исход события А ∈ множеству исходов В. Обозначается: А ⊂ В. тащим из коробки Ω купюру р. фунт $ € ₤ гривна иена ₴ ¥ событие А событие В $ ₤ € ₤ ₴ ¥ Записать события: событие Ё = не (А + В), событие Ж = Ø, событие З = Ω.

Задача с бесплатным экспериментом событие А - ударила молния "Эксперимент" событие В - сел в трамвай Перечислить исходы событий: исход 1 исход 2 событие С = А + В событие D = A · B событие E = A - B событие Ё = не (А + В) событие Ж = Ø исход 3 исход 4 событие З = Ω

Изображение событий перечислением Стандартное изображение событий - перечисление их элементов: А = {а 1, а 2, а 3, . . . }. Записать события: А+В, А-В, В-А.
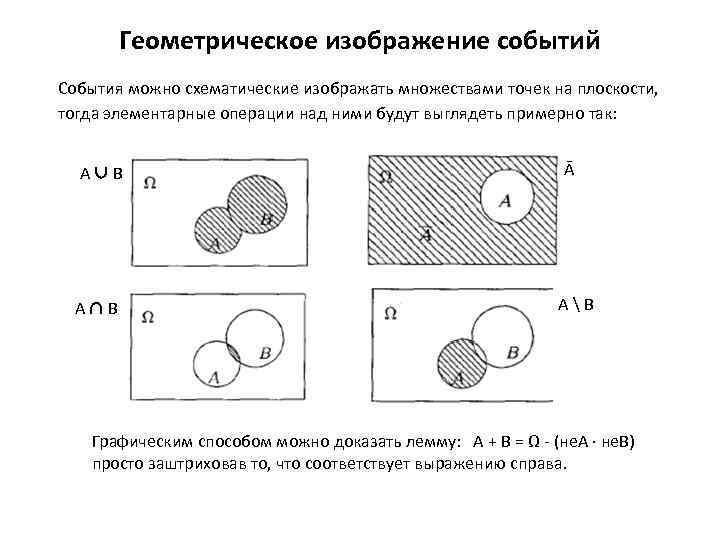
Геометрическое изображение событий События можно схематические изображать множествами точек на плоскости, тогда элементарные операции над ними будут выглядеть примерно так: А ∪ В А ∩ В Ā А В Графическим способом можно доказать лемму: А + В = Ω - (не. А · не. В) просто заштриховав то, что соответствует выражению справа.
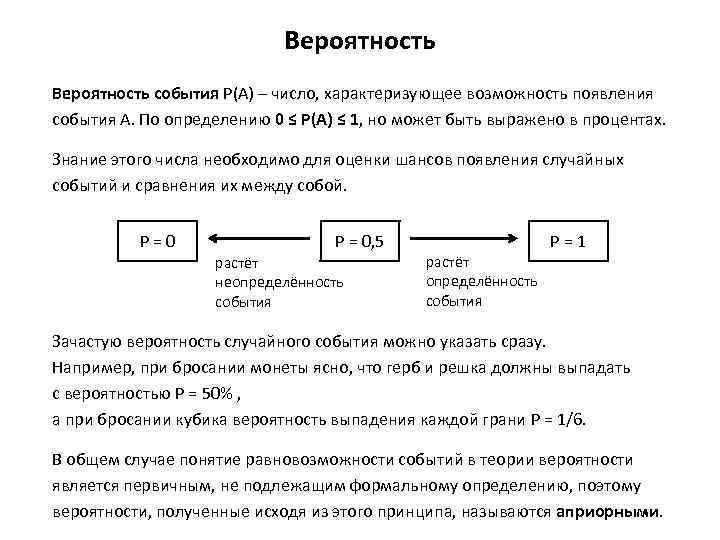
Вероятность события Р(А) – число, характеризующее возможность появления события А. По определению 0 ≤ Р(А) ≤ 1, но может быть выражено в процентах. Знание этого числа необходимо для оценки шансов появления случайных событий и сравнения их между собой. P = 0, 5 растёт неопределённость события растёт определённость события P = 1 Зачастую вероятность случайного события можно указать сразу. Например, при бросании монеты ясно, что герб и решка должны выпадать с вероятностью P = 50% , а при бросании кубика вероятность выпадения каждой грани P = 1/6. В общем случае понятие равновозможности событий в теории вероятности является первичным, не подлежащим формальному определению, поэтому вероятности, полученные исходя из этого принципа, называются априорными.

Общее определение вероятности Пусть пространство элементарных исходов имеет вид: Ω = {ω1 , . . . , ωn}, где n ≤ ∞. Поставим в соответствие каждому исходу ωi неотрицательное число P(ωi), которое будет характеризовать степень вероятности появления этого исхода, да так, чтобы выполнялось условие нормировки: Это взаимооднозначное соответствие {ω1 , . . . , ωn} ↔ { P(ω1), . . . , P(ωn) } называется распределением вероятности на Ω. (Как бы распределяем общую единицу по независимым исходам). Вероятностью события А, состоящего из исходов {ωj 1 , . . . , ωjn} - подмножество Ω, называется число P(A) равное сумме вероятностей исходов, входящих в А:

Основные свойства вероятностей 1. Базовые свойства, остальные свойства из них выводятся 2. 3. 4. Если то 5. 6. Если А и В несовместны, то 7. Для любого набора событий {А, В, . . . } , будет верной формула: Следует из леммы А + В = Ω - (не. А · не. В) Т. е. вероятность того, что произошло хотя бы одно событие из группы, можно найти, вычитая из 1 вероятность того, что не произошло ни одного события.

Пример на априорно бесплатные вероятности "Эксперимент" Считая исходы равновероятными, определите вероятности: событие А: ударила молния событие В: сел в трамвай исход 1 исход 2 событие С = А или В событие D = A и B событие E = A без B событие Ё = не (А или В) исход 3 исход 4 событие Ж = Ø событие Зе = Ω

Если исходы равновероятны. Классика Пусть все N исходов в пространстве Ω равновероятны, значит P(ωi) = po С другой стороны в силу условия нормировки ∑ P(ωi) = 1 Отсюда получаем, что ∑ po = 1 или po*N = 1, откуда po = 1 / N Найдём вероятность события А, состоящего из М исходов этого пространства Ω. По формуле классической вероятности: Р(А) = ∑ P(ωi ϵ А) а так как их М штук и все они равновероятны, то Р(А) = M * po подставляем po = 1 / N и определяем Р(А): Р(А) = M * po = M * 1 / N = M / N Таким образом, в случае равновероятных исходов можно пользоваться более простой "классической" формулой: где M - число исходов, входящих в событие А, N - число всех исходов.

Пример Из колоды карт наудачу выбирают одну карту. Найти вероятность того, что эта карта пиковой масти. Решение: всего исходов 36, у каждого вероятность = 1/36 событие А - пиковая карта содержит в себе 9 исходов (9 пиковых карт), стало быть вероятность этого события: Р(А) = 9 / 36 = 1 / 4 = 0, 25
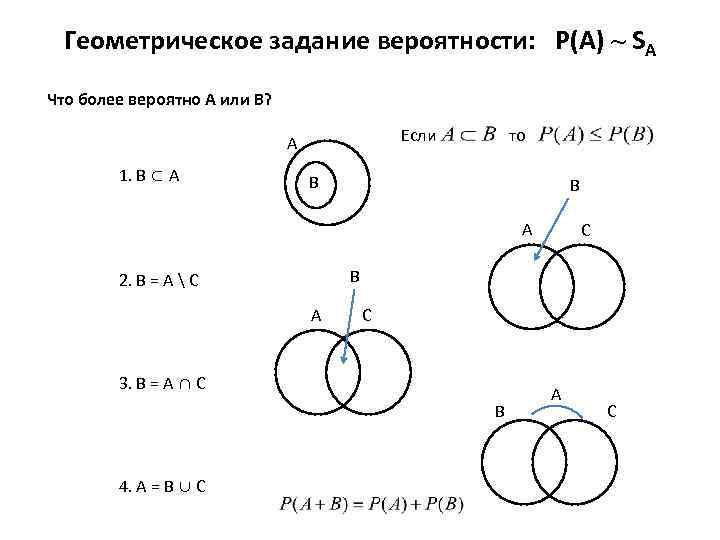
Геометрическое задание вероятности: P(А) ~ SA Что более вероятно А или В? 1. В ⊂ А Если то A B B A B 2. B = А C A C 3. В = А ∩ С B 4. А = В ∪ C C A C

Виды определения вероятности Классическое определение: отношение числа равновероятных исходов, входящих в событие А, к числу всех возможных равновероятных исходов. Геометрическое определение : отношение меры события А (например, площади мишени) к мере всего пространства исходов (к площади обстрела). Статистическое определение вероятности (концепция Мизеса): предел отношения числа появлений события А (m) в серии одинаковых испытаний (схема Бернулли) к их общему числу (n) при n стремящемся к бесконечности. Отношение числа появлений события А к числу всех проведённых экспериментов называется частотой события (ω).
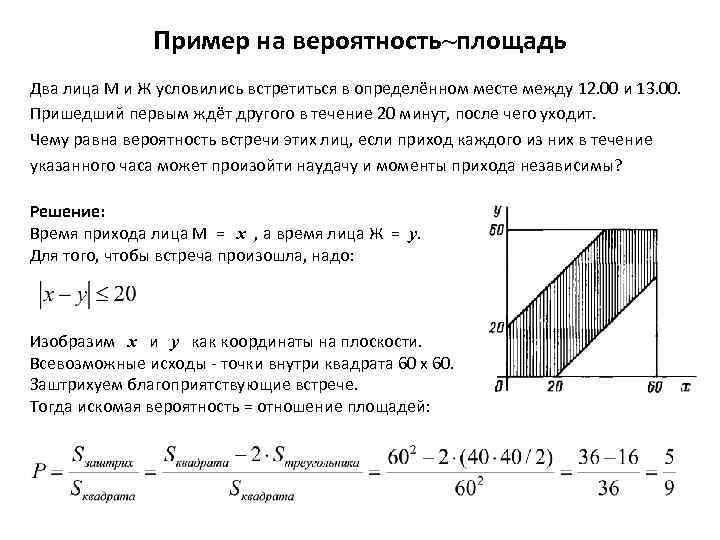
Пример на вероятность~площадь Два лица М и Ж условились встретиться в определённом месте между 12. 00 и 13. 00. Пришедший первым ждёт другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если приход каждого из них в течение указанного часа может произойти наудачу и моменты прихода независимы? Решение: Время прихода лица М = х , а время лица Ж = y. Для того, чтобы встреча произошла, надо: Изобразим х и y как координаты на плоскости. Всевозможные исходы - точки внутри квадрата 60 х 60. Заштрихуем благоприятствующие встрече. Тогда искомая вероятность = отношение площадей:

* Примеры статистической вероятности Устойчивость статистической частоты событий была обнаружена и многократно подтверждена экспериментально естествоиспытателями в 17 -19 веках.
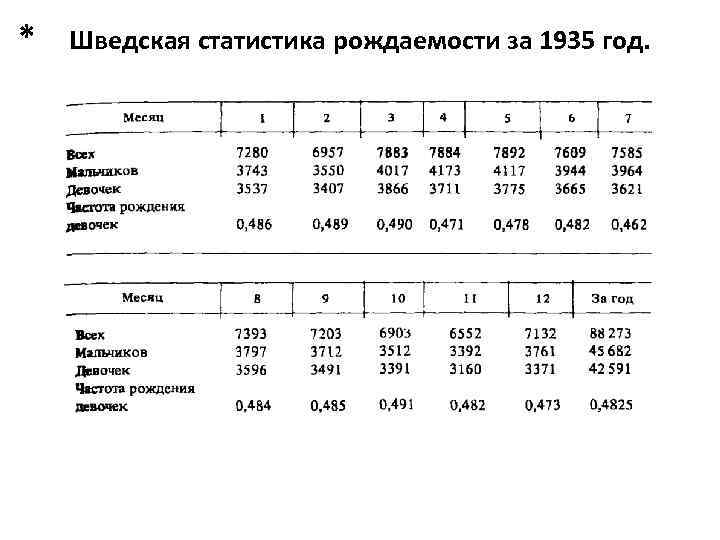
* Шведская статистика рождаемости за 1935 год.

Спасибо за внимание : )

Вопросы для контроля усвояемости предмета • • • • • Случайный эксперимент; Пространство элементарных исходов Случайное событие; Благоприятные события Сумма событий А и В; Разность событий А и В, обозначения Произведение событий А и В, обозначения Событие противоположное к событию А, обозначения Достоверное событие; Невозможное событие Геометрическое изображение событий Вероятность события; Априорная вероятность Общее определение вероятности события Свойства вероятностей событий Что более вероятно А или В, если В ⊂ А ? Что более вероятно А или В, если B = А C ? Что более вероятно А или В, если В = А ∩ С ? Что более вероятно А или В, если А = В ∪ C ? Классическое определение вероятности Геометрическое определение вероятности Частота события; Статистическое определение вероятности
Лекция 1 (вероятность случайных событий).pptx