ТВ Семенычев.ppt
- Количество слайдов: 65
 Теория вероятности и математическая статистика Лекции д. э. н. , д. т. н. , проф. В. К. Семёнычева г. Самара
Теория вероятности и математическая статистика Лекции д. э. н. , д. т. н. , проф. В. К. Семёнычева г. Самара
 Теория вероятности Лекция 1. Основные понятия теории вероятностей. Алгебра событий. Формулы вычисления вероятности.
Теория вероятности Лекция 1. Основные понятия теории вероятностей. Алгебра событий. Формулы вычисления вероятности.
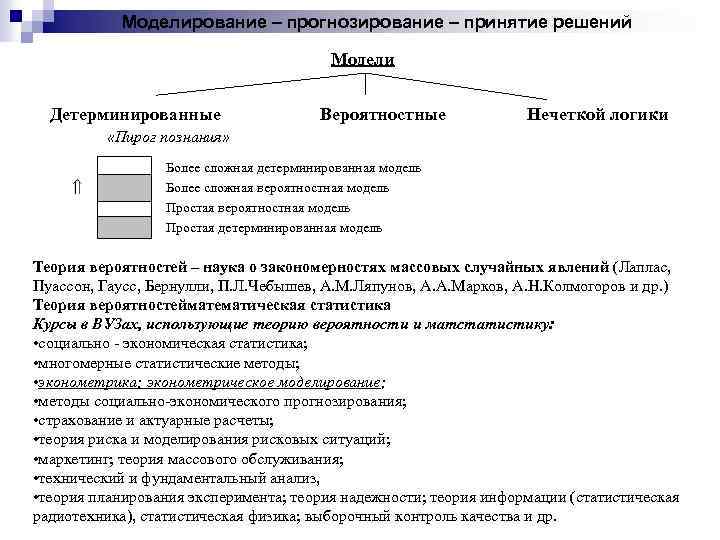 Моделирование – прогнозирование – принятие решений Модели Детерминированные Вероятностные Нечеткой логики «Пирог познания» Более сложная детерминированная модель Более сложная вероятностная модель Простая детерминированная модель Теория вероятностей – наука о закономерностях массовых случайных явлений (Лаплас, Пуассон, Гаусс, Бернулли, П. Л. Чебышев, А. М. Ляпунов, А. А. Марков, А. Н. Колмогоров и др. ) Теория вероятностейматематическая статистика Курсы в ВУЗах, использующие теорию вероятности и матстатистику: • социально - экономическая статистика; • многомерные статистические методы; • эконометрика; эконометрическое моделирование; • методы социально-экономического прогнозирования; • страхование и актуарные расчеты; • теория риска и моделирования рисковых ситуаций; • маркетинг; теория массового обслуживания; • технический и фундаментальный анализ, • теория планирования эксперимента; теория надежности; теория информации (статистическая радиотехника), статистическая физика; выборочный контроль качества и др.
Моделирование – прогнозирование – принятие решений Модели Детерминированные Вероятностные Нечеткой логики «Пирог познания» Более сложная детерминированная модель Более сложная вероятностная модель Простая детерминированная модель Теория вероятностей – наука о закономерностях массовых случайных явлений (Лаплас, Пуассон, Гаусс, Бернулли, П. Л. Чебышев, А. М. Ляпунов, А. А. Марков, А. Н. Колмогоров и др. ) Теория вероятностейматематическая статистика Курсы в ВУЗах, использующие теорию вероятности и матстатистику: • социально - экономическая статистика; • многомерные статистические методы; • эконометрика; эконометрическое моделирование; • методы социально-экономического прогнозирования; • страхование и актуарные расчеты; • теория риска и моделирования рисковых ситуаций; • маркетинг; теория массового обслуживания; • технический и фундаментальный анализ, • теория планирования эксперимента; теория надежности; теория информации (статистическая радиотехника), статистическая физика; выборочный контроль качества и др.
 Моделирование – прогнозирование – принятие решений Предмет теории вероятностей – явления, события, случайные величины (одномерные, многомерные) Наблюдаемые явления (результат испытаний) Достоверные Условия: t=+20 C, P- норм. Вода в сосуде – жидкая Невозможные Условия t=+20 C, Р – норм Вода в сосуде – твердая Случайные Испытание бросание монеты (герб или цифра) События A, B, C, … - несовместные, если появление одного из них исключает появление других событий в одном и том же испытании. События образуют полную группу событий, если в результате испытаний появится хотя бы одно из них.
Моделирование – прогнозирование – принятие решений Предмет теории вероятностей – явления, события, случайные величины (одномерные, многомерные) Наблюдаемые явления (результат испытаний) Достоверные Условия: t=+20 C, P- норм. Вода в сосуде – жидкая Невозможные Условия t=+20 C, Р – норм Вода в сосуде – твердая Случайные Испытание бросание монеты (герб или цифра) События A, B, C, … - несовместные, если появление одного из них исключает появление других событий в одном и том же испытании. События образуют полную группу событий, если в результате испытаний появится хотя бы одно из них.
 Моделирование – прогнозирование – принятие решений Вероятность – мера объективной возможности появления события. Классическое определение вероятности: , где m – число исходов испытания, которое благоприятствует появлению события A, n – общее число исходов испытания.
Моделирование – прогнозирование – принятие решений Вероятность – мера объективной возможности появления события. Классическое определение вероятности: , где m – число исходов испытания, которое благоприятствует появлению события A, n – общее число исходов испытания.
 Моделирование – прогнозирование – принятие решений
Моделирование – прогнозирование – принятие решений

 Алгебра событий
Алгебра событий
 Алгебра событий
Алгебра событий
 Алгебра событий
Алгебра событий
 Алгебра событий
Алгебра событий
 Доказательство теоремы о сложении вероятностей совместных событий
Доказательство теоремы о сложении вероятностей совместных событий
 Формула полной вероятности
Формула полной вероятности
 Формула вероятности гипотез
Формула вероятности гипотез
 Формула вероятности гипотез
Формула вероятности гипотез
 Формула Бернулли
Формула Бернулли
 Локальная формула Лапласа
Локальная формула Лапласа
 Интегральная формула Лапласа
Интегральная формула Лапласа
 Лекция 2 Понятие случайной величины. Числовые характеристики. Законы распределения непрерывных и дискретных случайных величин.
Лекция 2 Понятие случайной величины. Числовые характеристики. Законы распределения непрерывных и дискретных случайных величин.
 Случайные одномерные величины
Случайные одномерные величины
 Случайные одномерные величины
Случайные одномерные величины
 Случайные одномерные величины
Случайные одномерные величины
 Случайные одномерные величины
Случайные одномерные величины
 Основные формулы комбинаторики, используемые для определения вероятностей алгебры событий
Основные формулы комбинаторики, используемые для определения вероятностей алгебры событий
 Функция (интегральный закон) распределения с. в.
Функция (интегральный закон) распределения с. в.
 Плотность вероятности (дифференциальный закон) распределения непрерывной с. в.
Плотность вероятности (дифференциальный закон) распределения непрерывной с. в.
 Числовые характеристики распределения с. в.
Числовые характеристики распределения с. в.
 Числовые характеристики распределения с. в.
Числовые характеристики распределения с. в.
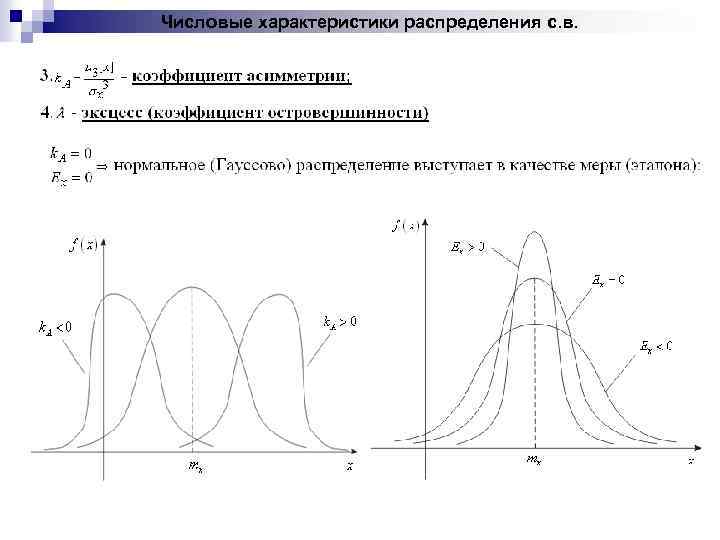 Числовые характеристики распределения с. в.
Числовые характеристики распределения с. в.
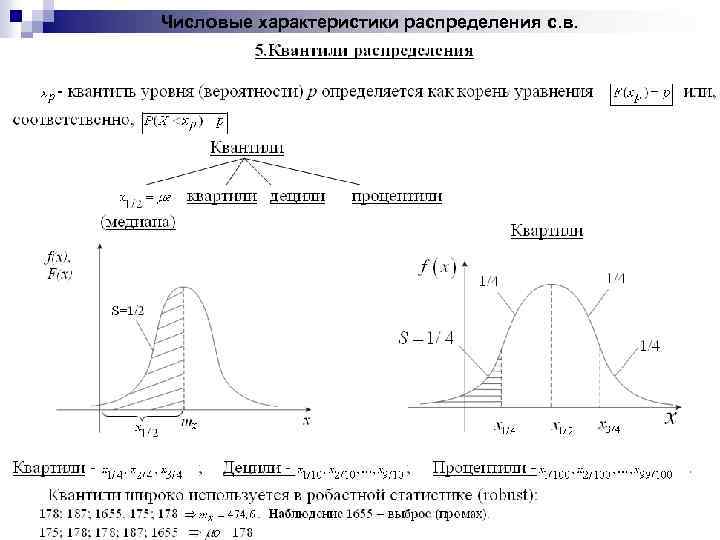 Числовые характеристики распределения с. в.
Числовые характеристики распределения с. в.
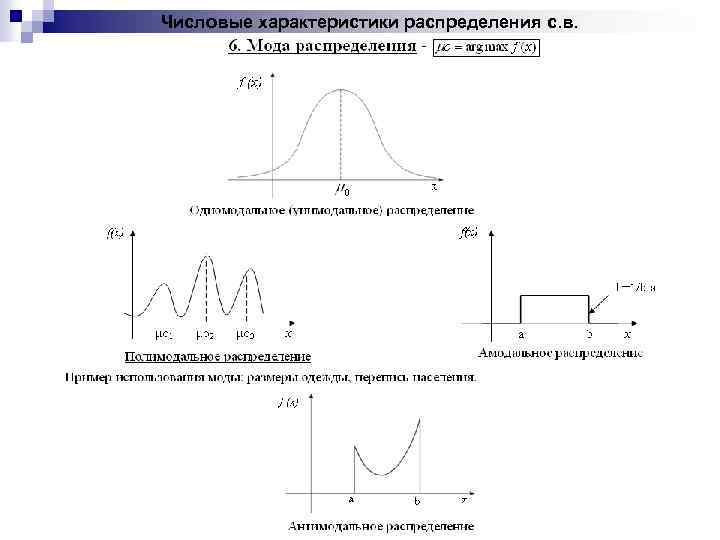 Числовые характеристики распределения с. в.
Числовые характеристики распределения с. в.
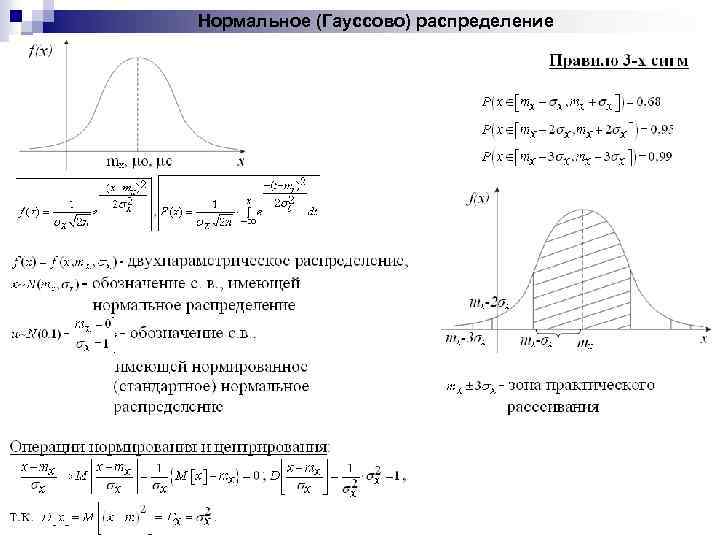 Нормальное (Гауссово) распределение
Нормальное (Гауссово) распределение
 Функция Лапласа
Функция Лапласа
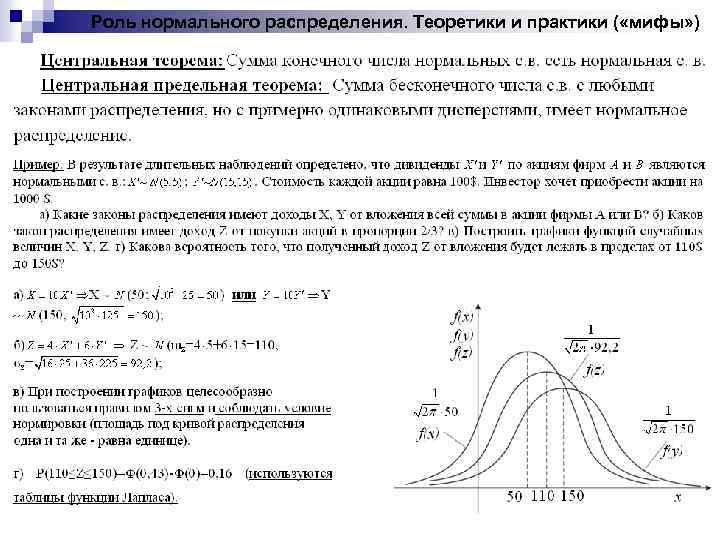 Роль нормального распределения. Теоретики и практики ( «мифы» )
Роль нормального распределения. Теоретики и практики ( «мифы» )
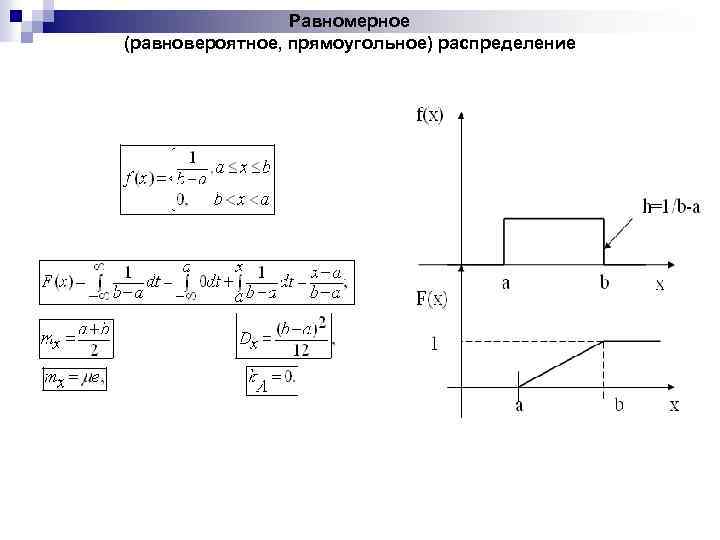 Равномерное (равновероятное, прямоугольное) распределение
Равномерное (равновероятное, прямоугольное) распределение
 Показательное (экспоненциальное) распределение
Показательное (экспоненциальное) распределение
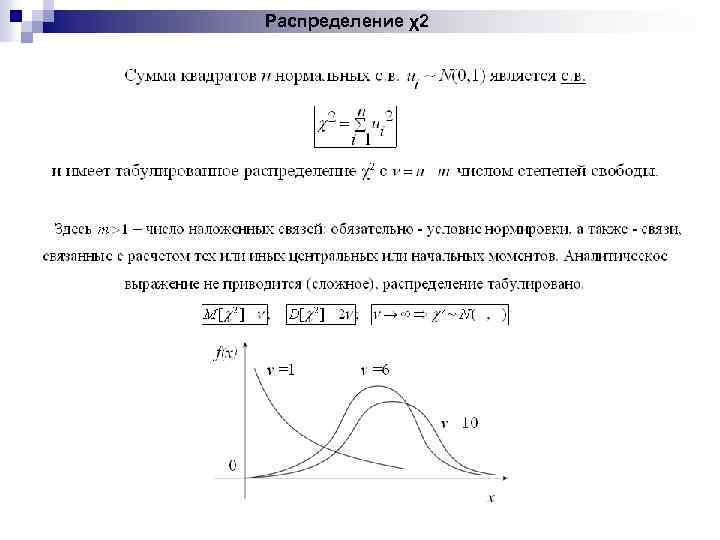 Распределение χ2
Распределение χ2
 Т - распределение (Стьюдента- лорда Госсета)
Т - распределение (Стьюдента- лорда Госсета)
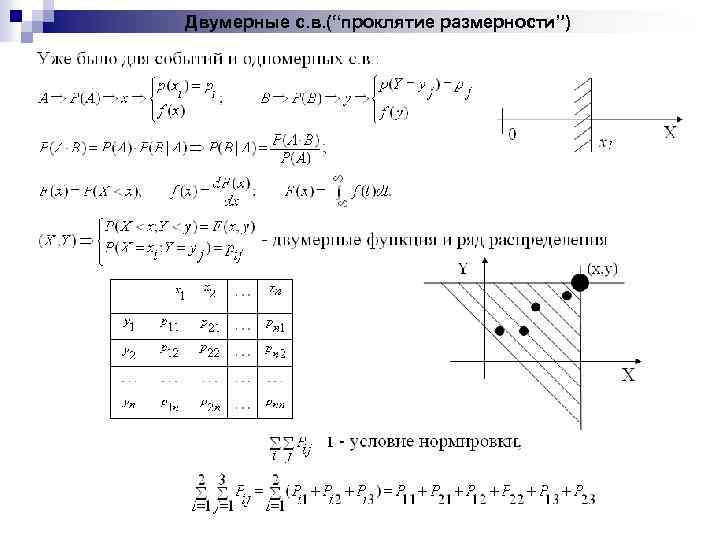 Двумерные с. в. (“проклятие размерности”)
Двумерные с. в. (“проклятие размерности”)
 Двумерные с. в.
Двумерные с. в.
 Двумерные с. в.
Двумерные с. в.
 Условные математические ожидания (регрессии)
Условные математические ожидания (регрессии)
 ЛЕКЦИЯ 3. Основные понятия математической статистики. Функциональная, статистическая и корреляционная зависимости. Проверка истинности статистических гипотез. Коэффициент корреляции. Регрессия. Виды регрессии.
ЛЕКЦИЯ 3. Основные понятия математической статистики. Функциональная, статистическая и корреляционная зависимости. Проверка истинности статистических гипотез. Коэффициент корреляции. Регрессия. Виды регрессии.
 Задачи математической статистики
Задачи математической статистики
 Свойства эмпирической функции распределения:
Свойства эмпирической функции распределения:
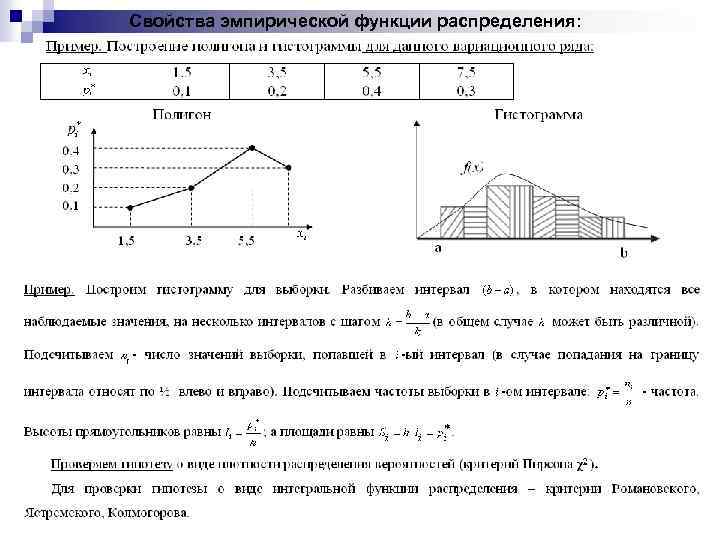 Свойства эмпирической функции распределения:
Свойства эмпирической функции распределения:
 Статистические оценки параметров распределения
Статистические оценки параметров распределения
 Точечные оценки точности оценок (статистик) генеральных числовых характеристик
Точечные оценки точности оценок (статистик) генеральных числовых характеристик
 Точечные оценки точности оценок (статистик) генеральных числовых характеристик
Точечные оценки точности оценок (статистик) генеральных числовых характеристик
 Интервальная оценка точности (надежность) генеральных математического ожидания и дисперсии
Интервальная оценка точности (надежность) генеральных математического ожидания и дисперсии
 Интервальная оценка точности (надежность) генеральных математического ожидания и дисперсии
Интервальная оценка точности (надежность) генеральных математического ожидания и дисперсии
 Доверительные интервалы оценки среднеквадратического отклонения Методы оценки параметров известного распределения
Доверительные интервалы оценки среднеквадратического отклонения Методы оценки параметров известного распределения
 Методы оценки параметров известного распределения
Методы оценки параметров известного распределения
 Методы оценки параметров известного распределения
Методы оценки параметров известного распределения
 Методы оценки параметров известного распределения
Методы оценки параметров известного распределения
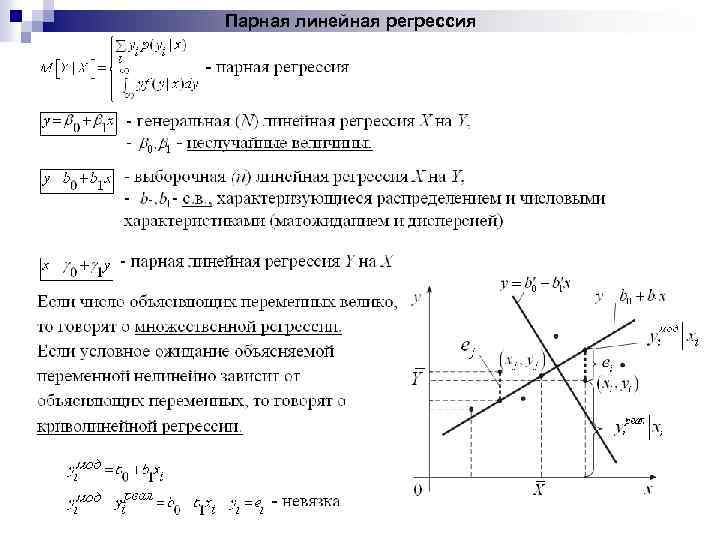 Парная линейная регрессия
Парная линейная регрессия
 Парная линейная регрессия
Парная линейная регрессия
 Парная линейная регрессия
Парная линейная регрессия
 Множественная линейная регрессия
Множественная линейная регрессия
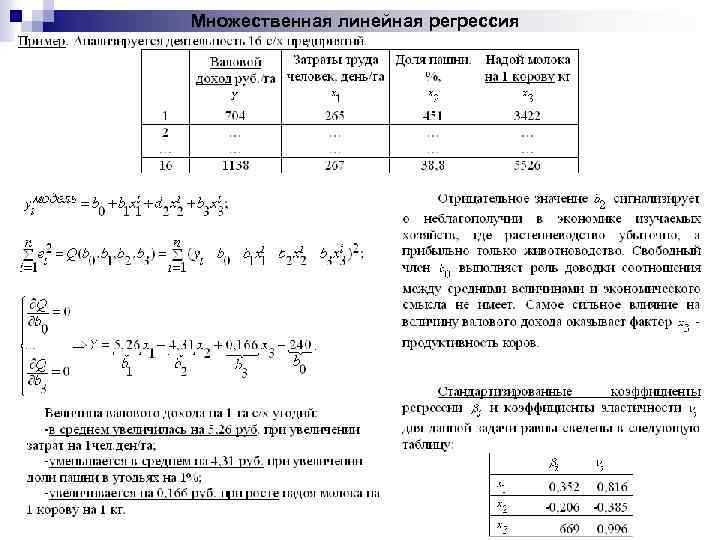 Множественная линейная регрессия
Множественная линейная регрессия
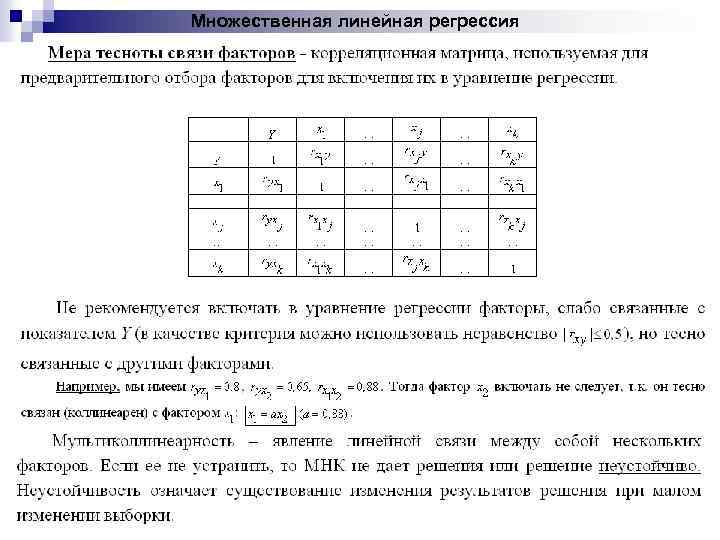 Множественная линейная регрессия
Множественная линейная регрессия
 Коэффициент детерминации регрессий
Коэффициент детерминации регрессий
 Коэффициент детерминации регрессий
Коэффициент детерминации регрессий
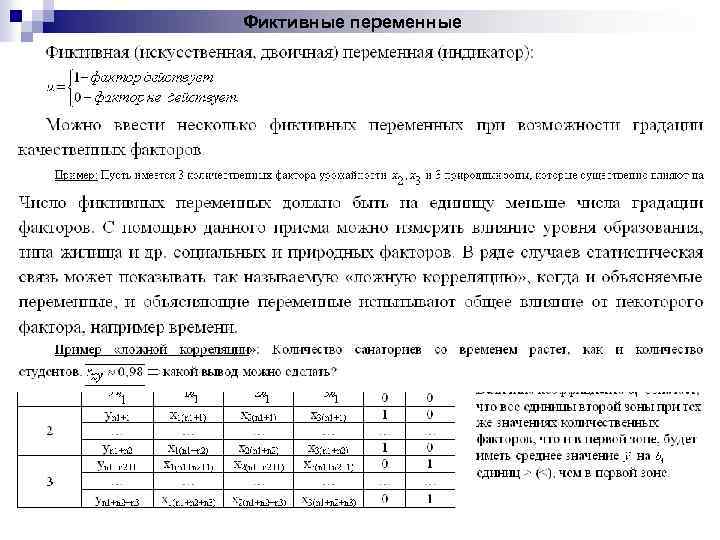 Фиктивные переменные
Фиктивные переменные
 Литература 1. Гмурман В. Е. Теория вероятностей и математическая статистика. М. Высшая школа. 2003 2. Теория статистики/ Р. А. Шмойлова и др. М. : Финансы и статистика. 2004. 3. Елисеева И. И. , Юзбашев Общая теория статистики. М. : Финансы и статистика. 2004. 4. Вентцель Е. С. Теория вероятности. (Любой год издания) Дамский мастер и др. И. Грекова.
Литература 1. Гмурман В. Е. Теория вероятностей и математическая статистика. М. Высшая школа. 2003 2. Теория статистики/ Р. А. Шмойлова и др. М. : Финансы и статистика. 2004. 3. Елисеева И. И. , Юзбашев Общая теория статистики. М. : Финансы и статистика. 2004. 4. Вентцель Е. С. Теория вероятности. (Любой год издания) Дамский мастер и др. И. Грекова.


