Теория вероятностей Теория вероятностей — это математическая наука,

Теория вероятностей Теория вероятностей — это математическая наука, изучающая вероятностные закономерности массовых однородных случайных событий.

1. Пространство элементарных событий Изучение какого-либо явления в порядке наблюдения будем называть испытанием. Всякий результат или исход испытания является событием. События обычно обозначаются заглавными латинскими буквами A, B, C и т.д. Пусть события, которые могут произойти в результате некоторого испытания, образуют систему S. 1. Событие называется достоверным, если оно является единственно возможным исходом испытания при заданной совокупности условий. Событие называется невозможным, если оно не может произойти при заданных условиях. 2. Если при каждом испытании, при котором происходит событие A, происходит также и событие B, то будем говорить, что A влечет за собой B. A  B (B  A). 3. Если событие A влечет за собой событие B и в то же время B влечет за собой A, т.е. при каждом испытании события A и B оба наступают или не наступают, то будем говорить, что события A и B равносильны. A = B. В дальнейшем будем обозначать достоверные события буквой U, а невозможные события — буквой V.

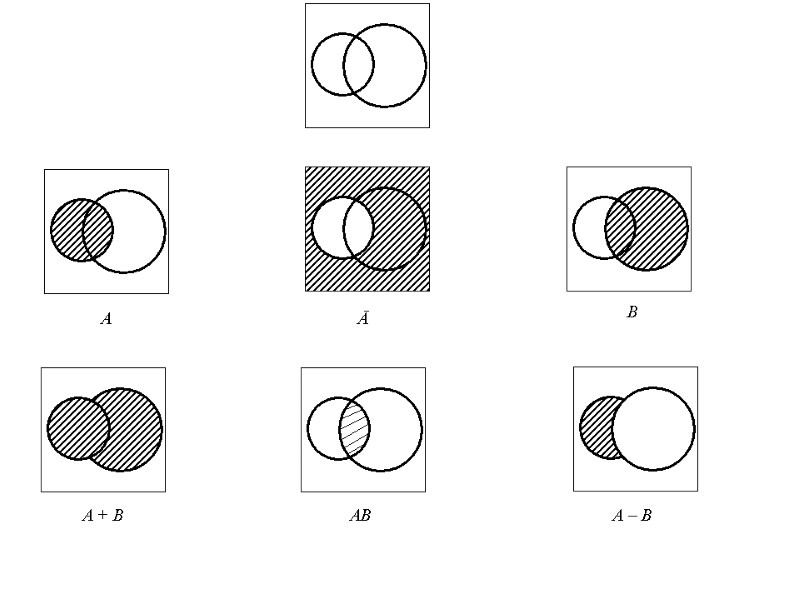
4. Событие, состоящее в наступлении обоих событий A и B, будем называть произведением событий A и B A · B (или A  B). 5. Событие, состоящее в наступлении хотя бы одного из событий A и B, будем называть суммой событий A и B A + B (или A  B). Определение суммы и произведения обобщается на любое число событий. Пусть даны события A, B, …, N. A + B + … + N означает событие, заключающееся в наступлении хотя бы одного из событий A, B, …, N. A·B · … · N означает событие, состоящее в наступлении всех событий A, B, …, N. 6. Событие, состоящее в том, что событие A происходит, а событие B не происходит, будем называть разностью событий A и B A – B. 7. События A и Ā называются противоположными, если для них одновременно выполняются два соотношения: A + Ā = U, A · Ā = V.

A Ā B A + B AB A – B

8. Два события A и B называются несовместимыми, если их совместное появление невозможно, т.е., если AB = V. Если A = B1 + B2 + … + Bn и события Bi попарно несовместимы, т.е. Bi Bj = V при i  j, то говорят, что событие A подразделяется на частные случаи B1, B2, …, Bn. События B1, B2, …, Bn образуют полную группу событий, если хотя бы одно из них при данном испытании должно произойти, т.е. если B1 + B2 + … + Bn = U. Особенно существенны для нас в дальнейшем будут полные группы попарно несовместимых событий. 9. В каждой задаче теории вероятностей приходится иметь дело с какой-либо определенной системой событий S, наступающих или нет при том или ином испытании. Относительно такой системы событий целесообразно сделать следующие допущения: а) если системе, S принадлежат события A и B, то ей принадлежат и события A + B, AB, A – B; б) система S содержит невозможное и допустимое события. Система событий, удовлетворяющая этим допущениям, называется полем событий.

Неразложимые события называются элементарными. Множество элементарных событий данного испытания составляют пространство элементарных событий. При этом природа элементов этого пространства заранее не оговаривается, поскольку важно иметь достаточно широкий выбор для охвата всех возможных случаев. Множества точек пространства элементарных событий образуют случайные события. Те элементарные исходы (события), в которых наступает интересующее событие, назовём благоприятствующими этому событию. Для случайных событий имеют место следующие законы: Коммутативный: A + B = B + A, AB = BA; Ассоциативный: A + (B + C) = (A + B) + C, A(BC) = (AB) C; Дистрибутивный: A(B + C) = AB + АC; Тождества: A + A = A, AA = A.

2. Классическое определение вероятности события В общем случае рассмотрим какую-нибудь группу G, состоящую из n попарно несовместимых равновозможных событий E1, E2, …, En. Образуем систему S, состоящую из невозможного события V, всех событий Ek группы G и всех событий A, которые могут быть подразделены на частные случаи, входящие в состав группы G. Например, если группа G состоит из трех событий E1, E2 и E3, то в систему S входят события V, E1, E2, E3, E1 + E2, E1 + E3, E2 + E3, U = E1 + E2 + E3. Такая система S образует поле событий. Если событие A подразделяется на m частных случаев, входящих в полную группу из n попарно несовместимых и равновозможных событий, то вероятность p(A) события A равна Например, при однократном бросании игральной кости полная группа попарно несовместимых и равновероятных событий состоит из событий E1, E2, …, E6, которые состоят соответственно в выпадении 1, 2, …, 6 очков. Событие C = E2 + E4 + E6, состоящее в выпадении четного числа очков, подразделяется на три частных случая, входящих в состав полной группы несовместимых и равновероятных событий. Поэтому

В соответствии с приведенным определением каждому событию A принадлежащему построенному полю событий S, приписывается вполне определенная вероятность p(A). Таким образом, вероятность p(A) можно рассматривать как функцию от события A, определенную на поле событий S. Эта функция обладает следующими свойствами. Для каждого события А поля S p(A)  0. 2. Для достоверного события U p(U) = 1. 3. Если событие А подразделяется на частные случаи В и С и все три события А, В, С принадлежат полю S, то Доказательство. Пусть событию В благоприятствуют m1, а событию С — m2 элементарных событий группы G. Так как события В и С по условию несовместимы, то элементарные события, благоприятствующие одному из них отличаются от элементарных событий, благоприятствующих другому. Всего, таким образом, имеется m1 + m2 событий, благоприятствующих появлению одного из них, т.е. благоприятствующих появлению события А = В + С. Следовательно,

4. Вероятность события Ā, противоположного событию А равна Доказательство. (свойство 2). Т.к. А и Ā несовместимы, то (свойство 3). Два последних равенства доказывают свойство 4. 5. Вероятность невозможного события равна 0. 6. Если событие А влечет за собой событие В, то р(А)  р(В). Доказательство. Поскольку В = А + ĀВ и события А и ĀВ несовместимы, то 7. Вероятность любого события заключена между нулем и единицей: Доказательство. Для любого события А имеют место соотношения Отсюда, по свойствам 6, 2, 5

3. Основные формулы комбинаторики Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающихся только порядком их расположения. Число всех возможных перестановок n элементов Пример 1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз? Решение. Искомое число трехзначных чисел Запишем все перестановки, которые можно получить из этих цифр: 123, 132, 213, 231, 312, 321.

Размещением из n элементов по m называется любое упорядоченное подмножество из m элементов множества, состоящего из n различных элементов. Число размещений из n элементов по m обозначается Anm и вычисляется по формуле Пример 2. Пусть имеется множество, содержащее четыре буквы {A, B, C, D}. Вычислить число размещений из четырех указанных букв по две. Решение. Искомое число размещений вычислим по формуле Искомыми размещениями будут: AB, AC, AD, BC, BD, CD, BA, CA, DA, CB, DB, DC. Заметим, что размещения отличаются порядком входящих в них элементов и их составом. Размещения AB и BA содержат одинаковые буквы, но порядок их расположения различен. Поэтому эти размещения считаются разными: AB  BA. Если выбор m элементов из множества, состоящего из n элементов, производится с возвращением и упорядочиванием, то получаемые в результате комбинации называются размещениями с повторениями, а их число определяется формулой

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний из n элементов по m обозначается Сnm и вычисляется по формуле Пример 3. Пусть имеется множество, содержащее четыре буквы {A, B, C, D}. Вычислить число сочетаний из четырех указанных букв по три. Решение. Запишем все возможные сочетания из четырех указанных букв по три. Таких сочетаний будет 4: ABC, ACD, ABD, BCD. Здесь в число сочетаний не включены, например, ACB, BCA, так как эти последовательности букв не отличаются от последовательности ABC, поскольку порядок элементов в сочетаниях не учитывается (т.е. AB = BA).

При решении задач из комбинаторики используют следующие правила: Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В — m способами, то выбрать либо А, либо В можно n + m способами. Правило умножения. Если объект А можно выбрать из совокупности объектов n способами и после каждого такого выбора объект В можно выбрать m способами, то пара объектов (А, В) в указанном порядке может быть выбрана n m способами. Пример 4. Из колоды карт (36 карт) наудачу вынимается три карты. а) Найти число комбинаций трех карт, содержащих точно одного туза. б) Найти число комбинаций трех карт, содержащих хотя бы одного туза. Решение. а) Один туз может быть выбран С41 способами, а две другие карты (не тузы) — С322 способами. Общее число комбинаций б) Общее число комбинаций + +

Пример 5. Из колоды карт (36 карт) наудачу вынимается три карты. Найти вероятность того, что среди них окажется а) точно одного туз; б) хотя бы одного туз. Решение. а) Один туз может быть выбран С41 способами, а две другие карты (не тузы) — С322 способами. Общее число таких комбинаций (благоприятных исходов) Полная группа равновероятных и несовместимых событий в нашей задаче состоит из всевозможных комбинаций по 3 карты, их число Искомая вероятность, таким образом, равна б) Общее число комбинаций Искомая вероятность равна Ā

Пример 6. Колода карт (36 карт) наудачу разделяют на две равные части. Найти вероятность того, что в обеих частях окажется по равному числу черных и красных карт. Решение. Общее число различных способов, которыми можно выбрать 18 карт из 36 (общее число исходов) Число способов, которыми можно извлечь 9 красных карт из 18 равно Число способов, которыми можно извлечь 9 черных карт из 18 равно Таким образом, число благоприятствующих исходов а искомая вероятность

4. Относительная частота. Статистическая вероятность Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически проведенных испытаний

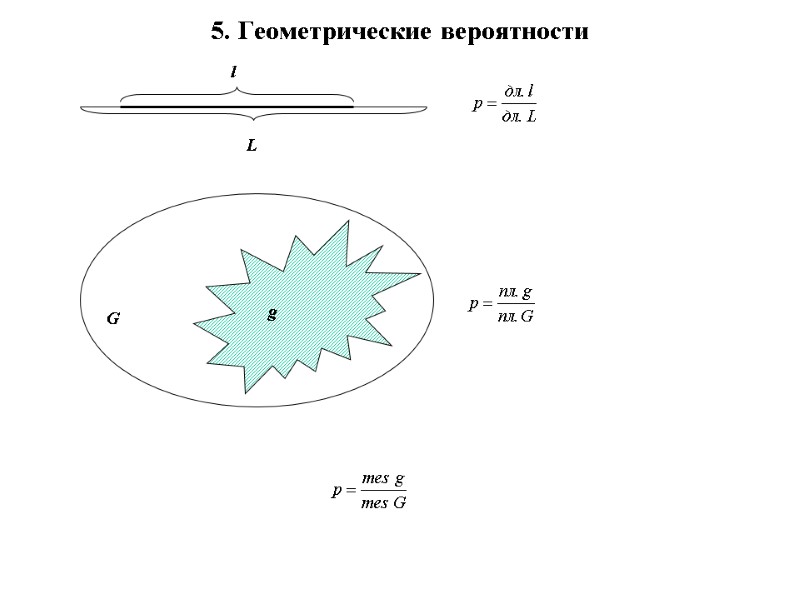
5. Геометрические вероятности

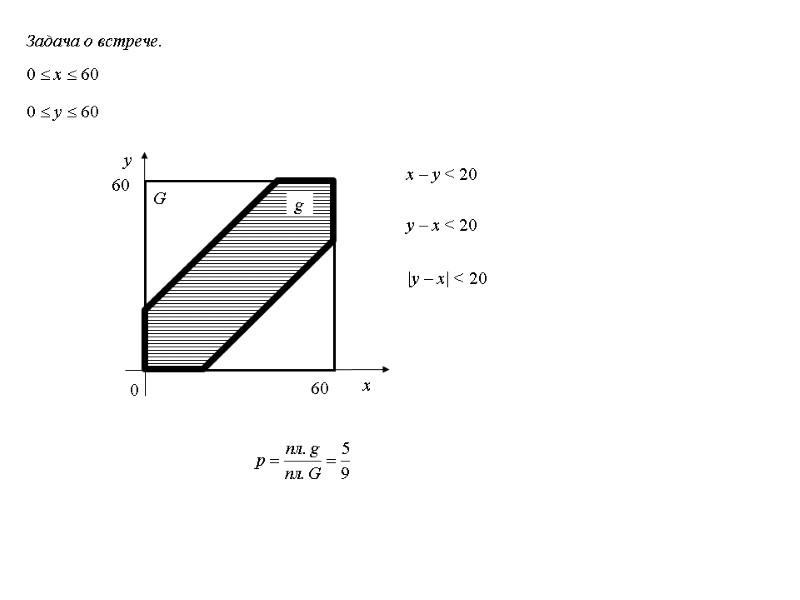
Задача о встрече. 0  x  60 0  y  60 G x – y < 20 y – x < 20 g |y – x| < 20

Теорема умножения вероятностей Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Случайным называется событие, которое при осуществлении определенных условий S может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий S не налагается, то такую вероятность называют безусловной. Если же налагаются другие дополнительные условия, то вероятность называется условной. Например, часто вычисляют вероятность события В при дополнительном условии, что событие А произошло. Условной вероятностью РА(В) называют вероятность события В, вычисленную в предположении, что событие А уже произошло.

Выведем формулу для вычисления условной вероятности РА(В). Пусть имеется n единственно возможных, несовместимых и равновероятных исходов А1, А2, …, Аn, из которых событию А благоприятствует k исходов; событию В благоприятствует m исходов; событию АВ благоприятствует r исходов (r ≤ m; r ≤ k). Если событие A произошло, то это означает, что наступил один из k исходов Aj, благоприятствующих этому событию. При этом событию В благоприятствует только r из указанных событий Aj. Поэтому Аналогично получаем

Каждое из равенств (*), (**) эквивалентно так называемой теореме умножения, согласно которой Следствие Примеры

2. Независимые события. Теорема умножения независимых событий Событие В называется независимым от события А, если появление события А не изменит вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности: Таким образом, Теорема умножения независимых событий Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий. В противном случае события называют зависимыми.

Несколько событий называются независимыми попарно, если независимы любые два из них. Несколько событий называются независимыми в совокупности, если они независимы попарно и независимы каждое из этих событий и всевозможные произведения остальных. Например, события А1, А2, А3, А4 независимы в совокупности, если независимы пары (А1, А2), (А1, А3), (А1, А4), (А2, А3), … а также (А1, А2А3), (А1, А2А4), … (А1, А2А3 А4), … Если n событий А1, А2, …, Аn независимы в совокупности, то вероятность их совместного наступления равна произведению вероятностей этих событий:

3. Вероятность наступления хотя бы одного события Теорема. Вероятность наступления хотя бы одного из А1, А2, …, Аn независимых в совокупности событий равна Доказательство. Обозначим А = {наступило хотя бы одно из событий А1, А2, …, Аn} (не наступило ни одно из Аi) Следствие. Если независимые в совокупности события А1, А2, …, Аn имеют одинаковую вероятность наступления, равную р, то вероятность наступления хотя бы одного из них равна — противоположны,

Следствия из теорем сложения и умножения 1. Теорема сложения вероятностей совместных событий Если А и В — частные случаи, на которые подразделяется некоторое событие С, то Р(С) = Р(А + В) = Р(А) + Р(В). Пусть теперь А и В — совместные события, т.е. появление одного из них не исключает появления другого в одном и том же испытании. Теорема. Вероятность появления хотя бы одного из двух совместных событий равно сумме вероятностей этих событий без вероятности их совместного появления: Р(А + В) = Р(А) + Р(В) – Р(АВ). Доказательство. Поскольку события А и В несовместны, событие А + В наступит, если наступит одно из следующих трех несовместных событий: По теореме сложения вероятностей несовместных событий Событие А произойдет, если наступит одно из двух несовместных событий: По теореме сложения вероятностей несовместных событий откуда Аналогично, Подставляя (**) и (***) в (*), окончательно получаем Р(А + В) = Р(А) + Р(В) – Р(АВ). Замечание. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий Р(А + В) = Р(А) + Р(В) – Р(А)Р(В), для зависимых событий — Р(А + В) = Р(А) + Р(В) – Р(А)РА (В).

2. Формула полной вероятности Теорема. Вероятность события А, которое может наступить при условии появления одного из несовместных событий В1, В2, … Вn , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Доказательство. Событие А может наступить, если наступит одно из несовместных событий В1, В2, … Вn. Другими словами, появление события А означает осуществление одного, безразлично какого из несовместных событий В1А, В2А, … Вn А. По теореме сложения получим Р(А) = Р(В1А) + Р(В2А) + … + Р(Вn А). Подставляя полученные выражения для Р(ВiА) в (*), получим Для каждого из слагаемых в (*) по теореме умножения зависимых событий имеем (*) Замечание. Эту формулу называют формулой полной вероятности.

Пример. В первой коробке содержится 20 микросхем, из которых 18 исправных, во второй коробке — 10 микросхем, из которых 9 исправных. Из второй коробки наудачу взята микросхема и переложена в первую. Найти вероятность того, что микросхема, наудачу извлеченная из первой коробки, окажется исправной. Решение. А = {из первой коробки извлечена исправная микросхема}. Из второй коробки могла быть извлечена исправная микросхема (событие В1), либо неисправная (событие В2). Вероятности этих событий соответственно равны Р(В1) = 9/10, Р(В2) = 1/10.

3. Вероятность гипотез. Формулы Бейеса Пусть событие А может наступить при условии появления одного из несовместных событий В1, В2, … Вn , образующих полную группу. Поскольку заранее неизвестно, какое из событий Вi наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности Так как P(AB) = P(A)PA(B) = P(B)PB(A), то, выражая отсюда условную вероятность PA(B), имеем На основании этого, для любого Bi условная вероятность PA(Bi) того, что событие Bi (гипотеза Bi) имело место вместе с событием A, равна Полученные формулы называют формулами Бейеса. Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Повторение испытаний 1. Формула Бернулли Если проводится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно А. Пусть проводится n независимых испытаний, в каждом из которых событие А может появиться или не появиться. Условимся считать, вероятность события А в каждом испытании одна и та же и равна p. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 – p. Вычислим вероятность того, что при n испытаниях событие А осуществляется k раз и, следовательно, не осуществляется n – k раз. Искомую вероятность обозначим Pn(k). Вероятность одного сложного события, состоящего в том, что в n испытаниях событие А наступит k раз и не наступит n – k раз, по теореме умножения вероятностей независимых событий равна pk qn – k . Количество таких сложных событий равно числу сочетаний из n элементов по k элементов, т.е. Cnk . Таким образом, искомая вероятность Полученная формула называется формулой Бернулли.

Вероятность P того, что в n испытаниях интересующее нас событие появится менее k раз, P(B) = Pn(0) + Pn(1) + … + Pn(k – 1). Вероятность P того, что в n испытаниях событие A появится не более k раз, P(С) = Pn(0) + Pn(1) + … + Pn(k). Вероятность P того, что в n испытаниях событие A появится не менее k раз, P(D) = Pn(k) + Pn(k + 1) + … + Pn(n). Вероятность P того, что в n испытаниях событие A появится более k раз, P(Е) = Pn(k + 1) + Pn(k + 2) + … + Pn(n). Вероятность P того, что в n испытаниях событие A появится хотя бы один раз, P(F) = 1 – Pn(0) = 1 – qn. Если в n испытаниях может появиться одно из k несовместимых событий Ai (i = 1,…,k) и вероятность появления события Ai в каждом испытании равна pi, то вероятность появления в течение n испытаний m1 раз события A1, m2 раз события A2,…, mk раз события Ak (m1 + m2 + … + mk = 1) равна

Вероятности Pn(k), вычисленные по формуле Бернулли при данном n сначала возрастают при увеличении k от 0 до некоторого значения k0, а затем уменьшаются при изменении k от k0 до n, т.е. вероятность Pn(k0) является наибольшей из всех Pn(k). Поэтому k0 называется наивероятнейшим числом наступления события A в n испытаниях. Наивероятнейшее число k0 появления события в n повторных независимых испытаниях — это целое число, заключённое в пределах np – q  k0  np + p, где p — вероятность появления этого события в одном испытании, q — вероятность непоявления этого события в одном испытании. Замечание. Если np – q — целое число, то максимальное значение вероятность Pn (k) принимает для двух значений k, а именно для k0 = np – q и k0′ = np + p. В дальнейшем мы увидим, что с ростом n все вероятности Pn(k) становятся близкими к нулю, но только для k, близких к наивероятнейшему значению k0, вероятности Pn(k) сколько-нибудь заметно отличаются от нуля. Исследуем поведение функции Pn (k) при постоянных n. Для 0 ≤ k ≤ n 1. Pn(k + 1) > Pn(k) при np – q > k; 2. Pn(k + 1) = Pn(k) при np – q = k; 3. Pn(k + 1) < Pn(k) при np – q < k.

2. Локальная теорема Лапласа Для больших значений n и k вычисление вероятности Pn(k) по формуле Бернулли становится весьма трудоёмким, поэтому применяется приближённая формула, выражающая локальную теорему Лапласа. Теорема. Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний n достаточно велико, то вероятность Pn(k) того, что событие A появится в n повторных независимых испытаниях ровно k раз, приближённо равна (тем точнее, чем больше n) значению

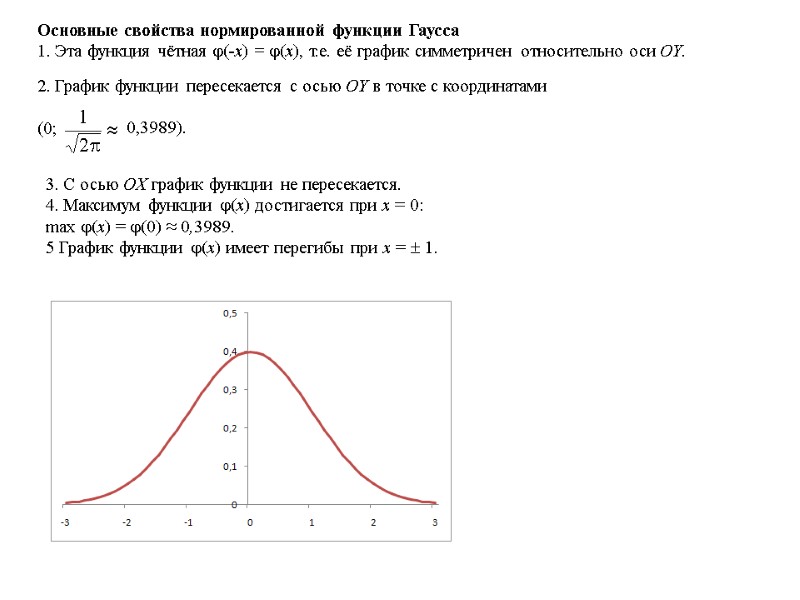
Основные свойства нормированной функции Гаусса 1. Эта функция чётная (‑x) = (x), т.е. её график симметричен относительно оси OY. 3. С осью OX график функции не пересекается. 4. Максимум функции (x) достигается при x = 0: max (x) = (0) ≈ 0,3989. 5 График функции (x) имеет перегибы при x =  1.

3. Формула Пуассона Для редких событий, когда  = np  10, для определения вероятности Pn(k) применяется формула Пуассона. Теорема. Если вероятность p появления события A в каждом испытании постоянна, но мала, число независимых испытаний n достаточно велико, и произведение np =   10, то вероятность Pn(k) того, что событие A появится в n повторных независимых испытаниях ровно k раз, приближённо равна

4. Интегральная теорема Лапласа Теорема. Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Pn(k1  k  k2) того, что событие A появится в n повторных независимых испытаниях не менее k1 и не более k2 раз, приближённо равна определенному интегралу

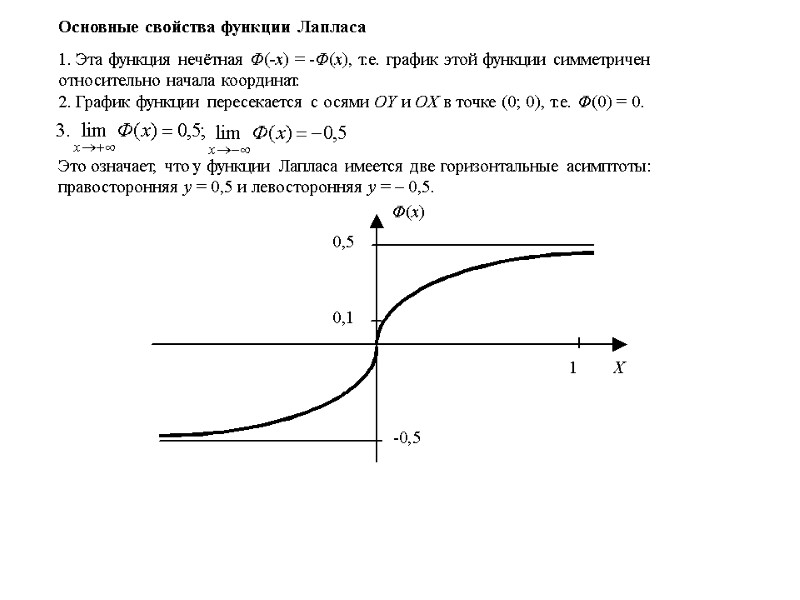
Основные свойства функции Лапласа 1. Эта функция нечётная Ф(‑x) = ‑Ф(x), т.е. график этой функции симметричен относительно начала координат. 2. График функции пересекается с осями OY и OX в точке (0; 0), т.е. Ф(0) = 0. Это означает, что у функции Лапласа имеется две горизонтальные асимптоты: правосторонняя y = 0,5 и левосторонняя y = – 0,5.

4. Закон больших чисел Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то вероятность того, что отклонение относительной частоты m/n от вероятности p по абсолютной величине будет сколь угодно малым приближенно равна Если n велико, то вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым равна 1:

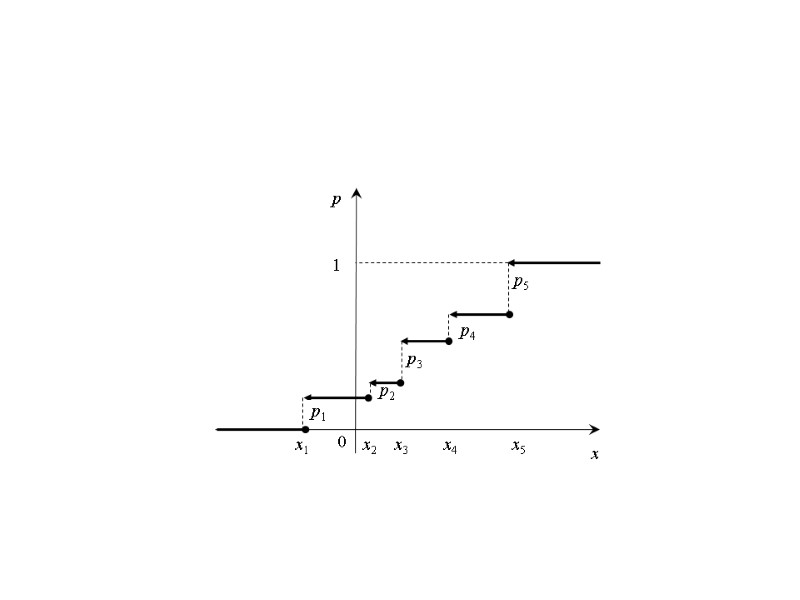
Случайные величины Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных событий, которые заранее не могут быть учтены. Обозначения случайных величин: X, Y, Z; значения — x, y, z. Дискретной (прерывной) называется случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть как конечным, так и бесконечным (счетным). Для задания дискретной случайной величины недостаточно перечислить все ее возможные значения, нужно еще указать их вероятности. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Его можно задать в виде таблицы, аналитически и графически. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения (как правило, в порядке возрастания), а вторая строка — их вероятности. Поскольку в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события X = x1, X = x2, …, X = xk, образуют полную группу, следовательно, сумма вероятностей этих событий равна единице: Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (xi , pi), а затем соединяют их отрезками прямых. Полученная фигура называется многоугольник распределения.

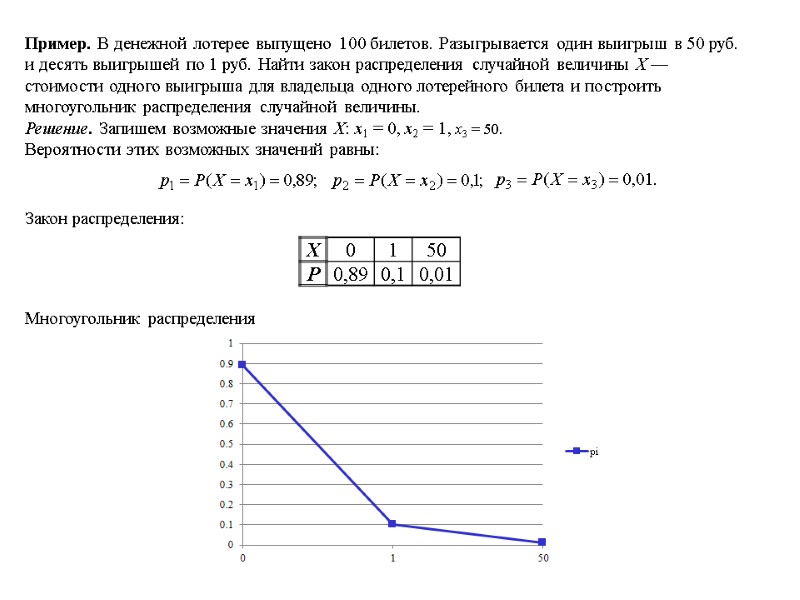
Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X — стоимости одного выигрыша для владельца одного лотерейного билета и построить многоугольник распределения случайной величины. Решение. Запишем возможные значения Х: х1 = 0, х2 = 1, х3 = 50. Вероятности этих возможных значений равны: Закон распределения: Многоугольник распределения

Пусть задана дискретная случайная величина Х Произведение постоянной величины С на дискретную случайную величину Х есть дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значений Х: Две случайные величины Х и Y называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая величина; в противном случае они называются зависимыми. Произведением независимых случайных величин Х и Y называется случайная величина ХY , возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y; вероятности возможных значений ХY равны произведениям вероятностей возможных значений сомножителей Суммой случайных величин Х и Y называется случайная величина Х + Y , возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; вероятности возможных значений Х + Y равны произведениям вероятностей слагаемых для независимых величин и произведениям вероятности одного слагаемого на условную вероятность другого для зависимых величин

Числовые характеристики дискретных случайных величин Математическое ожидание дискретной случайной величины Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех ее возможных значений на соответствующие вероятности Замечание. Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. Пример 1. Найти математическое ожидание дискретной случайной величины, зная закон ее распределения: Решение. По определению имеем Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р. Решение. Случайная величина Х — число появлений события А в одном испытании — может принимать только два значения: x1 = 1 с вероятностью р и x2 = 0 с вероятностью q = 1 – р. Искомое математическое ожидание M(Х) = 1 * р + 0 * q = р.

Вероятностный смысл математического ожидания Пусть проведено n испытаний, в которых случайная величина Х приняла m1 раз значение х1, m2 раз значение х2, …, mk раз значение хk, причем m1 + m2 + … + mk = n. Тогда сумма всех значений, принятых Х равна m1х1 + m2 х2 + … + mkхk. Среднее арифметическое всех значений, принятых этой случайной величиной Заметим, что mi/n = wi — относительной частоте значения хi. Допустим, что число испытаний велико. Тогда wi ≈ pi. Заменяя в последнем выражении относительные частоты вероятностями, получим Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины. Замечание.

Свойства математического ожидания 1. Математическое ожидание постоянной величины С равно самой постоянной: М(С) = С. Доказательство. Рассмотрим постоянную величину С как дискретную случайную величину, которая имеет одно возможное значение С и принимает его с вероятностью р = 1. Следовательно, М(С) = С ∙ 1 = С. 2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = С ∙ М(Х). Доказательство. 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: М(ХY) = М(Х) ∙ М(Y). Доказательство.

4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: М(Х + Y) = М(Х) + М(Y). Доказательство. Докажем, что р11 + р12 = р1. Событие {Х = х1}влечет за собой событие {Х + Y = (х1 + y1 или х1 + y1)} и обратно Аналогично,

Дисперсия дискретной случайной величины Пусть Х — случайная величина и М(Х) — ее математическое ожидание. Отклонением называют случайную величину Х - М(Х) , возможные значения которой равны разностям между возможными значениями случайной величины и ее математическим ожиданием, а вероятности величины Х - М(Х) равны вероятностям величины Х. Теорема. Математическое ожидание отклонения равно 0: М[Х - М(Х) ] = 0. Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Пример. Найти дисперсию случайной величины Х, заданной законом распределения Решение. Математическое ожидание: М(Х) = 1 ∙ 0,3 + 2 ∙ 0,5 + 5 ∙ 0,2 = 2,3. Все возможные значения квадрата отклонения: [x1 – M(X)]2 = (1 – 2,3) 2 = 1,69; [x2 – M(X)]2 = (2 – 2,3) 2 = 0,09; [x3 – M(X)]2 = (5 – 2,3) 2 = 7,29. Закон распределения квадрата отклонения Дисперсия: D(X) = 1,69 ∙ 0,3 + 0,09 ∙ 0,5 + 7,29 ∙ 0,2 = 2,01.

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: D(X) = М(Х 2) – [М(Х)]2. Доказательство. Поскольку математическое ожидание М(Х) — есть величина постоянная, то 2 М(Х) и [М(Х)]2 — также постоянные величины. Поэтому = М(Х 2) – [М(Х)]2. Пример. Найти дисперсию случайной величины Х, заданной законом распределения Решение. Математическое ожидание: М(Х) = 1 ∙ 0,3 + 2 ∙ 0,5 + 5 ∙ 0,2 = 2,3. Закон распределения квадрата случайной величины Математическое ожидание квадрата случайной величины: М(Х) = 1 ∙ 0,3 + 4∙ 0,5 + 25 ∙ 0,2 = 7,3. Дисперсия: D(X) = 7,3 – 2,32 = 2,01.

1. Дисперсия постоянной величины С равна нулю: D(С) = 0. 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX) = C2D(X). 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X + Y) = D(X ) + D(Y). 4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин: D(X - Y) = D(X ) + D(Y).

Среднее квадратическое отклонение Дисперсия имеет размерность квадрата случайной величины. Для того чтобы иметь показатель рассеяния случайной величины той же размерности, что и размерность случайной величины, извлекают корень квадратный из дисперсии. Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин

Одинаково распределенные взаимно независимые числовые величины Рассмотрим n взаимно независимых случайных величин X1, X2, …, Xn, которые имеют одинаковые распределения и, следовательно, и одинаковые характеристики. Установим соответствие между характеристиками среднего арифметического и соответствующими характеристиками каждой отдельной величины. 1. Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой величины: 2. Дисперсия среднего арифметического одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин: 3. Среднее квадратическое отклонение среднего арифметического одинаково распределенных взаимно независимых случайных величин в раз меньше среднего квадратического отклонения  каждой из величин: Обозначим среднее арифметическое этих величин

Начальные и центральные теоретические моменты Начальным моментом порядка k случайной величины Х называют математическое ожидание величины X k : В частности, и т.д. Центральным моментом порядка k случайной величины Х называют математическое ожидание величины (Х – М (X))k : В частности,

Примеры 1. Пусть проводится n независимых испытаний, в каждом из которых событие A может появиться или не появиться; вероятность наступления события А во всех испытаниях постоянна и равна р (соответственно вероятность непоявления q = 1 – р). Рассмотрим в качестве дискретной случайной величины Х число появления события А в этих испытаниях. Поставим задачу: найти закон распределения величины Х. х1 = 0, х2 = 1, х3 = 2, хn + 1 = n. …, Распределение вероятностей, определяемое формулой Бернулли, называется биноминальным Математическое ожидание М(Х) числа появлений события А в n независимых испытаниях М(Х) = np, дисперсия D(X) = npq. 2. Пусть проводится n независимых испытаний, в каждом из которых вероятность наступления события А равна р, причем n велико, а р мало. Вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события мала, событие наступит k раз вычисляется по формуле Пуассона Распределение вероятностей, определяемое формулой Пуассона, называется распределением Пуассона. Математическое ожидание М(Х) и дисперсия D(X) числа появлений события А для распределения Пуассона М(Х) = D(X) =  ( = np)

3. Пусть из урны, содержащей n шаров, m из которых — белые, случайным образом отбирают (без возвращения) s шаров. Количество белых шаров среди отобранных есть случайная величина Х, возможные значения которой 0, 1, 2, …, min(M, s). Найдем вероятность Р(Х = k) того, что среди s отобранных шаров k — белые. Число способов отобрать s шаров из n — при этом число способов отбора белых шаров — не белых шаров — Искомая вероятность Распределение вероятностей, определяемой формулой (*), называется гипергеометрическим. (*)

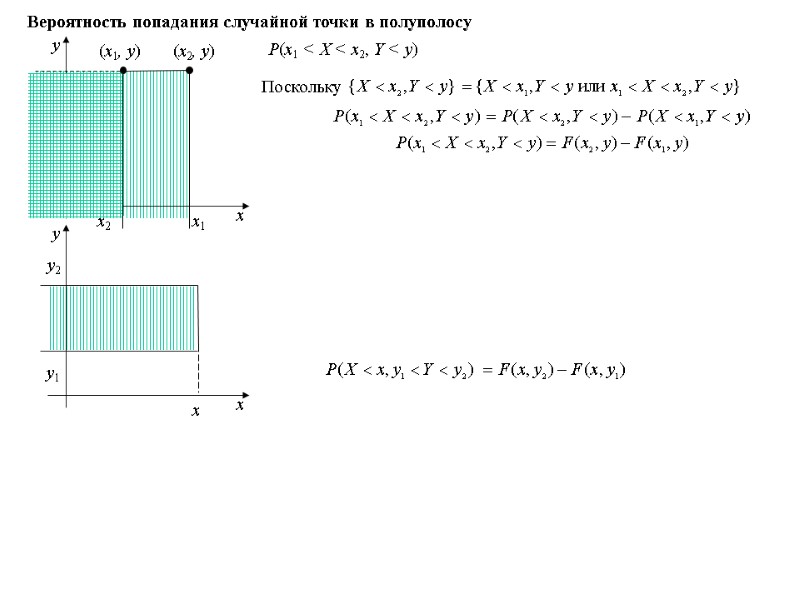
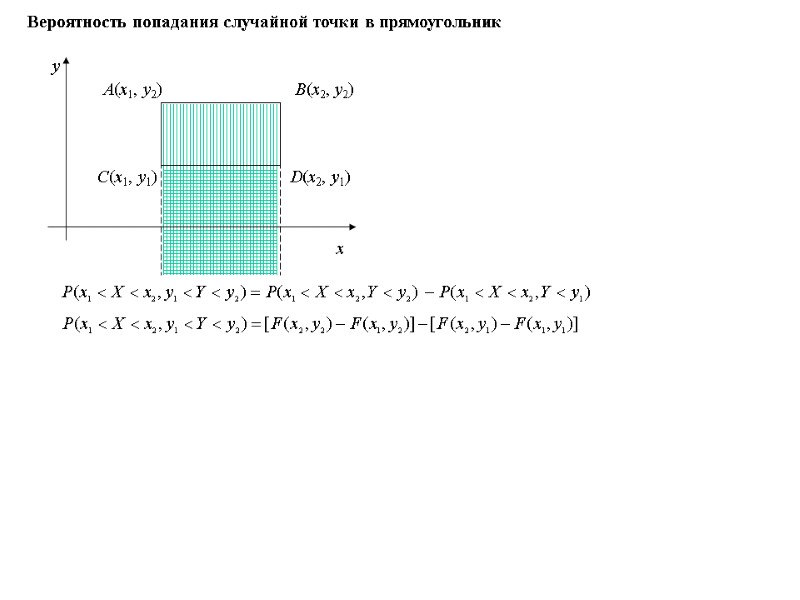
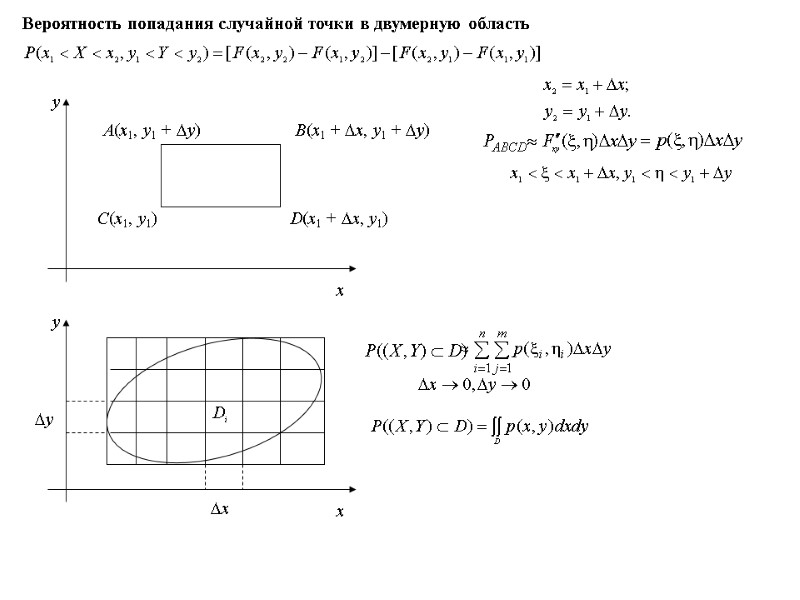
Функция распределения Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е. F(x) = P(X < x). Свойства функции распределения 1. Значения функции распределения принадлежат отрезку [0; 1]: 0 ≤ F(x) ≤ 1. 2. Функция распределения непрерывна слева. 3. F(x) — неубывающая функция, т.е. F(x1) ≤ F(x2), если x1 < x2. Доказательство. Пусть x1 < x2. {X < x2} = {X < x1 и x1 ≤ X < x2}  P(X < x2) = P(X < x1) + P(x1 ≤ X < x2)  P(X < x2) - P(X < x1) = P(x1 ≤ X < x2)  F(x2) – F(x1) = P(x1 ≤ X < x2) Итак, каждая функция распределения является неубывающей, непрерывной слева и удовлетворяющей условиям F(-) = 0, F(+) = 1. Верно и обратное: каждая функция, удовлетворяющая указанным условиям, может рассматриваться как функция распределения некоторой случайной величины. Поскольку P(x1 ≤ X < x2) ≥ 0, то  F(x1) ≤ F(x2) 4. (**)

Для дискретной случайной величины, заданной законом распределения функция распределения F(х) задается равенством Таким образом, функция распределения дискретной случайной величины является ступенчатой функцией со скачками высотой pi в точках xi. Пример. Дискретная случайная величина Х задана таблицей распределения Найти функцию распределения и построить ее график. Решение. F(x) = P(X < x). F(x) = при х ≤ 1 0 при 1 < х ≤ 4 0,3 при 4 < х ≤ 6 0,9 при 6 < х 1 ={X = 1 или Х = 4} {X < x} 0,3 0,9 1 ={X = 1} {X < x} {X < x} {X < x} — невозможное событие — достоверное событие

Свойства функции распределения непрерывной случайной величины 1. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение равно 0. Доказательство. Положим в (**) x2 = x1 + x. Тогда P(x1 ≤ X < x1 + x) = F(x1 + x) – F(x1). Пусть x  0. Тогда, в силу непрерывности F(x) F(x1 + x) – F(x1)  0  P(X = x1) = 0. P(a ≤ X < b) = P(a < X < b) = P(a < X ≤ b) = P(a ≤ X ≤ b). 2. Если возможные значения непрерывной случайной величины принадлежат интервалу (a, b), то а) F(x) = 0 при x ≤ a; б) F(x) = 1 при b ≤ x. Случайная величина называется непрерывной, если существует неотрицательная функция р(х), удовлетворяющая при любых х равенству Функция р(х) называется плотностью распределения вероятностей. Если F(x) абсолютно непрерывна, а тем более, дифференцируема при всех х, то ее производная и является плотностью распределения: Функция распределения иногда называется интегральной, а плотность — дифференциальной функцией распределения. Непрерывная случайная величина Если возможные значения случайной величины принадлежат интервалу [a, b], то Если возможные значения случайной величины принадлежат всей числовой оси, то

Вероятность попадания непрерывной случайной величины в заданный интервал Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b: Доказательство. По формуле Ньютона-Лейбница Таким образом, Поскольку P(a ≤ X < b) = P(a < X < b), то Воспользуемся соотношением (**): P(a ≤ X < b) = F(b) – F(a)

Числовые характеристики непрерывных случайных величин Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат интервалу [a, b], называют определенный интеграл Если возможные значения случайной величины принадлежат всей числовой оси, то (предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения случайной величины принадлежат интервалу [a, b], то Если возможные значения случайной величины принадлежат всей числовой оси, то Среднее квадратическое отклонение непрерывной случайной величины Замечание.

Медианой непрерывной случайной величины называется такое ее значение m, при котором F(m)=0,5; другими словами, Квантилью порядка р (0 < р < 1) называется корень уравнения F(х) = р. Если случайная величина непрерывна, то модой распределения называют то значение аргумента, при котором плотность достигает максимума. Модой дискретной случайной величины называют ее наиболее вероятное значение.

Равномерное распределение вероятностей Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное отличное от нуля значение: Замечание. Числовые характеристики равномерно распределенной случайной величины

Нормальное распределение Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью Нормальное распределение определяется двумя параметрами: а и .

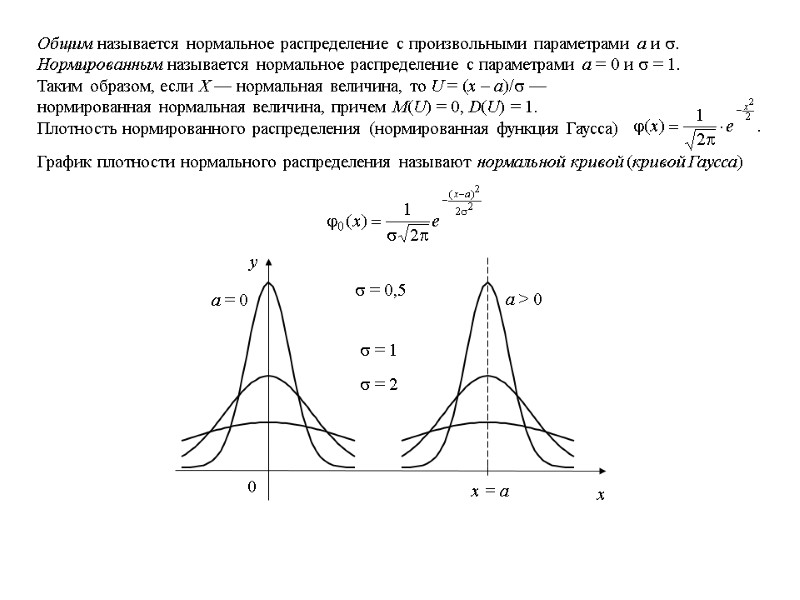
Общим называется нормальное распределение с произвольными параметрами а и . Нормированным называется нормальное распределение с параметрами а = 0 и  = 1. Таким образом, если Х — нормальная величина, то U = (х – а)/ — нормированная нормальная величина, причем M(U) = 0, D(U) = 1. Плотность нормированного распределения (нормированная функция Гаусса) График плотности нормального распределения называют нормальной кривой (кривой Гаусса)  = 2  = 1  = 0,5 a = 0 a > 0

1. Функция F0(x) общего нормального распределения и функция F(х) нормированного распределения связаны соотношением 2. Вероятность попадания нормированной нормальной величины Х в интервал (0, х) вычисляется при помощи функции Лапласа: 3.

Вероятность попадания в заданный интервал нормальной случайной величины

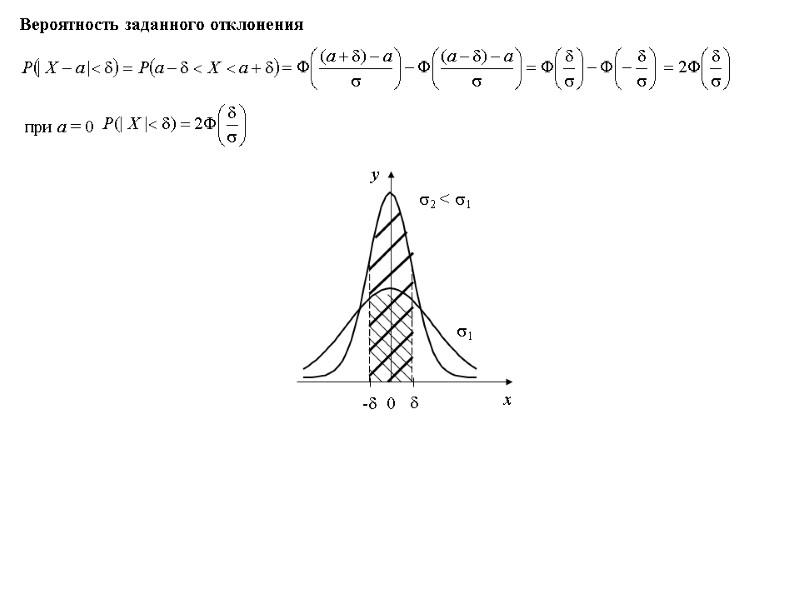
Вероятность заданного отклонения 1 2 < 1 при а = 0

Правило «трех сигм»

Вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение очень мала, а именно равна 0,0027. Это означает, что такое может произойти лишь в 0,27% случаев. Такие события исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

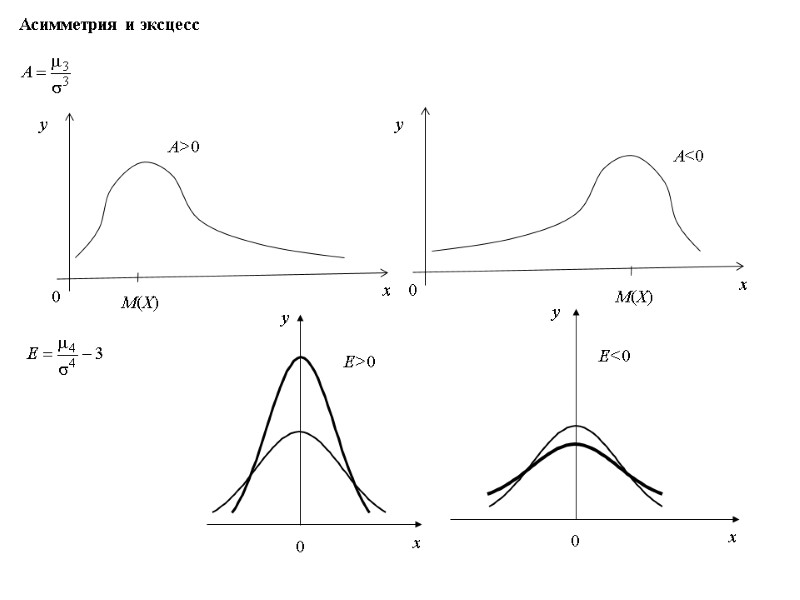
Асимметрия и эксцесс E>0 E<0

При изучении распределений, отличных от нормального, возникает необходимость качественно оценить это различие. С этой целью вводят специальные числовые характеристики, в частности, асимметрию и эксцесс. Для нормального распределения эти характеристики равны нулю. Поэтому небольшие значения асимметрии и эксцесса дают возможность предположить, что такое распределение близко к нормальному; большие значения указывают на значительное отклонение от нормального распределения. Можно показать, что для симметричных распределений каждый центральный момент нечетного порядка равен нулю. Для несимметричных распределений такие моменты отличны от нуля. Поэтому центральный момент третьего порядка используется для оценки асимметрии. Асимметрия положительна, если более пологая часть кривой распределения расположена справа от математического ожидания и отрицательна, если слева. Для оценки «крутизны» подъема распределения по сравнению с нормальным используется характеристика, называемая эксцессом. Если эксцесс больше нуля, то кривая такого распределения имеет более высокую и острую вершину, чем нормальная кривая, если эксцесс меньше нуля, то сраниваемая кривая имеет более низкую и плоскую вершину, чем нормальная.

Показательное распределение Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью Функция распределения показательного закона:

Вероятность попадания в заданный интервал показательно распределенной случайной величины Учитывая, что при х ≥ 0 Воспользуемся формулой P(a < X < b) = F(b) – F(a). получаем Числовые характеристики показательного распределения Пусть случайная величина Х распределена по показательному закону Математическое ожидание Дисперсия Среднее квадратическое отклонение

Показательный закон надёжности Пусть некоторое устройство начинает работать в некоторое время t0 = 0, а спустя время t происходит отказ. Обозначим через Т непрерывную случайную величину — длительность безотказной работы устройства. Если устройство проработало безотказно время, меньшее t, то, следовательно, за период времени t наступит отказ. Функция распределения F(t) = P(T < t ) определяет вероятность отказа за время длительностью t. Следовательно, вероятность безотказной работы устройства за время t, т.е. вероятность противоположного события T > t равна R(t) = P(T > t ) = 1 - F(t). Функцией надежности R(t) называют функцию, определяющую вероятность безотказной работы устройства за время t : R(t) = P(T > t ). Нередко длительность времени безотказной работы устройства имеет показательное распределение с функцией распределения F(t) = 1 – e -t, то функция надежности в случае показательного распределения времени безотказной работы устройства имеет вид ( — интенсивность отказов) Характеристическое свойство показательного закона надёжности Пусть времени безотказной работы устройства имеет показательное распределение.. Тогда вероятность безотказной работы устройства на интервале длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t (при заданной интенсивности отказов ).

Функция одного случайного аргумента и ее распределение Если каждому возможному значению случайной величины Х соответствует одно и только одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х: Y = (X). 1. Пусть Х — дискретная случайная величина. а) Если различным возможным значениям Х соответствуют различные возможные значения Y, то вероятности соответствующих значений Х и Y равны между собой. Пример. Дискретная случайная величина Х задана законом распределения Найти функцию распределения Y = X2. Решение. Возможные значения случайной величины Y: Закон распределения случайной величины Y: б) Если различным возможным значениям Х соответствуют значения Y, среди которых есть равные между собой, то вероятности повторяющихся значений Y складываются. Пример. Дискретная случайная величина Х задана законом распределения Найти функцию распределения Y = X2. Решение. P(Y = 4) = P(X = -2 или Х = 2) = 0,3 + 0,1 = 0,4; Р(Y = 9) = Р(Х = 3) = 0,6.

2. Пусть X — непрерывная случайная величина, p(x) — плотность, Y = (X) — функция этой случайной величины. Если y = (х) — дифференцируемая строго возрастающая или строго убывающая функция, обратная функция которой х = (y), то плотность распределения g(y) случайной величины Y находится с помощью равенства Пример. Случайная величина X распределена по нормальному закону, причем а = 0. Найти распределение случайной величины Y = X3. Решение. Так как функция y = x3 дифференцируема и строго возрастает, то обратная к ней функция имеет вид (y) = y 1/3. Поскольку

Числовые характеристики функции одного случайного аргумента Пусть задана функция Y = (X) случайного аргумента Х. 1. Пусть Х — дискретная случайная величина. Y — также является дискретной случайной величиной 2. Пусть X — непрерывная случайная величина, p(x) — плотность, Y = (X) — функция этой случайной величины.

Распределение суммы независимых слагаемых Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y: Z = (X, Y). Рассмотрим распределение суммы независимых слагаемых: Z = X+ Y. 1. Пусть X и Y — дискретные независимые случайные величины. Для того, чтобы составить закон распределения Z = X+ Y, надо найти все возможные значения Z и их вероятности. Пример. Дискретные независимые случайные величины заданы распределениями Составить закон распределения случайной величины Z = X+ Y. Решение.

2. Пусть X и Y — непрерывные независимые случайные величины. Если X и Y независимы, то плотность распределения g(z) суммы Z = X + Y (при условии, что плотность распределения хотя бы одного из аргументов задана на интервале (-, ) одной формулой) может быть найдена при помощи равенства где f 1, f 2 — плотности распределения аргументов. Плотность распределения суммы независимых случайных величин называют композицией.

Система двух случайных величин Закон распределения двумерной случайной величины Кроме одномерных случайных величин изучают случайные величины, возможные значения которой определяются двумя, тремя, …, n числами. Такие величины называют соответственно двумерными, трехмерными, и т.д. Двумерную случайную величину будем обозначать (X, Y ). Каждую из величин X, Y называют составляющей (компонентой) двумерной случайной величины. Аналогично n-мерная случайная величина определяется как система n случайных величин.

Закон распределения двумерной случайной величины Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, т.е. пар (xi, yj) и их вероятностей pij = p (xi, yj) (i = 1, …, n; j = 1, …, m). Обычно закон распределения двумерной дискретной случайной величины задают в виде таблицы. P(X = xi) P(Y = yj) ∑ ∑ p(xi, yj) = 1 ∑ P(X = xi) = 1 ∑ P(Y = yj) = 1 События {X = xi, Y = yj} образуют полную группу Событие {X = x1} = ({X = x1; Y = y1} или {X = x1; Y = y2} … или {X = x1; Y = ym} )

Функция распределения двумерной случайной величины Рассмотрим двумерную случайную величину (X, Y) (дискретную или непрерывную). Функцией распределения двумерной случайной величины (X, Y) называют функцию F (x, y), определяющую для каждой пары чисел (x, y) вероятность того, что X примет значение, меньшее x, Y примет значение меньше y: F (x, y) = P (X < x, Y < y) Пример. Найти Р(Х < 2, Y < 3). Решение. Свойства функции распределения двумерной случайной величины 1. 0 ≤ F (x, y) ≤ 1. 2. F (x2, y) ≥ F (x1, y), если x2 ≥ x1; F (x, y2) ≥ F (x, y1), если y2 ≥ y1. 3. F(-∞, y) = 0; F(x, -∞) = 0; F(-∞, -∞) = 0; F(∞, ∞) = 1. 4. F(x, ∞) = F1 (x); F(∞, y) = F2 (y).

Вероятность попадания случайной точки в полуполосу P(x1 < X < x2, Y < y) Поскольку

Вероятность попадания случайной точки в прямоугольник

Плотность совместного распределения вероятностей двумерной случайной величины Будем предполагать, что функция распределения F(x, y) непрерывна и имеет почти всюду непрерывные частные производные второго порядка. Плотностью совместного распределения вероятностей p(x, y) двумерной непрерывной случайной величины называют вторую смешанную производную от функции распределения: Зная плотность совместного распределения, можно найти функцию распределения F(x, y) по формуле

Вероятность попадания случайной точки в двумерную область

Свойства двумерной плотности вероятности Двумерная плотность вероятности неотрицательна: p(x, y) ≥ 0. 2. Отыскание плотностей вероятности составляющих двумерной случайной величины Пусть известна плотность совместного распределения вероятностей системы двух случайных величин p(x, y). Найдем плотность распределения составляющей X. Обозначим через F1(x) функцию распределения составляющей Х. По определению плотности распределения одномерной случайной величины Плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей.

Условные законы распределения составляющих системы дискретных случайных величин Для того чтобы охарактеризовать зависимость между составляющими случайной величины, введем понятие условного распределения. Рассмотрим дискретную двумерную случайную величину (X, Y). Пусть возможные значения составляющих таковы: x1, x2, …, xn, y1, y2, …, ym. Допустим, что в результате испытания величина Y приняла значение yj: Y = yj; при этом Х примет одно из возможных значений x1, или x2, … или xn. Обозначим p(xi | yj) вероятность того, что случайная величина Х примет значение xi, при условии, что Y = yj. Эта вероятность, вообще говоря, не будет равна безусловной вероятности p(xi). Условным распределением составляющей X при Y = yj называют совокупность условных вероятностей p(x1 | yj), p(x2 | yj), …, p(xn | yj), вычисленных в предположении, что событие {Y = yj} уже наступило. Аналогично определяется условное распределение составляющей Y. Зная закон распределения двумерной случайной величины, можно, пользуясь формулой условной вероятности, вычислить условные законы распределения составляющих. Например, условный закон распределения X, в предположении, что событие Y = yj уже произошло, может быть найден по формуле Аналогично, условные законы распределения составляющей Y: Замечание. Сумма вероятностей условного распределения равна 1: при фиксированном yj при фиксированном xi

Пример. Дискретная двумерная случайная величина задана следующим законом распределения 0,60 0,40 P(Y = yj) Найти условные законы распределения составляющей X. Решение. Найдем закон распределения составляющей Y: Далее, по формуле

Условные законы распределения составляющих системы непрерывных случайных величин Пусть (X, Y) — непрерывная случайная величина. Условной плотностью (x | y) распределения составляющей X при данном значении Y = y называют отношение плотности совместного распределения p(x, y) системы (X, Y) к плотности распределения pY(y) составляющей Y: Если известна плотность совместного распределения p(x, y), то условные плотности составляющих могут быть вычислены по формулам Умножая безусловный закон распределения одной из составляющих на условный закон распре- деления другой составляющей, найдем закон распределения системы случайных величин: Свойства: Отличие условной плотности (x | y) от безусловной pX(x) состоит в том, что функция (x | y) дает распределение Х при условии Y = y; функция pX (x) дает распределение х независимо от того, какие из возможных значений приняла составляющая Y. Аналогично определяется условная плотность составляющей Y при данном значении Х = х:

Пример. Двумерная случайная величина (X, Y) задана плотностью совместного распределения Найти условные законы распределения составляющих. Решение. При

Условное математическое ожидание Условным математическим ожиданием дискретной случайной величины Y при X = x (x — определенное возможное значение Х) называют сумму произведений возможных значений Y на их условные вероятности: Для непрерывных величин где (y | x) — условная плотность случайной величины Y при X = x . Условное математическое ожидание M(Y | x) есть функция от х: M(Y | x) = f(x), которую называют функцией регрессии Y на X. Аналогично определяется условное математическое ожидание случайной величины Х и функция регрессии Х на Y: M(Х | y) = (y).

Пример. Задана двумерная случайная величина: Найти условное математическое ожидание составляющей Y при х1 = 1. Решение. Найдем условное распределение вероятностей величины Y при Х = 1:

Зависимые и независимые случайные величины. Две случайные величины X и Y называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Условные распределения независимых величин равны их безусловным распределениям. Теорема 1. Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы функция распределения системы (X , Y) была равна произведению функций распределения составляющих: F(x, y) = F1 (x) F2 (y). Теорема 2. Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы (X , Y) была равна произведению плотностей распределения составляющих: p(x, y) = pХ (x) pY (y).

Корреляционный момент. Коэффициент корреляции. Корреляционным моментом xy случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: Теорема 2. Корреляционный момент служит для характеристики связи между величинами X и Y . Теорема 1. Корреляционный момент двух независимых случайных величин X и Y равен нулю. Доказательство. Коэффициентом корреляции rxy случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин Замечание. Пусть дана случайная величина Х. Теорема 3. |rxy| ≤ 1. Нормированная случайная величина Для двух случайных величин X и Y

Коррелированность и зависимость случайных величин Две случайные величины X и Y называют коррелированными, если их коэффициент корреляции (или корреляционный момент) отличен от нуля; случайные величины X и Y называют некоррелированными, если их корреляционный момент равен 0. Две коррелированные величины также зависимы. Обратное предположение не верно, т.е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Пример. Двумерная случайная величина (X, Y) задана плотностью распределения Доказать, что X и Y — зависимые некоррелированные величины. Решение. Вычислим плотности распределения составляющих (внутри эллипса)  X и Y — зависимые величины Поскольку pX(x) и pY(y) симметричны относительно Ох и Oy, то M(X) = M(Y) = 0.  X и Y — некоррелированные величины

Нормальный закон распределения на плоскости Нормальным законом распределения на плоскости называют распределение вероятностей двумерной случайной величины, определяемое плотностью Нормальный закон на плоскости задается пятью параметрами: а1, а2 — математические ожидания; x, y — средние квадратические отклонения; rxy — коэффициент корреляции величин Х и Y. Положив rxy = 0, получим Таким образом, видим, что если составляющие нормально распределенной случайной величины некоррелированы (rxy = 0), то ее составляющие — независимы [f(x, y) = fX(x) fY(y)]. Можно показать, что если двумерная случайная величина распределена по нормальному закону, то и ее составляющие также распределены но нормальному закону.

Линейная регрессия. Прямые линии среднеквадратической регрессии. Рассмотрим двумерную случайную величину (X, Y), где X, Y — зависимые случайные величины. Поставим задачу представить одну из этих величин как функцию другой Y  g(X). Одним из способов отыскания g(X) является метод наименьших квадратов: g(X) наилучшим образом приближает Y в смысле метода наименьших квадратов, если M[Y - g(X)]2 принимает наименьшее значение; g(X) называют среднеквадратической регрессией Y на X. Будем искать g(X) в виде g(X) = Х + , где  и  — параметры, подлежащие определению (в этом случай g(X) называют линейной среднеквадратической регрессией Y на X). F(, )=M[Y - X - ]2  min.

Линейная средняя квадратическая регрессия Y на X имеет вид где — коэффициент регрессии Y на X, — прямая среднеквадратической регрессии Y на Х. — остаточная дисперсия случайной величины Y относительно Х, которая характеризует величину ошибки при замене Y линейной функцией g(X) = Х + . При r = ±1 остаточная дисперсия равна 0. Другими словами, при r = ±1 Y и Х связаны линейной зависимостью. Прямая среднеквадратической регрессии Х на Y имеет вид Здесь — коэффициент регрессии X на Y, — остаточная дисперсия случайной величины X относительно Y. Если r = ±1, то обе прямые регрессии совпадают. Обе прямые регрессии проходят через точку (mx; my), которая называется центром совместного распределения X и Y.