ТЕОРИЯ ВЕРОЯТНОСТЕЙ Основные понятия и теоремы Преподаватель Шилова

ТЕОРИЯ ВЕРОЯТНОСТЕЙ Основные понятия и теоремы Преподаватель: Шилова З. В.

Цели Знакомство с новыми понятиями и математическими фактами теории вероятностей, установление между ними взаимосвязей. 2. Воспитание познавательного интереса к теории вероятностей, воспитание культуры мышления. 3. Развитие умения переноса знаний на новую ситуацию, развитие способности анализировать, сопоставлять вероятностные факты. 1.

План лекции 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Введение. Исторический аспект. События. Классификация событий. Действия над событиями. Вероятность. Свойства вероятности. Основные теоремы вероятности. Список рекомендуемой литературы. Домашнее задание. Подведение итогов.

Введение q Теория вероятностей - математическая наука, изучающая закономерности, присущие массовым случайным явлениям. q Предмет теории вероятностей – математические модели случайных явлений. q Цель теории вероятностей – осуществление прогноза в области случайных явлений, влияние на ход этих явлений, контроль их, ограничение сферы действия случайности.

Исторический аспект q Теория вероятностей возникла в середине XVII в. в связи с задачами расчета шансов выигрыша игроков в азартных играх. q Первые работы по теории вероятностей принадлежат Б. Паскалю, П. Ферма, Х. Гюйгенсу и др. Блез Паскаль (19. 6. 1623, Клермон. Ферран, - 19. 8. 1662, Париж), французский религиозный философ, писатель, математик и физик. Родился в семье высокообразованного юриста

КАК РАССУЖДАЛ ПАСКАЛЬ? q Игральная кость представляет собой правильный кубик, на шести гранях которого нанесены цифры 1, 2, 3, 4, 5 и 6 (число очков). Если бросить кость «наудачу» , то может выпасть любое число очков (от 1 до 6). Это явление носит случайный характер.

События. Классификация событий Испытанием, или опытом, называют всякое осуществление определенного комплекса условий или действий, при которых происходит соответствующее явление. Результат (исход) испытания называется событием. Пример. Испытание: подбрасывание монеты Событие: выпадение герба или цифры на верхней стороне монеты

Пример q Стрелок стреляет по мишени. q Выстрел – это испытание. q Попадание в мишень – событие.

Пример q В урне имеются цветные шары. Из урны наудачу берут один шар. q Извлечение шара из урны – это … q … – это событие.

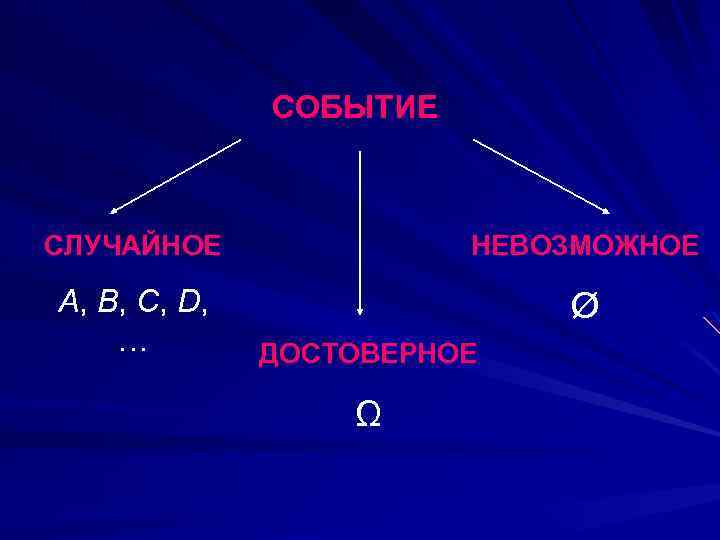СОБЫТИЕ СЛУЧАЙНОЕ НЕВОЗМОЖНОЕ A, B, C, D, … Ø ДОСТОВЕРНОЕ Ω

Случайным событием называют событие, которое в данном испытании может либо произойти, либо не произойти. Пример. Попадание молнии в дерево.

Достоверным называют такое событие, которое обязательно наступит в результате данного испытания. Пример. Заход Солнца в средних широтах.

Невозможным называют событие, которое в данном испытании (в данных условиях) произойти не может. Пример. Свободный полет (левитация) человека в условиях Земли.

Пример Стрелок производит один выстрел по мишени, разделенной на 10 зон. Выстрел – это … Попадание в «десятку» – это событие … Событие, состоящее в том, что мишень либо поражена, либо не поражена – это событие… Поражение одним выстрелом сразу трёх зон – это событие …

q Два события называются совместными, если появление одного из них не исключает появление другого. Пример. Получение оценок «отлично» и «хорошо» на экзаменах по двум дисциплинам. q Два события называются несовместными, если появление одного из них исключает появление другого. Пример. Выигрыш по одному лотерейному билету двух ценных предметов.

q Два события называются зависимыми, если появление одного из них влечёт появление другого. Пример. Вынуть чёрный шар из урны, если из неё уже был предварительно вынут шар. q Два события называются независимыми, если появление одного из них не влечёт появление другого. Пример. Выпадение орла при двукратном бросании монеты.

q Если два события в результате данного испытания обязательно должны произойти, но наступление одного из них исключает наступление другого, то такие события называются противоположными А и Ā. Пример. Условие – в семье родился один ребёнок. Тогда в данных условиях событие А, заключающееся в том, что родился мальчик, и событие В – что родилась девочка, являются противоположными событиями. В= «не А» =Ā.

События называются попарнонесовместными, если любые два из них несовместны. Несколько событий образуют полную группу событий, если они являются попарно несовместными и в результате каждого испытания происходит одно и только одно из них. Пример. При бросании игральной кости могут произойти только следующие события: выпадение грани с цифрой 1, 2, 3, 4, 5 или 6, они образуют полную группу событий.

q События (в опыте) называются равновозможными, если ни одно из них не является объективно более возможным, чем другие. Пример. Выпадение герба (событие А) или решки (событие В) при бросании монеты – равновозможные события (если монета не погнута).

Действия над событиями q Суммой (объединением) двух событий А и В называется событие С=А+В, состоящее в наступлении хотя бы одного из них. q Произведением (пересечением) двух событий А и В называется событие С=А∙В, состоящее в одновременном наступлении (совмещении) событий А и В.

q Разностью двух событий А и В называется событие С=А-В, происходящее тогда и только тогда, когда происходит событие А, но не происходит событие В. q Событие А влечёт событие В (или А является частным случаем В), если из того, что происходит событие А, следует, что происходит событие В. q События А и В называются равносильными (А=В), если событие А влечёт событие В, а событие В влечёт событие А.

Пример Проводится соревнование между учебными группами филологического факультета вуза. Победитель соревнования награждается: денежной премией (событие А), медалью (событие В). Тогда событие А+В состоит в награждении победителя или денежной премией, или медалью, или и тем и другим. Событие А∙В состоит в награждении победителя одновременно и денежной премией, и медалью.

Основные свойства операций над событиями 1. А+В=В+А (коммутативность сложения). 2. (А+В)+С=А+(В+С) (ассоциативность сложения). 3. А·В=В·А (коммутативность умножения). 4. (А·В)·С=А·(В·С) (ассоциативность умножения). 5. (А+В)·С=А·С+В·С или А+В·С=(А+В)·(А+С) (законы дистрибутивности). 6. А+А=А, А·А=А. 7. А+Ω=Ω, А·Ω=А. 8. А+Ø=А, А·Ø=Ø. 9. А+Ā=Ω, А·Ā=Ø. 10. В–А=В·Ā

Вероятность

Пусть проводится опыт с n исходами, которые, в свою, очередь, образуют полную группу равновозможных событий. Данные исходы называют случаями, элементарными событиями, опыт – классическим (схема урн). Случай называется благоприятствующим (благоприятным) событию А, если появление этого случая влечёт за собой наступление события А.

Классический подход к определению вероятности события A где M – число случаев, благоприятствующих наступлению события A, N – общее число случаев.

Пример Дано четыре карточки с буквами У, Р, К, С. Найти вероятность того, что получится слово «КУРС» , если наугад одна за другой выбираются четыре карточки и располагаются в ряд в порядке появления. Решение. Пусть А - событие, состоящее в том, что последовательно вынутые карточки образуют слово «КУРС» . Число случаев, благоприятствующих данному событию, равно 1, т. е. M=1. Между тем заметим, что четырёхбуквенные «слова» отличаются друг от друга лишь порядком расположения букв (УРКС, КРУС и т. д. ) Их число равно числу перестановок без повторений из 4 букв, т. е. число всех случаев равно N=Р 4=4! Тогда искомая вероятность равна Р(А)=1/4!=1/24.

Априорно-частотный подход к определению вероятности события A где m – число испытаний, в которых наступило событие A, n – общее число проведённых испытаний, p* – относительная частота события.

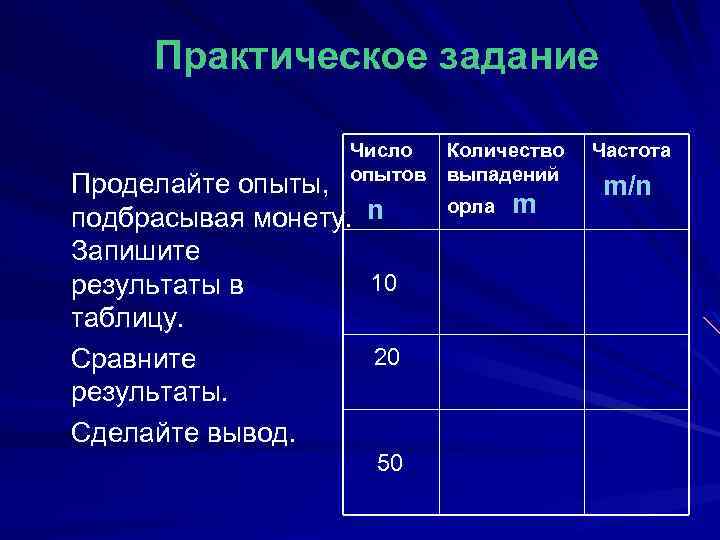Практическое задание Число Количество опытов выпадений Проделайте опыты, подбрасывая монету. Запишите результаты в таблицу. Сравните результаты. Сделайте вывод. n 10 20 50 орла m Частота m/n

Геометрический подход к определению вероятности события A где d - область, благоприятствующая наступлению события A, при этом область d является частью области D. Мерой может быть длина, площадь, объём и т. п.

Пример Поезда в метро идут с интервалом в три минуты. Найти вероятность того, что пассажир будет ждать поезд более двух минут. Решение. Будем считать, что моменты появления пассажира в интервале между поездами равновероятны. Если всё время ожидания принять за интервал длиной три единицы (мера D равна 3 ед. ), то событию А – «время ожидания более двух минут» – будет соответствует одна единица длины (мера d равна 1 ед. ) Следовательно, искомая вероятность равна отношению длин временных интервалов: Р(А)=1/3. d 0 1 D 3

Аксиоматический подход к определению вероятности события A Числовая функция Р(A) называется вероятностью события А, если она удовлетворяет следующим аксиомам. Аксиома 1. Аксиома неотрицательности: вероятность любого события неотрицательна, т. е. Р(A) ≥ 0. Аксиома 2. Аксиома нормированности: вероятность достоверного события равна единице, т. е. Р(Ω)=1. Аксиома 3. Аксиома аддитивности: вероятность суммы двух несовместных событий A и В равна сумме вероятностей этих событий.

Свойства вероятности 1. Вероятность невозможного события равна нулю, т. е. Р(Ø)=0. 2. Вероятность достоверного события равна единице, т. е. Р(Ω)=1.

Свойства вероятности 3. Вероятность случайного события А есть положительное число, заключённое между нулём и единицей, т. е. 0 < Р(А) < 1. 4. Вероятность события, противоположного событию А, равна разности между единицей и вероятностью события Ā.

Основные теоремы вероятности ТЕОРЕМЫ СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ Теорема 1 Для несовместных событий Р(А или В)=Р(А+В)=Р(А)+Р(В) Теорема 2 Для совместных событий Р(А или В)=Р(А+В)= =Р(А)+Р(В)-Р(АВ)

ТЕОРЕМЫ УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ Теорема 3 Теорема 4 Для зависимых событий Для независимых событий Р(А и В)=Р(А∙В)=Р(А)∙Р(В) Р(А и В)=Р(А∙В)= =Р(А)∙Р(В/А), РА(В)=Р(В/А) – условная вероятность события В где

Пример Студент группы Р 23 сдаёт экзамен по дисциплине «Информатика и математика» . В билете два теоретических вопроса (один по информатике, второй по математике). По информатике студент выучил 60 вопросов из 70, по математике – 50 из 60. Найти вероятность того, что студент успешно сдаст теоретическую часть экзамена. Решение. Пусть событие А – студент получит вопрос по информатике, на который знает ответ. Событие В – студенту достанется вопрос по математике, который учил. В свою очередь, событие А∙В – студент успешно сдаст теоретическую часть экзамена. События А и В – независимые, поэтому по теореме 3 имеем: Р(А∙В)=Р(А)∙Р(В)=(60/70)∙(50/60)=0, 71.

Пример Два стрелка стреляют в одну цель, причём вероятность поражения цели первым стрелком равна 0, 8, а вторым – 0, 5. Стрелки стреляют по команде (одновременно) один раз. Найти вероятность того, что цель будет поражена хотя бы одним из стрелков. Решение. Пусть событие А – попадание в цель первым стрелком, событие В – вторым стрелком, тогда А+В – поражение цели хотя бы одним стрелком. В свою очередь, событие А∙В – поражение цели обоими стрелками. События А и В являются совместными и независимыми, поэтому, применяя теоремы 2 и 3, имеем: Р(А+В)=Р(А)+Р(В)-Р(А)∙Р(В)=0, 8+0, 5 -0, 8∙ 0, 5=0, 9.

Список рекомендуемой литературы 1. Воронов М. В. , Мещерякова Г. П. 2. 3. 4. Математика для студентов гуманитарных факультетов. – Ростов-на-Дону, 2002. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М. , 2001. Грес П. В. Математика для гуманитариев. – М. , 2005. Кремер Н. Ш. Теория вероятностей и математическая статистика. – М. , 2006.

Домашнее задание 1. Откройте книгу на любой странице и случайным образом выберите одно существительное. Охарактеризуйте событие (как Ω, Ø, случайное), состоящее: а) в написании выбранного слова есть мягкий знак; б) в написании выбранного слова есть гласная буква; в) в написании выбранного слова нет гласной буквы. 2. Повторите формулы по комбинаторике. 3. Выполните практическое задание.

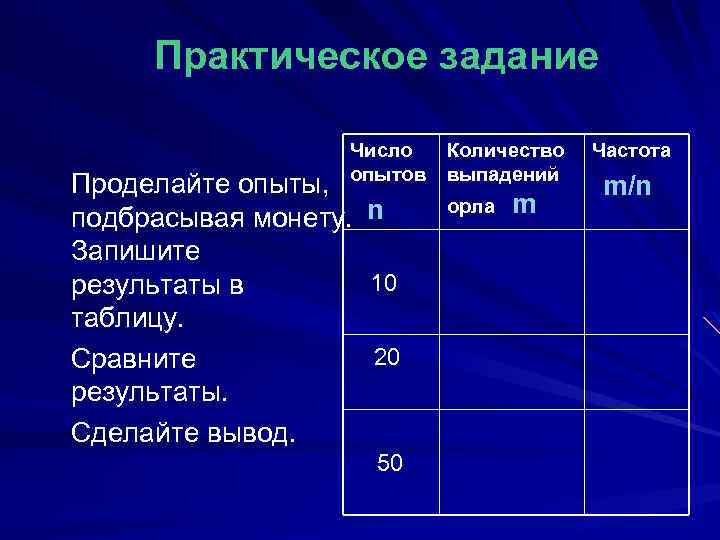Практическое задание Число Количество опытов выпадений Проделайте опыты, подбрасывая монету. Запишите результаты в таблицу. Сравните результаты. Сделайте вывод. n 10 20 50 орла m Частота m/n

Подведение итогов q С какими основными понятиями теории вероятностей вы познакомились? q Какие основные действия можно осуществлять с событиями? q Какие подходы к определению вероятности существуют? q С какими основными теоремами вероятности вы познакомились?

Благодарю за внимание!