Презентация 4.ppt
- Количество слайдов: 27
 Теория вероятностей Лекции по математике
Теория вероятностей Лекции по математике
 Рекомендуемая литература n Кремер Н. Ш. Теория вероятностей и математическая статистика. - М. : Банки и биржи, ЮНИТИ, 2001. n Гмурман В. Е. Теория вероятностей и математическая статистика. - М. : В. Ш. , 2002. n Тимошина И. Р. Электронный конспект лекций по теории вероятностей. ВФ СПб. ГУСЭ, 2007. 2
Рекомендуемая литература n Кремер Н. Ш. Теория вероятностей и математическая статистика. - М. : Банки и биржи, ЮНИТИ, 2001. n Гмурман В. Е. Теория вероятностей и математическая статистика. - М. : В. Ш. , 2002. n Тимошина И. Р. Электронный конспект лекций по теории вероятностей. ВФ СПб. ГУСЭ, 2007. 2
 Содержание n Приближённые формулы теории вероятностей n Наивероятнейшее число появлений события в серии независимых испытаний n Оценка отклонения частоты события от вероятности этого события 3
Содержание n Приближённые формулы теории вероятностей n Наивероятнейшее число появлений события в серии независимых испытаний n Оценка отклонения частоты события от вероятности этого события 3
 Приближённые формулы теории вероятностей n При больших n использование формулы Бернулли затруднительно. n В этих случаях используют либо формулу Лапласа (локальная теорема Лапласа), либо формулу Пуассона, либо интегральную формулу Лапласа. 4
Приближённые формулы теории вероятностей n При больших n использование формулы Бернулли затруднительно. n В этих случаях используют либо формулу Лапласа (локальная теорема Лапласа), либо формулу Пуассона, либо интегральную формулу Лапласа. 4
 Пример n Найти вероятность того, что в серии из 243 испытаний событие наступит 70 раз, если вероятность наступления этого события в одном испытании p=0, 25 n Решение. По формуле Бернулли: Мы столкнулись с ситуацией, что несмотря на наличие точной вычислительной формулы, воспользоваться ею затруднительно!!! n Для решения задач, в которых количество испытаний велико, применяют приближённые формулы. © И. Р. Тимошина «Множества. Числовые функции» 5
Пример n Найти вероятность того, что в серии из 243 испытаний событие наступит 70 раз, если вероятность наступления этого события в одном испытании p=0, 25 n Решение. По формуле Бернулли: Мы столкнулись с ситуацией, что несмотря на наличие точной вычислительной формулы, воспользоваться ею затруднительно!!! n Для решения задач, в которых количество испытаний велико, применяют приближённые формулы. © И. Р. Тимошина «Множества. Числовые функции» 5
 Локальная теорема Лапласа n Если в серии независимых испытаний количество испытаний n велико (npq>20), то можно пользоваться приближённой формулой: 6
Локальная теорема Лапласа n Если в серии независимых испытаний количество испытаний n велико (npq>20), то можно пользоваться приближённой формулой: 6
 Свойства функции f(x) 1. Функция f(x) – чётная, т. е. f(-x)= f(x) 2. . 4. Значения функции f(x) табулированы в диапазоне [0, 5] (таблица) 5. Для |x|≥ 5 можно считать, что f(x)≈0 6. График функции f(x) имеет вид: 7
Свойства функции f(x) 1. Функция f(x) – чётная, т. е. f(-x)= f(x) 2. . 4. Значения функции f(x) табулированы в диапазоне [0, 5] (таблица) 5. Для |x|≥ 5 можно считать, что f(x)≈0 6. График функции f(x) имеет вид: 7
 Формула Лапласа 8
Формула Лапласа 8
 Пример n Найти вероятность того, что в серии из 243 испытаний событие наступит 70 раз, если вероятность наступления этого события в одном испытании p=0, 25 n Решение. Применим для решения формулу Лапласа. n=243 m=70 p=0, 25 q=0, 75 Таблица © И. Р. Тимошина «Множества. Числовые функции» 9
Пример n Найти вероятность того, что в серии из 243 испытаний событие наступит 70 раз, если вероятность наступления этого события в одном испытании p=0, 25 n Решение. Применим для решения формулу Лапласа. n=243 m=70 p=0, 25 q=0, 75 Таблица © И. Р. Тимошина «Множества. Числовые функции» 9
 Формула Пуассона n Если событие А очень маловероятно, т. е. величина p (или q) очень маленькая, то может оказаться, что величина npq мала даже при значительном количестве испытаний n (напомним, что формула Лапласа даёт хорошее приближение, если npq>20). n В этом случае применяют формулу Пуассона: 10
Формула Пуассона n Если событие А очень маловероятно, т. е. величина p (или q) очень маленькая, то может оказаться, что величина npq мала даже при значительном количестве испытаний n (напомним, что формула Лапласа даёт хорошее приближение, если npq>20). n В этом случае применяют формулу Пуассона: 10
 Формула Пуассона n Число называется параметром распределения Пуассона, а сама формула выражает «закон редких, но массовых явлений» . 11
Формула Пуассона n Число называется параметром распределения Пуассона, а сама формула выражает «закон редких, но массовых явлений» . 11
 Пример Завод отправил на базу 5000 проверенных изделий без брака. Вероятность того, что в пути изделие повредится, равно 0, 0002. Найти вероятность того, что на базу прибудут три негодных изделия. © И. Р. Тимошина «Множества. Числовые функции» Решение. По условию n=5000; p=0, 0002; q=0, 9998 Значение npq = 5000∙ 0, 0002∙ 0, 9998≈1<20. Формула Лапласа имеет значительную погрешность! Поэтому применим формулу Пуассона: λ=np=5000∙ 0, 0002=1 12
Пример Завод отправил на базу 5000 проверенных изделий без брака. Вероятность того, что в пути изделие повредится, равно 0, 0002. Найти вероятность того, что на базу прибудут три негодных изделия. © И. Р. Тимошина «Множества. Числовые функции» Решение. По условию n=5000; p=0, 0002; q=0, 9998 Значение npq = 5000∙ 0, 0002∙ 0, 9998≈1<20. Формула Лапласа имеет значительную погрешность! Поэтому применим формулу Пуассона: λ=np=5000∙ 0, 0002=1 12
 Пример n Найти вероятность выпадения от 47 до 57 «орлов» при 100 бросках монеты. n Решение. Вероятность данного события можно вычислить по формулам Бернулли: P 100(47≤ m ≤ 57)=P 100(47)+P 100(48)+…+P 100(57)= =С 10047 p 47 q 53+С 10048 p 48 q 52+…+С 10057 p 57 q 43 Несмотря на наличие точной вычислительной формулы, воспользоваться ею затруднительно!!! © И. Р. Тимошина «Множества. Числовые функции» 13
Пример n Найти вероятность выпадения от 47 до 57 «орлов» при 100 бросках монеты. n Решение. Вероятность данного события можно вычислить по формулам Бернулли: P 100(47≤ m ≤ 57)=P 100(47)+P 100(48)+…+P 100(57)= =С 10047 p 47 q 53+С 10048 p 48 q 52+…+С 10057 p 57 q 43 Несмотря на наличие точной вычислительной формулы, воспользоваться ею затруднительно!!! © И. Р. Тимошина «Множества. Числовые функции» 13
 Интегральная теорема Лапласа n Вероятность того, что в серии независимых испытаний событие произойдёт не менее k 1 раз и не более k 2 раз, т. е. Pn (k 1≤m≤k 2) вычисляется по формуле: 14
Интегральная теорема Лапласа n Вероятность того, что в серии независимых испытаний событие произойдёт не менее k 1 раз и не более k 2 раз, т. е. Pn (k 1≤m≤k 2) вычисляется по формуле: 14
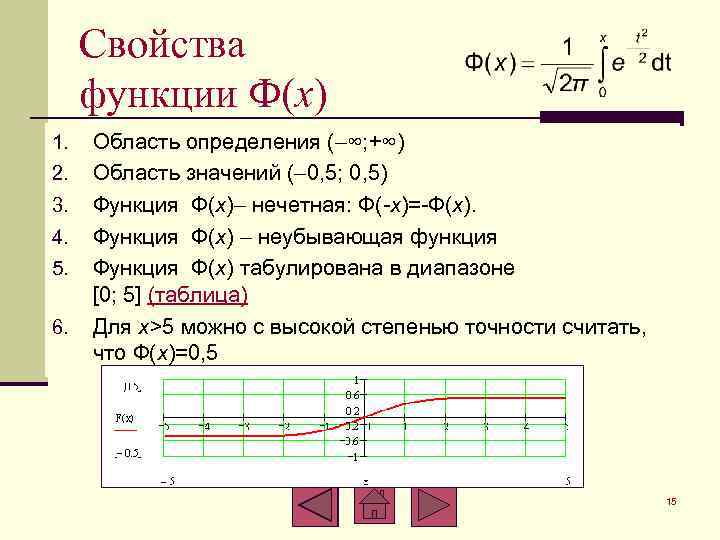 Свойства функции Ф(x) 1. 2. 3. 4. 5. 6. Область определения ( ∞; +∞) Область значений ( 0, 5; 0, 5) Функция Ф(x) нечетная: Ф(-x)=-Ф(x). Функция Ф(x) неубывающая функция Ф(x) табулирована в диапазоне [0; 5] (таблица) Для x>5 можно с высокой степенью точности считать, что Ф(x)=0, 5 15
Свойства функции Ф(x) 1. 2. 3. 4. 5. 6. Область определения ( ∞; +∞) Область значений ( 0, 5; 0, 5) Функция Ф(x) нечетная: Ф(-x)=-Ф(x). Функция Ф(x) неубывающая функция Ф(x) табулирована в диапазоне [0; 5] (таблица) Для x>5 можно с высокой степенью точности считать, что Ф(x)=0, 5 15
 Пример n Найти вероятность выпадения от 47 до 57 «орлов» при 100 бросках монеты. n Решение. Применим интегральную теорему Лапласа: n=100; k 1=47; k 2=57; p=0, 5; q=0, 5; Ответ. Р 100(47
Пример n Найти вероятность выпадения от 47 до 57 «орлов» при 100 бросках монеты. n Решение. Применим интегральную теорему Лапласа: n=100; k 1=47; k 2=57; p=0, 5; q=0, 5; Ответ. Р 100(47
 Наивероятнейшее число появлений события Пример. Вероятность изготовления на автоматическом станке бракованной детали равна 0, 2. Найти вероятности возможного числа появлений бракованных деталей среди 5 отобранных. © И. Р. Тимошина «Множества. Числовые функции» Решение. 1. p=0, 2; q=0, 8 2. Искомые вероятности находим по формуле Бернулли: 17
Наивероятнейшее число появлений события Пример. Вероятность изготовления на автоматическом станке бракованной детали равна 0, 2. Найти вероятности возможного числа появлений бракованных деталей среди 5 отобранных. © И. Р. Тимошина «Множества. Числовые функции» Решение. 1. p=0, 2; q=0, 8 2. Искомые вероятности находим по формуле Бернулли: 17
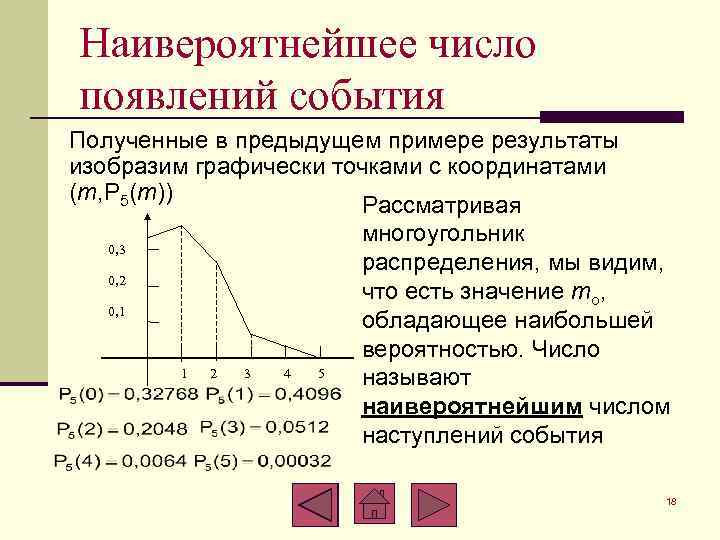 Наивероятнейшее число появлений события Полученные в предыдущем примере результаты изобразим графически точками с координатами (m, P 5(m)) Рассматривая многоугольник 0, 3 распределения, мы видим, 0, 2 что есть значение mо, 0, 1 обладающее наибольшей вероятностью. Число 1 2 3 4 5 называют наивероятнейшим числом наступлений события 18
Наивероятнейшее число появлений события Полученные в предыдущем примере результаты изобразим графически точками с координатами (m, P 5(m)) Рассматривая многоугольник 0, 3 распределения, мы видим, 0, 2 что есть значение mо, 0, 1 обладающее наибольшей вероятностью. Число 1 2 3 4 5 называют наивероятнейшим числом наступлений события 18
 Наивероятнейшее число появлений события © И. Р. Тимошина «Множества. Числовые функции» 19
Наивероятнейшее число появлений события © И. Р. Тимошина «Множества. Числовые функции» 19
 Наивероятнейшее число появлений события n Для нахождения значения mо в общем случае запишем систему неравенств: n Решим первое неравенство, воспользовавшись формулой Бернулли : 20
Наивероятнейшее число появлений события n Для нахождения значения mо в общем случае запишем систему неравенств: n Решим первое неравенство, воспользовавшись формулой Бернулли : 20
 Наивероятнейшее число появлений события Проведя необходимые сокращения, получим: 21
Наивероятнейшее число появлений события Проведя необходимые сокращения, получим: 21
 Наивероятнейшее число появлений события Решая второе неравенство, получим: Объединяя полученные решения, придём к двойному неравенству: 22
Наивероятнейшее число появлений события Решая второе неравенство, получим: Объединяя полученные решения, придём к двойному неравенству: 22
 Пример n Пример. Вероятность изготовления на автоматическом станке бракованной детали равна 0, 2. Найти наивероятнейшее число появления бракованных деталей из пяти отобранных. © И. Р. Тимошина «Множества. Числовые функции» n Решение. Применим формулу: 5∙ 0, 2 0, 8≤mo≤ 5∙ 0, 2+0, 2 ≤ mo ≤ 1, 2 Ответ. mo=1 23
Пример n Пример. Вероятность изготовления на автоматическом станке бракованной детали равна 0, 2. Найти наивероятнейшее число появления бракованных деталей из пяти отобранных. © И. Р. Тимошина «Множества. Числовые функции» n Решение. Применим формулу: 5∙ 0, 2 0, 8≤mo≤ 5∙ 0, 2+0, 2 ≤ mo ≤ 1, 2 Ответ. mo=1 23
 Оценка отклонения частоты события от вероятности этого события n Пусть проводится серия из независимых испытаний. Вероятность появления события А в каждом из этих испытаний равна p. n Тогда частота (относительная частота) этого события равна m/ n. n Очевидно, что частота события является случайной величиной. Она может оказаться как больше вероятности события p, так и меньше этой вероятности. 24
Оценка отклонения частоты события от вероятности этого события n Пусть проводится серия из независимых испытаний. Вероятность появления события А в каждом из этих испытаний равна p. n Тогда частота (относительная частота) этого события равна m/ n. n Очевидно, что частота события является случайной величиной. Она может оказаться как больше вероятности события p, так и меньше этой вероятности. 24
 Оценка отклонения частоты события от вероятности этого события n Рассмотрим модуль разности этих величин: Выберем некоторое число ε>0. n Задача. Оценить вероятность того, что отклонение относительной частоты от вероятности p по модулю не превосходит числа ε, т. е 25
Оценка отклонения частоты события от вероятности этого события n Рассмотрим модуль разности этих величин: Выберем некоторое число ε>0. n Задача. Оценить вероятность того, что отклонение относительной частоты от вероятности p по модулю не превосходит числа ε, т. е 25
 Решение В соответствии с приближённой формулой Лапласа: = © И. Р. Тимошина «Множества. Числовые функции» 26
Решение В соответствии с приближённой формулой Лапласа: = © И. Р. Тимошина «Множества. Числовые функции» 26
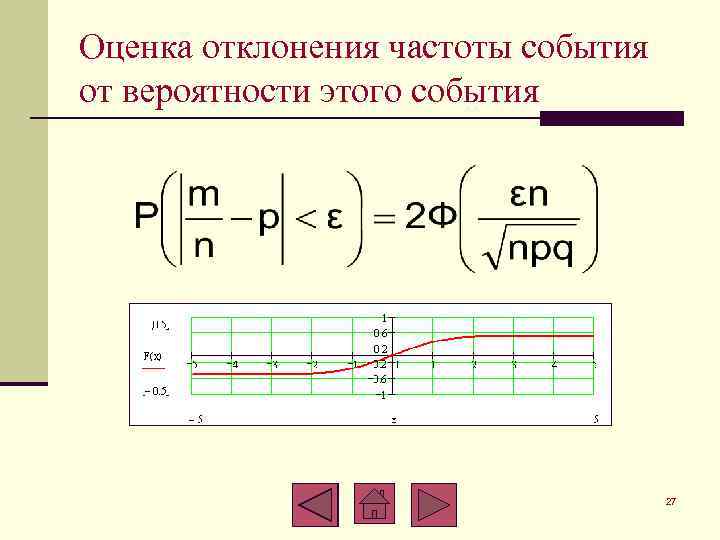 Оценка отклонения частоты события от вероятности этого события 27
Оценка отклонения частоты события от вероятности этого события 27


