ТЕОРИЯ ВЕРОЯТНОСТЕЙ 3 Определение случайной величины Дискретные и

ТЕОРИЯ ВЕРОЯТНОСТЕЙ 3. Определение случайной величины. Дискретные и непрерывные случайные величины. Функция распределения и ее свойства, плотность вероятностей непрерывной случайной величины. Биномиальное распределение. Распределение Пуассона.

Случайная величина Со многими испытаниями могут быть связаны не только какие-то случайные события, но также и случайные числа. Это может быть число очков на выпавших кубиках, число бракованных деталей в наугад выбранной партии, выигрыш (денежный) в некой игре и т. п. В связи с этим в теории вероятностей вводится понятие случайной величины. Случайной величиной называется величина Х, которая в результате испытания может принимать единственное значение х, из заданных, заранее неизвестное.

Дискретная случайная величина Пусть {х1, х2, …, хn} – конечный набор чисел (чаще всего в порядке возрастания). Дискретной случайной величиной (сокращенно, ДСВ) называется величина Х, которая в результате испытания может принимать одно из значений хi, заранее неизвестное.

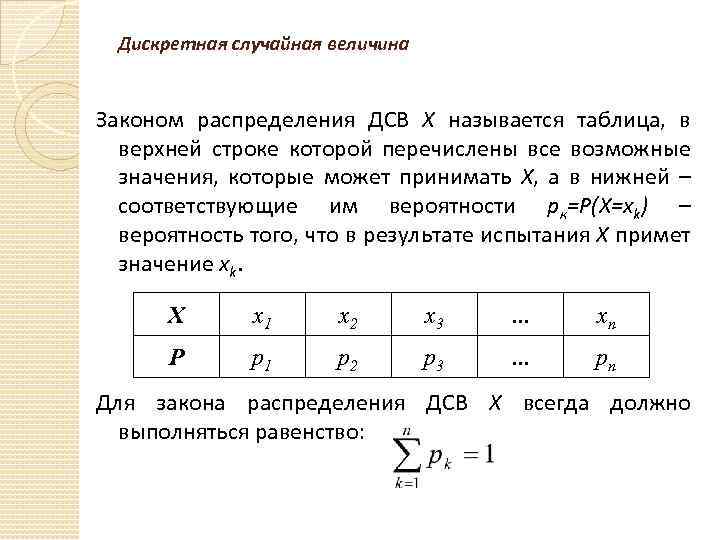Дискретная случайная величина Законом распределения ДСВ Х называется таблица, в верхней строке которой перечислены все возможные значения, которые может принимать Х, а в нижней – соответствующие им вероятности рк=Р(Х=хk) – вероятность того, что в результате испытания Х примет значение хk. Х х1 х2 х3 … хn Р р1 р2 р3 … рn Для закона распределения ДСВ Х всегда должно выполняться равенство:

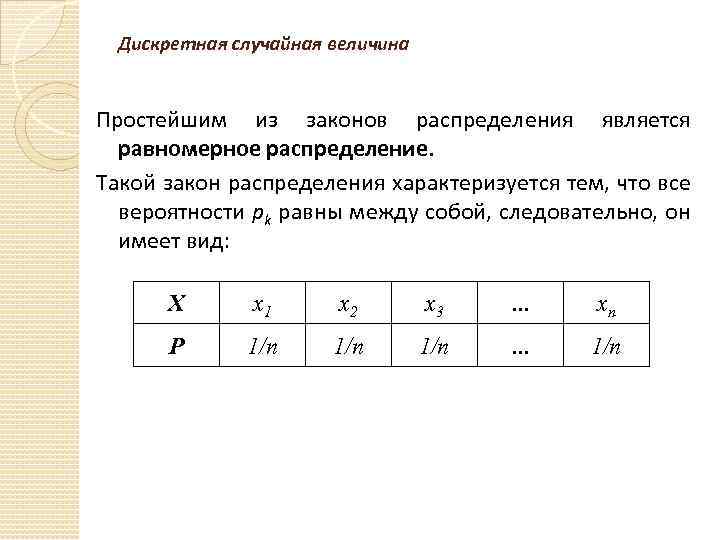Дискретная случайная величина Простейшим из законов распределения является равномерное распределение. Такой закон распределения характеризуется тем, что все вероятности рk равны между собой, следовательно, он имеет вид: Х х1 х2 х3 … хn Р 1/n 1/n … 1/n

ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ (СХЕМА БЕРНУЛЛИ)

Последовательность независимых испытаний (схема Бернулли) Рассмотрим некоторое испытание и связанное с ним случайное событие А. Пусть это испытание повторяется многократно при неизменных условиях. В таком случае говорят, что производится последовательность независимых испытаний (иногда это называется схемой Бернулли). римером является игра двух сторон на определенных условиях (бросание монеты или кубика, шахматы, карточные игры, лотереи, тотализаторы и т. п. ), событие А – это выигрыш одной из сторон в данной игре. В схеме Бернулли принято событие А называть "успехом", а противоположное ему событие А – "неудачей".

Последовательность независимых испытаний (схема Бернулли) Предположим, что производится серия из n независимых испытаний с двумя исходами ("успех" или "неудача") в каждом испытании; р – вероятность "успеха"; q=1–р – вероятность "неудачи" (обычно р и q либо заданы, либо легко вычисляются). Обозначим через k число успехов в этой серии, которое может принимать любые значения от 0 до n. Событие Mk, состоящее в том, что число успехов в нашей серии испытаний окажется равным именно числу k, является случайным. Его вероятность Р(Mk) (Рn(k)) может быть найдена по формуле Бернулли:

Пример Задача 17. Монету бросают 10 раз. Найти вероятность того, что число выпавших "орлов" и "решек" будут одинаковым.

Пример (задача 17)

Пример Задача 18. Кубик бросают 4 раза. Какова вероятность того, что не меньше двух раз выпадет цифра, большая четырех?

Пример (задача 18) Решение: Будем понимать под успехом выпадение на кубике при одном бросании цифры, большей четырех (т. е. 5 или 6). Очевидно, вероятность успеха р=2/6=1/3; (q=2/3). Общее число испытаний n=4. Число успехов k должно быть равно 2, 3 или 4. Поэтому, применяя три раза формулу Бернулли, получим искомую вероятность

Пример Задача 19. Вероятность попадания в цель при одном выстреле равна р=1/2. Известно, что для полного поражения цели требуется не менее трех попаданий. Какое минимальное количество выстрелов нужно произвести, чтобы с вероятностью не менее, чем 0, 9, можно было утверждать, что цель поражена.

Пример (задача 19) Решение: Предположим, что по цели произведено n выстрелов. Тогда вероятность поражения цели будет равна: Минимальное число неравенством: выстрелов или определяется

Пример (продолжение задача 19) Решение: Отсюда по формуле Бернулли: Это неравенство будет выполняться, начиная с n=9. Таким образом, минимальное число выстрелов для поражения цели с вероятностью 0, 9 будет равно 9.

Последовательность независимых испытаний (схема Бернулли) Из рассмотренных примеров видно, что формулой Бернулли нетрудно пользоваться, если число испытаний n невелико. На практике же встречаются серии из нескольких десятков, сотен и даже тысяч испытаний. В таких случаях формула Бернулли практически непригодна.

БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Биномиальное распределение Рассмотрим схему Бернулли (n – число всех испытаний; р – вероятность успеха в одном испытании; q=1–р – вероятность неудачи). Пусть случайная величина Х – это число успехов во всей серии. Для любого 0 k n вероятность того, что Х в результате серии испытаний примет значение k вычисляется по формуле Бернулли: Полученный таким образом называется биномиальным: закон распределения Х 0 1 … k … n Р Pn(0) Pn(1) … Pn(k) … Pn(n)

Распределение Пуассона Закон распределения Пуассона имеет вид: Распределение Пуассона является предельным случаем биномиального распределения, когда n – велико, р – мало, а =n p.

Распределение Пуассона Пусть производится n независимых испытаний, в которых появление события А имеет вероятность р и число испытаний n достаточно велико (n > 50), а вероятность появления события А в каждом испытании мала (p 0, 1). Сделаем важное допущение – произведение n∙р сохраняет постоянное значение: =n p. T. е. среднее число появления события в различных сериях из испытаний остается неизменным. Используя формулу Бернулли получаем формулу распределения Пуассона:

Геометрическое распределение Предположим, что вероятность попадания в цель при одном выстреле равна р, q=1–р – вероятность промаха. Испытание заключается в том, что стреляют в цель до первого попадания и на этом стрельба заканчивается. Число произведенных выстрелов Х является случайной величиной, которая может принимать любые целые значения k 1. Найдем закон распределения Х. Для этого рассмотрим следующие случайные события: А 1 – при первом выстреле был промах; А 2 – при втором выстреле был промах; … и т. д.

Геометрическое распределение События А 1, А 2… – попарно независимы. Поэтому по формуле умножения вероятностей получим: Таким образом, получаем закон распределения этой случайной величины, который принято называть геометрическим: Х 0 1 3 … k Р P qp q 2 p … qk-1 p

Непрерывные случайные величины Существуют случайные величины множество значений которой, может быть произвольным: множество всех действительных чисел, полупрямая [а; + ), отрезок [a; b] и т. п. Такие случайные величины, в отличие о дискретных, не могут быть заданы законом распределения. Для любой случайной величины X можно вести понятие функции распределения F(х) в точке x определяется как вероятность того, что в результате испытания случайная величина Х примет значение, меньшее, чем x :

Пример Задача 20. Пусть Х – ДСВ с заданным законом распределения. Найти функцию распределения.

Пример (задача 20) Решение: Разобьем всю прямую на четыре части точками х1=1, х2=2, х3=3. Рассмотрим четыре случая: 1. если х 1, то событие {Х

Пример (продолжение, задача 20) Решение: 4. если x 3, то событие {X

Пример Задача 21. Рассмотрим испытание, состоящее в том, что в заданном круге радиуса R=1 наугад отмечается точка М. Пусть случайная величина Х – это расстояние от точки М до центра круга.

Пример (задача 21) Решение: Рассмотрим три случая: 1. если x 0, то событие {X1, то событие {X

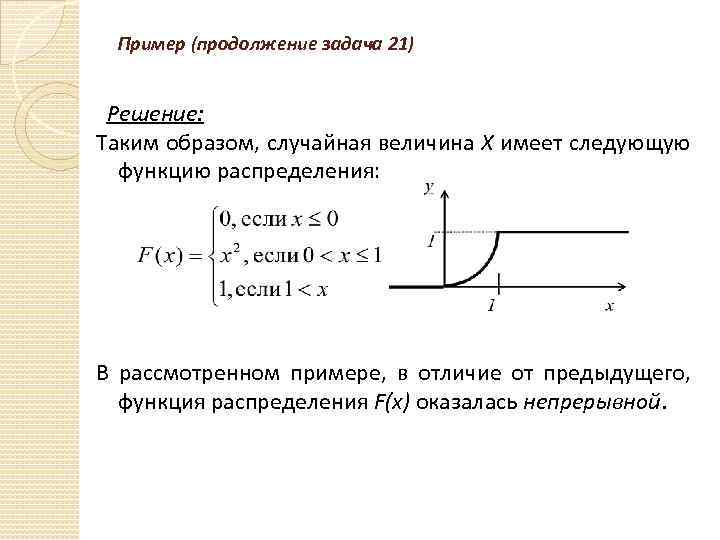Пример (продолжение задача 21) Решение: Таким образом, случайная величина Х имеет следующую функцию распределения: В рассмотренном примере, в отличие от предыдущего, функция распределения F(x) оказалась непрерывной.

Непрерывные случайные величины Другим, важным понятием, связанным с ДСВ Х, является понятие плотности распределения: она обозначается через f(x) и определяется как производная от функции распределения, т. е. Например, в рассмотренной ранее задаче (21) плотность распределения f(x) имеет вид.

Непрерывные случайные величины В некоторых задачах ДСВ Х задается своей плотностью распределения f(x). В таком случае функция распределения F(x) может быть найдена по формуле: Отметим характерные свойства плотности распределения: 1. f(x)≥ 0 для любого x; 2.

Геометрическое распределение Распространенной является задача нахождения вероятности попадания ДСВ Х в заданный интервал (a, b). Эту вероятность можно найти по одной из следующих формул:

Геометрическое распределение Из геометрического смысла определенного интеграла, при a=x и b=x+ x получаем приближенную формулу: Эта формула выражает вероятностный смысл плотности распределения: если всю числовую прямую разбить на достаточно маленькие интервалы одинаковой длины х, то вероятность попадания Х в каждый из этих интервалов пропорциональна значению f(x) на этом интервале.