09.09.2011 - АК1,2,4-91.ppt
- Количество слайдов: 55

Теория управления движением. Спецглавы. (Управление ориентацией и стабилизация КА и ЛА) Симоньянц Р. П. , 9 семестр, 2011. Раздел 1. Летательный аппарат как объект управления ориентацией 1. 1. Геометрия масс ЛА Положение центра масс Тензор инерции (1. 1. 1) Осевые моменты инерции (1. 1. 2) Произведения инерции (1. 1. 3) 1

1. 2. Главные центральные моменты инерции Частный случай: Угловое положение главных центральных осей относительно связанных. Частный случай: 2

1. 3. Ориентация связанных осей 0 xyz относительно опорных 0 x 0 y 0 z 0 1. 3. 1. Направляющие косинусы ракетной системы конечных поворотов Ракетная система поворотов 3
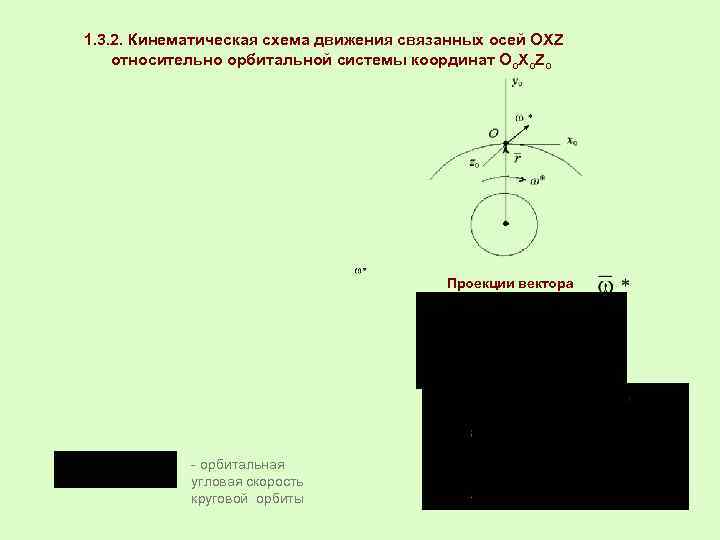
1. 3. 2. Кинематическая схема движения связанных осей ОXZ относительно орбитальной системы координат Оо. Xо. Zо Проекции вектора - орбитальная угловая скорость круговой орбиты 4

1. 4. Кинематические уравнения движения связанных осей относительно орбитальных Из (1. 4. 1) получаем значения производных углов по времени Выражения (1. 4. 2) позволяют выполнить интегрирование уравнений движения 5
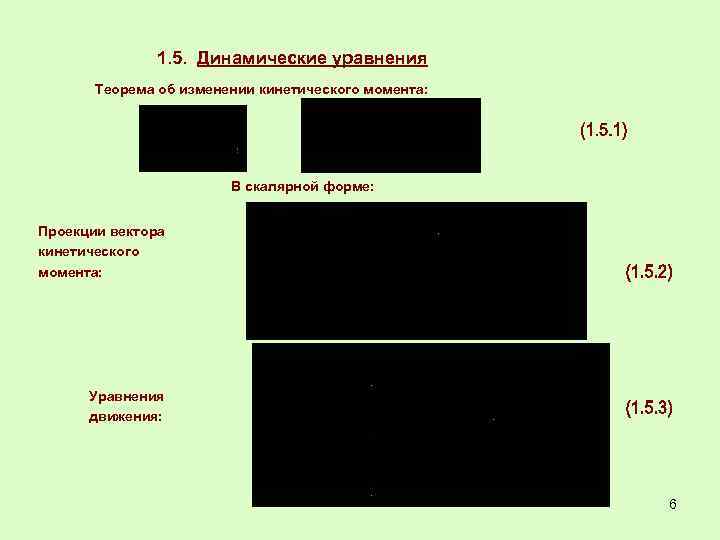
1. 5. Динамические уравнения Теорема об изменении кинетического момента: В скалярной форме: Проекции вектора кинетического момента: Уравнения движения: 6

Уравнения движения в развёрнутом виде: 7

1. 6. Возмущающие моменты 1. 6. 1. Внутренние моменты - Кинетический момент вращающихся на борту масс, - момент электропривода, - Вентиляционный момент, - гироскопические моменты. 1. 62. Моменты реактивных сил - тяга реактивного двигателя ОДУ, - эксцентриситет вектора тяги 8
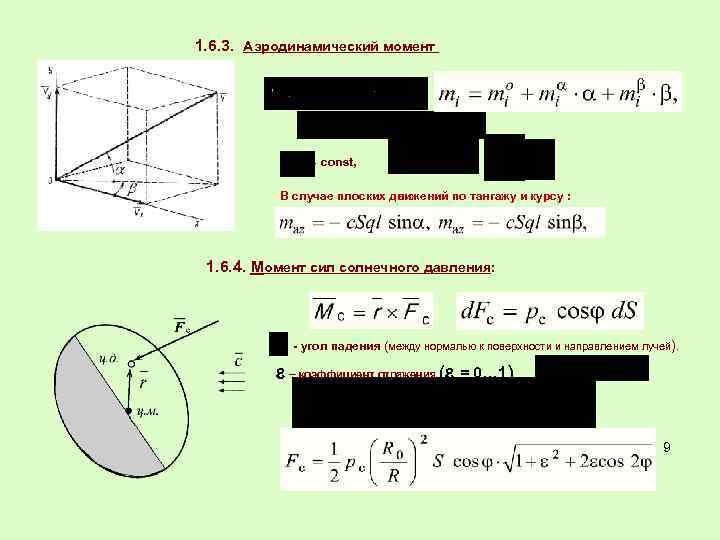
1. 6. 3. Аэродинамический момент – const, В случае плоских движений по тангажу и курсу : 1. 6. 4. Момент сил солнечного давления: - угол падения (между нормалью к поверхности и направлением лучей). – коэффициент отражения ( = 0… 1) 9

1. 6. 5. Момент от взаимодействия с магнитным полем планеты: – индукция магнитного поля Земли; – магнитный момент КЛА; – постоянный магнитный момент; – наведенный магнитный момент - Дипольная модель магнитного поля Земли: - Модуль вектора В: 10
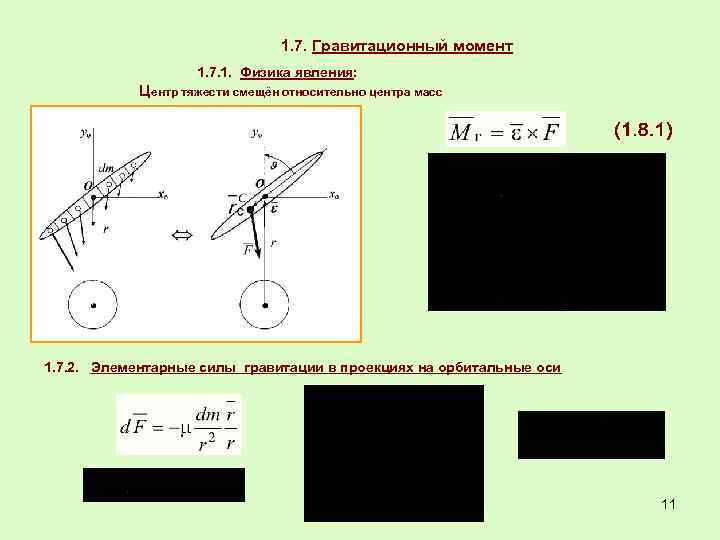
1. 7. Гравитационный момент 1. 7. 1. Физика явления: Центр тяжести смещён относительно центра масс 1. 7. 2. Элементарные силы гравитации в проекциях на орбитальные оси 11
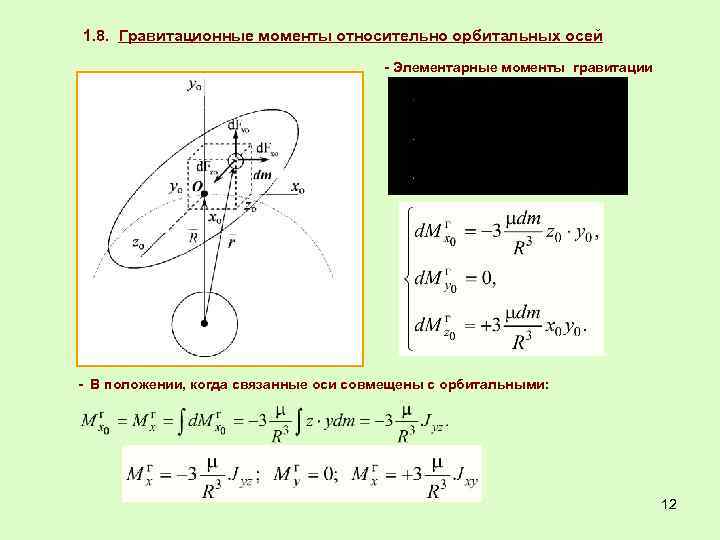
1. 8. Гравитационные моменты относительно орбитальных осей - Элементарные моменты гравитации - В положении, когда связанные оси совмещены с орбитальными: 12

1. 8. 2. Гравитационные моменты относительно связанных осей - Пример для проверки: идеальная стабилизация (связанные оси совмещены с орбитальными осями): 13

1. 8. 2. Гравитационные моменты в плоском движении по тангажу при произвольном тензоре инерции 1. 8. 3. Гравитационные моменты в плоском движении по курсу при произвольном тензоре инерции 1. 8. 4. Гравитационные моменты в плоском движении по крену при произвольном тензоре инерции 14

1. 8. 5. Гравитационные моменты в плоских движениях при диагональном тензоре инерции: 15

1. 9. Гироскопические моменты корпуса при неподвижном положении связанных осей относительно орбитальной системы координат 1. 9. 1. Общий случай ориентации при недиагональном тензоре инерции 1. 9. 2. Связанные оси повёрнуты в плоскости тангажа: 1. 9. 3. . Связанные оси повёрнуты в плоскости курса: 16

1. 9. 2. . Связанные оси повёрнуты в плоскости крена: 1. 9. 2. Гироскопические моменты при плоских отклонениях и диагональном тензоре инерции: 1. 9. 2. Влияние гироскопических моментов орбитального движения - В плоскости тангажа: отсутствует - В плоскостях крена и курса: стабилизирующий эффект, если момент инерции по тангажу максимальный; 17

1. 9. Движение в плоскости тангажа под действием гравитационного момента 1. 9. 1. Случай невозмущённого плоского движения при диагональном тензоре инерции 18
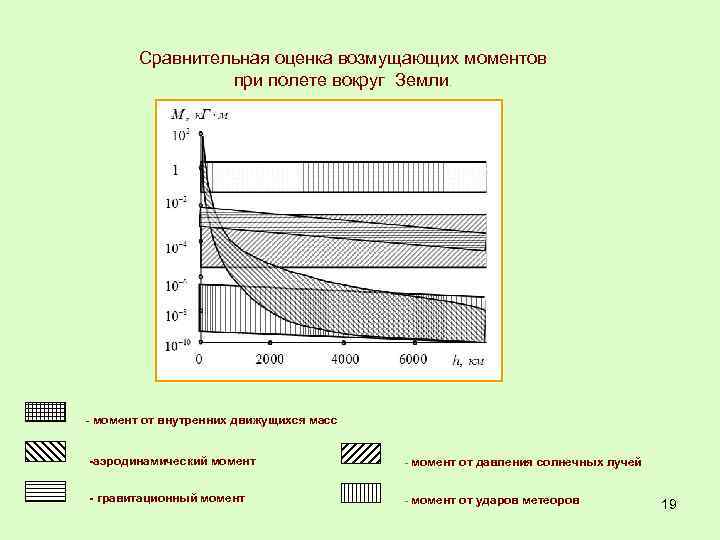
Cравнительная оценка возмущающих моментов при полете вокруг Земли. - момент от внутренних движущихся масс -аэродинамический момент - момент от давления солнечных лучей - гравитационный момент - момент от ударов метеоров 19

Уравнения плоских управляемых движений При условии: 20
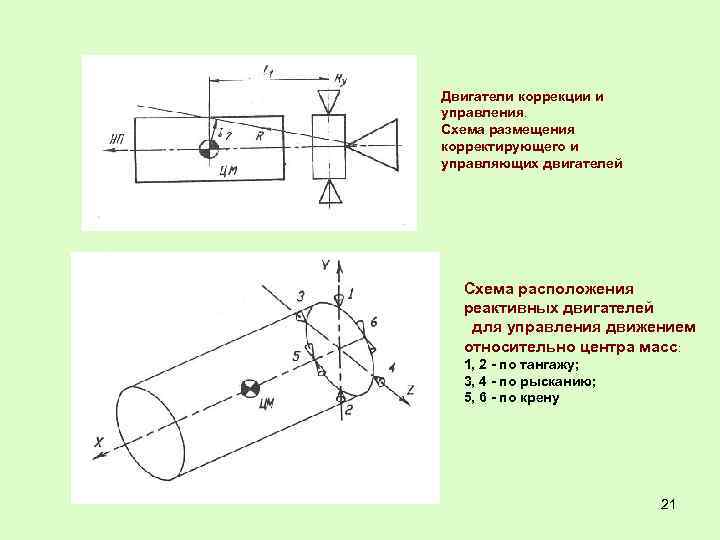
Двигатели коррекции и управления. Схема размещения корректирующего и управляющих двигателей Схема расположения реактивных двигателей для управления движением относительно центра масс: 1, 2 - по тангажу; 3, 4 - по рысканию; 5, 6 - по крену 21
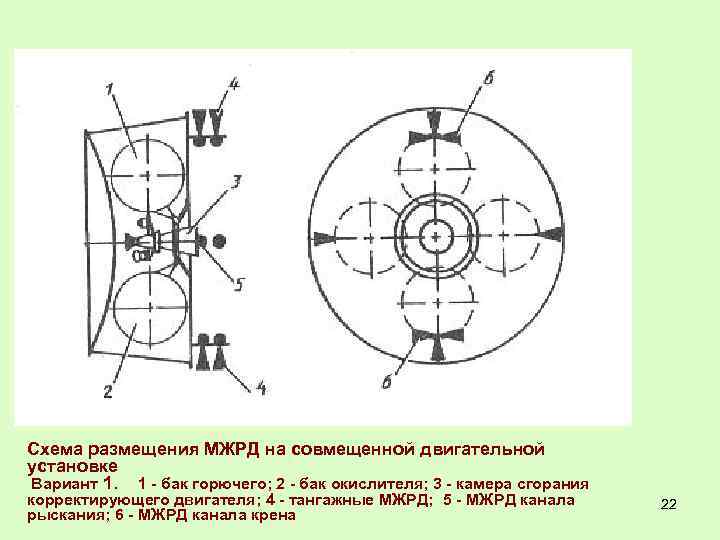
Схема размещения МЖРД на совмещенной двигательной установке Вариант 1. 1 - бак горючего; 2 - бак окислителя; 3 - камера сгорания корректирующего двигателя; 4 - тангажные МЖРД; 5 - МЖРД канала рыскания; 6 - МЖРД канала крена 22
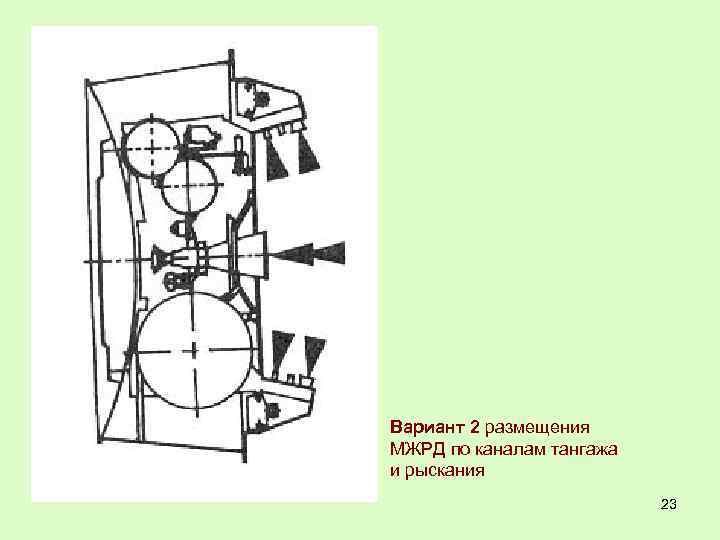
Вариант 2 размещения МЖРД по каналам тангажа и рыскания 23

Математические модели нелинейных элементов 24

1 -1 25

Линии переключения ( границы листов ) фазовой поверхности 26
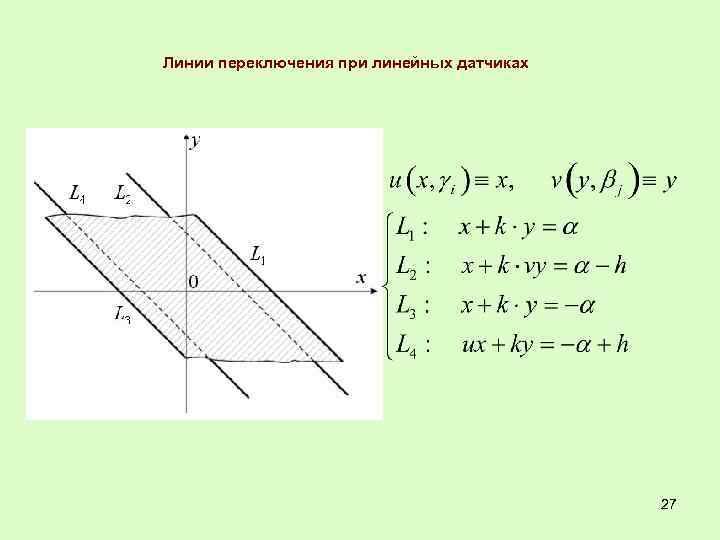
Линии переключения при линейных датчиках 27

Линии переключения при нелинейном датчике скорости 28
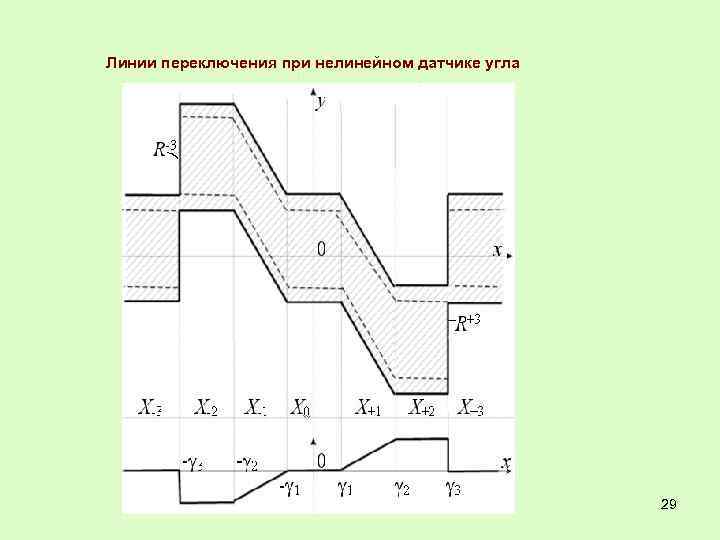
Линии переключения при нелинейном датчике угла 29

Структура разбиения фазовой поверхности в общем случае 30

Бифуркации структуры фазовой поверхности Параметры нелинейностей датчиков = 2 - 1 , = k · ( 2 - 1 ) Параметр структуры S = n 1 + 2 n 1 - число наклонных участков, n 2 - число вертикальных участков S 24 = - , > 2 S 57 = - , < 2 S 47 = > /2 S 25 = < /2 S 34 = > S 67 = < S 36 = > S 79 = - , < 2 S 89 = < /2 S 68 = - , > 2 31

Полибифуркации структур S 2457 : при = = /2; S 3467 : при = = ; S 6789: при = = /2. 32

Фазовые траектории при постоянном возмущении ( g = const) Общий вид 33
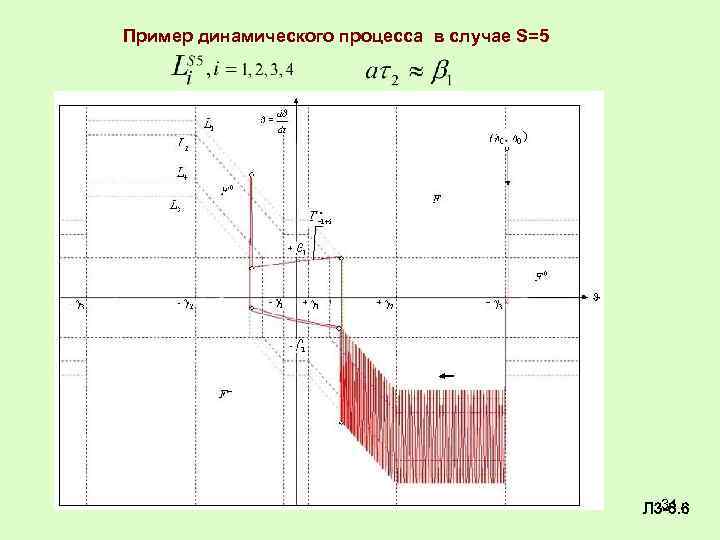
Пример динамического процесса в случае S=5 34
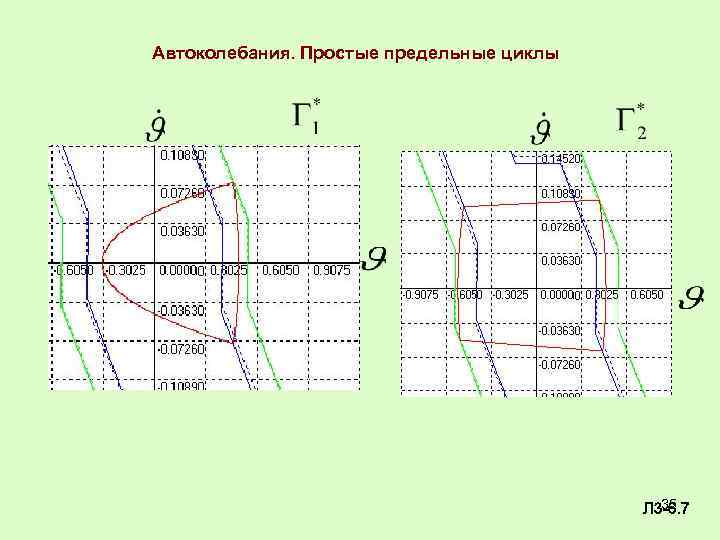
Автоколебания. Простые предельные циклы 35
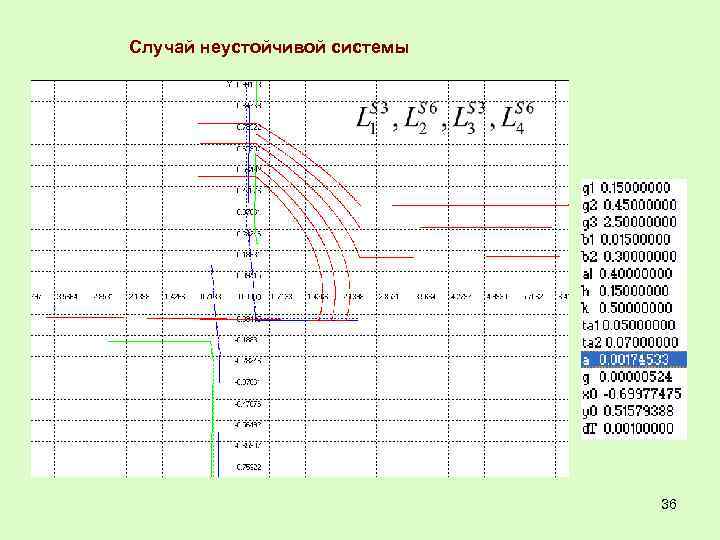
Случай неустойчивой системы 36
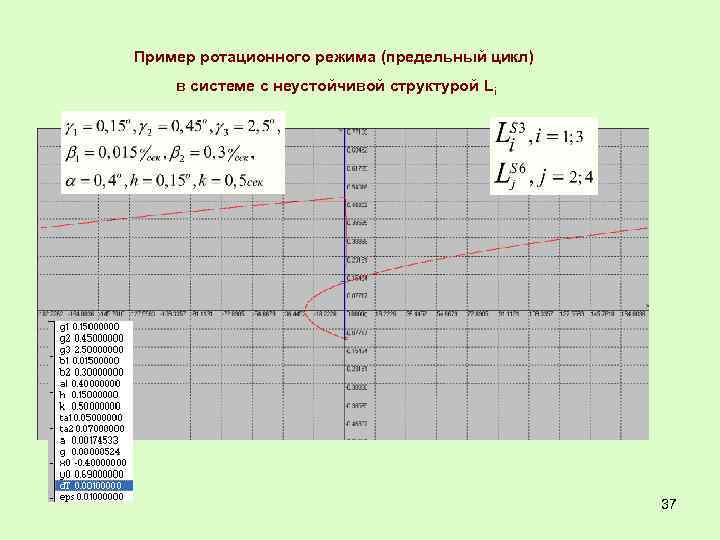
Пример ротационного режима (предельный цикл) в системе с неустойчивой структурой Li 37

Пример локально устойчивой системы 38
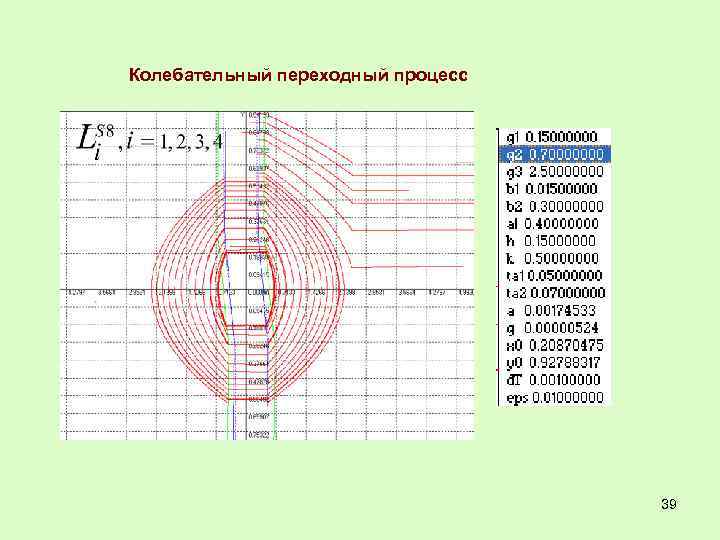
Колебательный переходный процесс 39
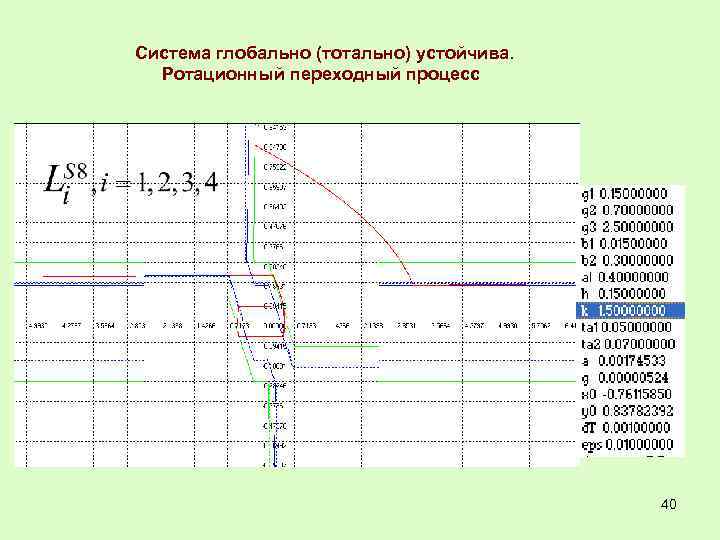
Система глобально (тотально) устойчива. Ротационный переходный процесс 40
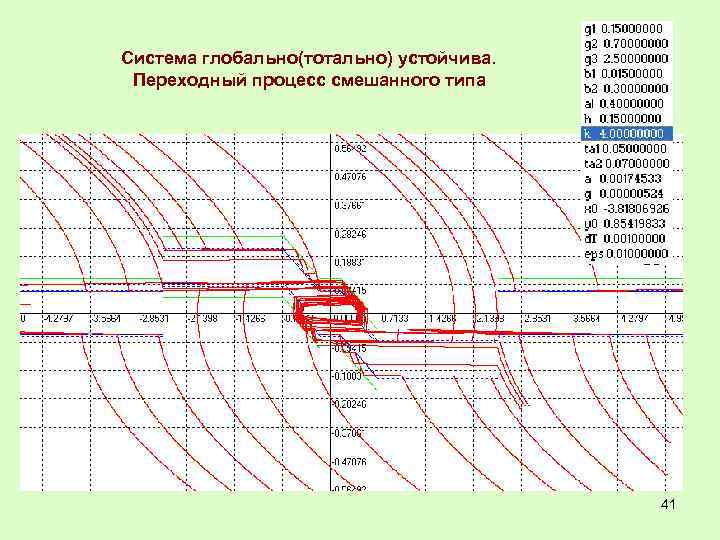
Система глобально(тотально) устойчива. Переходный процесс смешанного типа 41
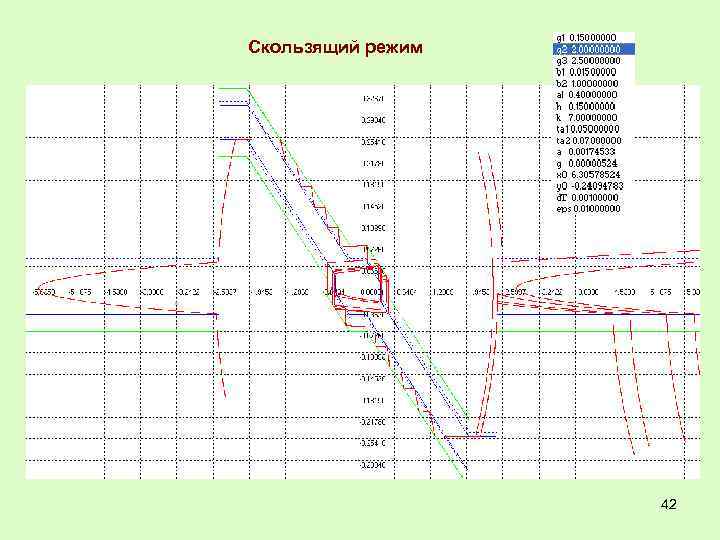
Скользящий режим 42
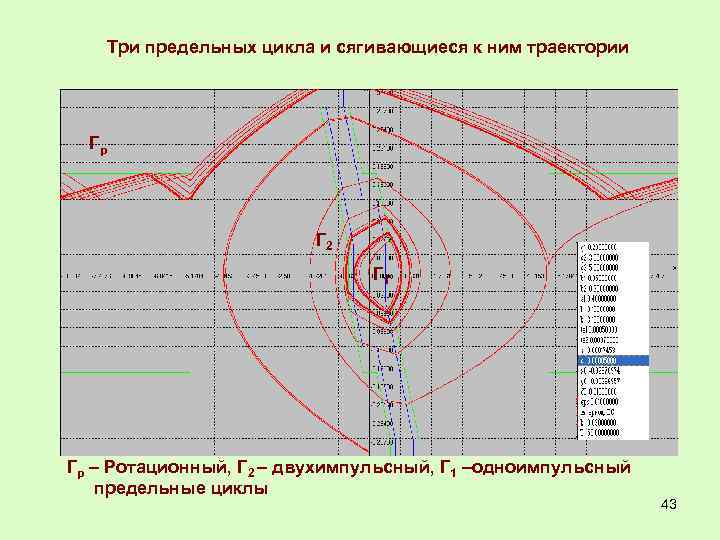
Три предельных цикла и сягивающиеся к ним траектории Гр Г 2 Г 1 Гр – Ротационный, Г 2 – двухимпульсный, Г 1 –одноимпульсный предельные циклы 43
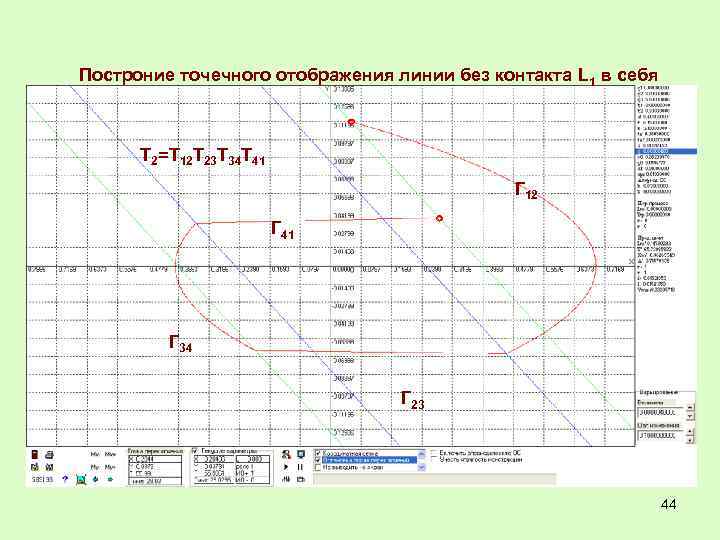
Построние точечного отображения линии без контакта L 1 в себя Т 2=Т 12 Т 23 Т 34 Т 41 Г 12 Г 41 Г 34 Г 23 44
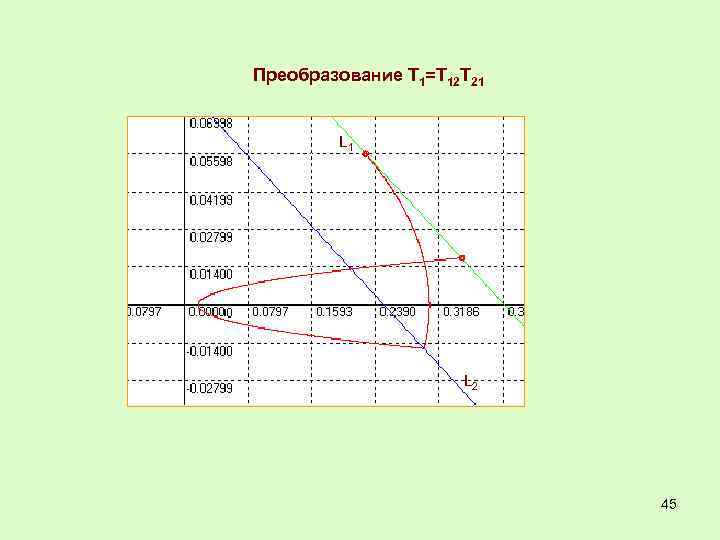
Преобразование Т 1=Т 12 Т 21 L 2 45
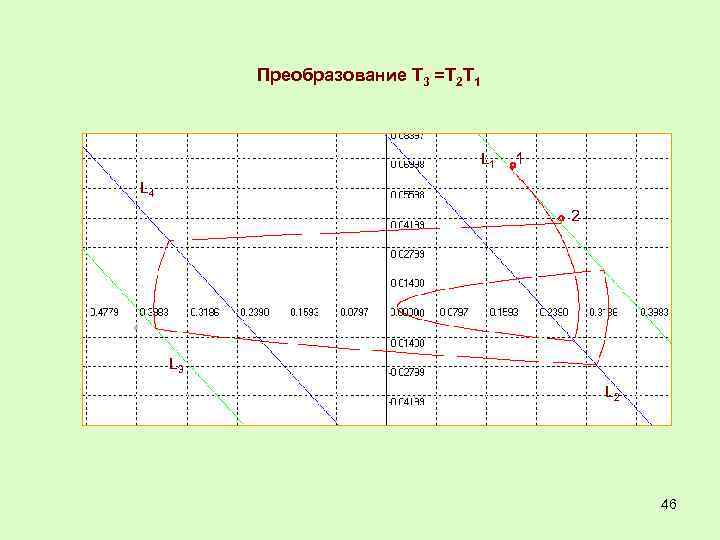
Преобразование Т 3 =Т 2 Т 1 L 1 1 L 4 2 L 3 L 2 46
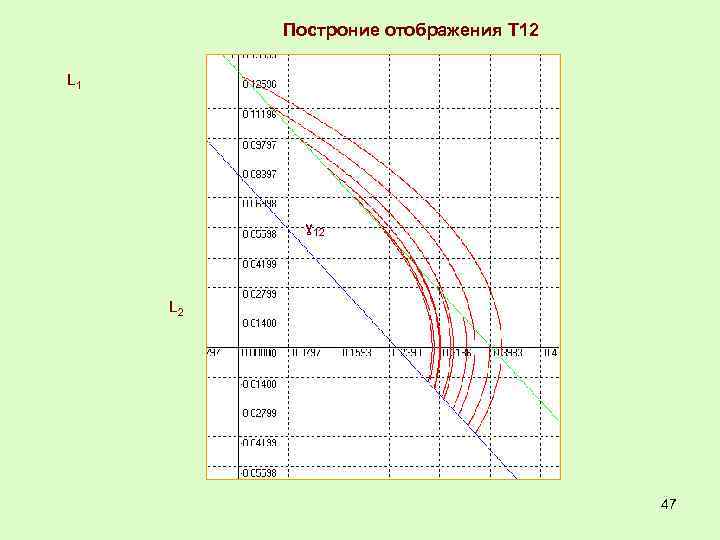
Построние отображения Т 12 L 1 ɣ 12 L 2 47
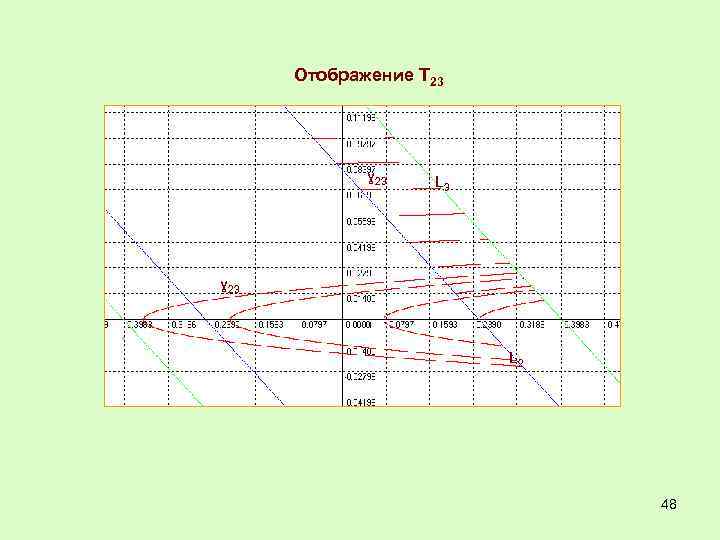
Отображение Т 23 ɣ 23 L 2 48
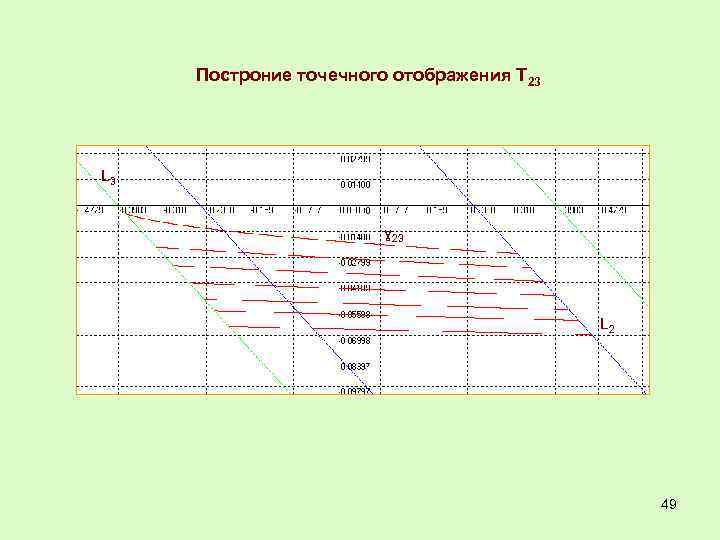
Построние точечного отображения Т 23 L 3 ɣ 23 L 2 49
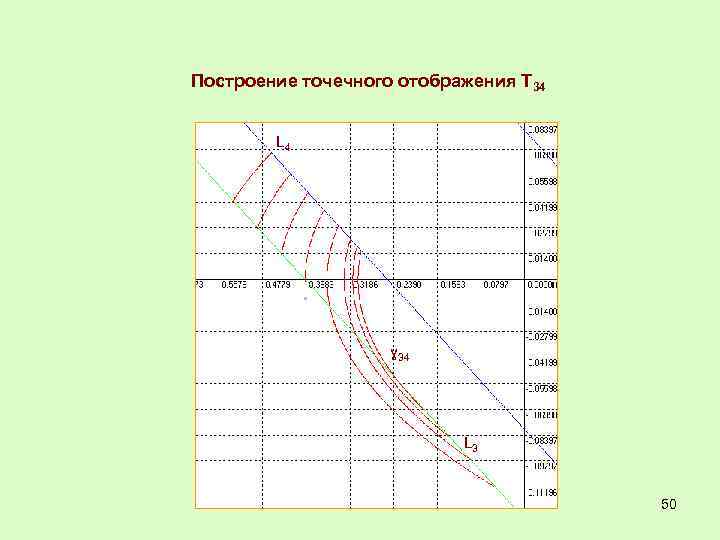
Построение точечного отображения Т 34 L 4 ɣ 34 L 3 50
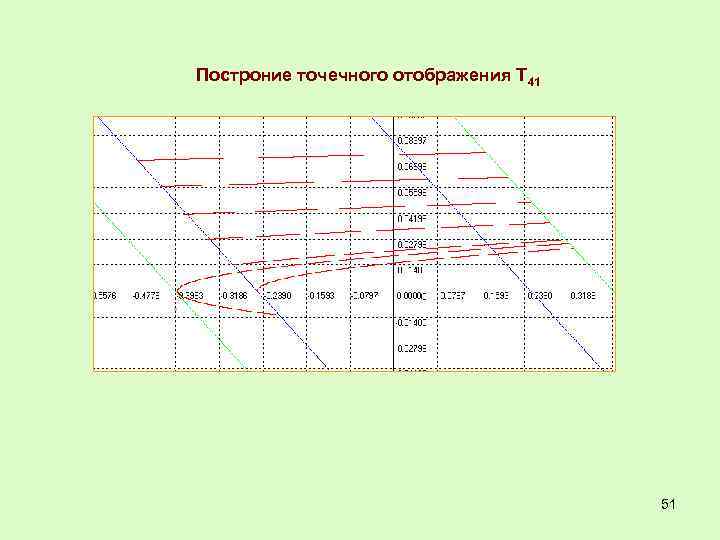
Построние точечного отображения Т 41 51
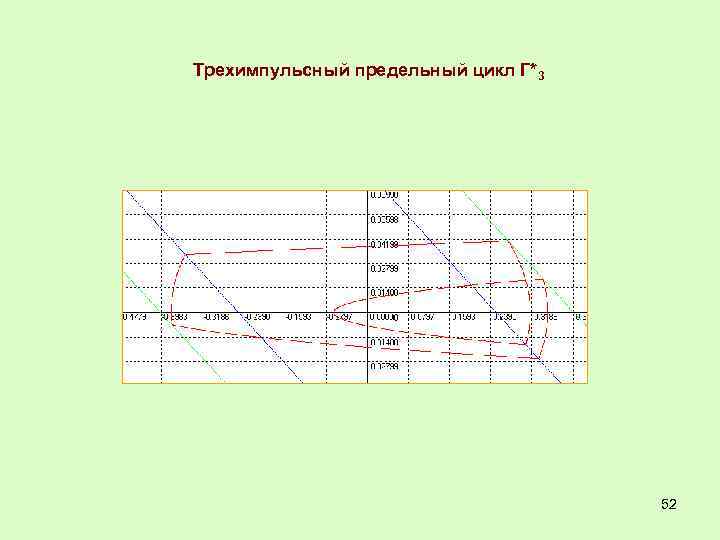
Трехимпульсный предельный цикл Г*3 52

Диаграмма Ламерея 53

54

55
09.09.2011 - АК1,2,4-91.ppt