Теорія Прийняття Рішень The Decision Theory лектор Дорохов

Теорія Прийняття Рішень The Decision Theory лектор: Дорохов Олександр Васильович к. т. н, доцент кафедри ІС

Алексей Кулаков Державотворення (исторический день - 24 августа 1991)

• В сессийном зале Верховной Рады - депутаты только что проголосовали за независимость Украины. • В левом углу - свиток с фамилиями депутатов, принимавших участие в историческом заседании. • На картине 70 наиболее активных депутатов Верховной Рады УССР • Депутаты покрывают трибуну флагом Украины. • Также на картине духовные символы нации - поэты и писатели, которые воспевали любовь к Украдине – Сковорода, Гоголь, Шевченко, Франко, Кулиш, Леся Украинка. • Всего на картине 100 действующих лиц. Размер холста - 5 х2 метра.

тема Метод аналітичної ієрархії – МАІ Analytic Hierarchy Process – AHP

Теоретичні питання 1. Основні етапи підходу аналітичної ієрархії 2. Шкала Сааті (Saaty) для парного порівняння відносної важливості критеріїв 3. Матриці порівнянь критеріїв та альтернатив за кожним критерієм окремо 4. Власні числа та власні вектори матриць 5. Розрахунок за методом аналітичної ієрархії

Література • • • Спеціальні розділи вищої математики: Нечіткі множини, нечіткі відношення, нечітка логіка та основи теорії наближених міркувань, двійкові динамічні системи, теорія випадкових функцій і процесів, прикладна теорія катастроф: Навч. посіб. / Б. В. Кузьменко, В. П. Лисенко. — К. : Фенікс, 2006. — 416 с. Теорія прийняття рішень: підручник / А. В. Катренко, В. В. Пасічник, В. П. Пасько. — К. : BHV, 2009. — 447 c. Теорія прийняття рішень. Основи теорії рішень: Метод. вказівки / Уклад. : В. В. Колодний; Вінниц. нац. техн. ун-т. — Вінниця, 2007. — 28 с. Theory of the analytic hierarchy process. P. 2. 1 = Теорія аналітичних ієрархічних процесів. Ч. 2. 1 / Thomas L. Saaty // Систем. дослідж. та інформ. технології. Введение в теорию и методы принятия решений: учеб. пособие / В. Д. Дмитриенко, В. А. Кравец, С. Ю. Леонов; Нац. техн. ун-т "Харьк. политехн. ин-т". — Х. , 2008. — 141 c.

Основні етапи підходу аналітичної ієрархії • Постановка завдання за методом AHP наступна: • Дано: загальна мета (ціль) вирішення завдання; N критеріїв оцінки альтернатив; n альтернатив. • Треба: вибрати найкращу альтернативу. • Підхід AHP складається з таких етапів: • 1. Представлення завдання у вигляді ієрархічної структури з декількома рівнями: цілі – критерії – альтернативи • 2. Виконання ОПР попарних порівнянь елементів кожного рівня та їх переведення за спеціальною таблицею в числа • 3. Розрахунок коефіцієнтів важливості для елементів кожного рівня та перевірка узгодженості міркувань ОПР • 4. Підрахунок кількісних індикаторів якості для кожної альтернативи та визначення найкращої з альтернатив

Приклад постановки завдання за методом AHP • Приклад - прийняття рішення з вибору приміщення для магазину (купівля або оренда приміщення). • Перший етап – структуризація задачі. • Припустимо, що ОПР – власник магазину відібрав з кількох можливих приміщень для магазину чотири варіанти: A, B, C, D. • Критерії вибору, наведені далі, визначає ОПР.

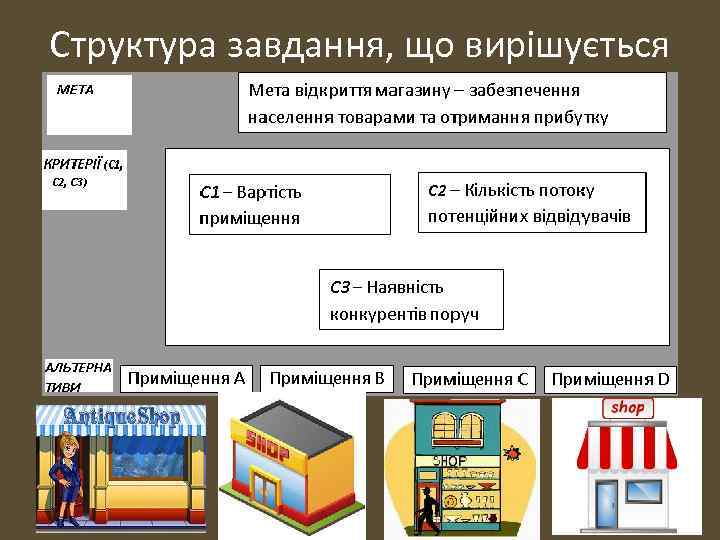Структура завдання, що вирішується

Критерії вибору, які визначає ОПР • С 1 – вартість приміщення – оцінюється в грошових одиницях, залежить від району міста, стану будинку та приміщення, транспортної доступністі … • С 2 – поток потенційних відвідувачів – кількість їх, що може відвідати магазин за годину, залежить від інтенсивності руху людей вулицею, щільності житлової забудови, наявності торговельних центрів, лікувальних закладів, зупинок транспорту… • С 3 – наявність конкурентів – підраховується кількість магазинів, розташованих поруч, тобто на відстані кількох хвилин ходьби

Оцінки альтернатив, які дає ОПР Варіанти A, B, C, D мають такі оцінки за критеріями С 1, С 2, С 3: • A (150 тис $; 40 покупців в годину ; 2 конкуренти), • B (70 тис $; 20 покупців в годину; 1 конкурент), • C (100 тис $; 50 покупців в годину; 5 конкурентів ), • D (140 тис $; 30 покупців в годину; 3 конкуренти ).

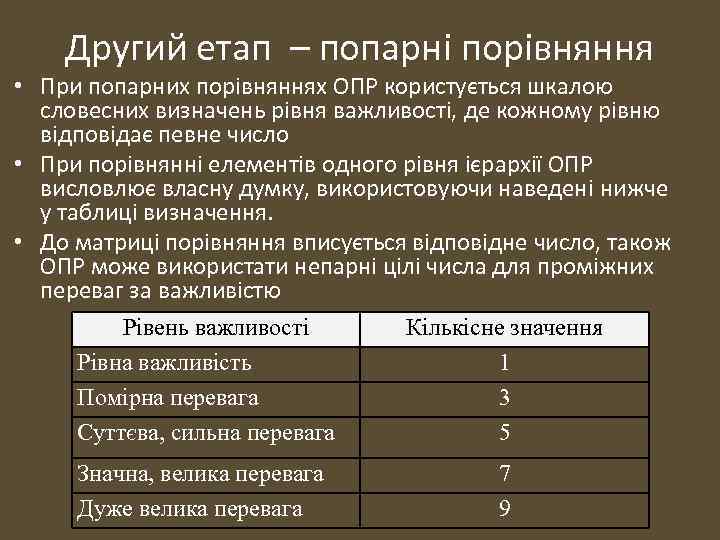Другий етап – попарні порівняння • При попарних порівняннях ОПР користується шкалою словесних визначень рівня важливості, де кожному рівню відповідає певне число • При порівнянні елементів одного рівня ієрархії ОПР висловлює власну думку, використовуючи наведені нижче у таблиці визначення. • До матриці порівняння вписується відповідне число, також ОПР може використати непарні цілі числа для проміжних переваг за важливістю Рівень важливості Рівна важливість Помірна перевага Суттєва, сильна перевага Кількісне значення 1 3 5 Значна, велика перевага Дуже велика перевага 7 9

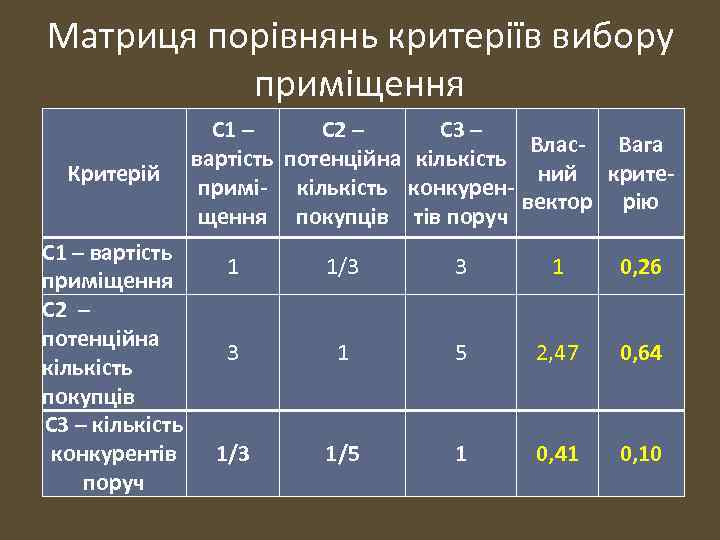Матриця порівнянь критеріїв вибору приміщення Критерій С 1 – вартість приміщення С 2 – потенційна кількість покупців С 3 – кількість конкурентів поруч С 1 – С 2 – С 3 – Влас- Вага вартість потенційна кількість ний критепримі- кількість конкуренвектор рію щення покупців тів поруч 1 1/3 3 1 0, 26 3 1 5 2, 47 0, 64 1/3 1/5 1 0, 41 0, 10

Матриця порівнянь важливості критеріїв вибору приміщення Матриця відповідає таким перевагам ОПР: • критерій С 2 «інтенсивність потоку потенційних відвідувачів» помірно переважає критерій С 1 «вартість приміщення» ; • критерій С 1 «вартість приміщення» помірно переважає критерій С 3 «наявність конкурентів поруч» ; • критерій С 2 «інтенсивність потоку потенційних відвідувачів» суттєво переважає критерій С 3 «наявність конкурентів поруч» . Далі аналогічно порівнюються альтернативи (конкретні приміщення A, B, C, D) за кожним критерієм окремо

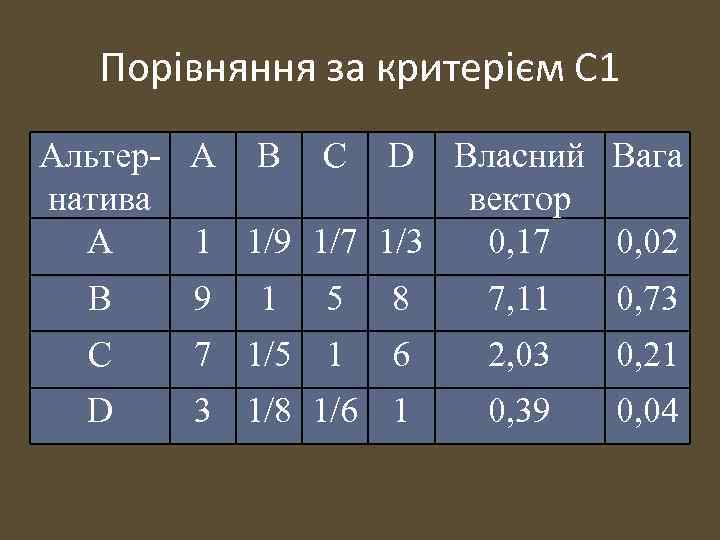Порівняння за критерієм С 1 Альтер- A B C D Власний Вага натива вектор A 1 1/9 1/7 1/3 0, 17 0, 02 B 9 1 5 8 7, 11 0, 73 C 7 1/5 1 6 2, 03 0, 21 D 3 1/8 1/6 1 0, 39 0, 04

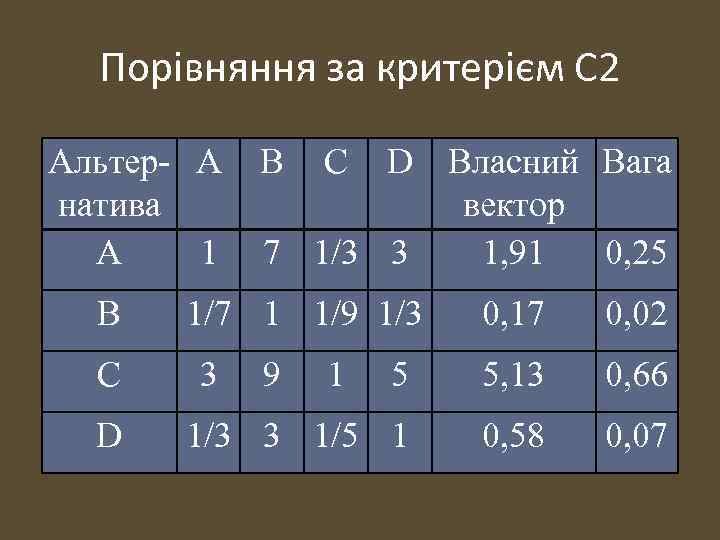Порівняння за критерієм С 2 Альтер- A натива A 1 B C D Власний Вага вектор 7 1/3 3 1, 91 0, 25 1/7 1 1/9 1/3 0, 17 0, 02 5 5, 13 0, 66 1/3 3 1/5 1 0, 58 0, 07 3 9 1

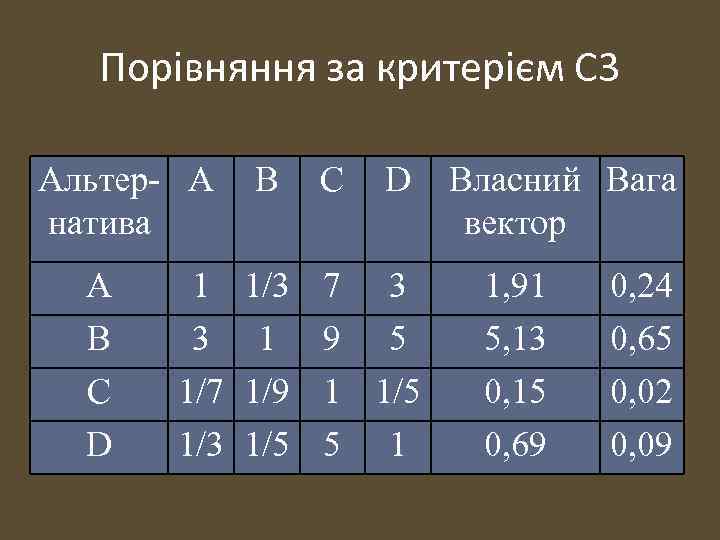Порівняння за критерієм С 3 Альтер- A натива A B C D 1 3 1/7 1/3 B 1/3 1 1/9 1/5 C D 7 3 9 5 1 1/5 5 1 Власний Вага вектор 1, 91 5, 13 0, 15 0, 69 0, 24 0, 65 0, 02 0, 09

Третій етап – розрахунок коефіцієнтів важливості • Таблиці дозволяють розрахувати коефіцієнти важливості відповідних елементів ієрархічного рівня. • Для цього необхідно обчислити власні вектори матриці, а далі пронормувати їх. • Розрахунок проводиться так: добувається корінь n-го степеню (n – розмірність матриці порівнянь) із добутку елементів кожного рядка матриці.

Розрахунок коефіцієнтів важливості Критерій С 1 1 С 2 3 С 3 1/3 • • • С 2 1/3 1 1/5 С 3 3 5 1 Власний вектор Вага критерію 1 0, 26 2, 47 0, 64 0, 41 0, 10 маємо добутки елементів кожного рядка матриці: для першого рядка – 1 × 1/3 × 3 = 1 для другого рядка – 3 × 1 × 5 = 15 для третього рядка – 1/3 × 1/5 × 1 = 0, 0666. обчислюємо корень третього ступеню, бо розмірність матриці дорівнює трьом - це те ж саме що й зведення до ступеня 1/3 Маємо значення власних векторів: для першого рядка – 1 для другого рядка – 2, 47 для третього рядка – 0, 41.

• Добування кореню третього степеню в Excel • Далі розраховані значення власних векторів нормуються. Нормування цих чисел дає ваги критеріїв wi для кожного рядка матриці: w 1 = 1 : (1+2, 47+0, 41) = 0, 26 w 2 = 2, 47 : (1+2, 47+0, 41) = 0, 64 w 3 = 0, 41 : (1+2, 47+0, 41) = 0, 10 • У такий же спосіб на основі таблиць попарно порівнюються кожна з альтернативи A, B, C, D окремо за кожним з критерієв С 1, С 2, С 3 • В таблицях наведені вже обчислені ваги альтернатив за кожним критерієм окремо

Четвертий етап – визначення найкращої альтернативи • Проводиться розрахунок якості кожної альтернативи за формулою: V j = Σ wi Vji • де V j – показник якості j-ї альтернативи; • wi – вага i-го критерію; • Vji – відносна оцінка j-ї альтернативи по i-му критерію • • • Для кожної альтернативи A, B, C, D маємо: для A - V(А) = 0, 26× 0, 02 + 0, 64× 0, 25 + 0, 10× 0, 24 = 0, 19 для B – V( В) = 0, 26× 0, 73 + 0, 64× 0, 02 + 0, 10× 0, 65 = 0, 38 для C – V(С) = 0, 26× 0, 21 + 0, 64× 0, 66 + 0, 10× 0, 02 = 0, 48 для D – V(D) = 0, 26× 0, 04 + 0, 64× 0, 07 + 0, 10× 0, 09 = 0, 06 Отже, альтернатива C – найкраща.

Дякую за увагу!