Теория пределов Лекция 1 2 Бесконечная

Теория пределов Лекция 1

2

Бесконечная числовая последовательность n Определение Бесконечная числовая последовательность – совокупность чисел вида где каждое значение называется членом (элементом) последовательности, а число n – его номером. Замечание Последовательность считается заданной, если задан способ вычисления любого его члена по известному номеру Если каждому натуральному числу n по некоторому закону поставлено в соответствие определенное число an , то говорят, что задана числовая последовательность 3

Геометрическая интерпретация числовой последовательности 4

Числа a 1, a 2…an называются членами последовательности, а число an называется общим членом или n-ым членом данной последовательности. Например: 1 2

Определение. Пусть x 0 R , > 0. Интервал (x 0 - , x 0+ ) будем называть -окрестностью точки x 0. Обозначение: U(x 0, )= (x 0 - , x 0+ )= {x R | |x - x 0|< }. 6

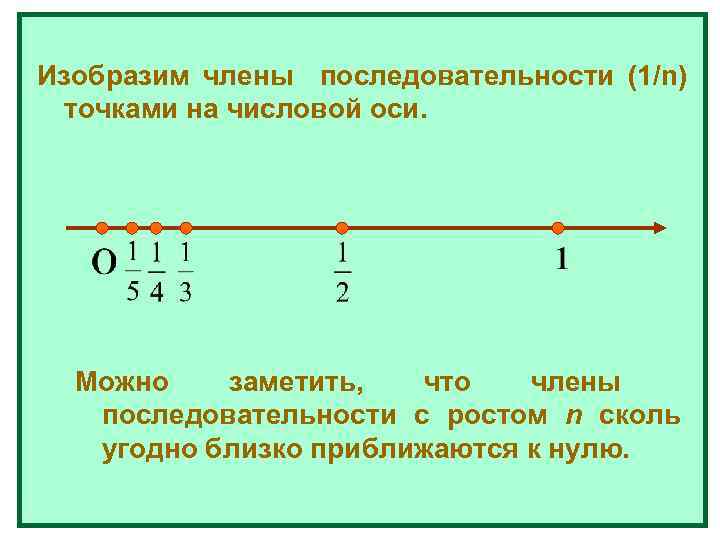
Изобразим члены последовательности (1/n) точками на числовой оси. Можно заметить, что члены последовательности с ростом n сколь угодно близко приближаются к нулю.

Последовательность {an} называется ограниченной сверху (снизу), если существует такое число М (m), что любой элемент этой последовательности удовлетворяет неравенству:

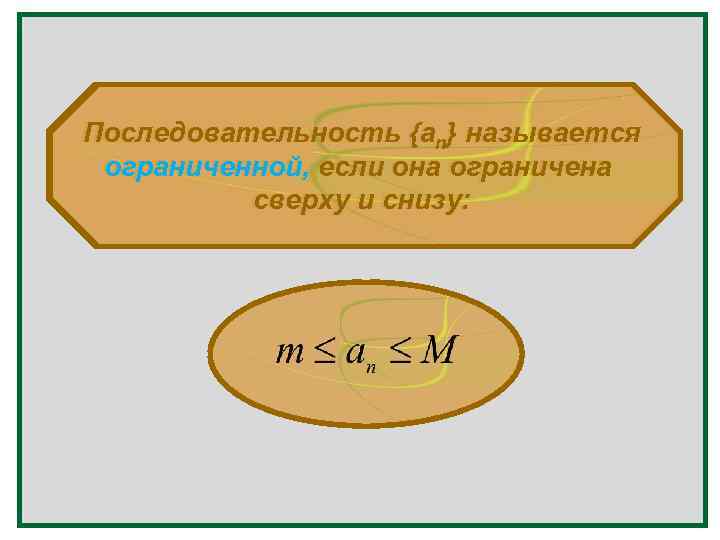
Последовательность {an} называется n ограниченной, если она ограничена сверху и снизу:

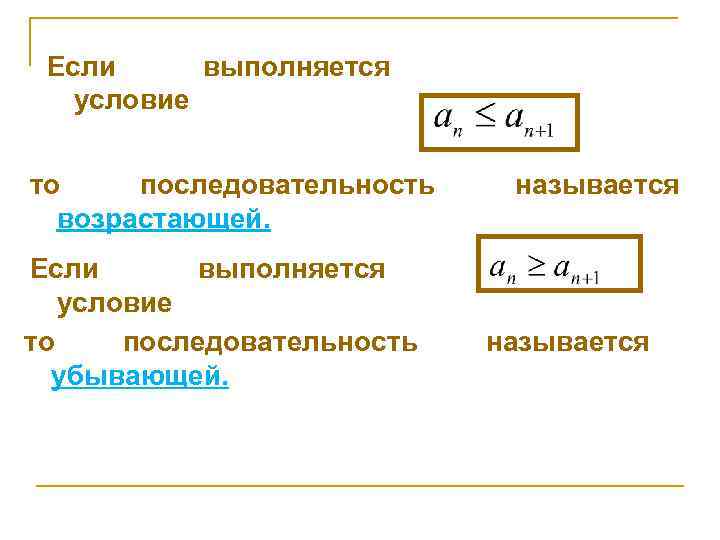
Если выполняется условие то последовательность возрастающей. Если выполняется условие то последовательность убывающей. называется

Числовые последовательности Определение. Последовательность называется n ограниченной сверху, если ; n ограниченной снизу, если ; n ограниченной, если n неограниченной, если ; n монотонно возрастающей, если ; n строго монотонно возрастающей, если ; n монотонно убывающей, если ; n строго монотонно убывающей, если ;

Предел последовательности 12

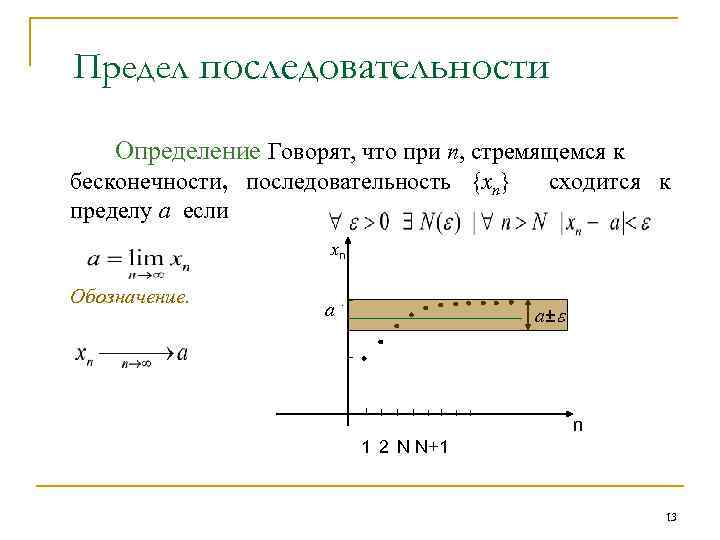
Предел последовательности Определение Говорят, что при n, стремящемся к бесконечности, последовательность {xn} сходится к пределу a если Обозначение. xn aa a± n 1 2 N N+1 13

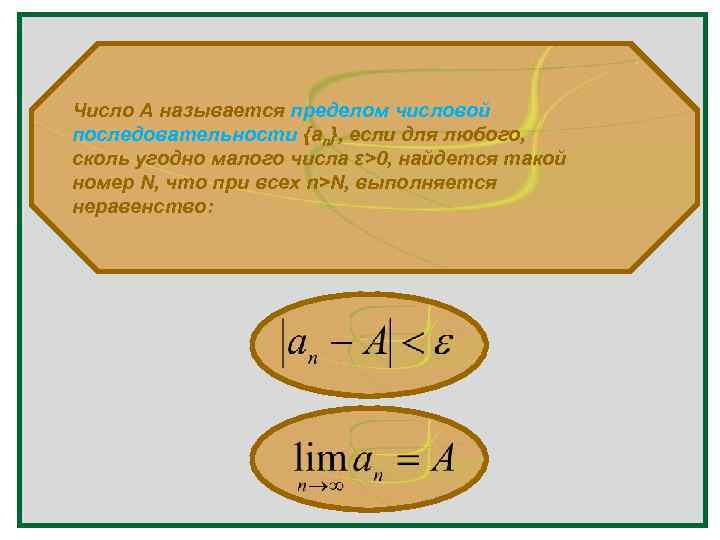
Число А называется пределом числовой последовательности {an}, если для любого, сколь угодно малого числа ε>0, найдется такой номер N, что при всех n>N, выполняется неравенство:

Геометрическая интерпретация предела последовательности последовательность имеет предел, если «Какого бы ни было положительное число , все элементы последовательности, начиная с некоторого номера N+1, находятся внутри -окрестности точки а» . Пример что для выполняется 15

16

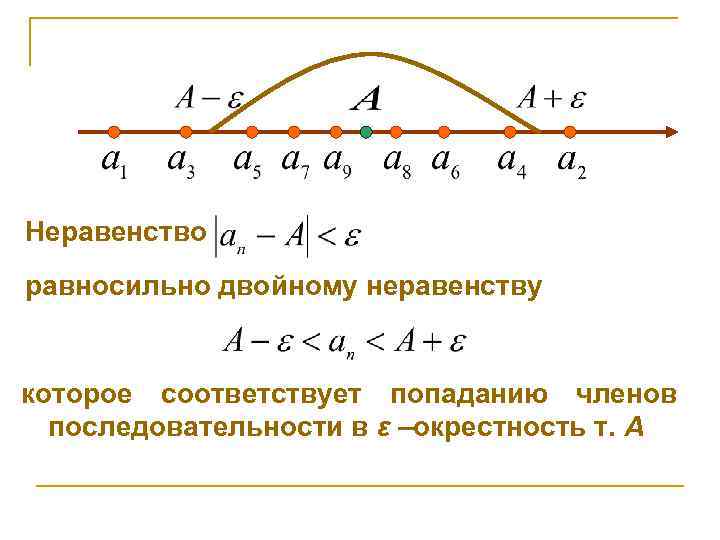
Неравенство равносильно двойному неравенству которое соответствует попаданию членов последовательности в ε –окрестность т. А

Т. е. число А есть предел числовой последовательности {an}, если для любого, сколь угодно малого числа ε>0, найдется такой номер N, начиная с которого все члены последовательности будут заключены в ε – окрестности точки А, какой бы узкой она не была. Вне этой окрестности может быть только конечное число членов последовательности.

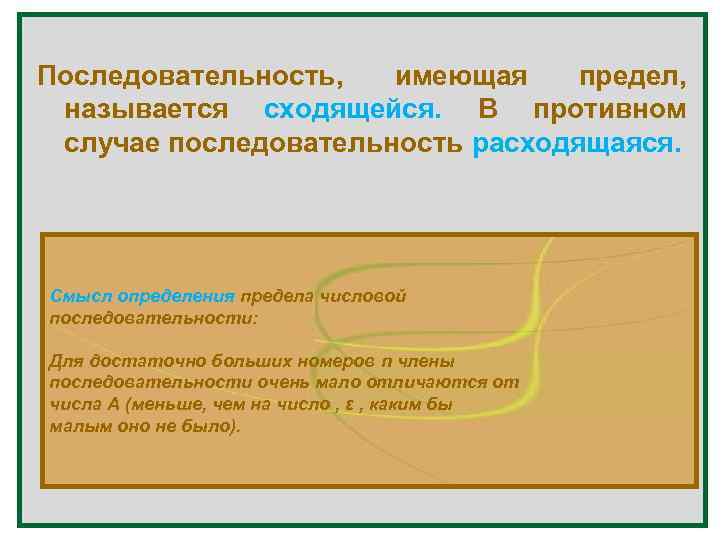
Последовательность, имеющая предел, называется сходящейся. В противном случае последовательность расходящаяся. Смысл определения предела числовой последовательности: Для достаточно больших номеров n члены последовательности очень мало отличаются от числа А (меньше, чем на число , ε , каким бы малым оно не было).

ПРИМЕР Дана последовательность 3 Показать, что предел этой последовательности равен 1.

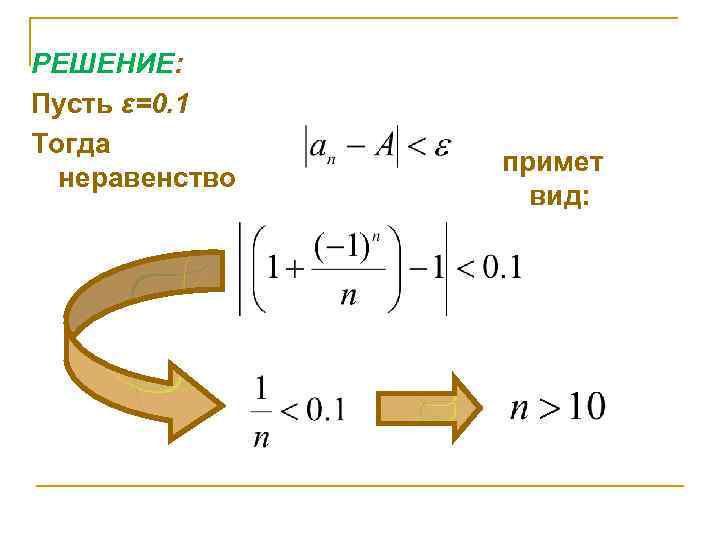
РЕШЕНИЕ: Пусть ε=0. 1 Тогда неравенство примет вид:

Если ε=0. 01, то неравенство выполняется при Для любого ε >0, неравенство выполняется при Т. е. для любого ε >0 существует номер Что для всех n>N, выполняется неравенство:

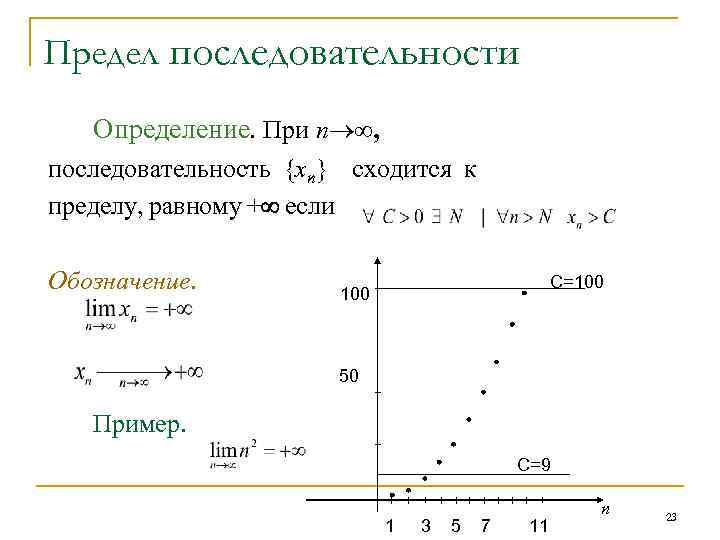
Предел последовательности Определение. При n , последовательность {xn} сходится к пределу, равному + если Обозначение. 100 C=100 50 Пример. C=9 1 3 5 7 11 n 23

Примеры вычисления пределов Найти предел последовательности: 1) Решение. ; 1) Имеем: . 24

Примеры вычисления пределов Найти предел последовательности: 2) Решение. Применив правило «предел суммы» , получим: . 25

Примеры вычисления пределов Вычислить Решение. . прием: числитель, и знаменатель дроби делим почленно на наивысшую из имеющихся в числителе или знаменателе степень переменной. 26

27

n Замечание Последовательность может и не иметь предела Замечание Последовательность, предел которой существует, называется сходящейся Определение Последовательность называется ограниченной, если при всех Пример ограниченная последовательность 28

n Определение Последовательность называется монотонно возрастающей, если при всех n каждый ее член больше предшествующего, т. е. монотонно убывающей, если при всех n каждый ее член меньше предшествующего, т. е Пример -Последовательность возрастает, -ограничена сверху монотонно убывающая 29

Теорема Вейерштрасса (о существовании предела монотонной последовательности) 30

n Карл Вейерштрасс 1815 -1897 выдающийся немецкий математик, «отец современного анализа» . сформулировал логическое обоснование анализа на основе построенной им теории действительных (вещественных) чисел и языка 31

Существует последовательности, пределы которых следует запомнить (1) ; (2) , ( (3) если ; предел стационарной последовательности равен значению любого члена этой последовательности ). 32

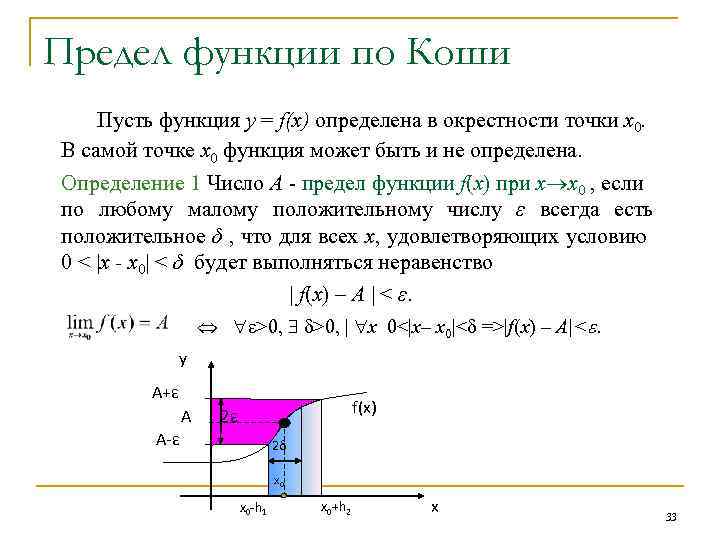
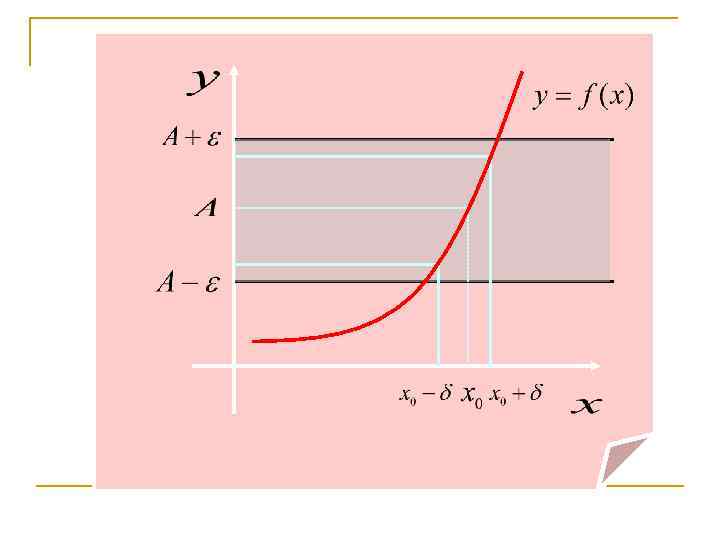
Предел функции по Коши Пусть функция у = f(x) определена в окрестности точки x 0. В самой точке x 0 функция может быть и не определена. Определение 1 Число А - предел функции f(x) при x x 0 , если по любому малому положительному числу ε всегда есть положительное δ , что для всех х, удовлетворяющих условию 0 < |x - x 0| < δ будет выполняться неравенство | f(x) – A | < ε. >0, | x 0<|x– x 0|< =>|f(x) – А|<. y A+ε A f(x) 2ε A-ε 2δ x 0 -h 1 x 0+h 2 x 33

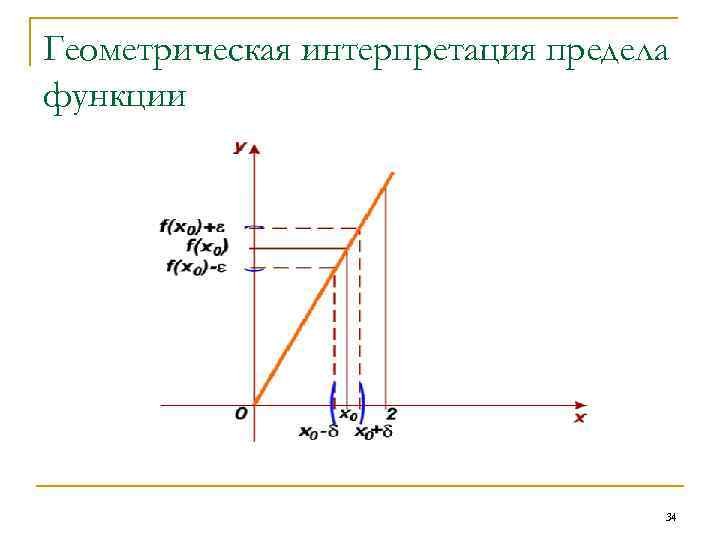
Геометрическая интерпретация предела функции 34

35

Пример n Доказать, что Пусть задано для того чтобы необходимо 36

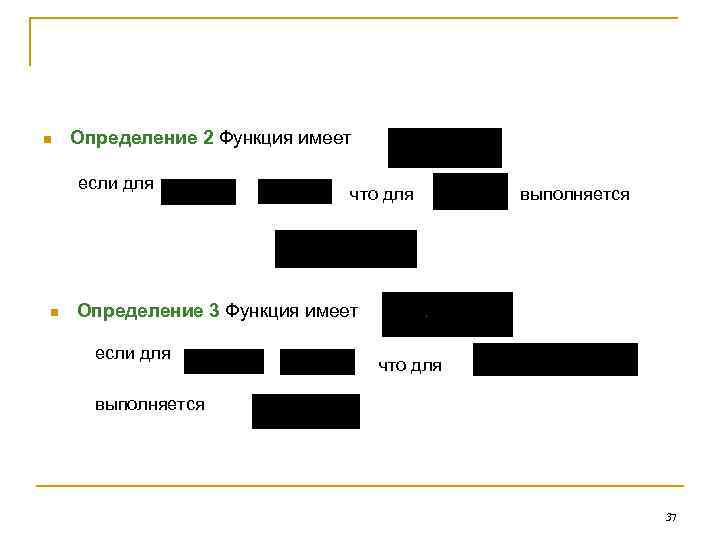
n Определение 2 Функция имеет если для n что для выполняется Определение 3 Функция имеет если для что для выполняется 37

38

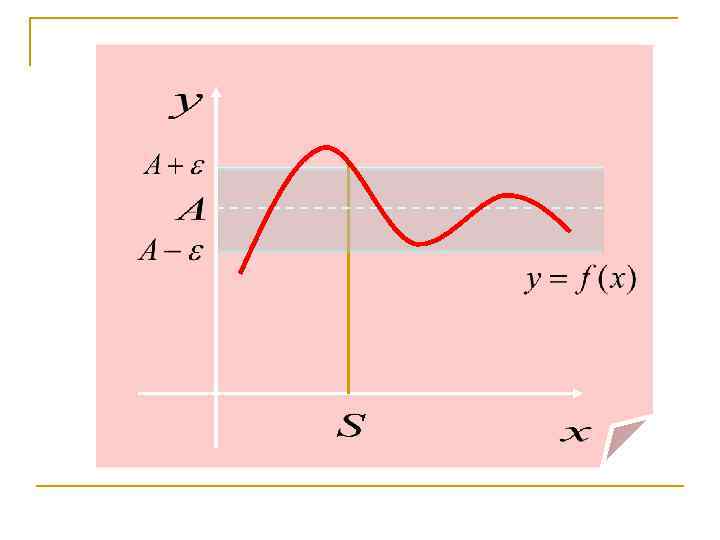
Доказать, что будет выполняться при выполняется при ε=0. 1 что для всех х, таких что |x-1|<δ, выполняется неравенство: выполняется при

Определение предела не требует существования функции в самой точке x 0, т. к. рассматриваются значения функции в некоторой окрестности точки x 0. Т. е. рассматривая предел мы предполагаем, что но не достигает значения x 0.

43

Бесконечно-малые последовательности 44

n Пример б. м. при функция является бесконечно малой не является б. м. 45

Свойства бесконечно-малых последовательностей Если последовательности {xn} и {yn} бесконечно-малые, то {xn yn} тоже бесконечно-малая последовательность. Следствие. Сумма и разность любого конечного числа б. м. п. есть также б. м. п. 1. 2. Произведение б. м. п. на ограниченную последовательность есть б. м. п. 3. Б. м. п. ограничена. 4. Пусть {xn} б. м. п. и n xn 0. Тогда {1/xn} есть б. б. 5. Пусть {xn} б. б. п. и n xn 0. Тогда {1/xn} есть б. м. 46

Свойства б. б. 47

Свойства сходящихся последовательностей 1. Теорема (о единственности предела). Если последовательность имеет предел, то он единственный. 2. Для того, чтобы последовательность {xn} была сходящейся, необходимо и достаточно, чтобы ее можно было представить в виде x n = a + n , где , а { n} б. м. 3. Сходящаяся последовательность ограничена. 4. Если , то, начиная с некоторого номера n =N, последовательность {1/yn} ограничена. 48

Свойства сходящихся последовательностей 5. Если последовательности {xn} и {yn} сходящиеся, то {xn yn} тоже сходящаяся последовательность и 6. Если {xn} сходящаяся последовательность, то {c xn} тоже сходится и . 7. Если последовательности {xn} и {yn} сходящиеся, то {xn yn} тоже сходящейся последовательность и, 8. Пусть последовательности {xn} и {yn} сходящиеся, причем . Тогда {xn/yn} есть также сходящаяся последовательность и . 49

50

Свойства пределов 4. a) b) c) d) Если функции f(x) и g(x) имеют предел при х x 0 , то их сумма, разность, произведение и частное имеют предел при х x 0, причем ; Если функция f(x) имеет предел при х x 0, то произведение с*f(x) имеет предел при х x 0, с – константа, причем . 51

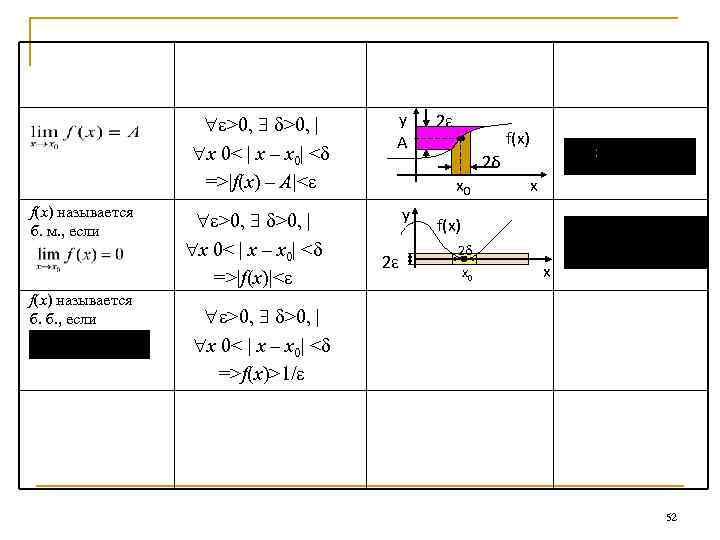
обозначение предела краткая запись определения >0, | x 0< | х – x 0| < =>|f(x) – A|< f(x) называется б. м. , если f(x) называется б. б. , если >0, | x 0< | х – x 0| < =>|f(x)|< Геометрическая иллюстрация y A 2ε f(x) 2δ x 0 y 2ε пример x f(x) 2δ x 0 x >0, | x 0< | х – x 0| < =>f(x)>1/ 52

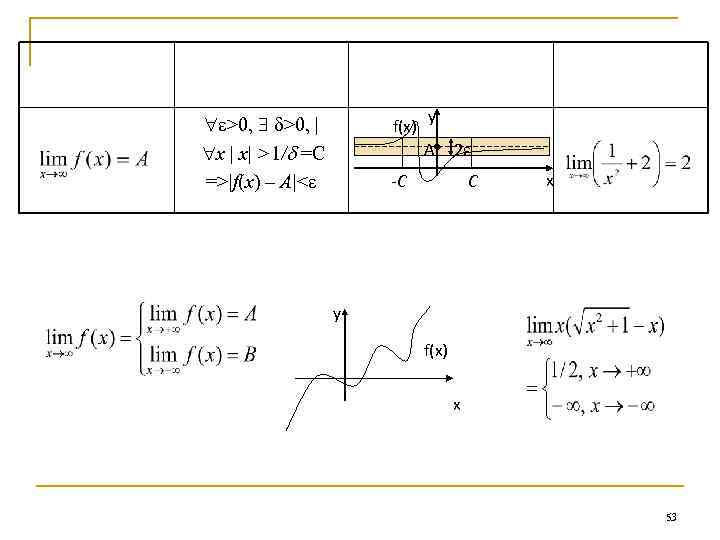
обозначение предела краткая запись определения Геометрическая иллюстрация >0, | x | х| >1/ =C =>|f(x) – A|< f(x) пример y A 2ε C -C x y f(x) x 53

Свойства пределов 1. Если предел функции f(x) при х x 0 существует, то он единственный. 2. Если функция f(x) при х x 0 имеет конечный предел, то она ограничена в некоторой окрестности точки x 0. 3. Теорема. Функция имеет предел тогда и только тогда, когда ее можно представить как сумму постоянной, равной этому пределу и бесконечно малой величины. 54

Свойства б. м. функции Сумма, разность, произведение двух б. м. при x x 0 есть функция б. м. при x x 0. 2. Пусть (x) - б. м. при x x 0, f(x) – ограниченна , тогда (x) f(x) – б. м. при x x 0. 1. Если (x) - б. м. при x x 0, то с (x) - б. м. при x x 0, с-константа. v (Связь между б. м. и б. б. ) Если функция у = f(x) – б. м. при x x 0 и f(x) 0 в некоторой окрестности точки x 0, то функция y = 1/f(x) – б. б. при x x 0. Если функция у = f(x) - б. б. при x x 0, и f(x) 0 в некоторой окрестности точки x 0, то функция y = 1/f(x) – б. м. при x x 0. 1. 55

56