Теория подобия и моделирования Подобие Подобие геометрическое скоростей

Зарегистрируйтесь, чтобы просмотреть полный документ!

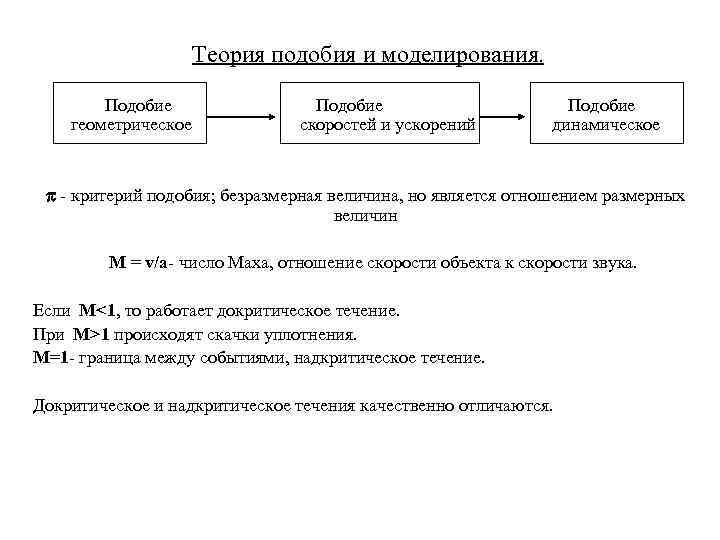
Теория подобия и моделирования. Подобие Подобие геометрическое скоростей и ускорений Подобие динамическое - критерий подобия; безразмерная величина, но является отношением размерных величин M = v/a- число Маха, отношение скорости объекта к скорости звука. Если М<1, то работает докритическое течение. При М>1 происходят скачки уплотнения. М=1 - граница между событиями, надкритическое течение. Докритическое и надкритическое течения качественно отличаются.

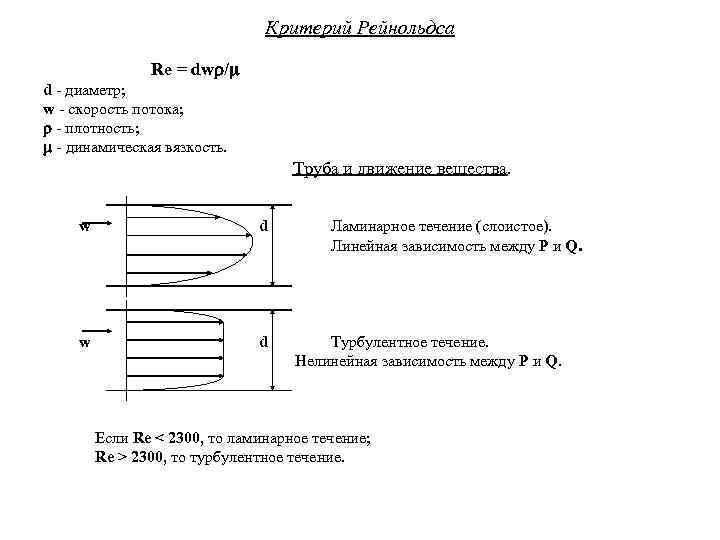
Критерий Рейнольдса Re = dw / d - диаметр; w - скорость потока; - плотность; - динамическая вязкость. Труба и движение вещества. w w d Ламинарное течение (слоистое). Линейная зависимость между P и Q. d Турбулентное течение. Нелинейная зависимость между P и Q. Если Re < 2300, то ламинарное течение; Re > 2300, то турбулентное течение.

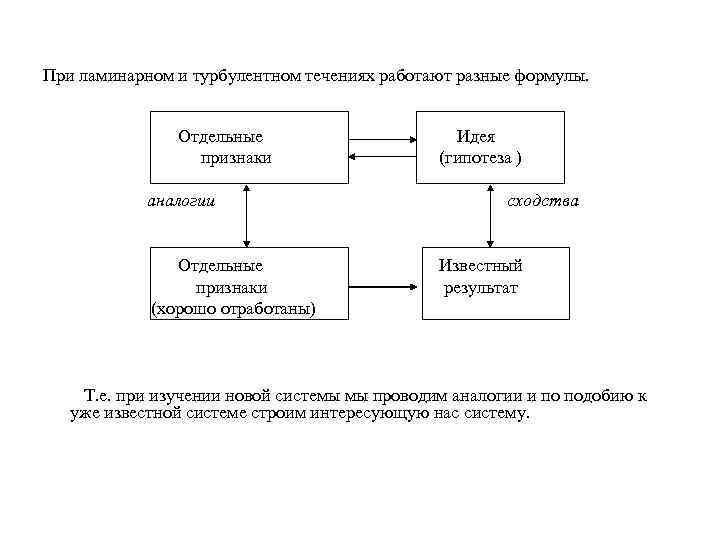
При ламинарном и турбулентном течениях работают разные формулы. Отдельные признаки аналогии Отдельные признаки (хорошо отработаны) Идея (гипотеза ) сходства Известный результат Т. е. при изучении новой системы мы проводим аналогии и по подобию к уже известной системе строим интересующую нас систему.

Методы получения критериев подобия. Метод основан на использовании: а). - теоремы (теоремы Букингема) б). Метода интегральных аналогов В основе лежит теория размерности. A = {A}[A] - единицы размерности, т. е. A = {30}[км/час] Есть единицы основные и произвольные.

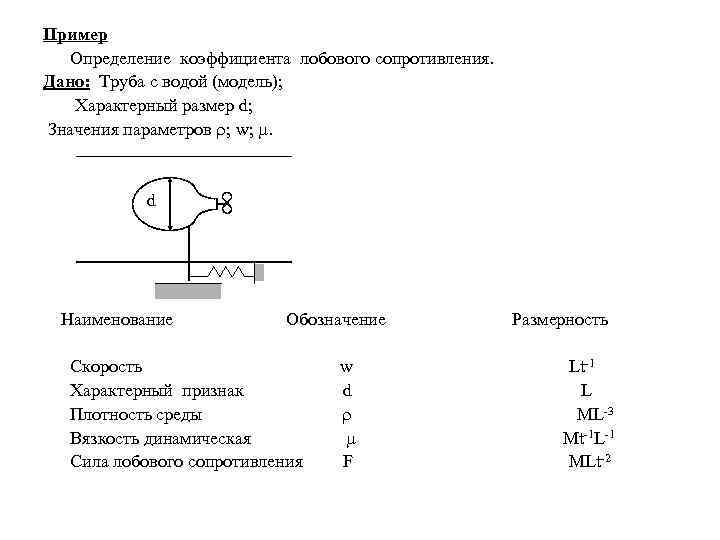
Пример Определение коэффициента лобового сопротивления. Дано: Труба с водой (модель); Характерный размер d; Значения параметров ; w; . d Наименование Обозначение Размерность Скорость w Lt-1 Характерный признак d L Плотность среды ML-3 Вязкость динамическая Mt-1 L-1 Сила лобового сопротивления F MLt-2

Есть некая функция, которая определяет силу лобового сопротивления как (wa, db, c, λ) = F Определим размерность ([Lt-1]a, [L]b, [ML-3]c, [Mt-1 L-1] λ) = [MLt-2] M: c + λ = 1 L: a + b - 3 c - λ = 1 t: - a - λ = -2 Решаем систему уравнений и получаем c = 1 - λ a = 2 - λ 2 - λ + b - 3 + 3 λ - λ = 1 b = 2 - λ Перепишем исходную формулу в несколько ином виде (w 2 - λ, d 2 - λ, 1 - λ, λ) = F т. е. можем записать F/w 2 d 2 = ( /wd ) = (1/Re)

- теорема Всякое полное уравнение физического процесса записанное в определенной системе единиц может быть представлена в виде зависимости между критериями подобия, т. е. безразмерных соотношений, составленных из входящих в уравнение переменных и параметров. f(P 1, P 2, . . . , Pi, . . . , Pk, . . . , Ps, . . . , Pm) = 0 1 i k k+1 s m f(P 1/P 01; P 2/P 02, . . . ; Pi/P 0 i, . . . ; Pk/P 0 k, . . . ; Ps/P 0 s, . . . ; Pm/P 0 m)=0 Основные и производные единицы. Производные можно выразить через основные. Для этого надо: а) Выбрать те параметры, которые являются независимыми. Б) Выразить зависимые через независимые. Имеем матрицу размерностью [m n], в которой число строк больше числа столбцов (m > n). Ранг не больше n.

Пусть P 1, . . . , Pk - независимые параметры; Pk+1, . . . , Pm - зависимые параметры. Pk+1, . . . , Pm. следует выразить через P 1, . . . , Pk Тогда получим f(1, . . . , s-k, . . . , m-k) = 0 Каждый параметр P выражается в виде Р = {Р}[Р] где {Р}- число, [Р] - размерность. [P 1] = [a 1, b 1, . . . , q 1] = [P 01] [P 2] = [a 2, b 2, . . . , q 2] = [P 02] . [Pi] = [a i, b i, . . . , q i] = [P 0 i] . [Pk] = [a k, b k, . . . , q k] = [P 0 k] k q q - количество независимых параметров.

[P 0, k+1] = k+1{[P 01], . . . , [P 0 k]} . . . [P 0, s] = s{[P 01], . . . , [P 0 k]} . . . [P 0, n] = n{[P 01], . . . , [P 0 k]} Определим зависимости k+1, . . . , s, . . . , n ln[P 01] = 1 ln[a] + 1 ln[b] +. . . + 1 ln[q] ln[P 02] = 2 ln[a] + 2 ln[b] +. . . + 2 ln[q] . . ln[P 0 k] = kln[a] + kln[b] +. . . + kln[q] D - определитель 1 1 . . . 1 2 2 . . . 2 = D . k k . . . k ln[P 01] ln[P 02] . . . ln[P 0 k] ln[a] = (ln[P 01])A 11/D(ln[P 02])A 21/D. . . (ln[P 0 k])Ak 1/D Ak 1 - определить получаемый из определителя D путем вычеркивания k-ой строки и 1 го столбца. k ln[a] = (Ai 1/D)ln[P 0 i] i=1

Пусть k = q ln[a] = ln[b] = . . ln[q] = Определяем [a], [b], . . . , [q] [a] = [P 01]A 11/D[P 02]A 21/D. . . [P 0 k]Ak 1/D [b] = . [q] = Полученные выражения подставим в формулы [P 0, k+1] = [P 01]D 1, k+1/D[P 02]D 2, k+1/D. . . [P 0 k]Dk, k+1/D . . [P 0, s] = [P 01]D 1, s/D[P 02]D 2, s/D. . . [P 0 k]Dk, s/D . . [P 0, m] = [P 01]D 1, m/D[P 02]D 2, m/D. . . [P 0 k]Dk, m/D Di, k+1 - определитель, в котором i-ая строка заменена (k+1) строкой из формул размерности.

k [P 0, s] = [P 0 i]Di, s/D i=1 Di, k+1/D = xi Di, s/D = yi Di, m/D = zi k [P 0, k+1] = [P 0 i]xi = 1 i=1 k [P 0, s] = [P 0 i]yi = s-k i=1 k [P 0, m] = [P 0 i]zi = m-k i=1

Пусть P 1 = P 01 P 2 = P 02 . . Pk = P 0 k k xi, . . . , P / [P ]yi, . . . , P / [P ]zi) = 0 f(1, . . . , 1, Pk+1/ [P 0 i] s 0 i m 0 i i=1 1 = ( 2, . . . , m-k) f(1, . . . , s-k, . . . , m-k) Реальность 1 2 m-k P 1, P 2, . . . , Pk, . . . , Pm - подобие сил. Модель 1 m-k

Метод интегральных аналогов. Для получения критериев подобия по методу интегральных аналогов необходимо знать уравнения системы или процесса. Если все члены уравнения разделить на один из них, то получим уравнение в безразмерной форме (Фурье - все члены уравнения имеют одну и ту же размерность). Пример Уравнение Навье-Стокса. V- скорость потока в точке. F - объемная или массовая сила Р - давление - плотность жидкости - кинетическая вязкость - лапласиан или дифференциальный оператор второго порядка - оператор набла = - скалярное произведение

- старая координата

а). Пренебрегаем индексом 1 б). Разделим члены уравнения на - число подобия Струхаля - число подобия Фруда - число подобия Эйлера - число подобия Рейнольдса

Скачать презентацию Теория подобия и моделирования Подобие Подобие геометрическое скоростей

теория моделирования и подобия.ppt

Количество слайдов: 15