ТЕОРИЯ ОТРАСЛЕВЫХ РЫНКОВ Лекция 5 -6 Модели олигополистических

ТЕОРИЯ ОТРАСЛЕВЫХ РЫНКОВ Лекция 5 -6. Модели олигополистических рынков и теория игр

Содержание лекции 1. Общая характеристика олигополистической структуры 2. Кооперированная олигополия (сговор и картели) 3. Независимое поведение: объёмная конкуренция. Модель дуополии Курно 4. Модель дуополии Штакельберга 5. Независимое поведение: ценовая конкуренция. Модель Бертрана 6. Модель Эджуорта 7. Методы теории игр для анализа поведения олигополии Цой Р. А. , РГЭУ (РИНХ) - 2014 2

Олигополия тип рыночной структуры несовершенной конкуренции, в которой доминирует крайне малое количество фирм. Олигополия отличается от других типов несовершенной конкуренции тем, что имеет место взаимозависимость фирм в отрасли. Олигополисты - не только конкуренты, но и одновременно негласные партнеры. При небольшом количестве производителей в отрасли фирмеолигополисту необходимо планировать свою стратегию с учетом поведения других участников рынка. Оказывает на развитие экономики двоякое воздействие. С одной стороны, выступает антиподом монополии, с другой - препятствует развитию совершенной конкуренции. Цой Р. А. , РГЭУ (РИНХ) - 2014 3

Признаки олигополии Небольшое количество фирм (обычно до 10, хотя может быть и больше) и большое количество покупателей; Товар, реализуемый олигополистическими фирмами, может быть и дифференцированным и стандартизированным; Возможность воздействовать на цену, что предполагает убывающую кривую спроса; Ценообразование на рынках олигополии предполагает взаимозависимость фирм, принятии решений относительно их поведения на рынке; Наличие существенных барьеров входа на рынок. Цой Р. А. , РГЭУ (РИНХ) - 2014 4

Поведение фирм в условиях олигополии Каждая из фирм олигополистов при формировании своей экономической политики вынуждена принимать во внимание реакцию со стороны конкурентов. Кривая спроса на продукцию отдельного олигополиста принятии стратегических решений, как правило, неизвестна, - решения принимаются исходя из предположений олигополистов относительно реакции конкурентов на действия друга. При олигополии цены меняются не столь часто как при совершенной конкуренции (жёсткость ценообразования), обычно через какие-нибудь промежутки времени и на значительную величину, что связано со взаимозависимостью фирм. Цой Р. А. , РГЭУ (РИНХ) - 2014 5

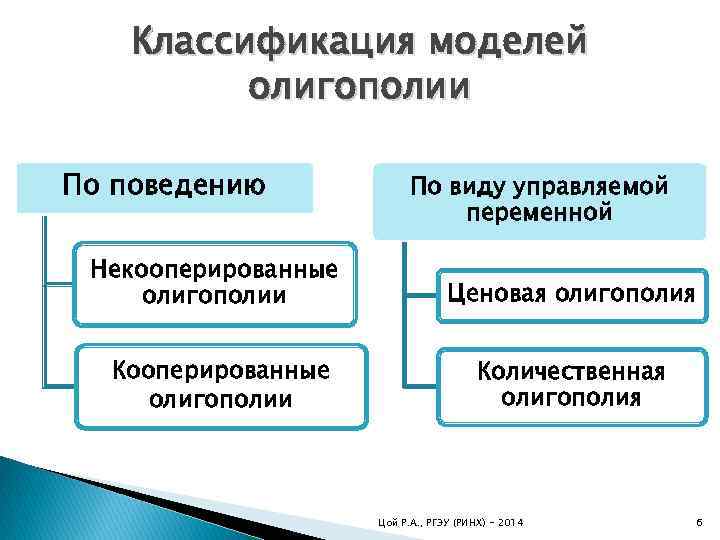Классификация моделей олигополии По поведению По виду управляемой переменной Некооперированные олигополии Ценовая олигополия Кооперированные олигополии Количественная олигополия Цой Р. А. , РГЭУ (РИНХ) - 2014 6

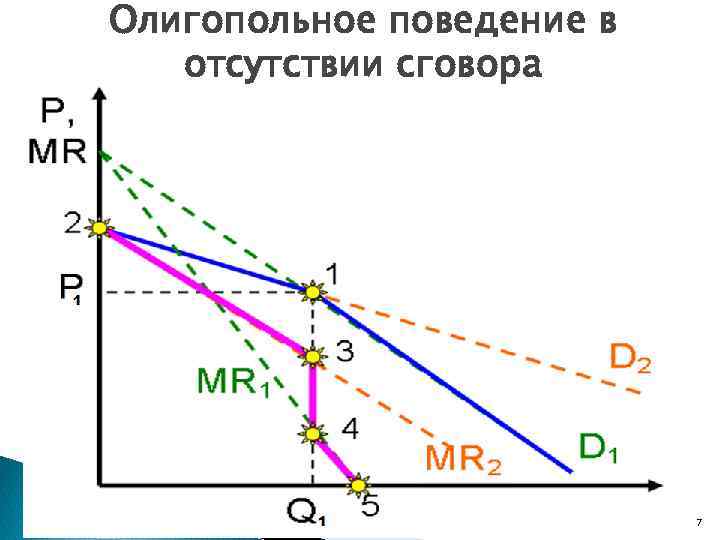Олигопольное поведение в отсутствии сговора Цой Р. А. , РГЭУ (РИНХ) - 2014 7

Ценовая политика Как правило, фирме невыгодно повышать цены на свои товары и услуги, поскольку велика вероятность того, что другие фирмы не последуют за первой, и потребители “перейдут” к компаниисопернику. Если же фирма понижает цены на свою продукцию, то, чтобы не потерять клиентов, конкуренты, обычно, следуют за понизившей цены компанией, также снижая цены на предлагаемые ими товары: происходит “гонка за лидером”. Таким образом, между олигополистами нередко случаются так называемые ценовые войны, в которых фирмы устанавливают на свою продукцию цену, не большую чем у конкуренталидера. Цой Р. А. , РГЭУ (РИНХ) - 2014 8

Теории олигополистического ценообразования Модель Курно Модель Чемберлина Модель Бертрана Модель Гутенберга Модель Эджуорта Модель Штакельберга Цой Р. А. , РГЭУ (РИНХ) - 2014 9

Модель дуополии Курно Анализ дуополии как простейшей формы Предпосылки 1)олигополии впервые был осуществлен в Две фирмы производят однородный 1838 товар. г. французским экономистом 2)Огюстеном Курно. кривая рыночного Фирмам известна Эта модель описывает рыночное равновесие спроса. условиях некооперированной 3)в. Фирмы принимают решения о олигополии. производстве независимо друг от друга и одновременно. 4) Каждая из фирм предполагает выпуск конкурента постоянным. Цой Р. А. , РГЭУ (РИНХ) - 2014 10

Модель дуополии Курно Отраслевой спрос, представлен линейной функцией: Р = a – b*Q (1) где a, b – положительные константы, Q = q 1+q 2 – объем рыночного спроса, складывается из объемов предложения первой (q 1) и второй (q 2) фирм при цене P. Тогда линейный спрос можно представить как: Р = a – b(q 1 +q 2) = a – bq 1– bq 2 (1*) Обе фирмы имеют одинаковые условия по издержкам производства: ТCi = c* qi (2) где с - положительная константа. Таким образом, для каждого дуополиста предельные издержки равны средним: МCi = АCi = c (3) Цой Р. А. , РГЭУ (РИНХ) - 2014 11

Модель дуополии Курно Цой Р. А. , РГЭУ (РИНХ) - 2014 12

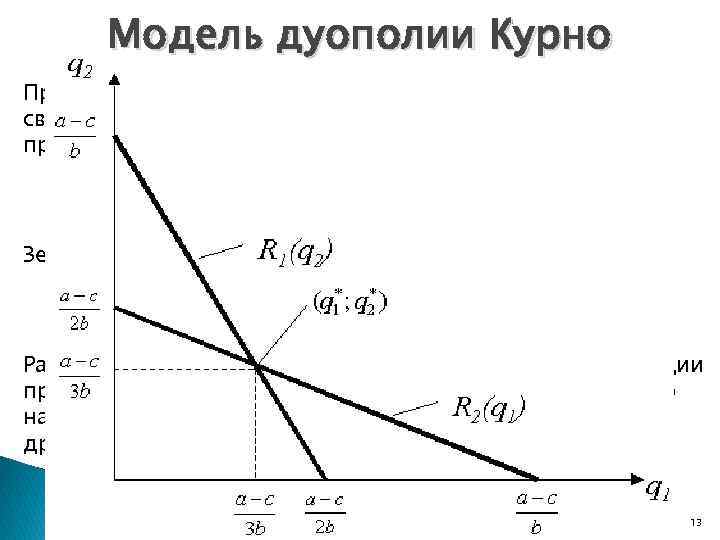Модель дуополии Курно Преобразовав это уравнение, получим функцию, связывающую максимизирующий прибыль уровень производства Фирмы 1 с объемом производства Фирмы 2: (7) Зеркально решаем проблему Фирмы 2: (7*) Равновесное решение, т. е. решение проблемы максимизации прибыли лежит на пересечении двух кривых реакции. Оно находится посредством подстановки одного уравнения в другое: (8) Цой Р. А. , РГЭУ (РИНХ) - 2014 13

Равновесие в модели дуополии Курно Для того чтобы определить равновесные объёмы выпуска обеих фирм, подставим выражение q 2 в уравнение (7) и наоборот и получим: q 1*= (a – c)/3 b (9) q 2*= (a – c)/3 b q 1*= q 2* (9*) Как видно из полученного уравнения и рисунка, равновесный совокупный объём выпуска обеих фирм (Q*), которые действуют независимо друг от друга покрывает лишь 2/3 рыночного спроса, равного Q = (a – c)/b: (10) Цой Р. А. , РГЭУ (РИНХ) - 2014 14

Равновесие в модели дуополии Курно При этом равновесная цена составит: (11) Каждый дуополист, при этом, сможет получить прибыль в размере: (12) Прибыль можно рассчитать из условия: πi = TRi – TCi = Pqi – cqi (13) подставив соответствующие выражения объёма выпуска каждой фирмы и цены. Цой Р. А. , РГЭУ (РИНХ) - 2014 15

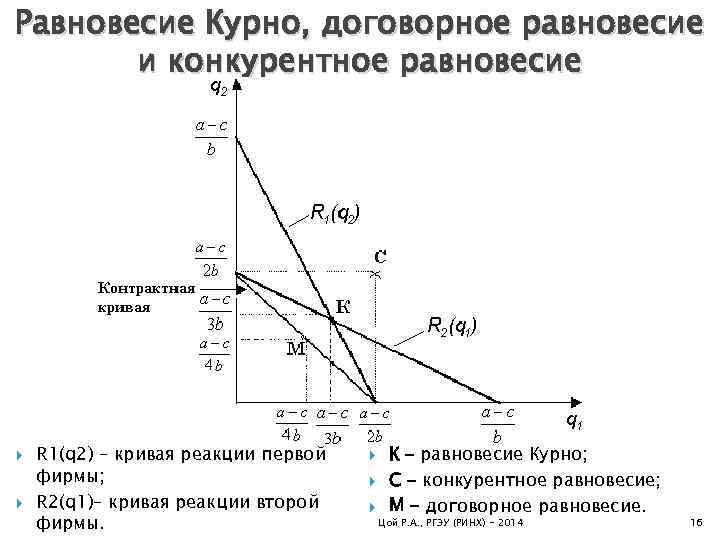Равновесие Курно, договорное равновесие и конкурентное равновесие R 1(q 2) – кривая реакции первой фирмы; R 2(q 1)– кривая реакции второй фирмы. К – равновесие Курно; С – конкурентное равновесие; М – договорное равновесие. Цой Р. А. , РГЭУ (РИНХ) - 2014 16

Договорное равновесие Цой Р. А. , РГЭУ (РИНХ) - 2014 17

Конкурентное равновесие Цой Р. А. , РГЭУ (РИНХ) - 2014 18

Соотношение прибылей < < Цой Р. А. , РГЭУ (РИНХ) - 2014 19

Характеристика отраслевого рынка с доминирующей фирмой 1. Издержки доминирующей фирмы на единицу продукции, как правило, значительно ниже, чем у фирм-конкурентов. Это возможно: а) если доминирующая фирма обладает более эффективной технологией или более качественными ресурсами (включая лучший менеджмент); б) если доминирующая фирма в большей степени, чем конкуренты способна усваивать и использовать накопленный опыт; в) если доминирующая фирма обладает преимуществами экономии на масштабах производства. 2. 3. Доминирующая фирма может выпускать продукт более высокого качества, чем аутсайдеры. Доминирующей фирмой может стать группа относительно небольших фирм, заключивших картельное соглашение между собой. Цой Р. А. , РГЭУ (РИНХ) - 2014 20

Модель «следовать за лидером» Штаккельберга Дуополист 1 Дуополист 2 1 Лидер Последователь 2 Последователь Лидер 3 Последователь 4 Лидер Тип взаимодействия Стабильный Модель Курно Ценовая война Цой Р. А. , РГЭУ (РИНХ) - 2014 21

Модель Штаккельберга «лидер-лидер» Цой Р. А. , РГЭУ (РИНХ) - 2014 22

Модель Штаккельберга «последователь-последователь» подставим в уравнение прибыли дуополиста 1 -лидера (7) функцию реагирования дуополиста 2 (25*): (26) (26*) Это и есть оптимальный выпуск последователя Штаккельберга. Таким образом, оптимальный выпуск последователя вдвое ниже оптимального выпуска лидера: Цой Р. А. , РГЭУ (РИНХ) - 2014 23

Модель Штаккельберга «следовать за лидером» Реакция лидера (27) Реакция последователя (27*) Равновесный объем выпуска Равновесная цена: (28) (29) Цой Р. А. , РГЭУ (РИНХ) - 2014 24

Модель Штаккельберга «следовать за лидером» Выпуск лидера в два раза превышает выпуск последователя. Можно определить как это отразится на прибыли дуополистов. (30) (30*) Очевидно, позиция лидера предпочтительней так как его прибыль в два раза превышает прибыль последователя. Цой Р. А. , РГЭУ (РИНХ) - 2014 25

Модель Бертрана в отличие от моделей Курно и Штаккельберга предполагают наличие ценового взаимодействия фирм на олигополистическом рынке. Таким образом конкуренция заключается в том, что каждая фирма устанавливает свою цену. Цой Р. А. , РГЭУ (РИНХ) - 2014 26

Условия модели Бертрана: 1) на рынке действуют две фирмы; 2) продукт производится однородный; 3) целью каждой фирмы является максимизация прибыли; 4) отсутствуют соглашения фирм друг с другом; 5) фирмы назначают цены одновременно так, что каждая не может прогнозировать реакцию конкурента на сделанный ею самой выбор. Цой Р. А. , РГЭУ (РИНХ) - 2014 27

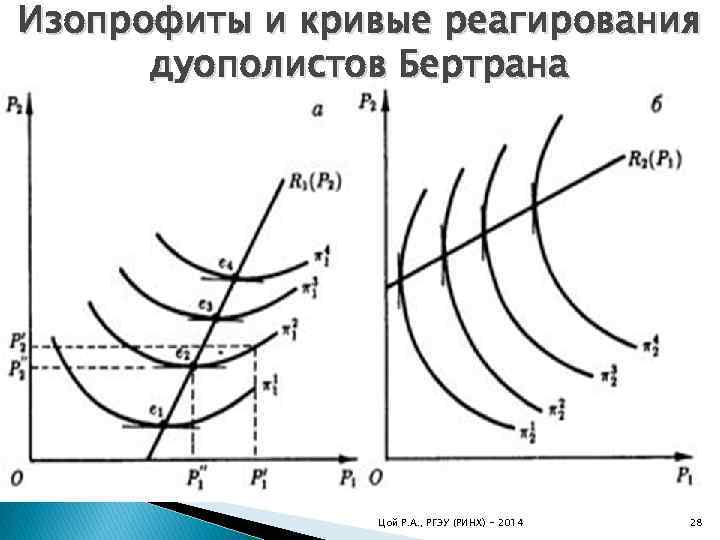Изопрофиты и кривые реагирования дуополистов Бертрана Цой Р. А. , РГЭУ (РИНХ) - 2014 28

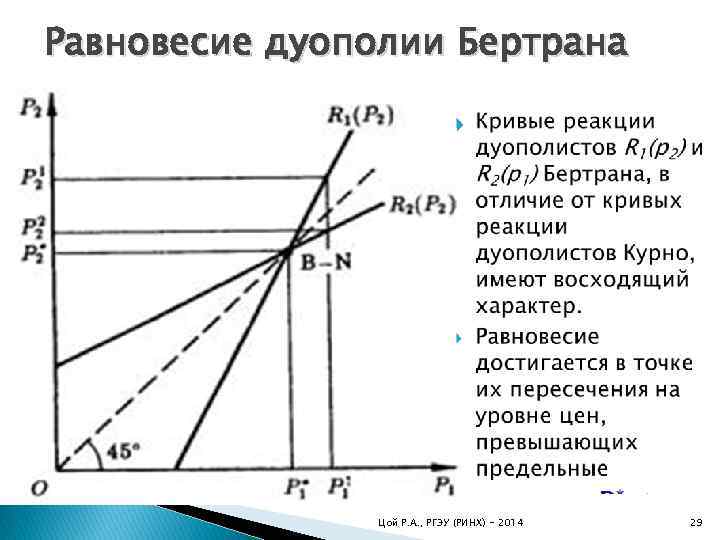Равновесие дуополии Бертрана Цой Р. А. , РГЭУ (РИНХ) - 2014 29

Модель Бертрана Стратегическое поведение фирм в данной модели можно назвать войной цен. Ценовая война – это цикл последовательных уменьшений цены соперничающими фирмами. на олигополистическом рынке Снижая цену ниже цены своего конкурента, каждый продавец стремиться захватить весь рынок. Но конкурент также отвечает понижением цены. Война цен продолжается до тех пор, пока цена не падает до уровня предельных и средних издержек – до конкурентного равновесия: p*=МС= АС = с (31) В условиях равновесия фирмы получают нулевую экономическую прибыль и делят рынок поровну, поскольку товар они продают по одинаковой цене. Цой Р. А. , РГЭУ (РИНХ) - 2014 30

Модель Бертрана Таким образом объем продаж в модели Бертрана является функцией от цены, поэтому функцию рыночного спроса следует представить в виде: Р = а – b. Q, где Q = q 1 + q 2 Тогда обратная функция спроса будет Q = q 1 + q 2 = (a/b) – (1/b)P (32) Две фирмы выбирают цены p 1 и p 2. Затраты фирм носят пропорциональный характер: ТC 1 = c×q 1 и ТC 2 = c×q 2 Цой Р. А. , РГЭУ (РИНХ) - 2014 31

Модель Бертрана Спрос на продукцию одного дуополиста формируется в зависимости от соотношения цен обоих дуополистов. Обозначив функцию спроса Q=D(p), формирование спроса отдельного дуополиста можно представить в трех вариантах: Цой Р. А. , РГЭУ (РИНХ) - 2014 32

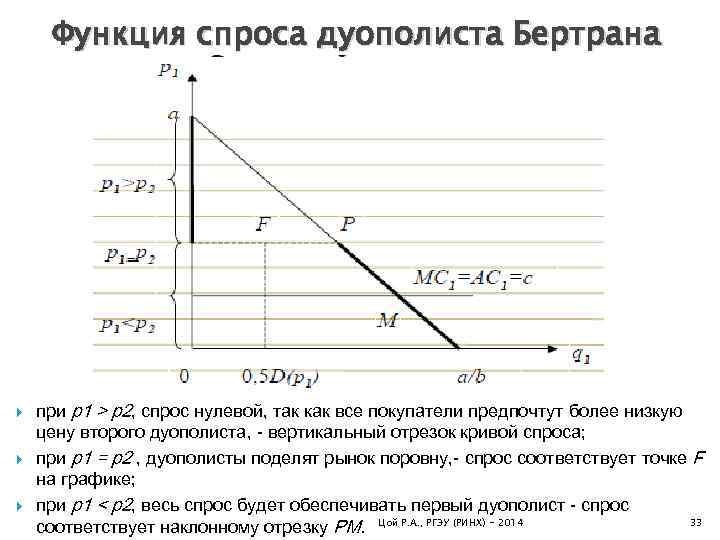Функция спроса дуополиста Бертрана при p 1 > p 2, спрос нулевой, так как все покупатели предпочтут более низкую цену второго дуополиста, - вертикальный отрезок кривой спроса; при p 1 = p 2 , дуополисты поделят рынок поровну, - спрос соответствует точке F на графике; при p 1 < p 2, весь спрос будет обеспечивать первый дуополист - спрос 33 соответствует наклонному отрезку PM. Цой Р. А. , РГЭУ (РИНХ) - 2014

Модель Бертрана Тогда, в рассматриваемой модели объем выпуска первого дуополиста может иметь следующие варианты: Цой Р. А. , РГЭУ (РИНХ) - 2014 34

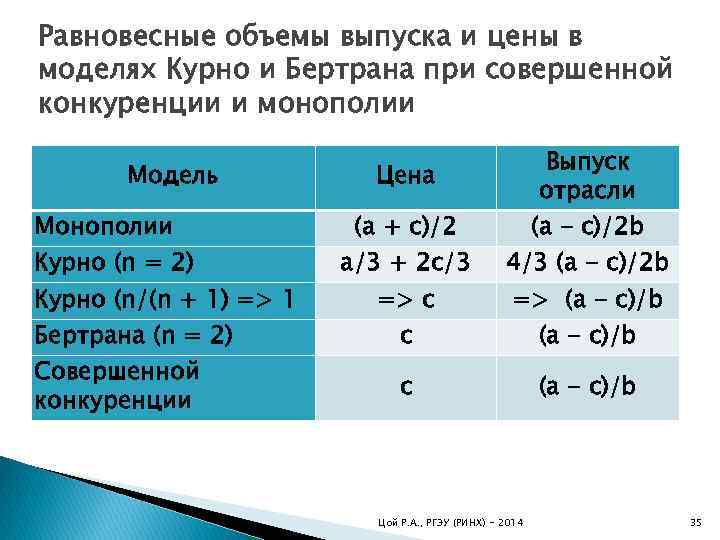Равновесные объемы выпуска и цены в моделях Курно и Бертрана при совершенной конкуренции и монополии Модель Монополии Курно (n = 2) Курно (n/(n + 1) => 1 Бертрана (n = 2) Совершенной конкуренции Выпуск отрасли Цена (a + c)/2 (a - c)/2 b a/3 + 2 c/3 4/3 (a - c)/2 b c (a - c)/b => c => (a - c)/b c Цой Р. А. , РГЭУ (РИНХ) - 2014 (a - c)/b 35

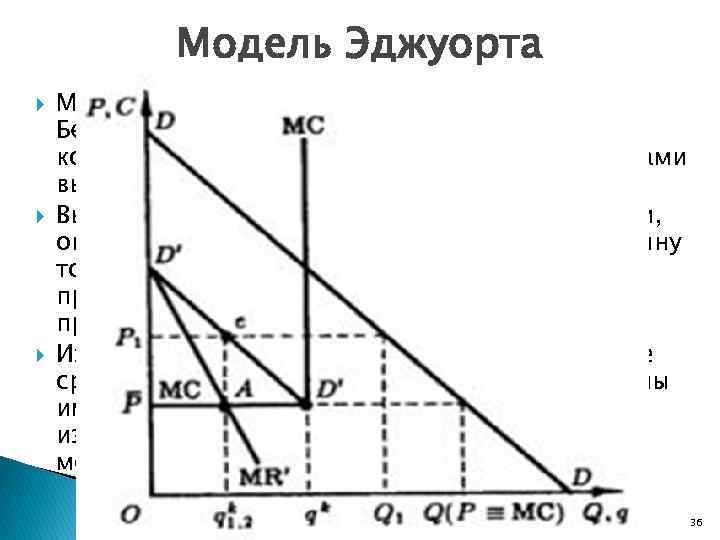Модель Эджуорта Модель Эджуорта является версией модели Бертрана, которая показывает модель ценовой конкуренции фирмы с ограниченными размерами выпуска. Выпуск каждой фирмы, действующей в отрасли, ограничен величиной qк, составляющей половину того объема выпуска отрасли, на который предъявляется спрос при цене, равной предельным издержкам. Из-за ограниченных размеров выпуска, кривые средних и предельных издержек каждой фирмы имеют вертикальный вид при qk: предельные издержки производства следующей единицы можно считать стремящимися к бесконечности. Цой Р. А. , РГЭУ (РИНХ) - 2014 36

Модель Эджуорта Цой Р. А. , РГЭУ (РИНХ) - 2014 37

Модель Эджуорта В ответ на это дуополист 2 повысит свою цену до уровня чуть ниже P 1, цены дуополиста 1, с тем чтобы привлечь к себе его покупателей. Однако из-за ограниченности своей производственной мощности дуополист 2 сможет покрыть спрос лишь в объеме Q 1 - q 1 = 2/3 Q 1 = Q 1(P = МС)/2. Продавая по чуть более низкой, чем у дуополиста 1, цене вдвое больше продукции, дуополист 2 получит, вероятно, и вдвое большую прибыль. Тогда дуополист 1 в свою очередь снизит цену до уровня чуть ниже, чем цена дуополиста 2. Словом, они попытаются опередить друга в снижении цен. Попытки заработать на снижении цены будут продолжаться, пока она не достигнет уровня P = MC + (P 1 - MC)(q 1/qk) (33) Цой Р. А. , РГЭУ (РИНХ) - 2014 38

Модель Эджуорта Дуополисты будут рассуждать примерно так: Если я снижу свою цену до Р, что чуть ниже цены соперника, я смогу продать максимально возможный для меня объем выпуска, qk. С другой стороны, если я увеличу свою цену до P 1, я смогу продать лишь q 1 единиц продукции. При какой цене Р моя прибыль окажется точно такой же, как и при цене P 1? Ответ на этот вопрос можно получить, решив относительно Р уравнение (P 1 - MC)qi = (P - MC)q (34) Решение: P = MC + (P 1 - MC)(q 1/qk) Цой Р. А. , РГЭУ (РИНХ) - 2014 (33) 39

Модель Эджуорта Но как только цена действительно упадет до Р, выгодным для любого дуополиста вновь становится повышение цены до P 1, и весь ценовой цикл повторится. Таким образом, модель Эджуорта не предрекает никакого статичного равновесия. Скорее это некая "ценовая ловушка", попав в которую дуополисты втягиваются в нескончаемую ценовую войну, в которой падения цен чередуются с их всплесками. Цой Р. А. , РГЭУ (РИНХ) - 2014 40

КОЛИЧЕСТВЕННАЯ ИЛИ ЦЕНОВАЯ ОЛИГОПОЛИЯ? Модель ценовой конкуренции более реалистично представляет поведение олигополистов, чем модель количественной олигополии. Причиной тому может быть большая легкость манипулирования ценами, чем объемами выпуска. Для того чтобы варьировать объемы выпуска, могут понадобиться и дополнительные инвестиции в производственные мощности, и время. Варьировать ценами проще и "дешевле", хотя и здесь существуют известные ограничения (уже заключенные договора на поставку продукции и покупку сырья и материалов, расходы на переиздание каталогов и прейскурантов и т. п. ). Так что на деле модели количественной и ценовой олигополии не противостоят, а скорее дополняют друга, образуя достаточно широкий инструментарий для анализа олигопольных рынков. Цой Р. А. , РГЭУ (РИНХ) - 2014 41

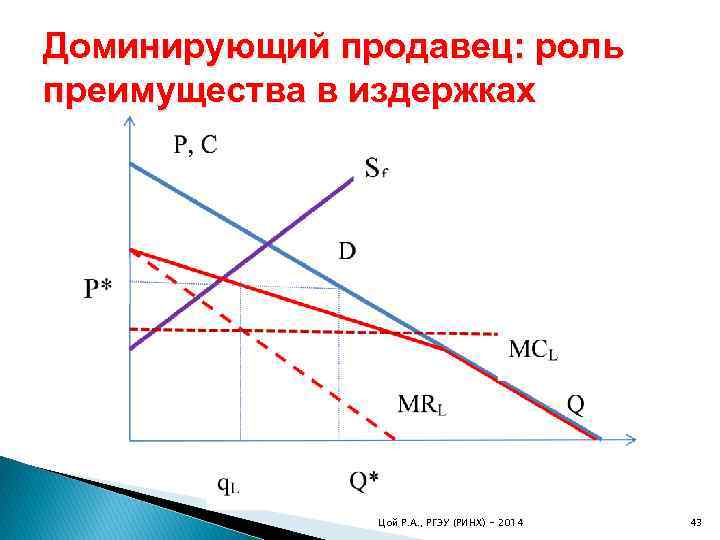
Доминирующий продавец: роль преимущества в издержках Предпосылки: Ø много мелких конкурентов; Ø свободный вход и выход; Ø для покупателя продукт однороден; Ø Ø Ø предложение «конкурентного окружения» - как в модели совершенной конкуренции; price-takers, условие максимизации прибыли MC=P; преимущество доминирующего продавца в издержках; Ø остаточный спрос; Ø максимизация прибыли по «остаточному спросу» ; Цой Р. А. , РГЭУ (РИНХ) - 2014 42

Доминирующий продавец: роль преимущества в издержках Цой Р. А. , РГЭУ (РИНХ) - 2014 43

Доминирующий продавец: роль преимущества в издержках Ø при снижении издержек лидера его доля на рынке вырастет; Ø при снижении издержек «конкурентного окружения» доля лидера снизится; Цой Р. А. , РГЭУ (РИНХ) - 2014 44

Доминирующий продавец: роль преимущества в издержках Интерпретация? Преимущество либо в издержках, либо в качестве Все ли так безоблачно? Издержки «конкурентного окружения» случайно не зависят от лидера? Цой Р. А. , РГЭУ (РИНХ) - 2014 45

Методы теории игр для анализа поведения олигополии Теория игр представляет собой науку, которая исследует математическими методами поведение участников в вероятностных ситуациях связанных с принятием решений. Простейшим изображения игры является матрица результатов. Матрица результатов представляет собой двухстороннюю таблицу, образованную множеством квадратов, каждый из которых представляет результат стратегического взаимодействия обоих участников. Цой Р. А. , РГЭУ (РИНХ) - 2014 46

Представление игр Игры представляют собой строго определённые логикоматематические объекты. Игра образуется игроками, набором стратегий для каждого игрока и указания выигрышей, или платежей, игроков для каждой комбинации стратегий. Характеризующие признаки игры: наличие нескольких участников; неопределенность поведения участников, связанная с наличием у каждого из них нескольких вариантов действий; различие (несовпадение) интересов участников; взаимосвязанность поведения участников, поскольку результат, получаемый каждым из них, зависит от поведения всех участников; наличие правил поведения, известных всем участникам. Цой Р. А. , РГЭУ (РИНХ) - 2014 47

Кооперативные и некооперативные Игра называется кооперативной, или коалиционной, если игроки могут объединяться в группы, взяв на себя некоторые обязательства перед другими игроками и координируя свои действия. Этим она отличается от некооперативных игр, в которых каждый обязан играть за себя. Цой Р. А. , РГЭУ (РИНХ) - 2014 48

Игра с нулевой суммой - особая разновидность игр с постоянной суммой, то есть таких, где игроки не могут увеличить или уменьшить имеющиеся ресурсы, или фонд игры. В этом случае сумма всех выигрышей равна сумме всех проигрышей при любом ходе. Примерами таких игр может служить покер, где один выигрывает все ставки других; реверси, где захватываются фишки противника; либо банальное воровство. Цой Р. А. , РГЭУ (РИНХ) - 2014 49

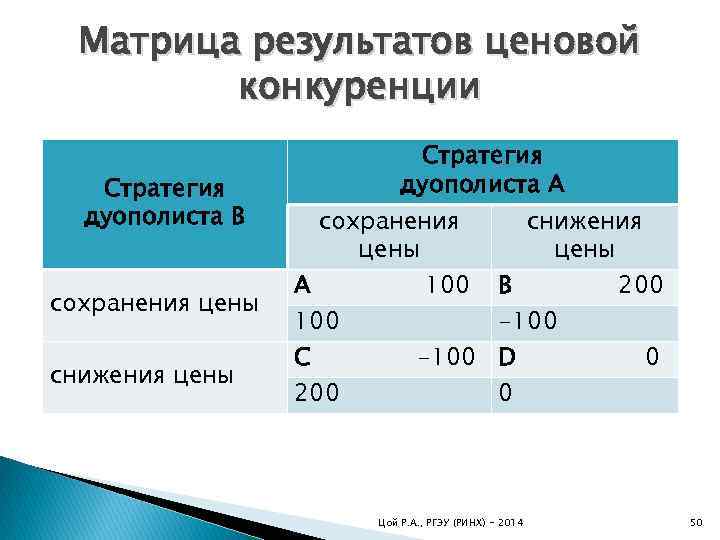Матрица результатов ценовой конкуренции Стратегия дуополиста В сохранения цены снижения цены Стратегия дуополиста А сохранения цены A 100 C 200 100 снижения цены B -100 D 0 Цой Р. А. , РГЭУ (РИНХ) - 2014 200 0 50

Матрица результатов ценовой конкуренции Если фирмы будут конкурировать, то положение равновесия будет достигнуто в квадрате D, где прибыль каждого будет равна нулю. Такое решение получило название равновесия Нэша. Равновесием Нэша называется такое решение игры, от которого нет оснований отказываться ни одному из игроков в одиночку. В случае конкуренции рассмотренный случай соответствует уже известной нам модели Бертрана. Если продавцы договариваются между собой, т. е. образуют картель, то этот сговор приносит им максимальную прибыль, которая представлена в квадрате А. Цой Р. А. , РГЭУ (РИНХ) - 2014 51

Дилемма заключенного Два заключенных поставлены перед дилеммой: Они не сознаются в преступлении и тогда Поведение первого Поведение получают по два года заключения каждый, заключенного второго заключенного либо сознается не сознаваться кто-то один, сознаться за который признание отправляется в тюрьму на один год, A 2 1 год но другой получает 5 лет. года B не сознаваться 2 года 5 лет Если они сознаются оба, то получают оба по 3 C 5 лет D 3 года. сознаться 1 год 3 года Вся проблема заключается в том, что каждый поставлен перед своей дилеммой отдельно. Цой Р. А. , РГЭУ (РИНХ) - 2014 52

Дилемма заключенного Наиболее вероятное решение в этом случае может быть достигнуто в квадрате D, когда каждый получит по 3 года. Но этот результат вероятен, если они не могут между собой договориться. Если сговор возможен, то они получают по 2 года. По аналогии с продавцами, ситуация демонстрирует желание продавцов вступать в сговор на рынке для достижения наиболее благоприятного для каждого из них результата, вместо того чтобы конкурировать и снижать свои прибыли до минимума (квадрат D). Цой Р. А. , РГЭУ (РИНХ) - 2014 53