Теория определителей Понятие определителя вводится лишь для квадратных

Теория определителей. Понятие определителя вводится лишь для квадратных матриц. Определитель- это число. Обозначения:

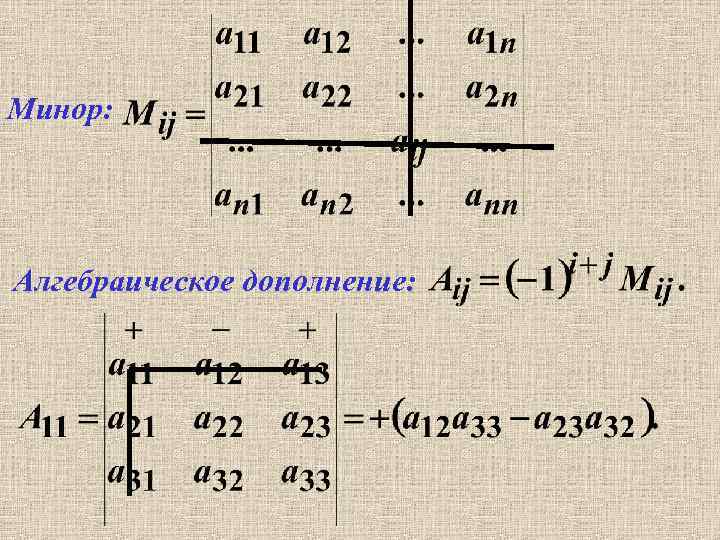Минор: Алгебраическое дополнение:

Определитель: разложение определителя по 1 -й строке

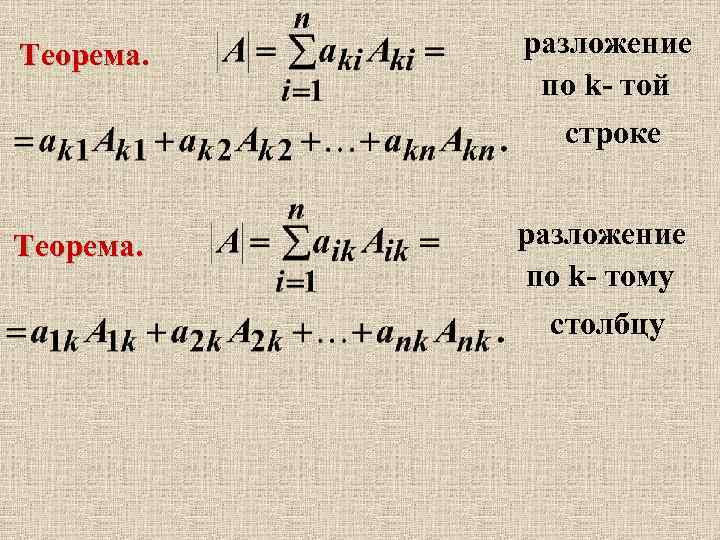Теорема. разложение по k- той строке Теорема. разложение по k- тому столбцу

Свойства определителей. 1. Если в определителе есть нулевая строка (столбец), то он равен 0. 2. При перестановке двух строк (столбцов) определитель меняет знак. Доказательство.

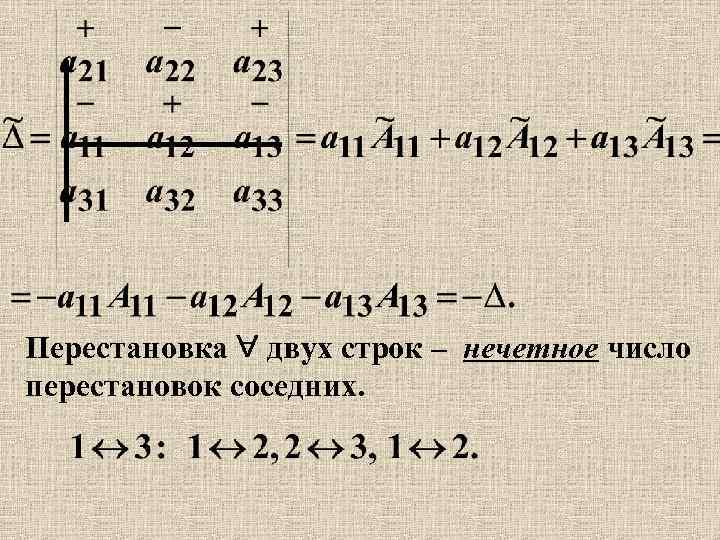Перестановка двух строк – нечетное число перестановок соседних.

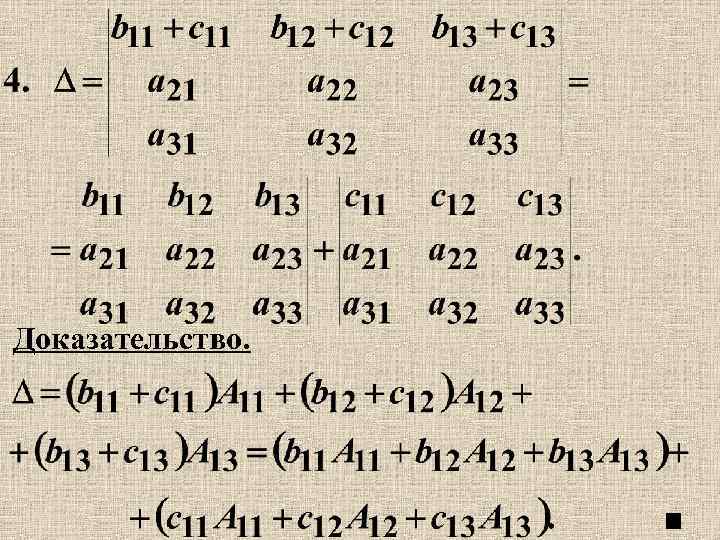3. Определитель с двумя одинаковыми строками равен 0. Доказательство.

Доказательство.

Доказательство.

7. Если одна из строк определителя есть линейная комбинация других строк, то определитель равен нулю. 8. Если к строке определителя прибавить линейную комбинацию других его строк, то определитель не изменится.

9. Сумма произведений элементов какй-либо строки на соответствующие алгебраические дополнения другой строки равна нулю. Доказательство.

Доказательство проводится разложением определителя и алгебраических дополнений по первому столбцу. Вычисление определителей методом элементарных преобразований (метод Гаусса).

ОБРАТНАЯ МАТРИЦА Определение 1. Квадратная матрица А называется невырожденной, если |А| 0 , в противном случае матрица называется вырожденной (|А|=0 ). Определение 2. Квадратная матрица B называется обратной по отношению к матрице А того же порядка, если АB=BA=I. Обратная матрица обозначается символом

Определение 3. Матрица А* называется присоединенной к матрице А, если в ее к-ой строке стоят алгебраические дополнения элементов к-ого столбца матрицы А.

Теорема 1. Для того чтобы существовала необходимо и достаточно, чтобы матрица была невырожденной. Доказательство. Необходимость Достаточность

Теорема 2. Если то она единственна. Свойства обратной матрицы Доказательство.

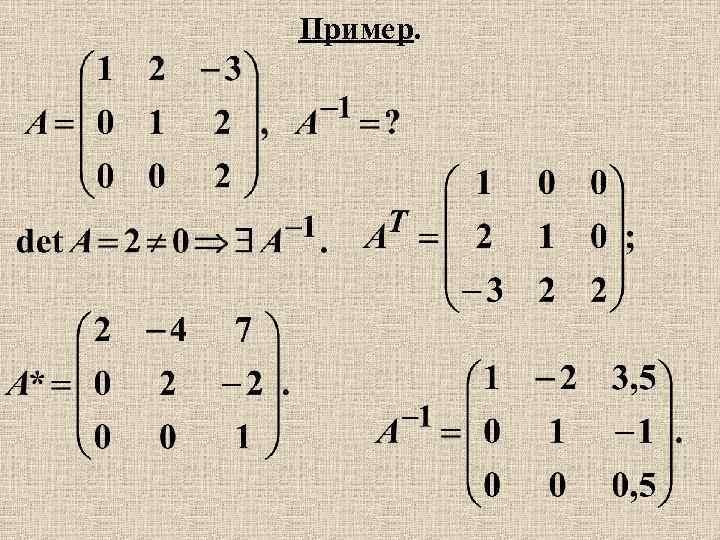Пример.

Формулы Крамера для решения системы линейных алгебраических уравнений (СЛАУ) с невырожденной квадратной матрицей.

- алгебраическое дополнение элемента в матрице - определитель, который получится, если в матрице A заменить к-ый столбец столбцом правых частей B. формулы Крамера

Теорема. СЛАУ с невырожденной квадратной матрицей имеет и притом единственное решение, определяемое по формулам Крамера. Итак, если 0, то СЛАУ с квадратной матрицей имеет единственное решение. Если =0 и хотя бы один k 0, то СЛАУ с квадратной матрицей не имеет ни одного решения- несовместна. Если =0 и все k=0, то СЛАУ с квадратной матрицей имеет бесконечно много решений.

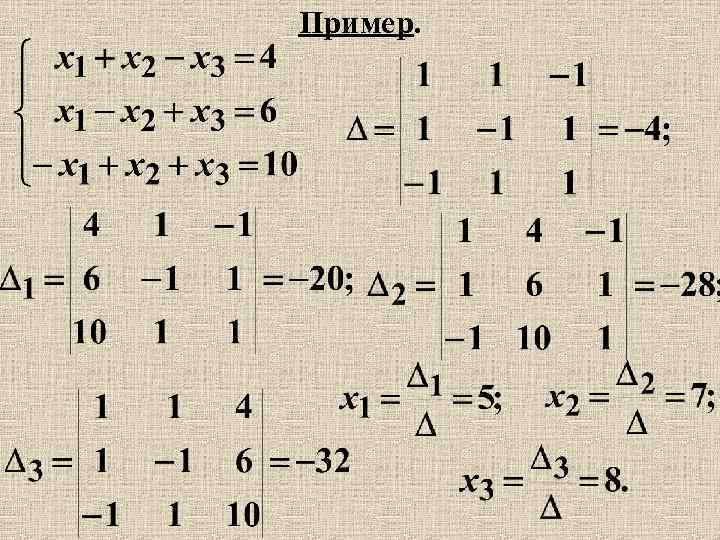Пример.