Теория напряженного состояния Плоское напряженное состояние Плоское

Теория напряженного состояния Плоское напряженное состояние

Плоское напряженное состояние Взаимодействие между частями элемента конструкции характеризуется величинами нормальных и касательных напряжений в каждой точке элемента Совокупность нормальных и касательных напряжений, действующих по всем площадкам, проходящим через рассматриваемую точку, называется напряженным состоянием в рассматриваемой точке Различают следующие виды напряженного состояния: Пространственное (трехосное) напряженное состояние Плоское (двухосное) напряженное состояние Линейное (одноосное) напряженное состояние

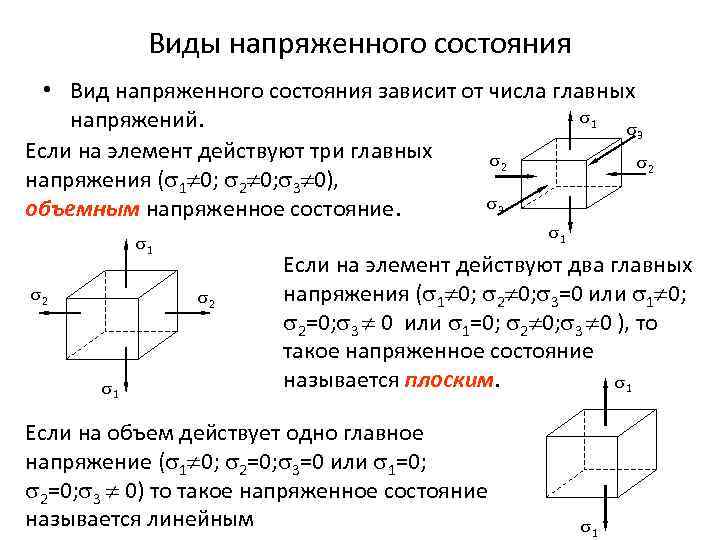Виды напряженного состояния • Вид напряженного состояния зависит от числа главных 1 напряжений. 3 Если на элемент действуют три главных 2 2 напряжения ( 1 0; 2 0; 3 0), 3 объемным напряженное состояние. 1 1 2 2 1 Если на элемент действуют два главных напряжения ( 1 0; 2 0; 3=0 или 1 0; 2=0; 3 0 или 1=0; 2 0; 3 0 ), то такое напряженное состояние называется плоским. 1 Если на объем действует одно главное напряжение ( 1 0; 2=0; 3=0 или 1=0; 2=0; 3 0) то такое напряженное состояние называется линейным 1

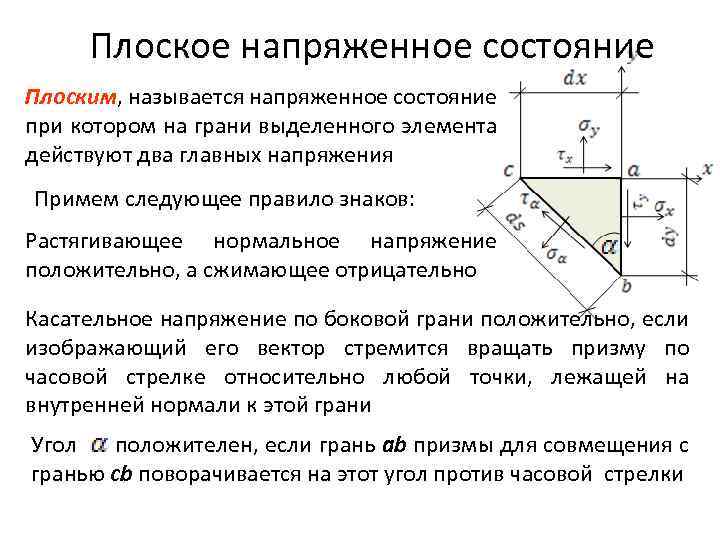Плоское напряженное состояние Плоским, называется напряженное состояние при котором на грани выделенного элемента действуют два главных напряжения Примем следующее правило знаков: Растягивающее нормальное напряжение положительно, а сжимающее отрицательно Касательное напряжение по боковой грани положительно, если изображающий его вектор стремится вращать призму по часовой стрелке относительно любой точки, лежащей на внутренней нормали к этой грани Угол положителен, если грань ab призмы для совмещения с гранью cb поворачивается на этот угол против часовой стрелки

Плоское напряженное состояние Умножив каждое из напряжений на площадь грани получим систему сосредоточенных сил (1) Эти силы должны удовлетворять всем условиям (уравнениям) равновесия (2) (3) (4) (5) Эта связь называется законом парности касательных напряжений Следовательно, касательные напряжения по двум взаимно перпендикулярным площадкам равны по абсолютной величине и обратные по знаку

Плоское напряженное состояние Подставим в уравнения (2) и (3) выражения сил из равенств (1) Сократим эти уравнения на ds dz, учитывая при этом, что Теперь заменим (6) (7) Формулы (6) и (7) позволяют определять значения нормальных и касательных напряжений в любых площадках, проходящих через данную точку, если известны напряжения в любых двух проходящих через нее взаимно перпендикулярных площадках

Плоское напряженное состояние Определим по формуле (6) сумму нормальных напряжений в двух взаимно перпендикулярных площадках, для одной из которых угол Таким образом т. е. сумма величин нормальных напряжений в перпендикулярных площадках есть величина постоянная (8) двух взаимно Следовательно, если в одной из таких площадок нормальные напряжения имеют максимальное значение, то в другой они имеют минимальное значение

Вопросы для самоконтроля • 1. Какое напряженное состояние называется пространственным (трехосным)? • 2. Какое напряженное состояние называется плоским (двухосным)? • 3. Какое напряженное состояние называется линейным (одноосным)? • 4. Вывод формул, позволяющих определять значения нормальных и касательных напряжений в любых площадках, проходящих через данную точку, если известны напряжения в любых двух проходящих через нее взаимно перпендикулярных площадках

Вопросы для самоконтроля • 5. Каково правило знаков для нормальных и касательных напряжений? • 6. Доказать закон парности касательных напряжений. • 7. Чему равна сумма нормальных напряжений на любых двух взаимно перпендикулярных площадках? • 8. В чем сущность принципа наложения напряжений?