 Теория напряжения Лекция № 2
Теория напряжения Лекция № 2
 • Тензор упругих напряжений • Рассмотрены простые случаи деформации, и в связи с этим нормальные и касательные напряжения, образующие общее напряжение, ориентированное под произвольным углом к сечению тела. В общем случае вектор напряжения зависит от ориентировки площадки. • Для составления широкого представления о напряжении рассмотрим точку М(х, у, z) и построим площадку S, включающую данную точку. Ориентировку площадки определим нормалью n к ней. Пусть на эту площадку со стороны той части среды, куда направлена нормаль, действует сила F. Тогда вектор напряжения на площадке определяется формулой и индексом n у вектора • отмечается ориентировка площадки.
• Тензор упругих напряжений • Рассмотрены простые случаи деформации, и в связи с этим нормальные и касательные напряжения, образующие общее напряжение, ориентированное под произвольным углом к сечению тела. В общем случае вектор напряжения зависит от ориентировки площадки. • Для составления широкого представления о напряжении рассмотрим точку М(х, у, z) и построим площадку S, включающую данную точку. Ориентировку площадки определим нормалью n к ней. Пусть на эту площадку со стороны той части среды, куда направлена нормаль, действует сила F. Тогда вектор напряжения на площадке определяется формулой и индексом n у вектора • отмечается ориентировка площадки.
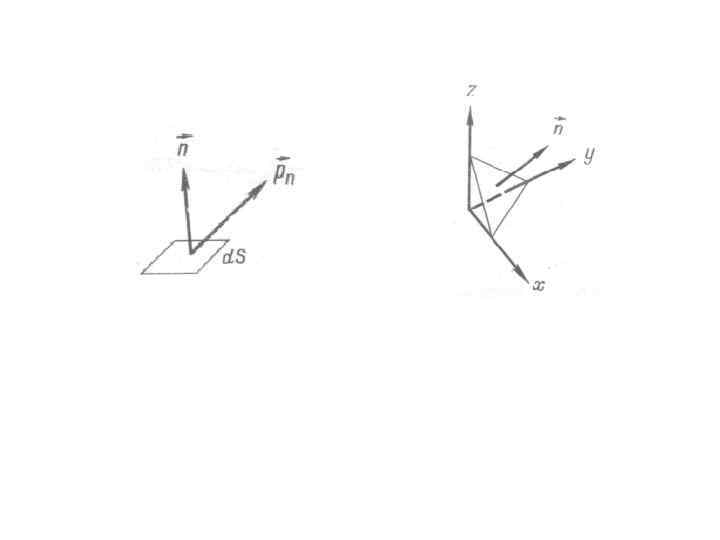
 • Для данной точки можно построить бесконечное количество площадки с различной ориентировкой. • Но для полного представления напряжения в этой точке достаточно знать три вектора напряжения по трем взаимно перпендикулярным плоскостям. Поэтому выберем три взаимно перпендикулярные площадки, нормали которых совпадают с координатными осями ox, oy, oz. • Тогда векторы напряжения определяются индексами: • Каждый из них определяются тремя проекциями по координатным осям. В этом случае на каждую составляющую приписываются по два индекса, первый- указывает ориентировку площадки, второй – направление составляющих.
• Для данной точки можно построить бесконечное количество площадки с различной ориентировкой. • Но для полного представления напряжения в этой точке достаточно знать три вектора напряжения по трем взаимно перпендикулярным плоскостям. Поэтому выберем три взаимно перпендикулярные площадки, нормали которых совпадают с координатными осями ox, oy, oz. • Тогда векторы напряжения определяются индексами: • Каждый из них определяются тремя проекциями по координатным осям. В этом случае на каждую составляющую приписываются по два индекса, первый- указывает ориентировку площадки, второй – направление составляющих.
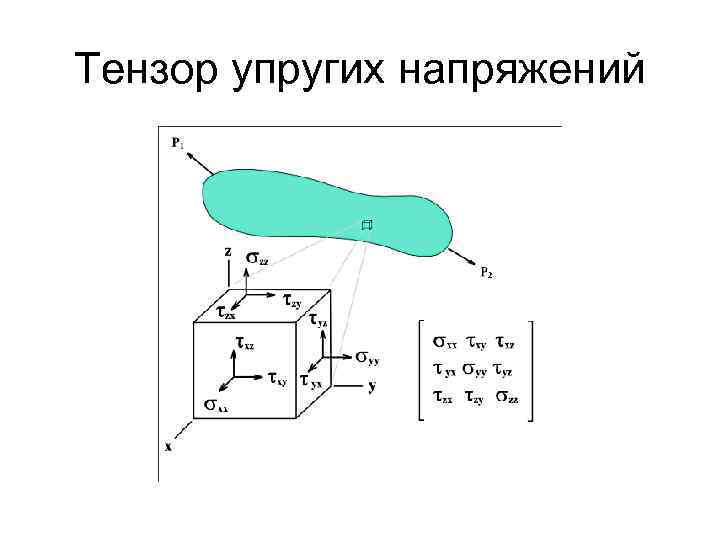
 • Итак, три вектора с девятью составляющими образуют тензор упругих напряжений: • В каждой горизонтальной строке собраны составляющие одного вектора. .
• Итак, три вектора с девятью составляющими образуют тензор упругих напряжений: • В каждой горизонтальной строке собраны составляющие одного вектора. .
 • Три составляющие Рхх, Руу, Рzz, расположенные по главной диагонали матрицы, соответствуют нормальным, а остальные касательным напряжениям на площадках. • Следовательно, нормальные напряжения вызывают – растяжение и сжатие, касательные напряжения – сдвиговую деформацию. • К тому тензор симметричен.
• Три составляющие Рхх, Руу, Рzz, расположенные по главной диагонали матрицы, соответствуют нормальным, а остальные касательным напряжениям на площадках. • Следовательно, нормальные напряжения вызывают – растяжение и сжатие, касательные напряжения – сдвиговую деформацию. • К тому тензор симметричен.
 • Тензоры можно складывать и вычитать, при этом суммой двух тензоров является тензор, компоненты которого представляют собой сумму соответствующих компонентов слагаемых тензоров. • При умножении тензора на скалярную величину получится новый тензор, все компоненты которого в n раз больше компонентов исходного тензора.
• Тензоры можно складывать и вычитать, при этом суммой двух тензоров является тензор, компоненты которого представляют собой сумму соответствующих компонентов слагаемых тензоров. • При умножении тензора на скалярную величину получится новый тензор, все компоненты которого в n раз больше компонентов исходного тензора.
 Тензор упругих напряжений
Тензор упругих напряжений
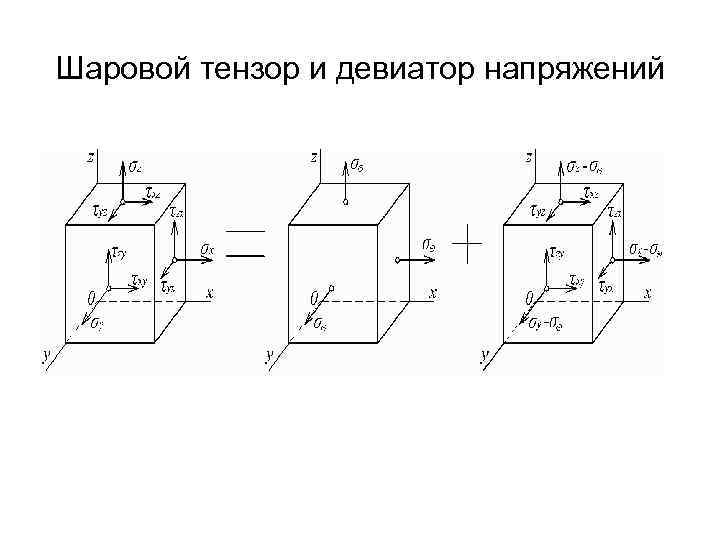
 • Рассмотрим напряженное состояние, при котором на трех взаимно перпендикулярных площадках действуют только три одинаковых главных напряжения: • Такое напряженное состояние описывается тензором, котoрый называется шаровым тензором напряжений:
• Рассмотрим напряженное состояние, при котором на трех взаимно перпендикулярных площадках действуют только три одинаковых главных напряжения: • Такое напряженное состояние описывается тензором, котoрый называется шаровым тензором напряжений:
 • При вычитании шарового тензора из тензора напряжений получается новый тензор, который называется девиатором напряжений: • Таким образом, тензор напряжений в любой точке тела может быть представлен в виде суммы шарового тензора и девиатора напряжений:
• При вычитании шарового тензора из тензора напряжений получается новый тензор, который называется девиатором напряжений: • Таким образом, тензор напряжений в любой точке тела может быть представлен в виде суммы шарового тензора и девиатора напряжений:
 • Шаровой тензор выделяет из напряженного состояния равномерное всестороннее растяжение (сжатие), при котором изменяется только объем данного элемента без изменения его формы. • Девиатор напряжений характеризует состояние сдвига, при котором изменяется форма элемента без изменения его объема.
• Шаровой тензор выделяет из напряженного состояния равномерное всестороннее растяжение (сжатие), при котором изменяется только объем данного элемента без изменения его формы. • Девиатор напряжений характеризует состояние сдвига, при котором изменяется форма элемента без изменения его объема.
 Шаровой тензор и девиатор напряжений
Шаровой тензор и девиатор напряжений
 Преобразование компонент напряжения к новым осям координат. • При рассмотрении напряжения, приложенного к площадке с нормалью , и определении компонент этого напряжения было отмечено, что система координат ориентируется нами произвольно. • Если расположить систему координат так, чтобы одна из ее осей была параллельной нормали к площадке, то в этой системе координат изучаемое напряжение определилось бы только тремя компонентами. • Рассмотрим общие закономерности приведения компонент напряжений к новым осям координат.
Преобразование компонент напряжения к новым осям координат. • При рассмотрении напряжения, приложенного к площадке с нормалью , и определении компонент этого напряжения было отмечено, что система координат ориентируется нами произвольно. • Если расположить систему координат так, чтобы одна из ее осей была параллельной нормали к площадке, то в этой системе координат изучаемое напряжение определилось бы только тремя компонентами. • Рассмотрим общие закономерности приведения компонент напряжений к новым осям координат.
 • Введем некоторые обозначения: • тогда модули этих векторных величин определяются следующими выражениями: • (1) • где , , направляющие косинусы. и т. д. –
• Введем некоторые обозначения: • тогда модули этих векторных величин определяются следующими выражениями: • (1) • где , , направляющие косинусы. и т. д. –
 • Отметим, что они связывают напряжение на некоторой площадке с его компонентами по осям любой произвольно выбранной ортогональной системы координат. • При переходе к другой системе координат изменяются значения, как компонент, так и направляющих косинусов. • Зная компоненты напряжения, по осям первоначально выбранной системы и т. д. , определим компоненты в новой системе координат и т. д. (рисунок )
• Отметим, что они связывают напряжение на некоторой площадке с его компонентами по осям любой произвольно выбранной ортогональной системы координат. • При переходе к другой системе координат изменяются значения, как компонент, так и направляющих косинусов. • Зная компоненты напряжения, по осям первоначально выбранной системы и т. д. , определим компоненты в новой системе координат и т. д. (рисунок )
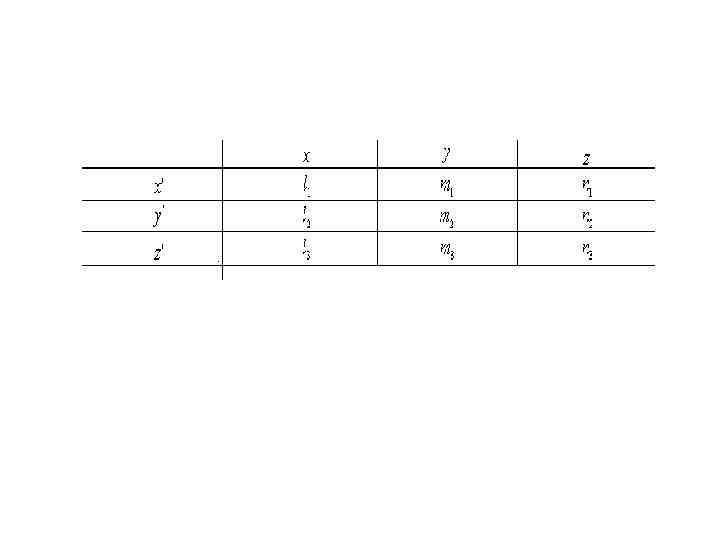
 • Новую систему координат со старой системой свяжем направляющими косинусами углов между первоначальными и новыми. • Определим проекции на первоначальные координатные оси напряжений, приложенных к площадкам, совпадающим с координатными плоскостями новой координатной системы. • Каждую такую площадку мы можем рассматривать как произвольно расположенную, с нормалью, заданной своими направляющими косинусами, и применить для определения искомых проекций формулы (1).
• Новую систему координат со старой системой свяжем направляющими косинусами углов между первоначальными и новыми. • Определим проекции на первоначальные координатные оси напряжений, приложенных к площадкам, совпадающим с координатными плоскостями новой координатной системы. • Каждую такую площадку мы можем рассматривать как произвольно расположенную, с нормалью, заданной своими направляющими косинусами, и применить для определения искомых проекций формулы (1).
 • Тогда для компонент напряжений на площадке, нормалью к которой является новая ось (заштрихованная площадка на рисунке), получим(2):
• Тогда для компонент напряжений на площадке, нормалью к которой является новая ось (заштрихованная площадка на рисунке), получим(2):
 • Чтобы определить проекции этих напряжений на новые оси, воспользуемся теоремой о том, что проекция вектора на направление равна сумме проекций его компонент на то же направление. • В соответствии с этой теоремой компонента по новой оси может быть получена путем суммирования трех компонент по первоначальным осям напряжения, приложенного к площадке с нормалью , предварительно умноженных на направляющие косинусы
• Чтобы определить проекции этих напряжений на новые оси, воспользуемся теоремой о том, что проекция вектора на направление равна сумме проекций его компонент на то же направление. • В соответствии с этой теоремой компонента по новой оси может быть получена путем суммирования трех компонент по первоначальным осям напряжения, приложенного к площадке с нормалью , предварительно умноженных на направляющие косинусы
 • Подстановка в правую часть первого уравнения системы (4) проекций на старые оси напряжения, приложенного к площадкам с нормалью , по уравнениям (2) позволяет, используя выше доказанное равенство касательных компонент и т. д. , записать в окончательной форме выражения для первой нормальной компоненты напряжения в новых осях координат
• Подстановка в правую часть первого уравнения системы (4) проекций на старые оси напряжения, приложенного к площадкам с нормалью , по уравнениям (2) позволяет, используя выше доказанное равенство касательных компонент и т. д. , записать в окончательной форме выражения для первой нормальной компоненты напряжения в новых осях координат
 • Второе и третье уравнения системы (4) после подстановки в них выражений (2) позволяют определить две касательные компоненты напряжений в новых осях
• Второе и третье уравнения системы (4) после подстановки в них выражений (2) позволяют определить две касательные компоненты напряжений в новых осях
 • Остальные компоненты напряжений в новых координатных осях находится аналогично. • Поэтому компоненты напряжения в осях х', у', z': σх′, σу′, . . . связаны с компонентами напряжения в осях х, у, z соотношениями:
• Остальные компоненты напряжений в новых координатных осях находится аналогично. • Поэтому компоненты напряжения в осях х', у', z': σх′, σу′, . . . связаны с компонентами напряжения в осях х, у, z соотношениями:
 • Сложим нормальные компоненты в новых координатах: • Известно, что • Следовательно, • т. е. сумма нормальных компонент напряжений не меняется при изменении осей координат.
• Сложим нормальные компоненты в новых координатах: • Известно, что • Следовательно, • т. е. сумма нормальных компонент напряжений не меняется при изменении осей координат.


