Теория множеств

Теория множеств N – множество всех натуральных чисел. N = {0, 1, 2, 3, …} N 1 - множество всех натуральных чисел не превосходящих 100 R - множество всех действительных чисел A 1 - множество студентов группы Ф 8300 А - множество групп в НФ ТПУ Подмножества: Ø – пустое множество Ø U – универсальное множество Способы задания множеств 1) Перечисление элементов 2) Характеристический предикат 3) Порождающая процедура

Алгебра множеств U={0, 1, 2, 3, 4, 5, 6, 7, 8, 9} A={0, 1, 3, 4, 6, 7, 8} B={1, 2, 3, 5, 8} 1. Включение множеств 2. Дополнение множества 6. Кольцевая сумма U Круги Эйлера, A U диаграммы Венна {2, 5, 9} B A U B A 3. Пересечение множеств 4. Объединение множеств 5. Разность U B B A ={1, 3, 8} ={0, 1, 2, 3, 4, 5, 6, 7, 8}

Свойства операций над множествами. 1. Идемпотентность 2. Коммутативность 3. Ассоциативность 4. Дистрибутивность 5. Поглощение 6. Инволютивность 7. Законы де Моргана Метод взаимного включения U 1) B A 2) 1) 2)

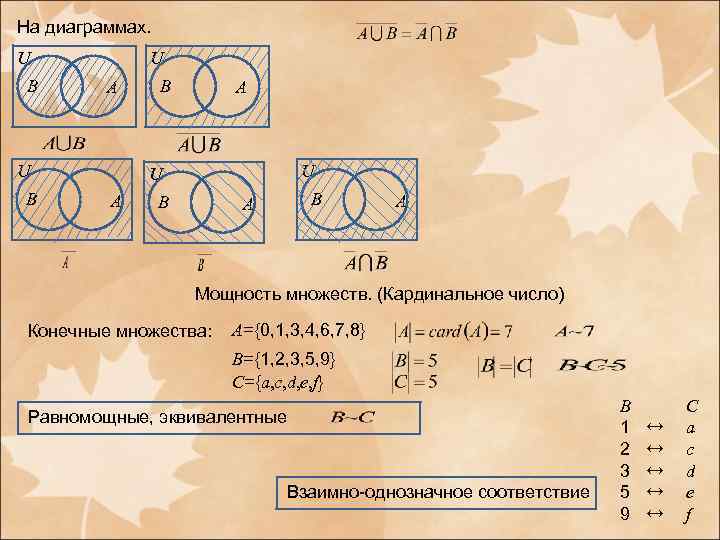
На диаграммах. U U B A B A Мощность множеств. (Кардинальное число) Конечные множества: A={0, 1, 3, 4, 6, 7, 8} B={1, 2, 3, 5, 9} C={a, c, d, e, f} B C Равномощные, эквивалентные ↔ 1 a 2 ↔ c 3 ↔ d Взаимно-однозначное соответствие 5 ↔ e 9 ↔ f

Бесконечные множества N – натуральный ряд чисел {0, 1, 2, 3, … } Счетные множества 6 4 2 0 1 3 5 z>0 -z<0 -3 -2 -1 0 1 2 3 Теорема. Множество всех действительных чисел отрезка несчетно. континуум континуальное O 0 1 a b 0 1

- упорядоченная пара (кортеж длины 2) (1, 2) 2 (2, 1) 1 - декартово (прямое) произведение 1 2 - декартова степень n – местное отношение (предикат) бинарное отношение (соответствие)

A – область отправления B – область прибытия - область определения - область значений Представление соответствий 1. Диаграмма 2. Матрица 2 2 3 4 5 6 7 8 4 2 5 3 6 4 7 5 8 6 2 3 4 5 6 7 8 7 8

Операции над бинарными отношениями 1. Объединение 2. Пересечение 3. Дополнение 4. Обратное отношение

6. Композиция соответствий a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3

Свойства соответствий 1) Рефлексивность 2) Антирефлексивность 3) Симметричность 4) Антисимметричность 5) Транзитивность 1) Не является рефлексивным 2) Не является антирефлексивным 3) Не является симметричным 4) антисимметрично 5) транзитивно 1) рефлексивно 2) антисимметрично 3) транзитивно

Отношения эквивалентности (рефлексивное, симметричное, транзитивное) Отношение подобия на множестве Отношение равномощности множеств треугольников Отношения порядка (антисимметричное, транзитивное) рефлексивное - нестрогое антирефлексивное - строгое M – упорядоченное множество - полный (линейный) порядок - неполный (частичный) порядок

наибольший элемент максимальный элемент либо они не сравнимы наименьший элемент минимальный элемент либо они не сравнимы верхняя граница для Х sup(X) - супремум - наименьшая верхняя граница нижняя граница для Х inf(X) - инфимум - наибольшая нижняя граница наименьший a, наибольшего нет a b множество нижних граней a = inf([a, b)) множество верхних граней b = sup([a, b)) A F O(0, 0)-наименьший элемент максимальные элементы Наибольшего нет F = sup(CAOB) O B O = inf(CAOB)

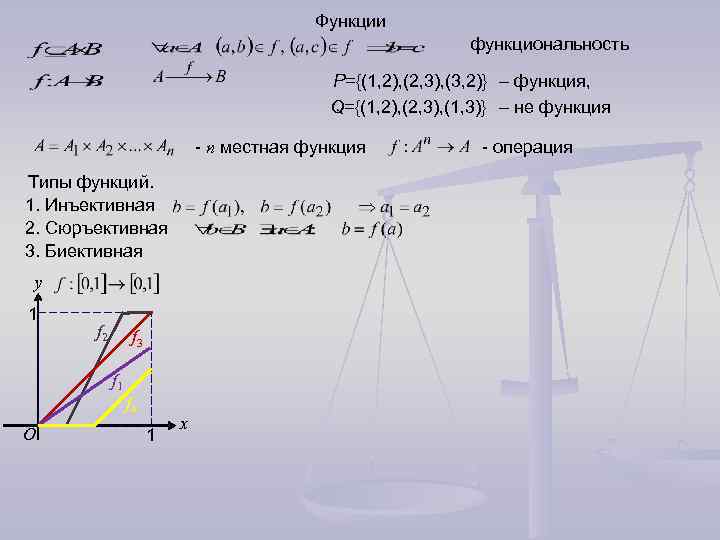
Функции функциональность P={(1, 2), (2, 3), (3, 2)} – функция, Q={(1, 2), (2, 3), (1, 3)} – не функция - n местная функция - операция Типы функций. 1. Инъективная 2. Сюръективная 3. Биективная y 1 f 2 f 3 f 1 f 4 x O 1