Теория катастроф выполнил студент V курса группы КСУ-51

Теория катастроф выполнил студент V курса группы КСУ-51 Ярифа Михаил

Флаги катастроф – наличие нескольких различных (устойчивых) состояний; – существование неустойчивых состояний, из которых система выводится слабыми “толчками"; – возможность быстрого изменения системы при малых изменениях внешних условий; – необратимость системы (невозможность вернуться к прежним условиям); – гистерезис.

I универсальный закон: в окрестности некритической точки приращение функции почти пропорционально приращению аргумента. II универсальный закон: в окрестности максимума (минимума) приращение типичной функции почти пропорционально квадрату приращения аргумента.

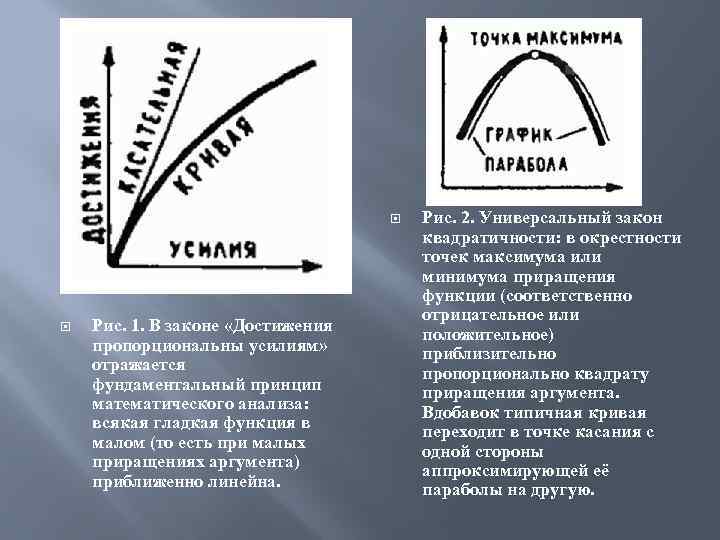Рис. 1. В законе «Достижения пропорциональны усилиям» отражается фундаментальный принцип математического анализа: всякая гладкая функция в малом (то есть при малых приращениях аргумента) приближенно линейна. Рис. 2. Универсальный закон квадратичности: в окрестности точек максимума или минимума приращения функции (соответственно отрицательное или положительное) приблизительно пропорционально квадрату приращения аргумента. Вдобавок типичная кривая переходит в точке касания с одной стороны аппроксимирующей её параболы на другую.

III универсальный закон: типичная плоская кривая касается прямой не более, чем в двух точках. IV универсальный закон: типичная поверхность не касается никакой прямой более, чем в четырех точках.

Рис. 3. Как спасти хвостовое оперение реактивного самолета от струи раскаленных газов? Небольшое отклонение значения аргумента от оптимального практически не сказывается на значении функции. В частности, малый поворот реактивных двигателей не меняет результирующую силу тяги.

V УНИВЕРСАЛЬНОЕ ПРАВИЛО: ПРИ ПЛАВНОМ ПЕРЕХОДЕ ОТ ОДНОГО ЛОКАЛЬНО-ОПТИМАЛЬНОГО РЕЖИМА К ДРУГОМУ НЕОБХОДИМО ВРЕМЕННОЕ УХУДШЕНИЕ.

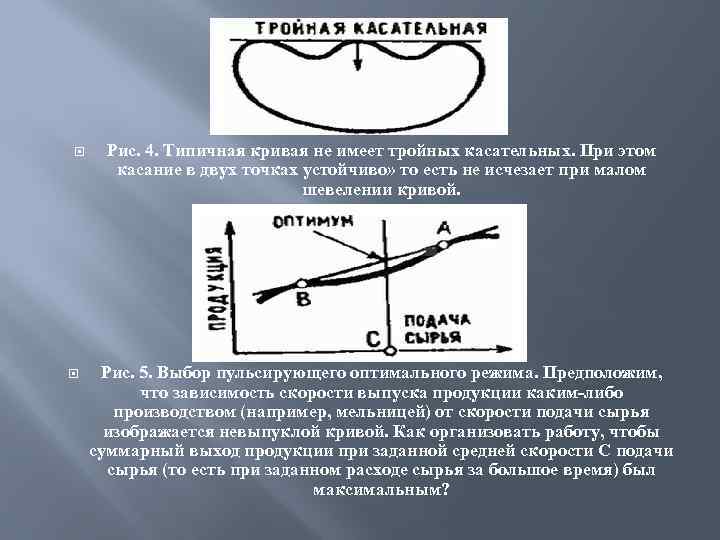Рис. 4. Типичная кривая не имеет тройных касательных. При этом касание в двух точках устойчиво» то есть не исчезает при малом шевелении кривой. Рис. 5. Выбор пульсирующего оптимального режима. Предположим, что зависимость скорости выпуска продукции каким-либо производством (например, мельницей) от скорости подачи сырья изображается невыпуклой кривой. Как организовать работу, чтобы суммарный выход продукции при заданной средней скорости С подачи сырья (то есть при заданном расходе сырья за большое время) был максимальным?

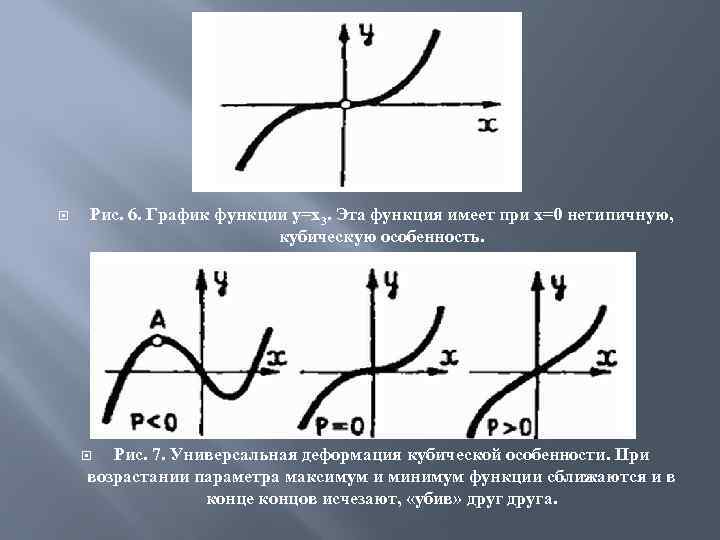Рис. 6. График функции у=х3. Эта функция имеет при х=0 нетипичную, кубическую особенность. Рис. 7. Универсальная деформация кубической особенности. При возрастании параметра максимум и минимум функции сближаются и в конце концов исчезают, «убив» друга.

VI УНИВЕРСАЛЬНОЕ ПРАВИЛО: РАССТОЯНИЕ ОТ ИСЧЕЗАЮЩЕГО ЛОКАЛЬНО-ОПТИМАЛЬНОГО РЕЖИМА ДО ДВИЖУЩЕГОСЯ ЕМУ НАВСТРЕЧУ ЛОКАЛЬНО-МИНИМАЛЬНОГО - ПОРЯДКА КВАДРАТНОГО КОРНЯ ИЗ ОТЛИЧИЯ ПАРАМЕТРА ОТ КАТАСТРОФИЧЕСКОГО ЗНАЧЕНИЯ. ПОЭТОМУ В МОМЕНТ КАТАСТРОФЫ ОБА РЕЖИМА СБЛИЖАЮТСЯ С БЕСКОНЕЧНОЙ СКОРОСТЬЮ. ЭТО, КСТАТИ, ОБЪЯСНЯЕТ, ПОЧЕМУ ТАК ТРУДНО БОРОТЬСЯ С ГРОЗЯЩЕЙ КАТАСТРОФОЙ, КОГДА ЕЁ ПРИЗНАКИ СДЕЛАЛИСЬ УЖЕ ЗАМЕТНЫМИ.

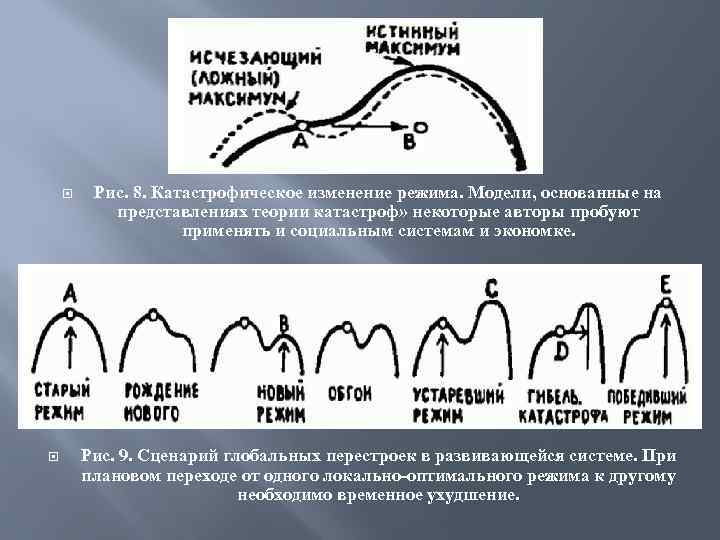Рис. 8. Катастрофическое изменение режима. Модели, основанные на представлениях теории катастроф» некоторые авторы пробуют применять и социальным системам и экономке. Рис. 9. Сценарий глобальных перестроек в развивающейся системе. При плановом переходе от одного локально-оптимального режима к другому необходимо временное ухудшение.

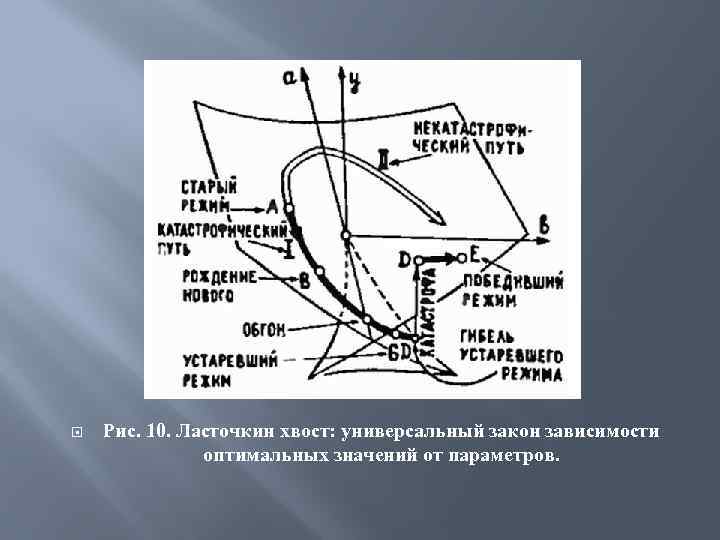Рис. 10. Ласточкин хвост: универсальный закон зависимости оптимальных значений от параметров.

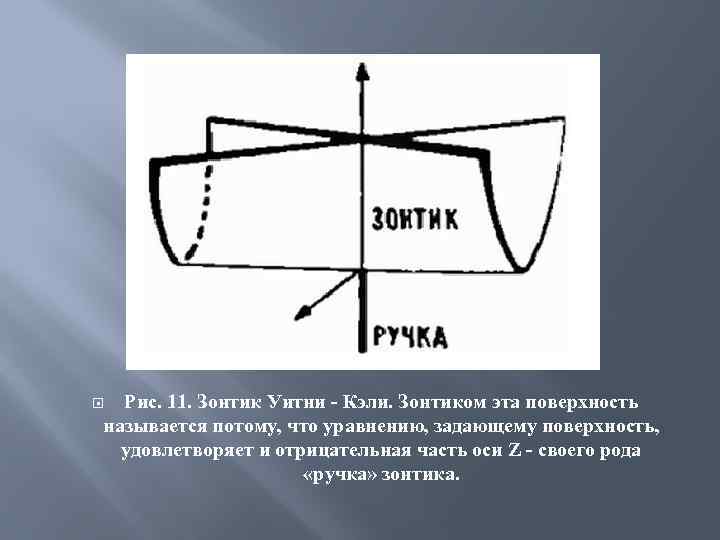Рис. 11. Зонтик Уитни - Кэли. Зонтиком эта поверхность называется потому, что уравнению, задающему поверхность, удовлетворяет и отрицательная часть оси Z - своего рода «ручка» зонтика.

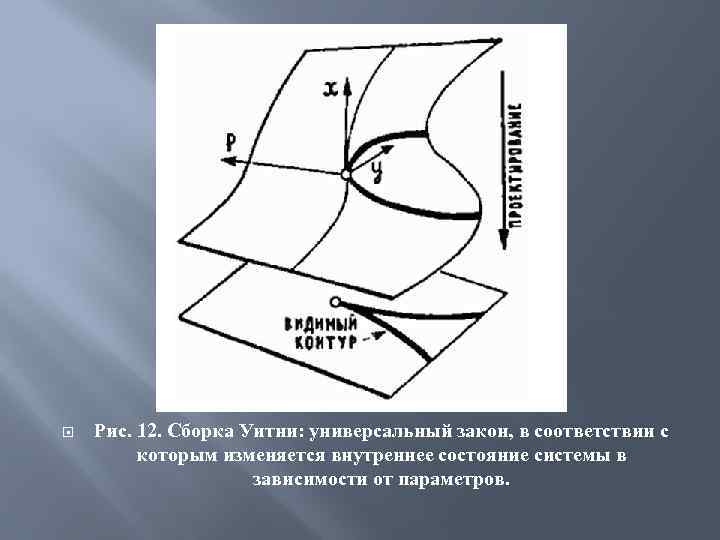Рис. 12. Сборка Уитни: универсальный закон, в соответствии с которым изменяется внутреннее состояние системы в зависимости от параметров.

Рис. 13. Особенность, называемая складкой, возникает, в частности, при проектировании сферы на плоскость в точках экватора.

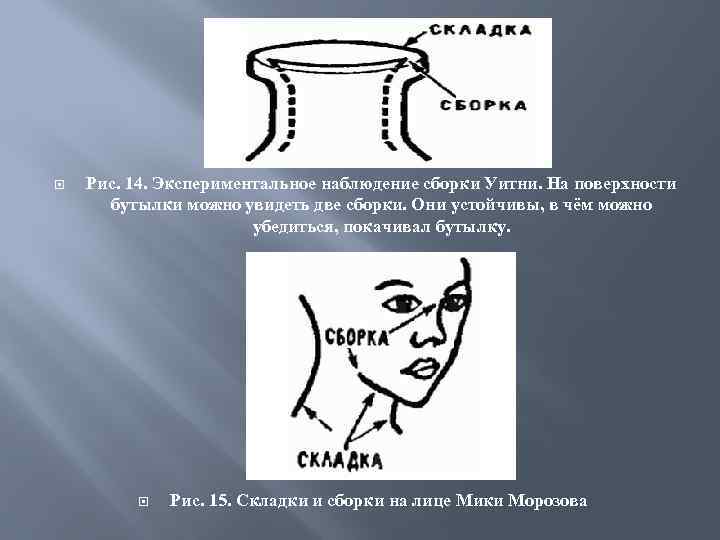Рис. 14. Экспериментальное наблюдение сборки Уитни. На поверхности бутылки можно увидеть две сборки. Они устойчивы, в чём можно убедиться, покачивал бутылку. Рис. 15. Складки и сборки на лице Мики Морозова