Теорія ймовірності та математична статистика Імовірність Неможливі

Теорія ймовірності та математична статистика Імовірність

Неможливі і достовірні події 0 Р(А) 1 ПРАВИЛО СКЛАДАННЯ ЙМОВІРНОСТЕЙ події A 1 ; A 2 ; …… An їх імовірності Р(A 1); Р(A 2) ; … Р(An) Р(A 1 або A 2 …. або An) = =Р(A 1)+Р(A 2)+…+Р(An) =

Повна система подій Р(A 1)+Р(A 2)+…+Р(An) = 1 Повну систему подій утворюють тільки несумісні події. ПОНЯТТЯ УМОВНОЇ ЙМОВІРНОСТІ РВ(А) – імовірність виникнення події А при умові, що подія В сталася.

Правило множення ймовірностей умовних подій P( A і B ) = Р(В) РB(A) = Р(А) РА(В) незалежних подій Р(А і В)==Р(А)Р(В) р(A 1 і A 2 і … і An ) = Р(A 1)Р(A 2)…Р(An) = =

Ймовірність настання щонайменше однієї з незалежних подій р(A 1 або A 2 або … або An ) = Коли ймовірності однакові для всіх подій р(A 1 або A 2 або … або An ) =

Узагальнення правил складення і множення ймовірностей Р(А або В) = Р(А) + Р(В) - Р(А і В). Якщо події А і В несумісні, то Р(А і В)= 0. Якщо події А і В взаємно незалежні, то Р(А і В) = Р(А)Р(В). Оскільки 0 ≤ Р(А і В), то Р(А або В) ≤ Р(А) + Р(В)

Формули комбінаторики • Перестановки Аnm • Розміщення Pm= m! • Сполучення Cnm

Нехай, в урні а білих і b чорних куль; з урни наздогад виймають k куль. Знайти ймовірність того, що серед, них буде l білих, а, значить, k – l чорних (l ≤ а, k- l ≤b).

Формула повної ймовірності Події A 1 ; A 2 ; …… An Їх імовірності Р(A 1); Р(A 2) ; … Р(An) Імовірності виходу К РА 1(К) ; РА 2(К) ; … ; РАn(К) для будь-якого можливого результату K цієї операції ймовірність її настання буде

Формула Байєса Нехай події А 1, А 2, . , Аn являють собою повну систему подій. Якщо тоді К означає довільний результат цієї операції, то ймовірність того, що цей довільний результат стався внаслідок q-ї операції, (1≤q≤n)

Формула Бернуллі Уточнення формули Байєса для багаторазових випробувань

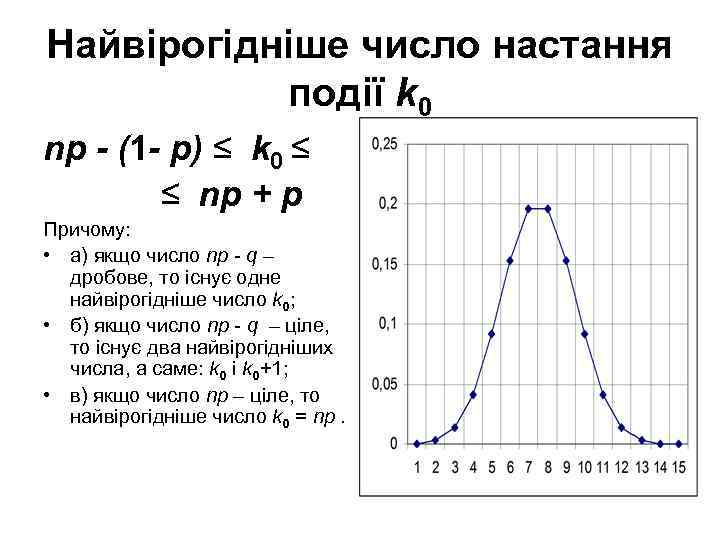Найвірогідніше число настання події k 0 np - (1 - p) ≤ k 0 ≤ ≤ np + p Причому: • а) якщо число np - q – дробове, то існує одне найвірогідніше число k 0; • б) якщо число np - q – ціле, то існує два найвірогідніших числа, а саме: k 0 і k 0+1; • в) якщо число np – ціле, то найвірогідніше число k 0 = np.

Теорема Бернуллі. Перша форма закону великих чисел + εn - εn nр

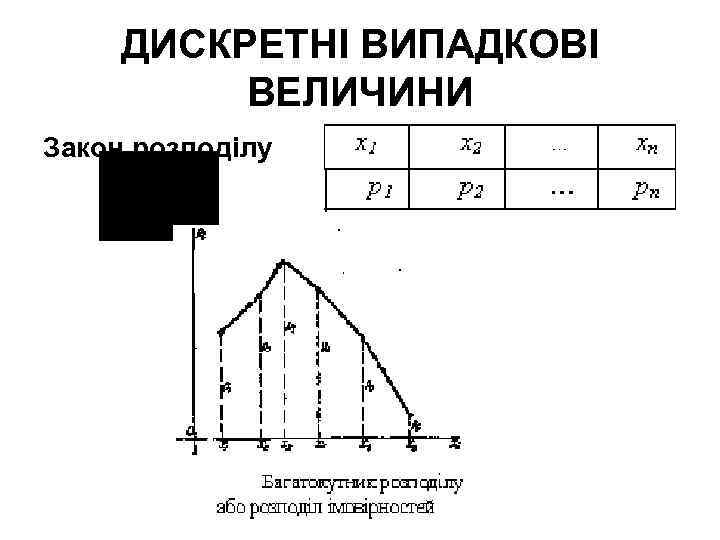ДИСКРЕТНІ ВИПАДКОВІ ВЕЛИЧИНИ Закон розподілу

Числові характеристики дискретної випадкової величини μ 1= 0; μ 2= α 2 - α 12; μ 3= α 3 - 3α 1α 2+2α 13; μ 4= α 4 - 4α 12α 3+3α 2α 3 -4α 14. α 1 = mx, M[X] , μ 2 = Dx, D[X], Qx 2, q 2, σx 2

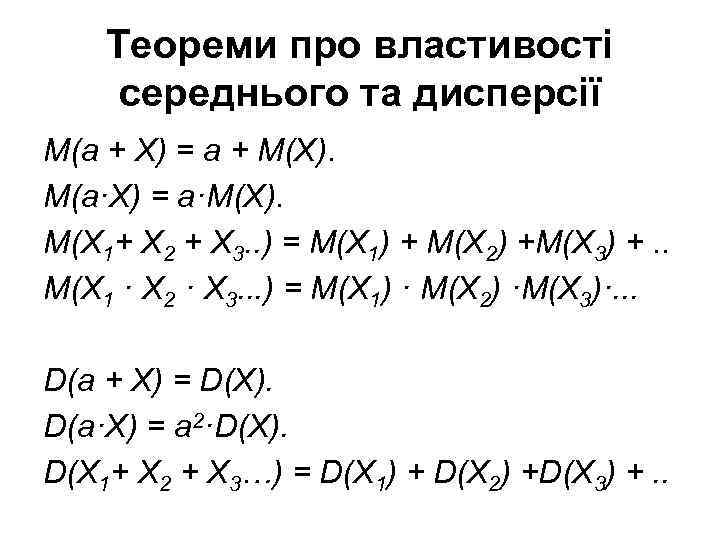Теореми про властивості середнього та дисперсії М(а + Х) = а + М(Х). М(а·Х) = а·М(Х). М(Х 1+ Х 2 + Х 3. . ) = М(Х 1) + М(Х 2) +М(Х 3) +. . М(Х 1 · Х 2 · Х 3. . . ) = М(Х 1) · М(Х 2) ·М(Х 3)·. . . D(а + Х) = D(Х). D(а·Х) = а 2·D(Х). D(Х 1+ Х 2 + Х 3…) = D(Х 1) + D(Х 2) +D(Х 3) +. .

Теореми про середнє квадратичне відхилення Маємо випадкові величини х1, х2, …, хn зі стандартами q 1, q 2, …, qn середнє арифметичне =(х1+х2+…+хn)/n результатів n вимірювань. Тоді стандарт цього середнього, при умові що всі стандарти однакові

Нерівність Чєбишева -ε +ε М[X]

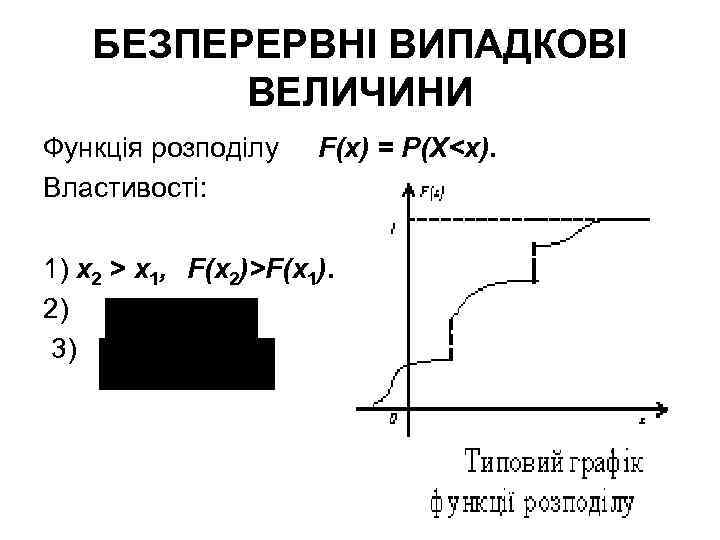БЕЗПЕРЕРВНІ ВИПАДКОВІ ВЕЛИЧИНИ Функція розподілу Властивості: F(х) = Р(X<х). 1) х2 > х1, F(х2)>F(х1). 2) 3)

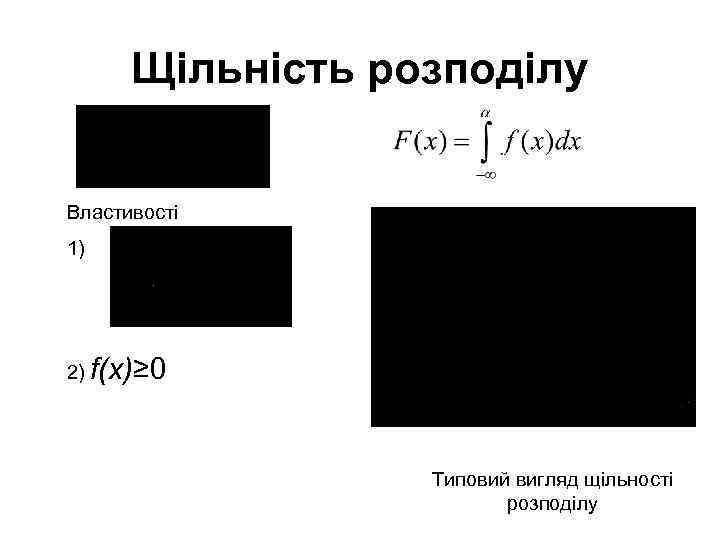Щільність розподілу Властивості 1) 2) f(x)≥ 0 Типовий вигляд щільності розподілу

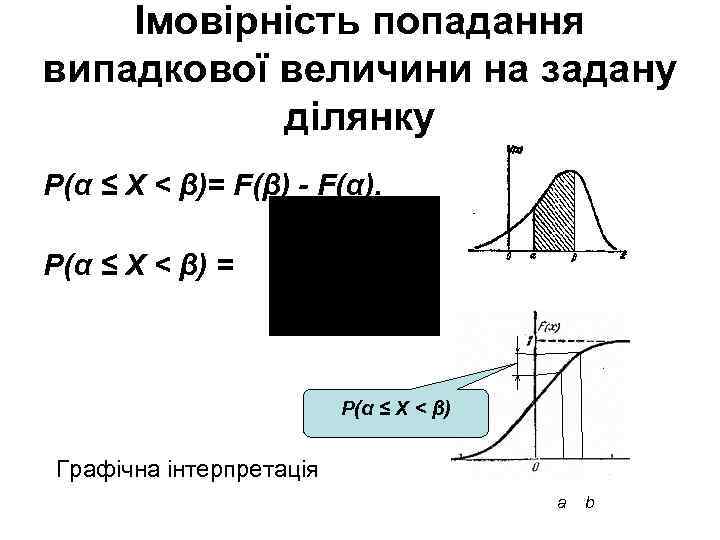Імовірність попадання випадкової величини на задану ділянку P(α ≤ Х < β)= F(β) - F(α). P(α ≤ Х < β) = P(α ≤ Х < β) Графічна інтерпретація a b

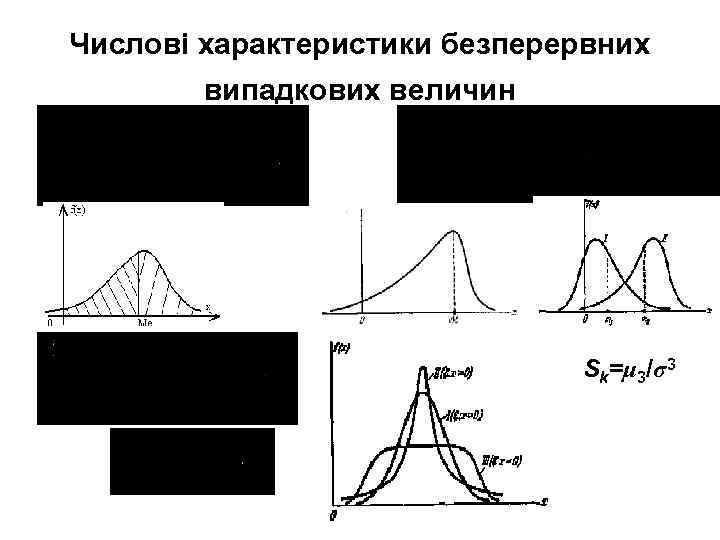Числові характеристики безперервних випадкових величин Sk=μ 3/σ3

Закон рівномірної щільності f(х)=1/(β-α), при f(х)=0 при х < α або х > β F(х) = 0, при х < α; F(х) = (х-α)/(β-α), при F(х) = 1 при х > β

Експоненціальний закон розподілу P(a

Закон Пуассона R 1 = 1 - Рm = 1 - ℮-а

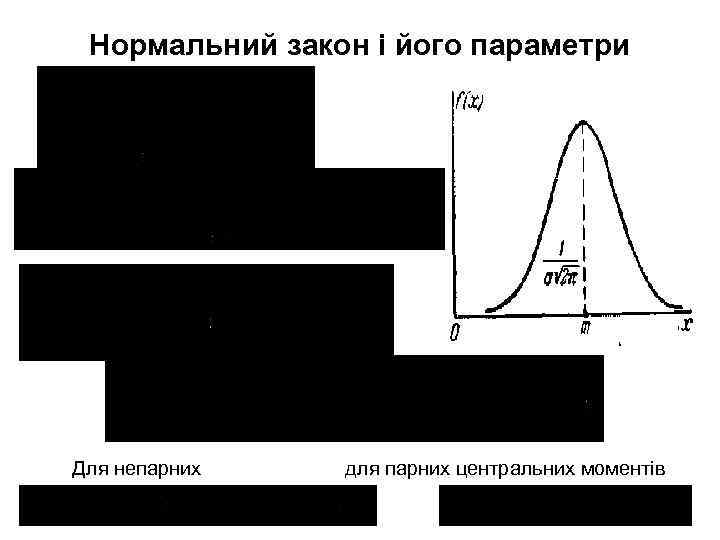Нормальний закон і його параметри Для непарних для парних центральних моментів

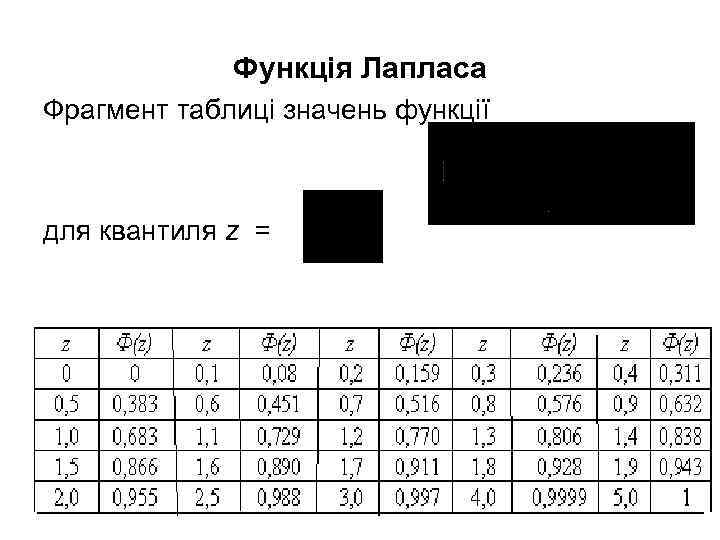Функція Лапласа Фрагмент таблиці значень функції для квантиля z =

Теореми Лапласа Локальна Інтегральна Відхилення відносної частоти від постійної імовірності в незалежних дослідженнях

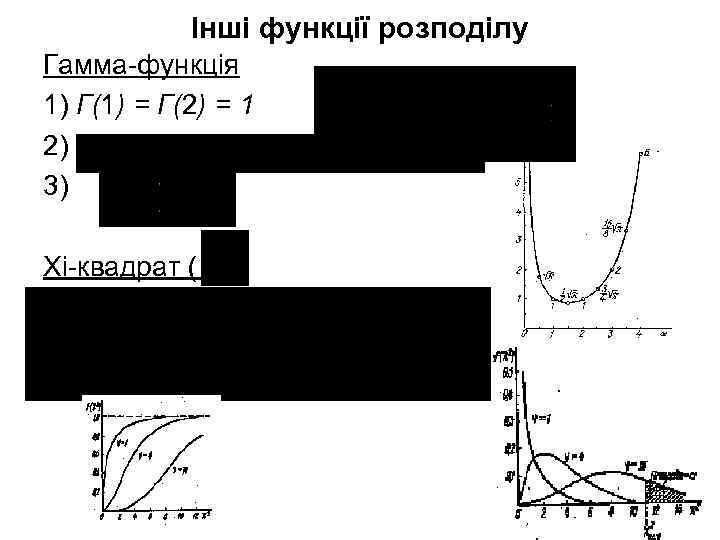Інші функції розподілу Гамма-функція 1) Г(1) = Г(2) = 1 2) 3) Хі-квадрат ( )

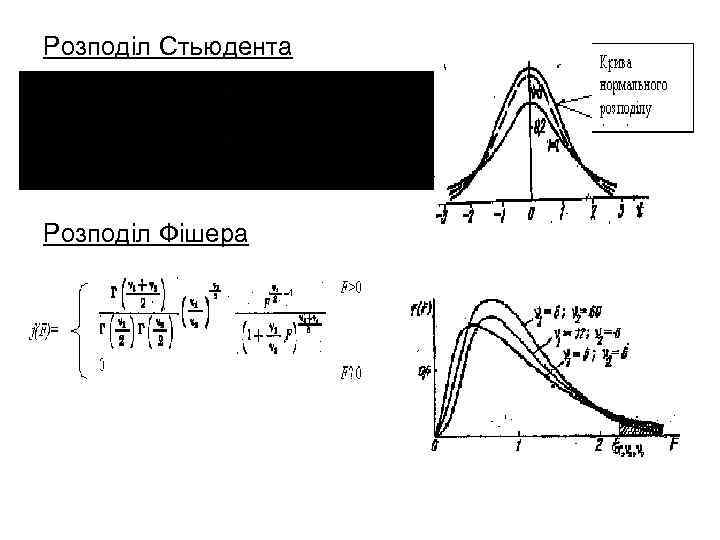Розподіл Стьюдента Розподіл Фішера

Поняття про теорію масового обслуговування ρ0=0

Поняття про теорію надійності Імовірність безвідмовної роботи в інтервалі t 0 - t Імовірність безвідмовної роботи в інтервалі t 0 – t, якщо він вже працював безвідмовно у попередньому інтервалі 0 - t 0 Імовірність безвідмовної роботи з резервом

Центральна гранична теорема Теорема Ляпунова Теорема Муавра-Лапласа

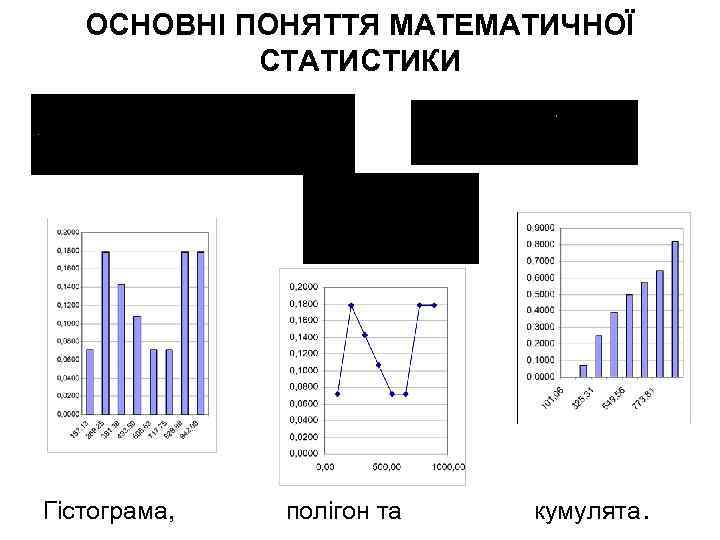ОСНОВНІ ПОНЯТТЯ МАТЕМАТИЧНОЇ СТАТИСТИКИ Гістограма, полігон та кумулята.

Оцінки числових характеристик випадкової величини

Закон великих чисел. Теорема Чєбишева

Довірчий інтервал P(| - |<ε)= β Де Л(β)– зворотне значення функції Лапласа для квантиля таблиці z=

Віднесення випадкової величини до певного закону розподілу Р(хі