Теория изгиба пластин.pptx
- Количество слайдов: 43

Теория изгиба пластин 1 Общие положения. Гипотезы Кирхгофа

Пластиной называют плоское тело, ограниченное двумя плоскостями, расстояние между которыми мало по сравнению с размерами самих поверхностей. Плоскость, равноудаленная от оснований пластинки (делящая размер h пополам), называется срединной плоскостью. Координатная плоскость x. Oy предполагается всегда совпадающей со срединной плоскостью. Под действием поперечной (перпендикулярной срединной плоскости) нагрузки пластинка изгибается и срединная плоскость искривляется, превращаясь в срединную поверхность пластинки (упругую поверхность). Вертикальные перемещения точек срединной поверхности обозначаются и называются прогибами пластинки. В зависимости от формы контура пластины могут быть круглые, прямоугольные, эллиптические и т. д.
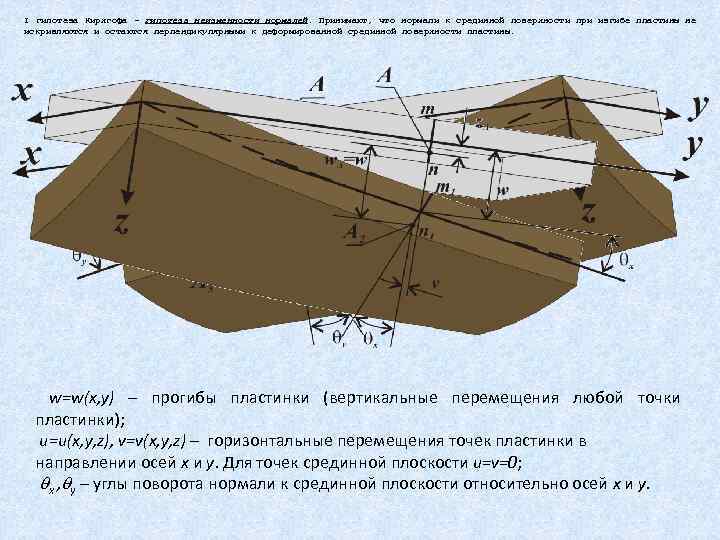
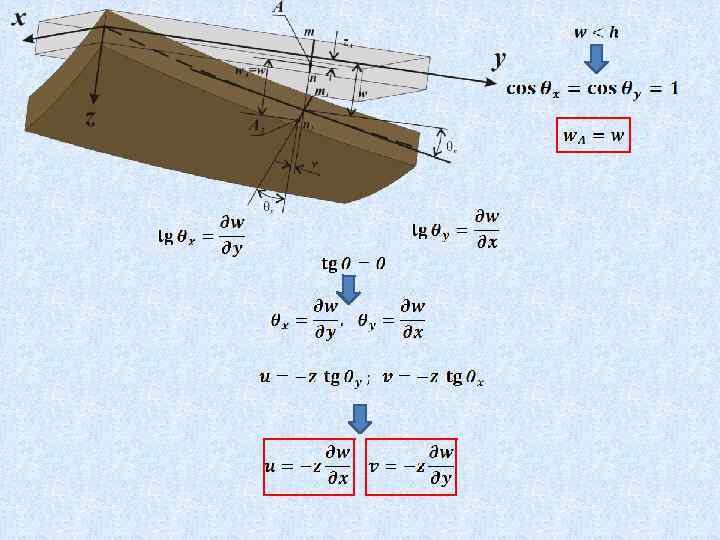
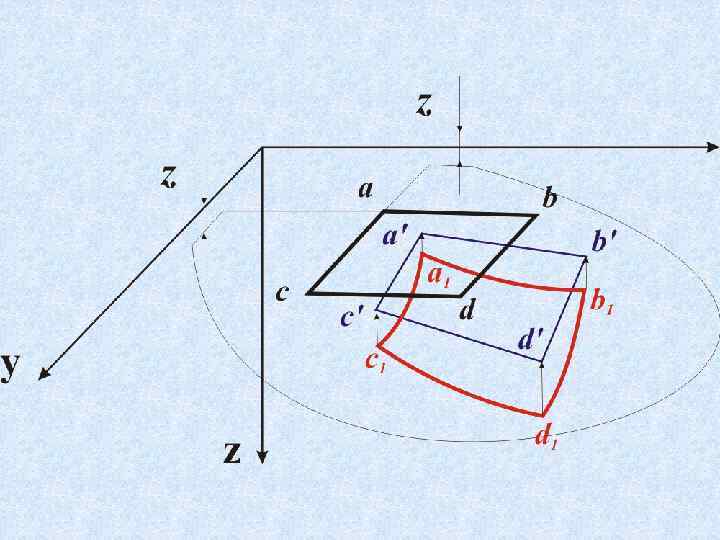
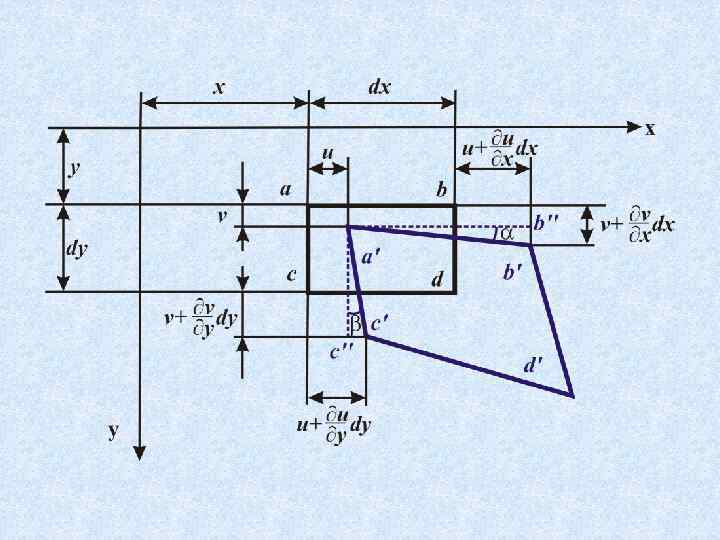
I гипотеза Кирхгофа – гипотеза неизменности нормалей. Принимают, что нормали к срединной поверхности при изгибе пластины не искривляются и остаются перпендикулярными к деформированной срединной поверхности пластины. w=w(x, y) – прогибы пластинки (вертикальные перемещения любой точки пластинки); u=u(x, y, z), v=v(x, y, z) – горизонтальные перемещения точек пластинки в направлении осей x и y. Для точек срединной плоскости u=v=0; x , y – углы поворота нормали к срединной плоскости относительно осей x и y.
II гипотеза Кирхгофа – гипотеза о ненадавливании одного слоя пластины на другой. Согласно этой гипотезе все компоненты напряжений в площадках, перпендикулярные срединной плоскости, считаются пренебрежимо малыми, т. е. напряженное состояние принимается за плоское вместо трехосного. ― толщина пластины мала по сравнению с размерами пластины в плане ― прогиб мал по сравнению с толщиной ― материал пластины – однородный, изотропный и подчиняющийся закону Гука

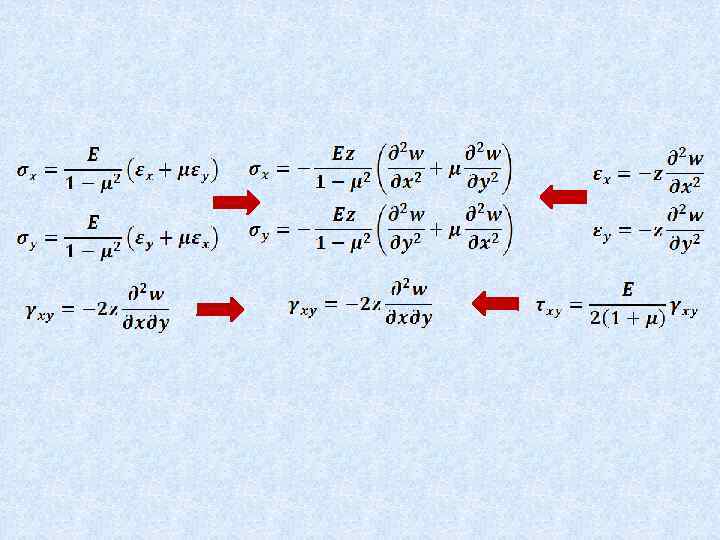
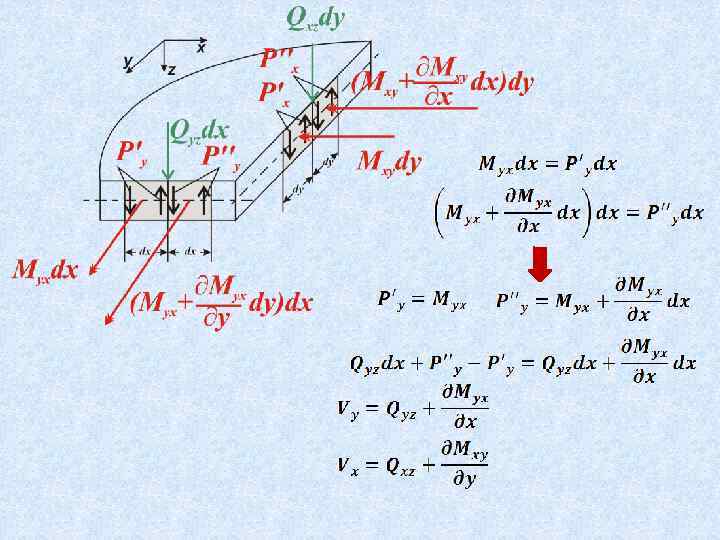
Теория изгиба пластин 2 Напряжения, усилия и моменты в сечениях пластинки
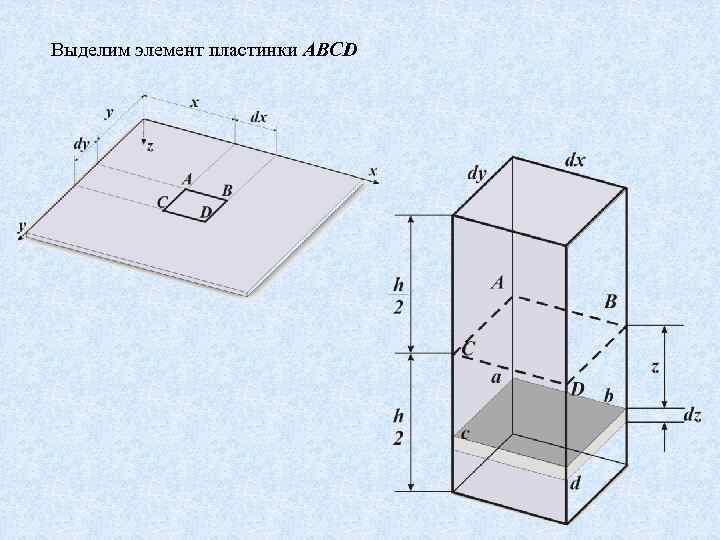
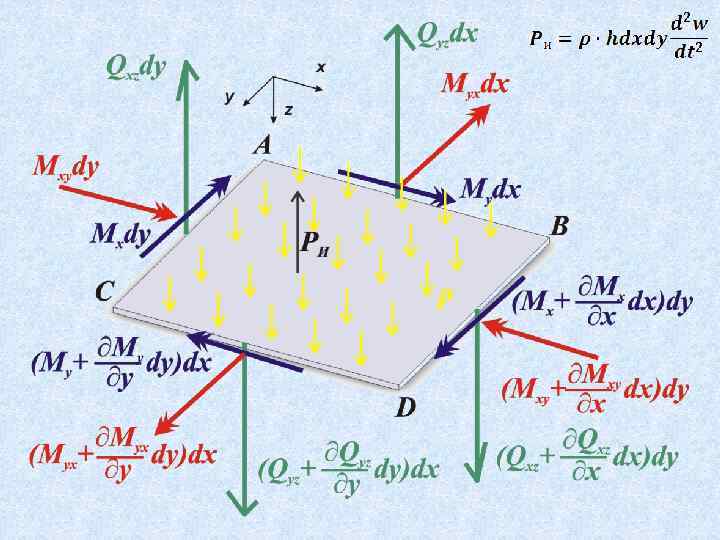
Выделим элемент пластинки ABCD
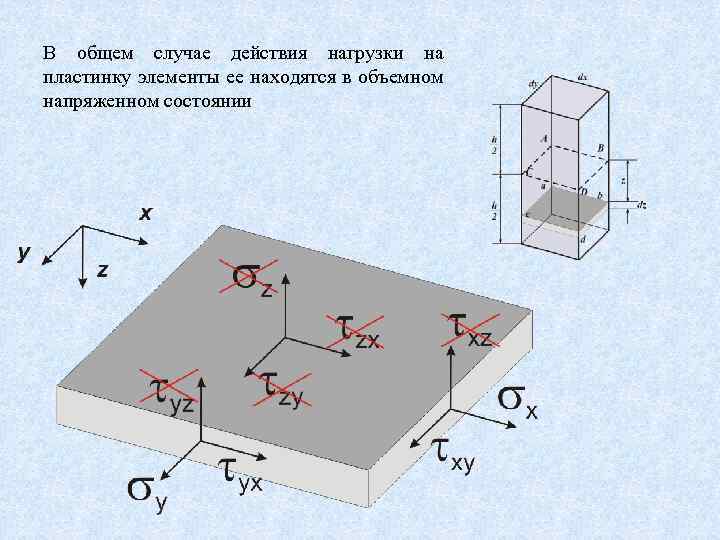
В общем случае действия нагрузки на пластинку элементы ее находятся в объемном напряженном состоянии
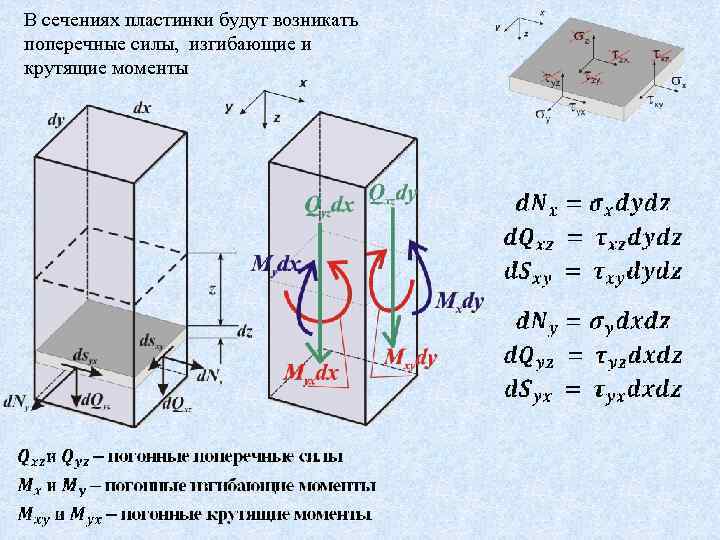
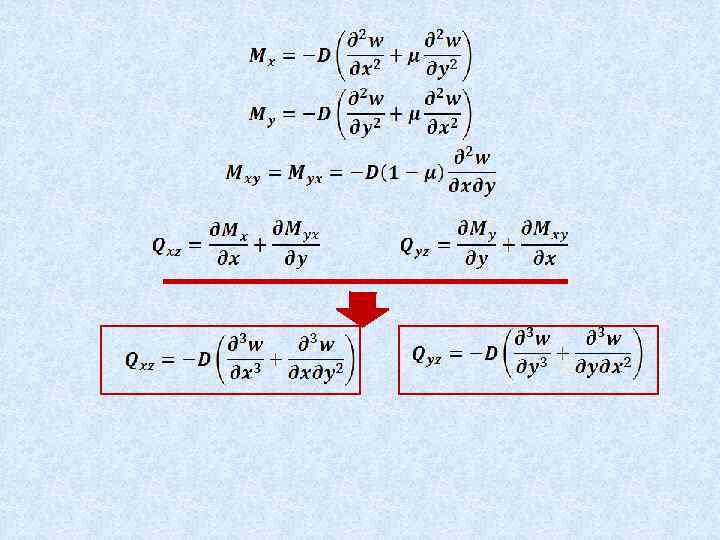
В сечениях пластинки будут возникать поперечные силы, изгибающие и крутящие моменты
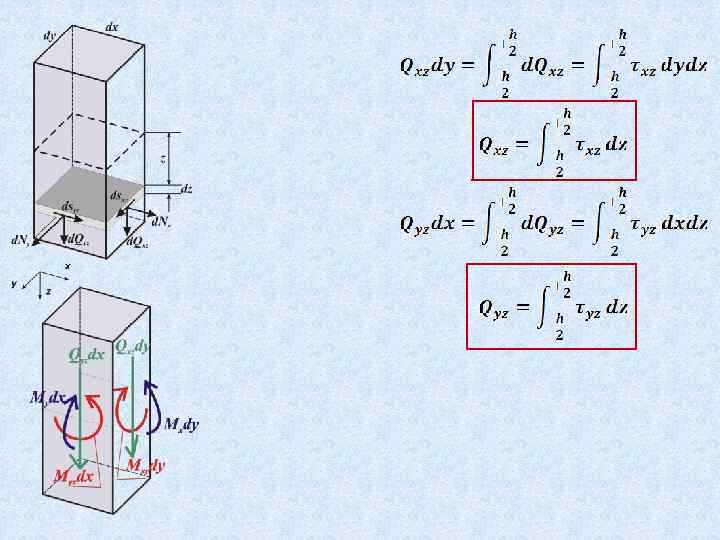
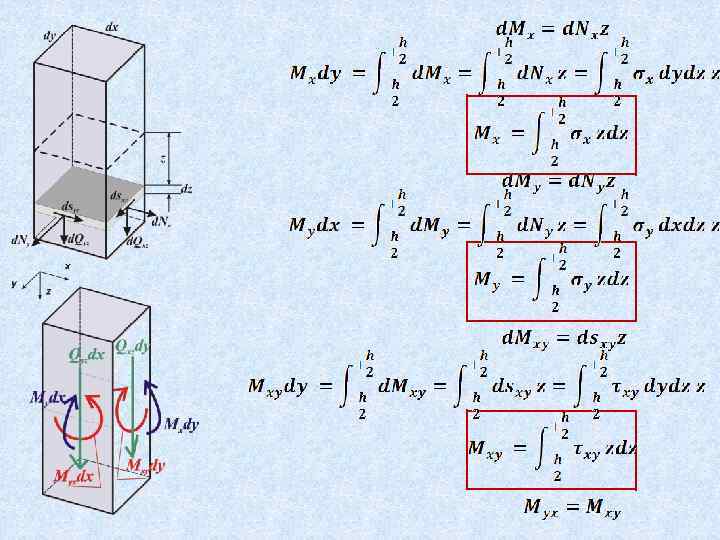
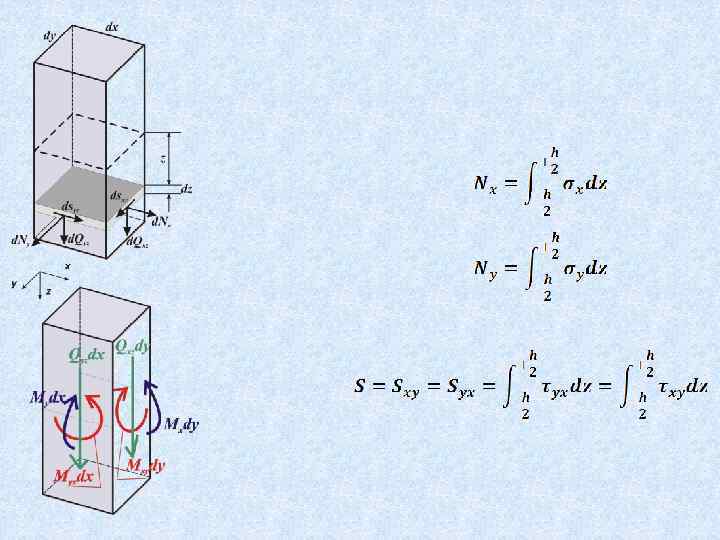
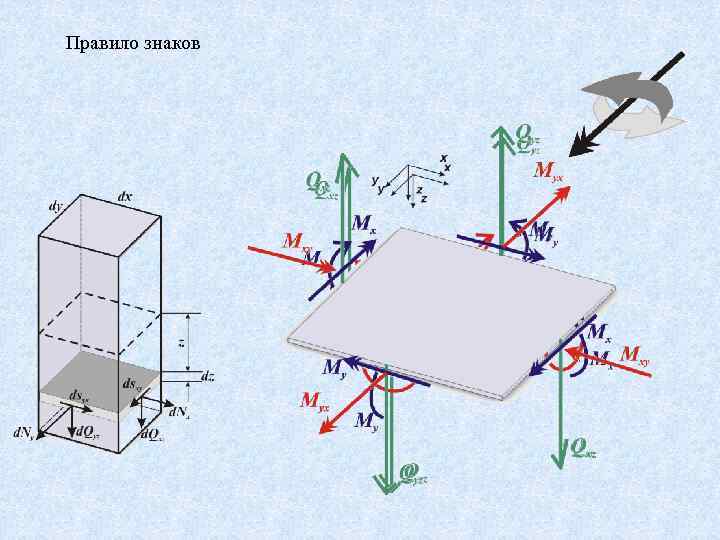
Правило знаков
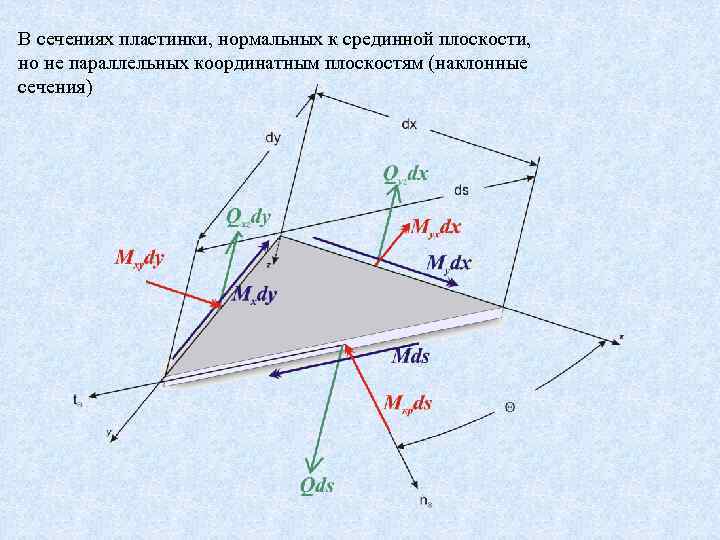
В сечениях пластинки, нормальных к срединной плоскости, но не параллельных координатным плоскостям (наклонные сечения)
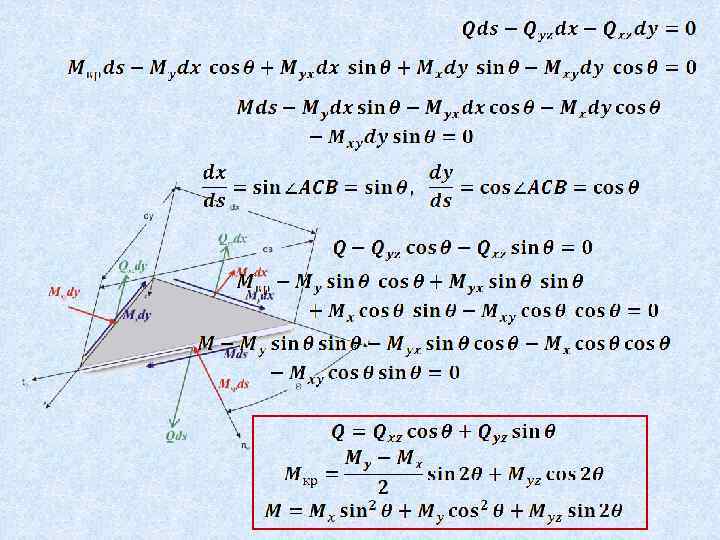

Теория изгиба пластин 3 Вывод основного уравнения изгиба пластин


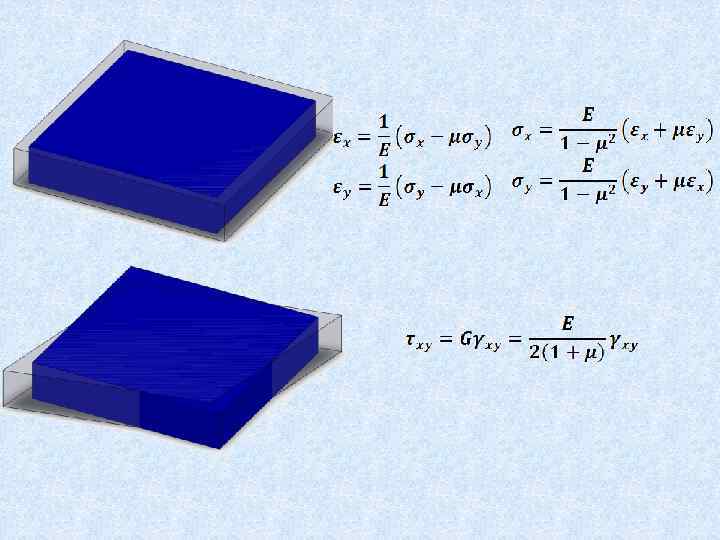

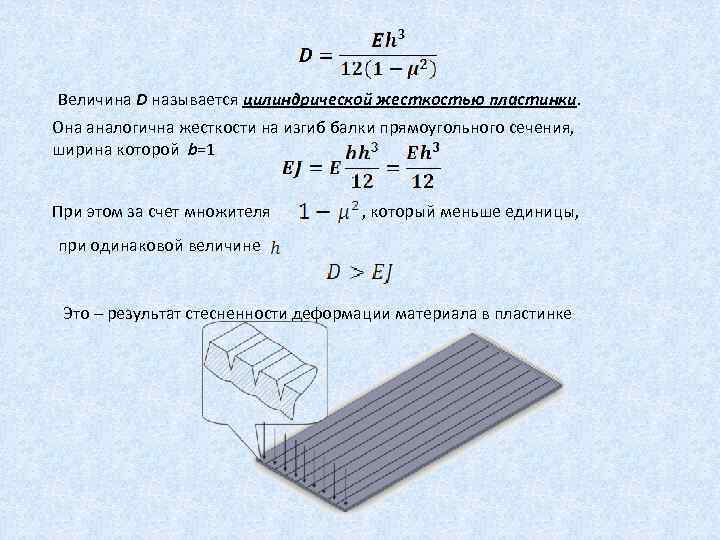
Величина D называется цилиндрической жесткостью пластинки. Она аналогична жесткости на изгиб балки прямоугольного сечения, ширина которой b=1 При этом за счет множителя , который меньше единицы, при одинаковой величине Это – результат стесненности деформации материала в пластинке

Основное уравнение изгиба пластин (Софи Жермен)

Частные случаи уравнения уравнение описывает вынужденные поперечные колебания пластинки, вызванные переменной во времени распределенной нагрузкой уравнение описывает свободные (собственные) поперечные колебания загруженной постоянной нагрузкой пластинки уравнение описывает свободные (собственные) поперечные колебания незагруженной пластинки уравнение поперечного изгиба пластинки

Теория изгиба пластин 4 Закрепления пластинок. Граничные условия
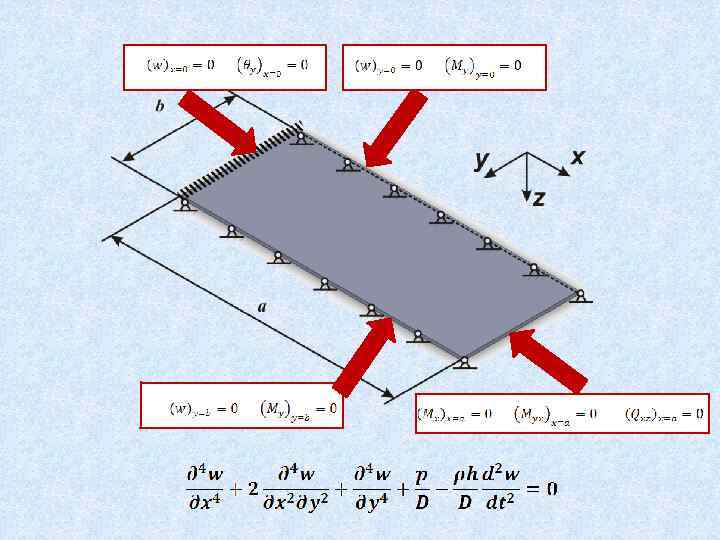
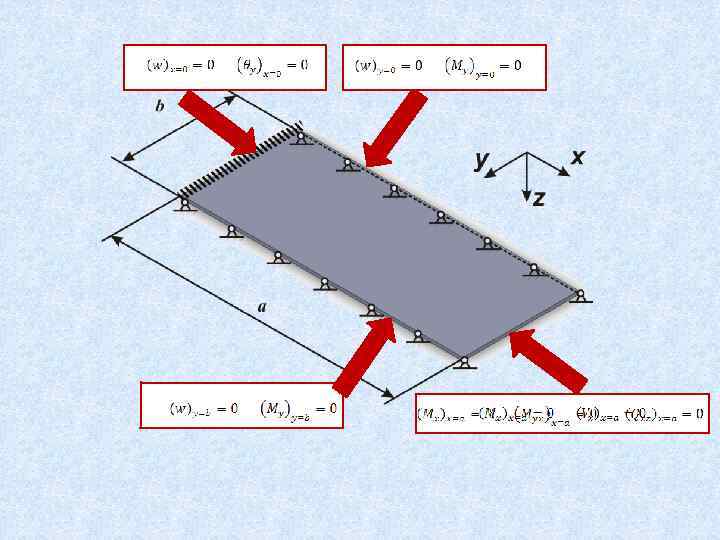

Край свободно оперт Край жестко заделан Край свободен

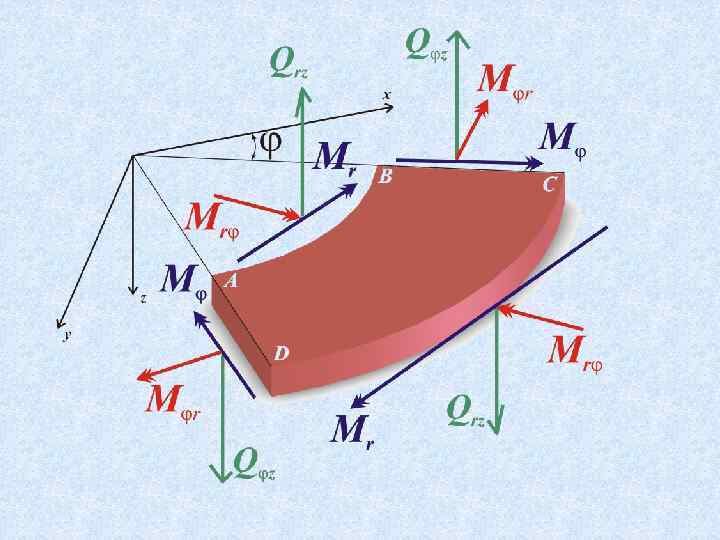
Теория изгиба пластин 5 Основные уравнения поперечного изгиба пластинки в полярных координатах



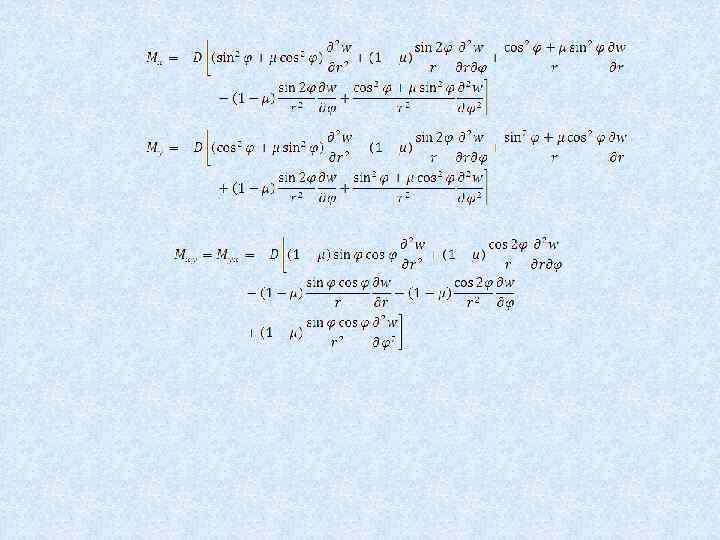
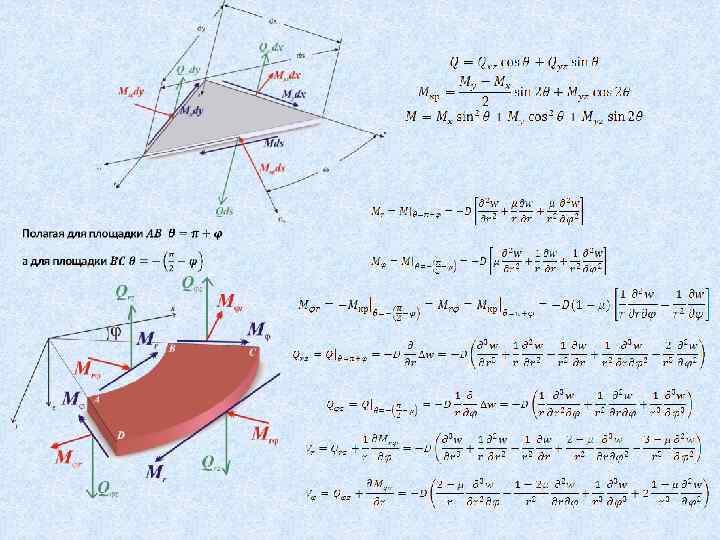


Теория изгиба пластин 6 Приближенные методы решения основного дифференциального уравнения изгиба пластин
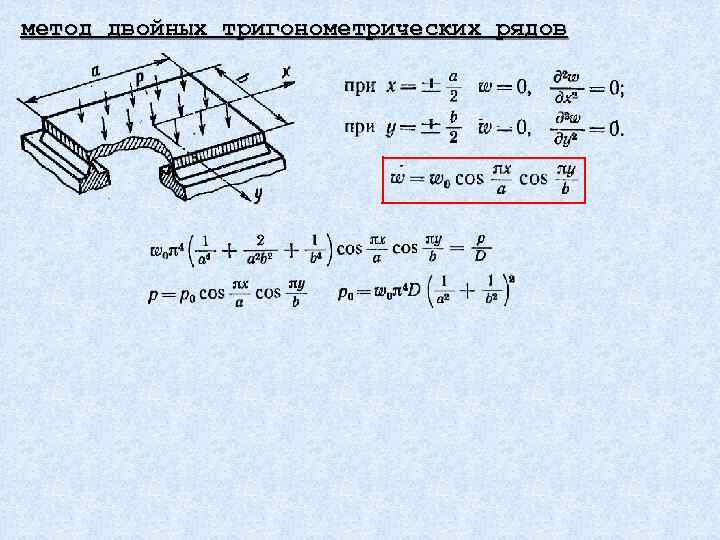
метод двойных тригонометрических рядов
Теория изгиба пластин.pptx