Теория Информационных Процессов Тема 2 Модуляция сигналов

Теория Информационных Процессов Тема № 2: Модуляция сигналов

План l l l l l Общий принцип модуляции Непрерывная модуляция Импульсная модуляция Дискретная модуляция Амплитудная модуляция Частотная модуляция Фазовая модуляция Угловая модуляция Амплитудно-импульсная модуляция

Модуляция Исследование различных видов модуляции необходимо для: • • Определения предельных свойств каналов Сокращения избыточности сигналов Улучшения использования мощных передающих устройств Определение потенциальной помехоустойчивости к помехам соседним каналам, решения проблем электромагнитной совместимости различных систем передачи информации

Общий принцип модуляции Изменение параметров носителя информации S(t, a, b , c, …) в соответствии с передаваемым сообщением (a, b, c, … информационные параметры) S(t) – сигнал (определение см в теме 1)

Непрерывная модуляция Если в качестве физического процесса (носителя информации) выбрано гармоническое колебание с частотой , то В соответствии с (1) может быть три вида модуляции: Амплитудная (АМ) • Частотная (ЧМ) • Фазовая (ФМ) •

Импульсная модуляция Если в качестве носителя информации выбрана последовательность импульсов, то можно различить четыре вида импульсной модуляции (при заданной форме импульса): • • Амплитудно-импульсная (АИМ) Широтно-импульсная (ШИМ) Время-импульсная (ВИМ, ФИМ) Частотно импульсная (ЧИМ)

Дискретная (цифровая) модуляция Закодированное сообщение последовательность кодовых символов. Модуляция – один из параметров «переносчика» меняется по закону, определяемому кодом. При непосредственной передаче «переносчиком» может быть постоянный ток (изменяется величина и направление тока) В качестве «переносчика» как при непрерывной модуляции, может использоваться переменный ток (гармоническое колебание)

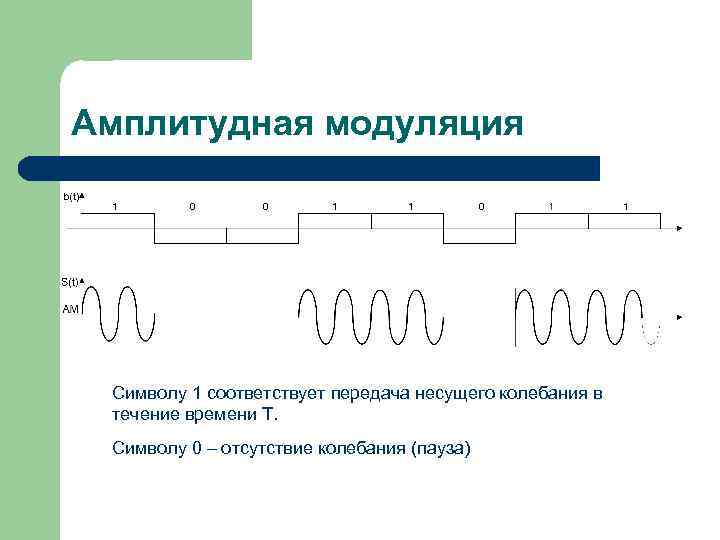Амплитудная модуляция Символу 1 соответствует передача несущего колебания в течение времени Т. Символу 0 – отсутствие колебания (пауза)

Частотная модуляция Символу 1 соответствует передача несущего колебания с частотой 1 Символу 0 – с частотой 2

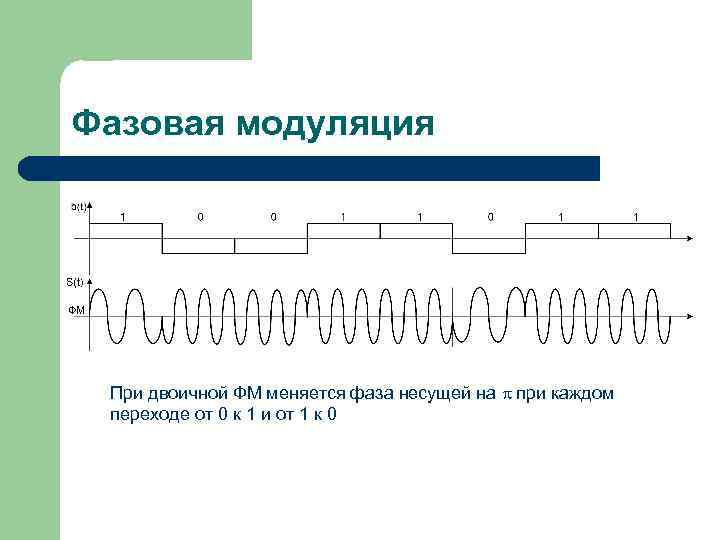Фазовая модуляция При двоичной ФМ меняется фаза несущей на при каждом переходе от 0 к 1 и от 1 к 0

ОФМ В отличие от ФМ фазу сигнала отсчитывают не от некоторого эталона, а от фазы предыдущего элемента сигнала

Виды модуляции

Признаки классификации Для классификации видов модуляции удобно использовать следующие признаки: • • Характер полезного сигнала и переносчика (детерминированный процесс, случайный стационарный процесс, случайный нестационарный процесс) Вид сигналов (аналоговые, дискретные) Вид информационного параметра (амплитуда, частота, форма, длительность, период) И др

Амплитудная модуляция При АМ огибающая амплитуды гармонического колебания (переносчика) изменяется по закону, совпадающему с законом изменения передаваемого сообщения: 0 – частота переносчика

Амплитудная модуляция Основной параметр АМ-колебания – коэффициент модуляции (М) М определяется для случая, когда модулирующая функция (сообщение) является гармоническим колебанием - частота модуляции

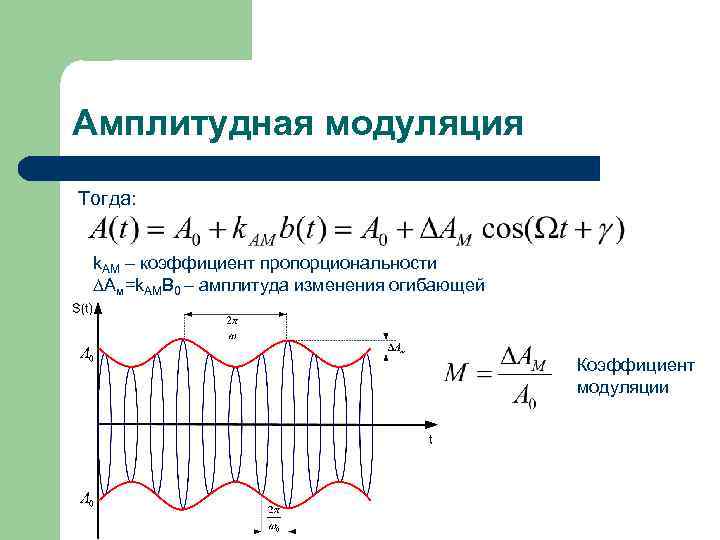Амплитудная модуляция Тогда: k. АМ – коэффициент пропорциональности Ам=k. AMB 0 – амплитуда изменения огибающей Коэффициент модуляции

Амплитудная модуляция Тогда: Для определения технических характеристик канала связи необходимо знать спектр модулированного колебания (передаваемого сигнала)

Амплитудная модуляция Найдем спектр для гармонической (тональной) модуляции (2) После преобразования (3): 1 -е слагаемое – исходное немодулированное колебание с частотой 0 2 -е и 3 -е слагаемые – новые колебания, появившиеся в спектре S(t) в результате модуляции

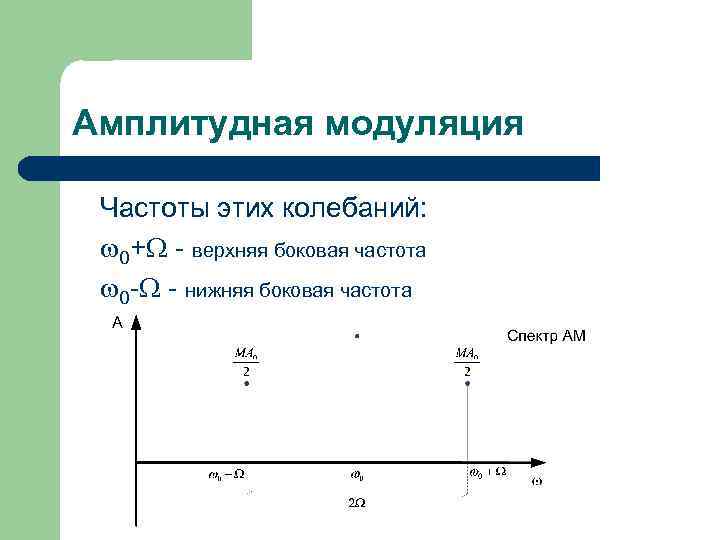Амплитудная модуляция Частоты этих колебаний: 0+ - верхняя боковая частота 0 - - нижняя боковая частота

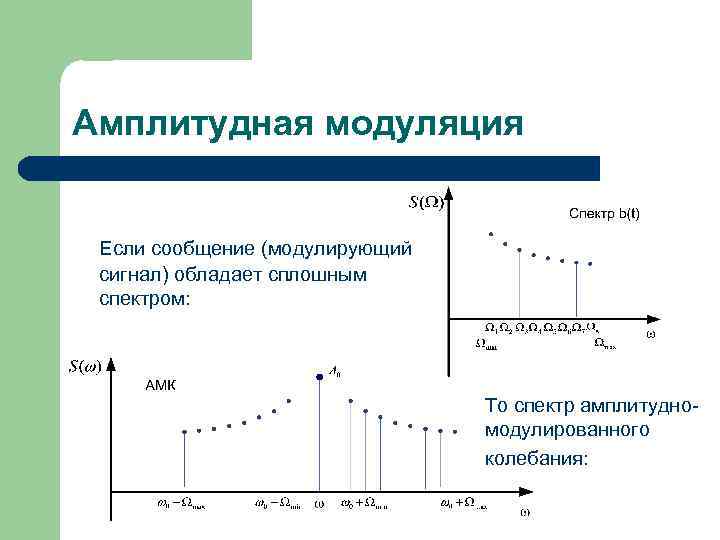Амплитудная модуляция Если сообщение (модулирующий сигнал) обладает сплошным спектром: То спектр амплитудномодулированного колебания:

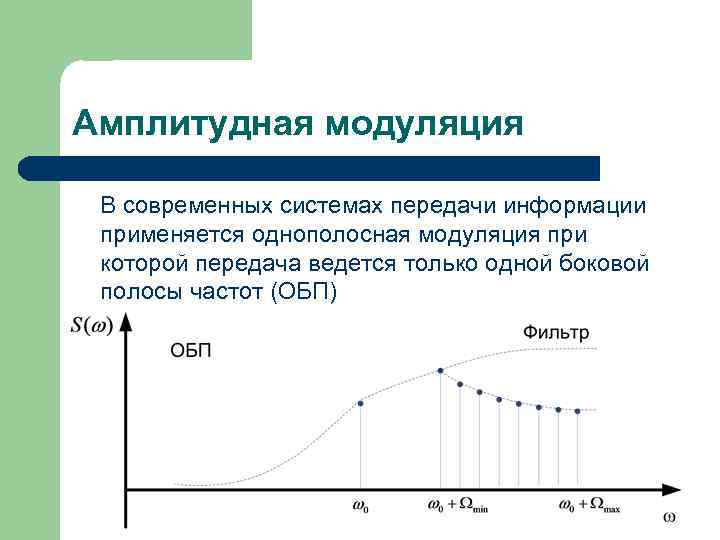Амплитудная модуляция В современных системах передачи информации применяется однополосная модуляция при которой передача ведется только одной боковой полосы частот (ОБП)

Угловая модуляция ЧМ и ФМ часто объединяют под общим названием угловой модуляции Для простого гармонического колебания Набег фаз за промежутки времени от t 1 до t 2 Итак: при постоянной угловой частоте набег фазы за какой-то промежуток времени пропорциональна этому промежутку

Угловая модуляция С другой стороны, если известен пробег фазы за t 2 -t 1, то угловую частоту можно определить как отношение: Отсюда: Угловая частота есть не что иное как скорость изменения фазы колебания В случае сплошного колебания, частота которого меняется во времени: (t) – мгновенная частота колебания (угловая )

Угловая модуляция При этом фаза колебания в момент t Эти соотношения устанавливают связь между изменением частоты и фазы, указывают на общность двух разновидностей угловой модуляции – ЧМ и ФМ Рассмотрим простейшую гармоническую ЧМ g – амплитуда частотного отклонения – девиация частоты 0 – несущая частота - модулирующая частота

Угловая модуляция амплитуда колебания постоянна: Тогда Позволяет трактовать это колебание как модулированное по фазе Модуляция частоты по закону фазы по закону приводит к модуляции

Угловая модуляция Амплитуда уменьшения фазы m – индекс угловой модуляции (m не зависит от 0) Противоположный случай: простейшее гармоническое ФМ колебание Тогда: Используя (5): Учитывая предыдущие формулы: Итак, гармоническая модуляция фазы с индексом max эквивалентна частотной модуляции с девиацией

Угловая модуляция Таким образом, при гармонической угловой модуляции по характеру колебания нельзя заключить с какой модуляцией мы имеем дело – ЧМ или ФМ Иное положение при негармоническом модулирующем колебании. В этом случае вид модуляции можно установить по характеру изменения частоты и фазы во времени!

Угловая модуляция При гармоническом модулирующем сигнале различие между ЧМ и ФМ можно выявить только изменяя частоту модуляции При ЧМ (7) -> g – пропорционально амплитуде модулирующего параметра и не зависит от При ФМ (9) -> max – пропорционально амплитуде и не зависит от (10) -> девиация частоты пропорционально m и частоте

Спектр колебания при гармонической угловой модуляции Начальные фазы 0 и опущены В теории функций Бесселя доказываются следующие отношения:

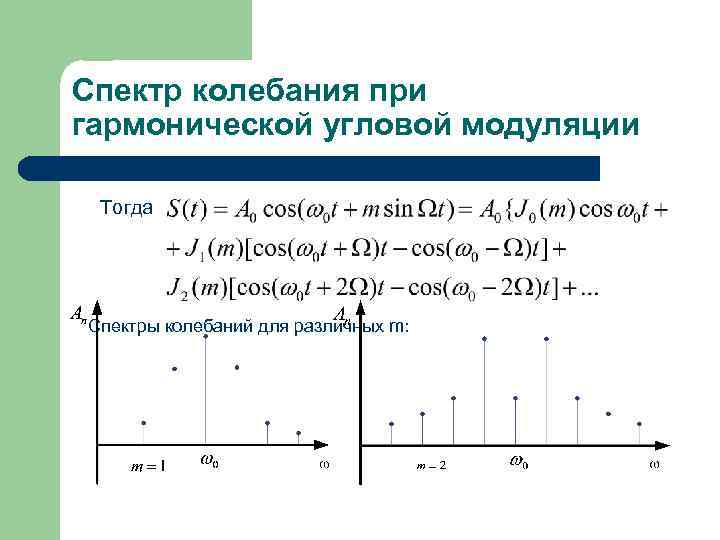Спектр колебания при гармонической угловой модуляции Тогда Спектры колебаний для различных m:

Спектр колебания при гармонической угловой модуляции При больших m (m>>1) Jn(m) быстро убывает до 0 Это дает возможность определить ширину спектра колебаний с угловой модуляцией: max – максимальное число спектральных составляющих но При больших индексах модуляции ширина спектра модулированных ФМ и ЧМ колебаний близка к удвоенной девиации частоты

Особенности спектра ЧМ – колебания: При увеличении m – уменьшается ~ Спектральные составляющие раздвигаются, а учитывая из количество уменьшается Ширина спектра практически не зависит от ФМ – колебания: При увеличении m – не меняется Амплитуды спектральных составляющих при m=const не меняются Составляющие спектра - раздвигаются Спектр расширяется с ростом

Модуляция импульсных носителей Передаваемый сигнал (сообщение) тем или иным способом изменяют вспомогательную импульсную последовательность, которая в свою очередь модулирует высокочастотное колебание

M

Модуляция импульсных носителей Первый вопрос: Выбор частоты следования импульсов ( «тактовая частота» ) Для улучшения использования радиолинии (повышения пропускной способности) выгодно увеличивать интервалы между импульсами, т. е. уменьшать F. Однако, уменьшение F ниже определенного минимума, зависящего от частотного спектра передаваемого сообщения недопустимо, т. к. приводит к потере информации

Модуляция импульсных носителей В соответствии с «Теоремой отсчетов» (теоремой Котельникова) из теории информации: Если наивысшая частота сообщений Fm, то интервалы между импульсами не должны превышать Тогда F должна удовлетворять условию:

Модуляция импульсных носителей АИМ – аплитудно-импульсная модуляция ЦИМ – частотно-импульсная модуляция (частота следования импульсов меняется в соответствии с амплитудой сообщений) ДИМ – импульсная модуляция по длительности (односторонняя и двусторонняя) Один или оба фронта импульса изменяются в процессе модуляции на величину t, пропорциональную модулирующему напряжению ВИМ – временная импульсная модуляция (тактовые импульсы, сохраняя свою форму и величину смешиваются u < , определенным образом связанную с напряжением модулирующего сигнала)

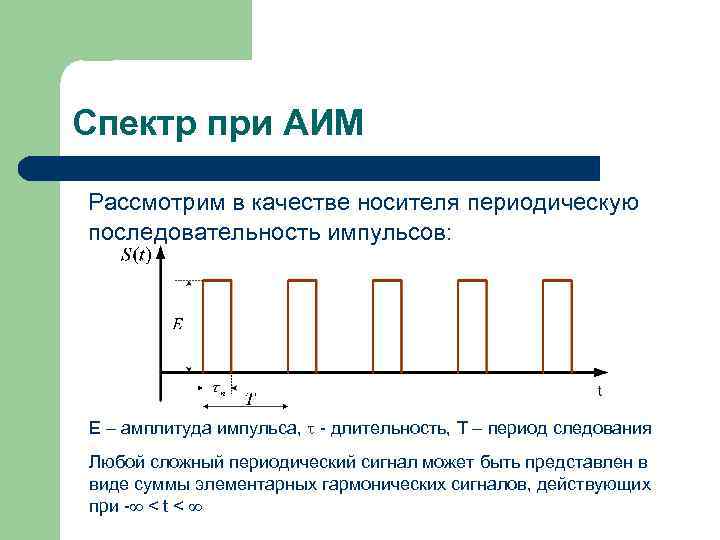Спектр при АИМ Рассмотрим в качестве носителя периодическую последовательность импульсов: E – амплитуда импульса, - длительность, T – период следования Любой сложный периодический сигнал может быть представлен в виде суммы элементарных гармонических сигналов, действующих при - < t <

Спектр при АИМ Это представление осуществляется в виде ряда Фурье:

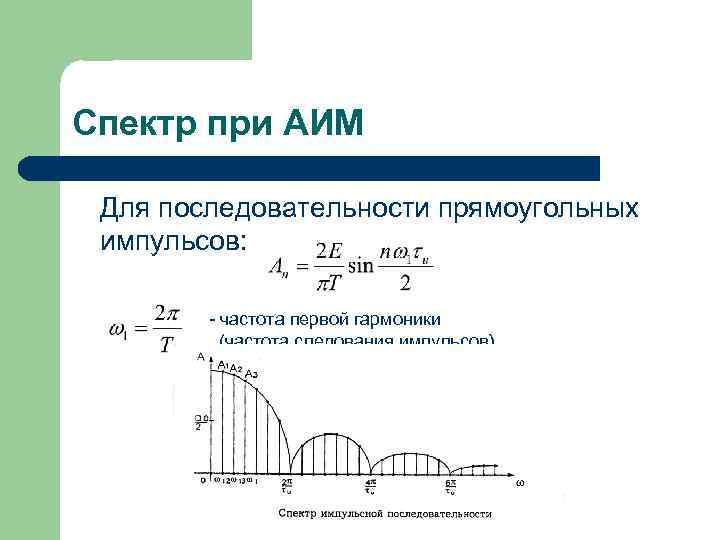Спектр при АИМ Для последовательности прямоугольных импульсов: - частота первой гармоники (частота следования импульсов)

Спектр при АИМ При АИМ В простейшем случае: или Получаем:

Спектр при АИМ Отсюда видно, что кроме основных линий, содержащихся в спектре носителя имеются дополнительные линии меньших размеров на частотах Вывод: Несмотря на то, что при модуляции носителя характер спектра меняется его ширина практически не изменяется Эта величина берется за основу при определении полосы пропускания системы передачи информации с импульсным носителем