Теория игр в экономике Лекция 1 -2 Введение

Теория игр в экономике Лекция 1 -2 Введение в теорию игр. 1. Основные определения

Основные определения • Определение 1. Пусть заданы множества Si , i = 1, 2, 3, …, n элементов, из которых игрок с номером i I может выбрать любой элемент xi Si. Любой элемент xi Si называется стратегией i –го игрока, а Si - множеством его стратегий. • Стратегия каждого игрока может быть многомерным набором чисел, при этом размерности у различных игроков могут быть различными.

Основные определения • Определение 2. Набор выбранных всеми игроками стратегий , т. е. набор называется ситуацией. • Множество всех ситуаций ( декартовое умножение) обозначается через и означает, что из каждого множества Si выбирается по одному элементу xi и составляется набор.

Основные определения • Определение 3. Пусть на множестве ситуаций определены n функций. Если число Hi (ŝ) означает сумму, которую получит i –ый игрок при ситуации , то называют функцией выигрыша i –го игрока.

Основные определения • Определение 4. Игрой называют процесс, при котором каждый из игроков в какой-то момент выбирает себе стратегию ив возникшей ситуации получает выигрыш. • Если задан набор , то говорят, что определена игра G, а сам набор G называют математической моделью игры или игрой G.

Основные определения • Пусть в игре G возникла ситуация. Тогда в этой ситуации каждый из игроков выигрывает Если же игрок под номером i заменит свою стратегию на стратегию , то возникнет ситуация , которую будем обозначать .

Основные определения • Определение 5. Ситуация называется приемлемой для i – го игрока, если • Определение 6. Ситуация называется решением игры или ситуацией равновесия, если она является приемлемой для всех игроков, т. е. если указанное выше условие выполняется для всех. Координата ситуации равновесия называется оптимальной стратегией i -го игрока.

Определение 6. Игра в нормальной форме задается следующей совокупностью объектов: где множество игроков множество стратегий игрока i функция выигрыша игрока i

Профиль стратегий всех игроков: Профиль стратегий всех игроков, кроме i – го (т. е. остальных игроков): При этом очевидно, что

Определение 7. Для игры в нормальной форме стратегия строго доминирует стратегию , если • (Строго) доминирующая стратегия (если она существует) (строго) доминирует любую другую стратегию данного игрока. • (Строго) доминируемая стратегия – это такая стратегия игрока, которую (строго) доминирует некоторая другая стратегия данного игрока

• Определение 8. Равновесием в (строго) доминирующих стратегиях называется профиль (строго) доминирующих стратегий, если такие стратегии существуют для каждого игрока.

• Задача теории игр —по данному описанию игры предсказать, какие стратегии выберут игроки и каким при этом будет исход игры, или, по крайней мере, сузить множество прогнозируемых исходов. • В некоторых случаях предсказать исход игры можно однозначно, если исходить из предположения о том, что каждый игрок рационален.

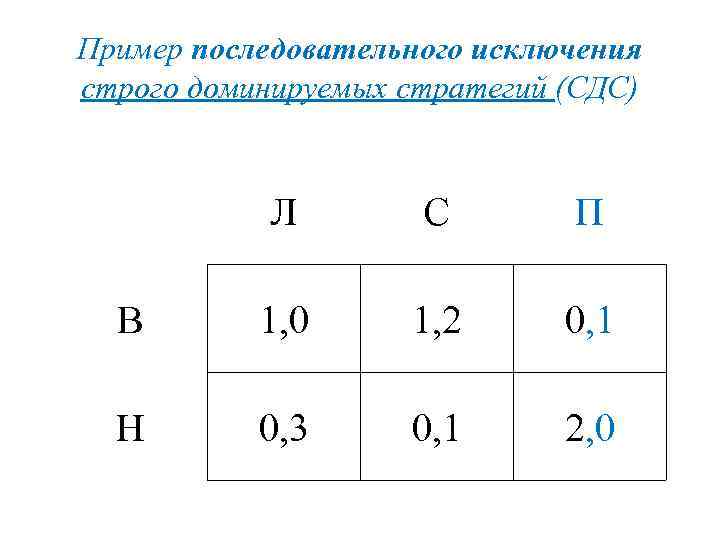Пример последовательного исключения строго доминируемых стратегий (СДС) Л С П В 1, 0 1, 2 0, 1 Н 0, 3 0, 1 2, 0

Пример последовательного исключения СДС. После исключения П: Л С В 1, 0 1, 2 Н 0, 3 0, 1

Пример последовательного исключения СДС. После исключения Н: Л В С 1, 0 1, 2 Стратегии , которые не отбрасываются при последовательном исключении СДС называют рационализируемыми.

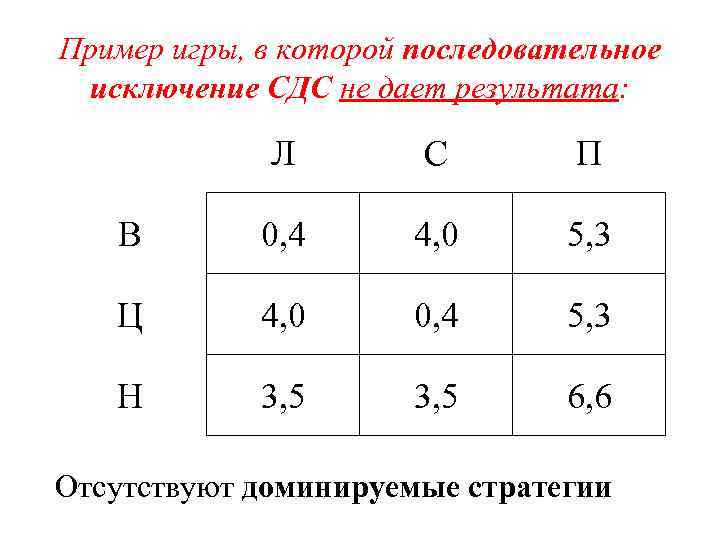Пример игры, в которой последовательное исключение СДС не дает результата: Л С П В 0, 4 4, 0 5, 3 Ц 4, 0 0, 4 5, 3 Н 3, 5 6, 6 Отсутствуют доминируемые стратегии

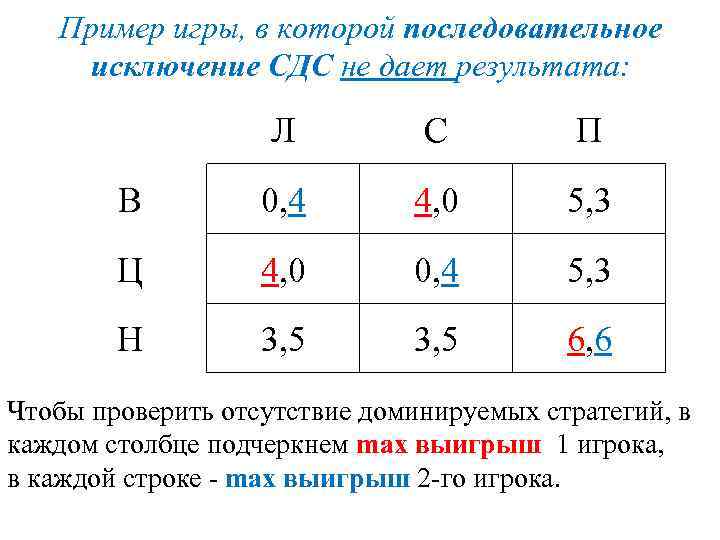Пример игры, в которой последовательное исключение СДС не дает результата: Л С П В 0, 4 4, 0 5, 3 Ц 4, 0 0, 4 5, 3 Н 3, 5 6, 6 Чтобы проверить отсутствие доминируемых стратегий, в каждом столбце подчеркнем max выигрыш 1 игрока, в каждой строке - max выигрыш 2 -го игрока.

Выводы • Всякая стратегия является наилучшей при некотором выборе другого игрока. • В этом случае подход, основанный на доминировании, бессилен, но напрашивается другой более универсальный подход.

Основные определения Определение 9. Равновесием Нэша (РН) в игре в нормальной форме называется такой профиль стратегий s* всех игроков, что: Отличие РН от доминирования состоит в том, что в РН стратегия игрока должна быть «хорошей» только в ответ на равновесные стратегии остальных игроков.

Определение 10. Отображение отклика i – го игрока сопоставляет каждому набору стратегий других игроков множество стратегий i-го игрока, каждая из которых является наилучшим ответом на s-i. Каждая стратегия такова, что Определение РН через отображение отклика: s* - РН, если В случае, если отображение отклика является функцией:

Пример. Для последней игры функции отклика такие: для первого игрока - на действия второго для второго игрока - на действия первого В Ц Н Л С П 0, 4 4, 0 5, 3 4, 0 0, 4 5, 3 3, 5 6, 6

Другой пример – «Дилемма заключенного» . Здесь функции отклика такие: для первого игрока - на действия второго для второго игрока - на действия первого М С М -1, -1 -9, 0 С 0, -9 -6, -6 В данном случае стратегия СС также является РН, как и любое равновесие в доминирующих стратегиях

«Семейный спор» • Молодые супруги хотят вместе провести вечер. Муж (игрок 1) хочет пойти на бокс, а жена (игрок 2) хочет послушать оперу. Муж, вообще говоря, готов и оперу послушать, но бокс любит больше. Жена могла бы пойти на бокс, но предпочитает оперу. По каким – то причинам (например, испортилась мобильная связь) они должны ехать к месту встречи без предварительной договоренности. Если они не встретятся, то это будет огорчением для обоих.

Нормальная форма игры имеет вид: Б О Б 2, 1 0, 0 О 0, 0 1, 2

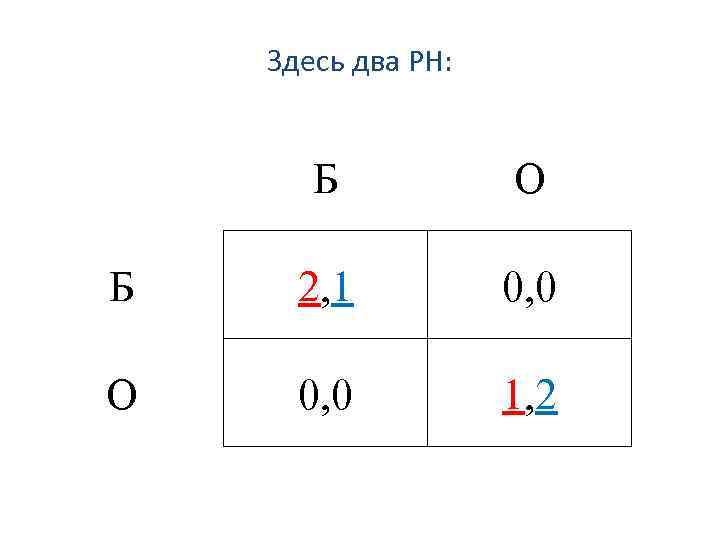Здесь два РН: Б О Б 2, 1 0, 0 О 0, 0 1, 2

Утверждение 1. Пусть в игре в нормальной форме последовательное исключение СДС приводит к единственному профилю стратегий s*, тогда s* является единственным РН в данной игре. Доказать! Утверждение 2. Пусть в игре в нормальной форме профиль стратегий s* является РН. Тогда стратегии si* не могут быть отброшены при последовательном исключении СДС. Доказать!

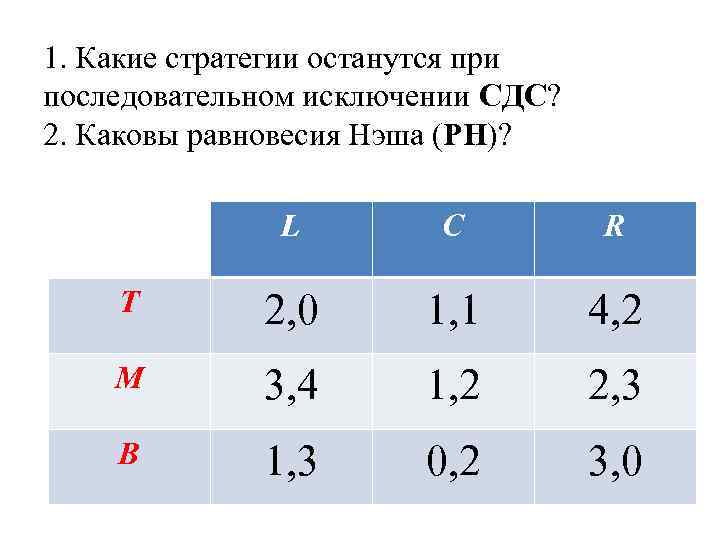1. Какие стратегии останутся при последовательном исключении СДС? 2. Каковы равновесия Нэша (РН)? L C R T 2, 0 1, 1 4, 2 M 3, 4 1, 2 2, 3 B 1, 3 0, 2 3, 0