 Теория игр и олигополия
Теория игр и олигополия
 Теория игр и олигополия • • Теория игр была основана Джоном фон Нейманом (1903 -1957) и Оскаром Моргенштерном (1901 -1977) в их первой работе “The Theory of Games and Economic Behavior”, изданной в 1944 году. В 1928 году в «Математических анналах» фон Нейманом была опубликована статья “О теории общественных игр” в которой впервые было применено понятие “теория игр”. Использование этого понятия объясняется схожестью логики принятия решений в таких играх, как шахматы, скат или покер, и в некоторых ситуациях общественной жизни, прежде всего в экономике и военном деле. Характерным для таких ситуаций является то, что результат для принимающего решение зависит не только от его решения, но и от того, какое решение примут другие. Поэтому оптимальный исход не может быть получен в результате принятия решения одним лицом. •
Теория игр и олигополия • • Теория игр была основана Джоном фон Нейманом (1903 -1957) и Оскаром Моргенштерном (1901 -1977) в их первой работе “The Theory of Games and Economic Behavior”, изданной в 1944 году. В 1928 году в «Математических анналах» фон Нейманом была опубликована статья “О теории общественных игр” в которой впервые было применено понятие “теория игр”. Использование этого понятия объясняется схожестью логики принятия решений в таких играх, как шахматы, скат или покер, и в некоторых ситуациях общественной жизни, прежде всего в экономике и военном деле. Характерным для таких ситуаций является то, что результат для принимающего решение зависит не только от его решения, но и от того, какое решение примут другие. Поэтому оптимальный исход не может быть получен в результате принятия решения одним лицом. •
 Виды игр • 1. Представление игры в развернутой и в нормальной форме • 2. Некооперативная игра с двумя участниками и нулевой суммой выигрыша • 3. Некооперативная игра с двумя участниками и ненулевой суммой выигрыша • 4. Динамические игры • 5. Эволюционные игры
Виды игр • 1. Представление игры в развернутой и в нормальной форме • 2. Некооперативная игра с двумя участниками и нулевой суммой выигрыша • 3. Некооперативная игра с двумя участниками и ненулевой суммой выигрыша • 4. Динамические игры • 5. Эволюционные игры
 • • • Представление игры в развернутой и в нормальной форме Развернутая форма Игра может быть представлена как совокупность всех возможных ходов и выплат (выигрышей). Пример: Игра со спичками На столе лежат 6 спичек. 2 игрока по очереди берут по одной или по две спички. Тот, кто возьмет последним 1 или 2 спички, тот победил. Игру можно представить в виде следующего дерева игры:
• • • Представление игры в развернутой и в нормальной форме Развернутая форма Игра может быть представлена как совокупность всех возможных ходов и выплат (выигрышей). Пример: Игра со спичками На столе лежат 6 спичек. 2 игрока по очереди берут по одной или по две спички. Тот, кто возьмет последним 1 или 2 спички, тот победил. Игру можно представить в виде следующего дерева игры:
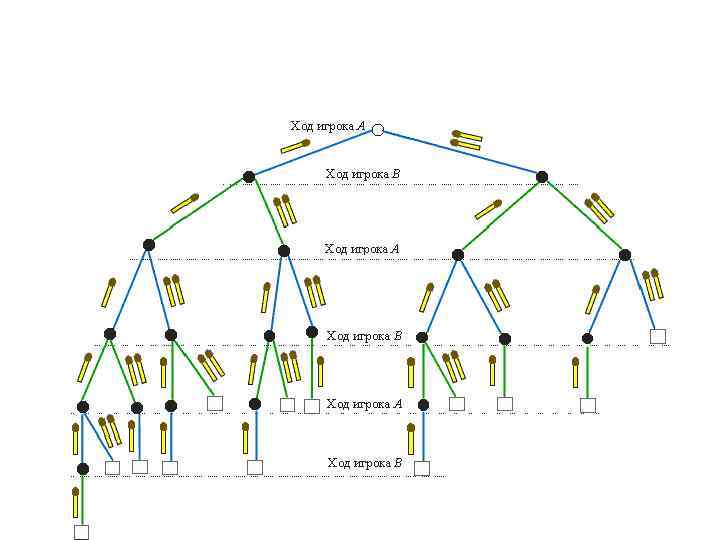
 • Это развернутая форма представления игры. Каждому конечному пункту, отмеченному квадратиком, соответствует один исход игры. В этой игре возможны 13 исходов. Представим в качестве примера по одной из стратегий каждого игрока. • Примечание: пунктирные линии обозначают возможные, но не используемые в данной стратегии ходы игрока.
• Это развернутая форма представления игры. Каждому конечному пункту, отмеченному квадратиком, соответствует один исход игры. В этой игре возможны 13 исходов. Представим в качестве примера по одной из стратегий каждого игрока. • Примечание: пунктирные линии обозначают возможные, но не используемые в данной стратегии ходы игрока.
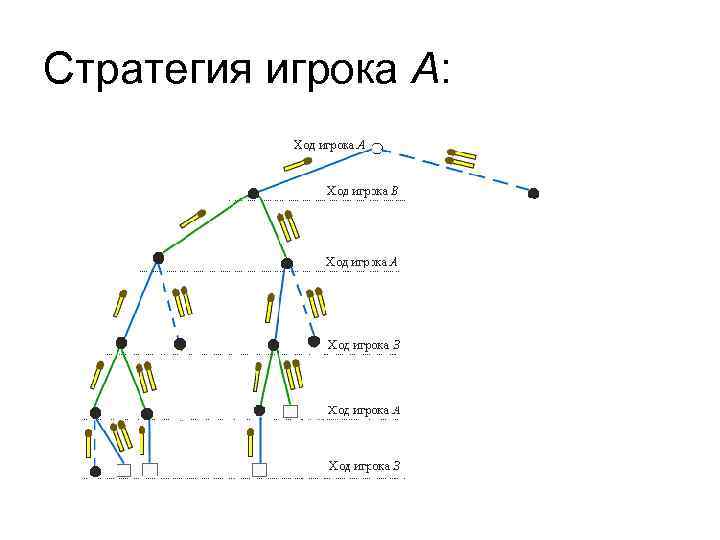 Стратегия игрока А:
Стратегия игрока А:
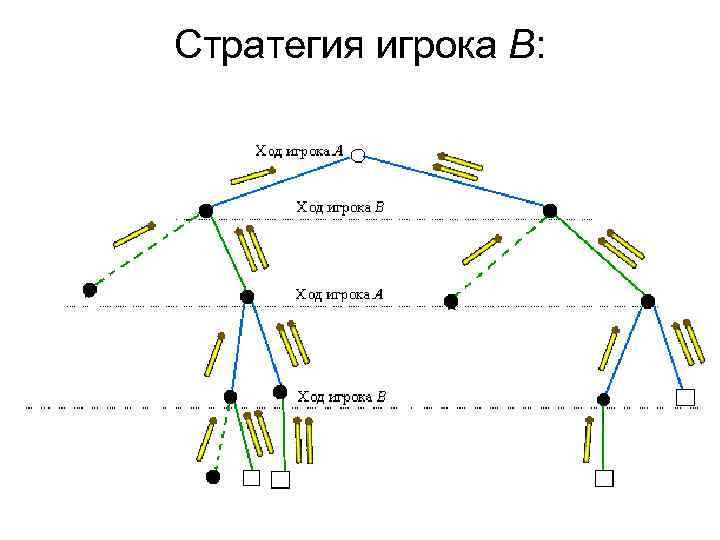 Стратегия игрока В:
Стратегия игрока В:
 Таблица 1 Стратегии игрока В b 2 . . . bj . . . bn a 1 x 11; y 11 x 12; y 12 . . . x 1 j; y 1 j . . . x 1 n; y 1 n a 2 Стратегии игрока А b 1 x 21; y 21 x 22; y 22 . . . x 2 j; y 2 j . . . x 2 n; y 2 n . . ai . . xij; yij . . . . am xm 1; ym 1 xm 2; ym 2 . . . xmj; ymj . . . xmn; ymn
Таблица 1 Стратегии игрока В b 2 . . . bj . . . bn a 1 x 11; y 11 x 12; y 12 . . . x 1 j; y 1 j . . . x 1 n; y 1 n a 2 Стратегии игрока А b 1 x 21; y 21 x 22; y 22 . . . x 2 j; y 2 j . . . x 2 n; y 2 n . . ai . . xij; yij . . . . am xm 1; ym 1 xm 2; ym 2 . . . xmj; ymj . . . xmn; ymn
 • ai – стратегии игрока А; bj – стратегии игрока B; xij – выплаты игроку А от игрока В при сочетании стратегий ai и bj; yij – выплаты игроку В от игрока А при сочетании стратегий ai и bj; • По условию оба игрока знают все параметры платежной матрицы и каждый определяет свою стратегию независимо друг от друга. Вопрос: существует ли в этих условиях оптимальная для каждого из игроков стратегия?
• ai – стратегии игрока А; bj – стратегии игрока B; xij – выплаты игроку А от игрока В при сочетании стратегий ai и bj; yij – выплаты игроку В от игрока А при сочетании стратегий ai и bj; • По условию оба игрока знают все параметры платежной матрицы и каждый определяет свою стратегию независимо друг от друга. Вопрос: существует ли в этих условиях оптимальная для каждого из игроков стратегия?
 Некооперативная игра с двумя участниками и нулевой суммой выигрыша • Поскольку xij + yij = 0, то yij = –xij и поэтому в платежной матрице можно оставить только xij , полагая, что при xij > 0 игрок В платит игроку А, а при xij < 0 игрок А платит игроку В. Тогда платежная матрица принимает вид табл. 2.
Некооперативная игра с двумя участниками и нулевой суммой выигрыша • Поскольку xij + yij = 0, то yij = –xij и поэтому в платежной матрице можно оставить только xij , полагая, что при xij > 0 игрок В платит игроку А, а при xij < 0 игрок А платит игроку В. Тогда платежная матрица принимает вид табл. 2.
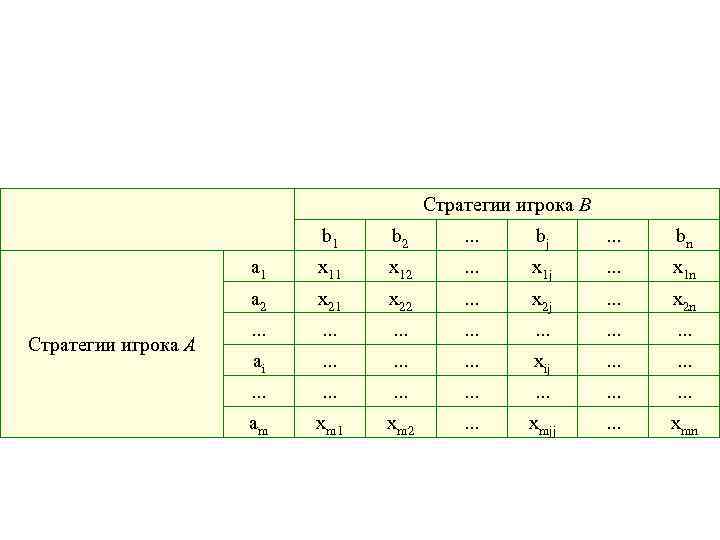 Стратегии игрока В b 2 . . . bj . . . bn a 1 x 12 . . . x 1 j . . . x 1 n a 2 Стратегии игрока А b 1 x 22 . . . x 2 j . . . x 2 n . . ai . . xij . . . . am xm 1 xm 2 . . . xmjj . . . xmn
Стратегии игрока В b 2 . . . bj . . . bn a 1 x 12 . . . x 1 j . . . x 1 n a 2 Стратегии игрока А b 1 x 22 . . . x 2 j . . . x 2 n . . ai . . xij . . . . am xm 1 xm 2 . . . xmjj . . . xmn
 • В такой игре имеет место полный конфликт интересов. Поэтому каждый игрок считает, что соперник выберет наихудшую для него (игрока) стратегию. Для принятия решения игрок А в каждой строке находит минимум и из образовавшегося столбца минимумов выбирает максимальное значение. Аналогично игрок В (поскольку xij представляют его выплаты игроку А) в каждой строке находит максимум и из образовавшегося строки максимумов выбирает минимальное значение. Такое поведение игроков получило название поведение по критерию maximin. Оно крайне пессимистично.
• В такой игре имеет место полный конфликт интересов. Поэтому каждый игрок считает, что соперник выберет наихудшую для него (игрока) стратегию. Для принятия решения игрок А в каждой строке находит минимум и из образовавшегося столбца минимумов выбирает максимальное значение. Аналогично игрок В (поскольку xij представляют его выплаты игроку А) в каждой строке находит максимум и из образовавшегося строки максимумов выбирает минимальное значение. Такое поведение игроков получило название поведение по критерию maximin. Оно крайне пессимистично.
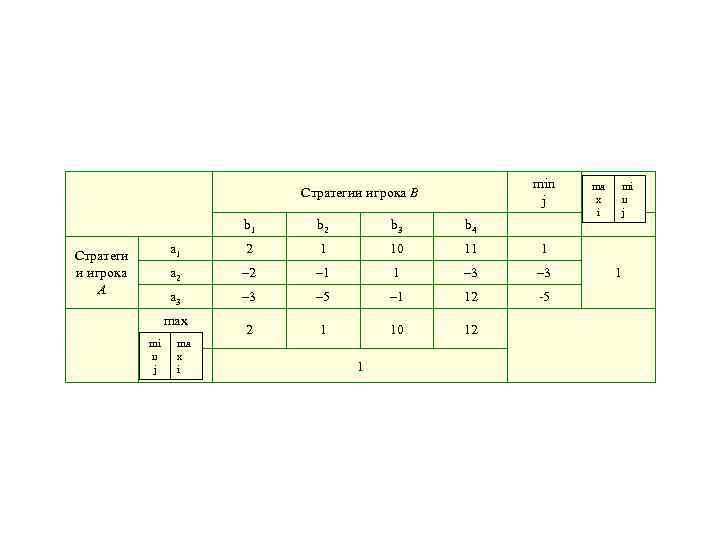 min j Стратегии игрока В b 1 b 3 b 4 a 1 2 1 10 11 1 a 2 – 1 1 – 3 a 3 Стратеги и игрока А b 2 – 3 – 5 – 1 12 -5 2 1 10 12 max mi ima n j ma x i 1 1 mi n j
min j Стратегии игрока В b 1 b 3 b 4 a 1 2 1 10 11 1 a 2 – 1 1 – 3 a 3 Стратеги и игрока А b 2 – 3 – 5 – 1 12 -5 2 1 10 12 max mi ima n j ma x i 1 1 mi n j
 • Выбирая стратегию b 2, игрок В гарантирует себе, что при любом исходе ему не придется платить больше 1. В свою очередь, игрок А, выбирая стратегию a 1, может быть уверен, что получит не меньше 1. В рассматриваемом примере для игрока А стратегия a 1 доминирует над стратегией a 2, так как при любом поведении игрока В стратегия a 1 обеспечивает ему больший выигрыш, чем стратегия a 2.
• Выбирая стратегию b 2, игрок В гарантирует себе, что при любом исходе ему не придется платить больше 1. В свою очередь, игрок А, выбирая стратегию a 1, может быть уверен, что получит не меньше 1. В рассматриваемом примере для игрока А стратегия a 1 доминирует над стратегией a 2, так как при любом поведении игрока В стратегия a 1 обеспечивает ему больший выигрыш, чем стратегия a 2.
 • Из аналогичных рассуждений следует, что для игрока В стратегия b 2 доминирует над стратегией b 3; при выборе стратегии b 2 все его возможные выплаты игроку А меньше (соответственно, В получает от А больше), чем при выборе стратегии b 3. Следовательно, игрок А никогда не выберет стратегию a 2, а игрок В стратегию b 3. Удалив из платежной матрицы доминирующие стратегии, получим табл. 3 b.
• Из аналогичных рассуждений следует, что для игрока В стратегия b 2 доминирует над стратегией b 3; при выборе стратегии b 2 все его возможные выплаты игроку А меньше (соответственно, В получает от А больше), чем при выборе стратегии b 3. Следовательно, игрок А никогда не выберет стратегию a 2, а игрок В стратегию b 3. Удалив из платежной матрицы доминирующие стратегии, получим табл. 3 b.
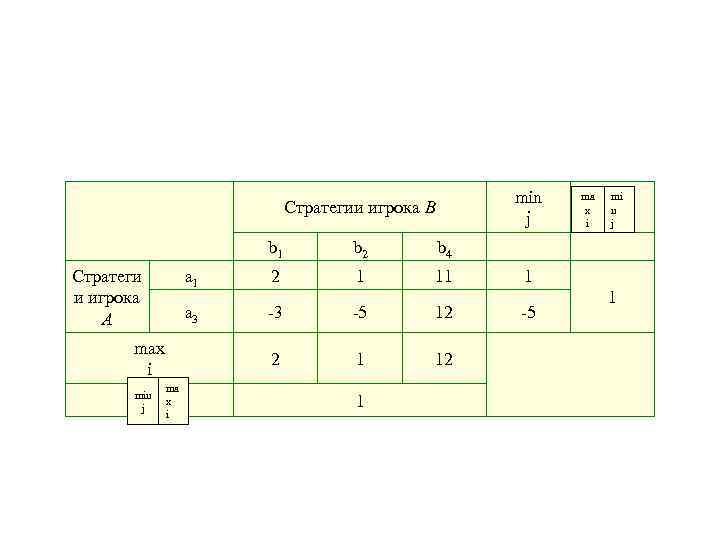 min j Стратегии игрока В b 1 min j 2 1 11 -3 -5 12 1 12 mi n j 1 2 ma x i a 3 max i b 4 a 1 Стратеги и игрока А b 2 ma x i 1 1 -5
min j Стратегии игрока В b 1 min j 2 1 11 -3 -5 12 1 12 mi n j 1 2 ma x i a 3 max i b 4 a 1 Стратеги и игрока А b 2 ma x i 1 1 -5
 • Пара стратегий (a*, b*), обеспечивающая равенство называется седловым решением игры. Решение maximin может быть только в некооперативной игре с двумя участниками и нулевой (постоянной) суммой выигрыша.
• Пара стратегий (a*, b*), обеспечивающая равенство называется седловым решением игры. Решение maximin может быть только в некооперативной игре с двумя участниками и нулевой (постоянной) суммой выигрыша.
 • Для игры с двумя участниками и нулевой суммой выигрыша верна следующая теорема (теорема minimaxa): где f(ai, bj) - величина выплаты игрока В игроку А при выборе стратегий ai, bj.
• Для игры с двумя участниками и нулевой суммой выигрыша верна следующая теорема (теорема minimaxa): где f(ai, bj) - величина выплаты игрока В игроку А при выборе стратегий ai, bj.
 • Левая часть этого неравенства означает, что игрок А может себе гарантировать получение от игрока В по меньшей мере • Правая часть означает, что игрок В может себе гарантировать, что ему не придется платить больше, чем
• Левая часть этого неравенства означает, что игрок А может себе гарантировать получение от игрока В по меньшей мере • Правая часть означает, что игрок В может себе гарантировать, что ему не придется платить больше, чем
 • Вербально теорема минимакса звучит так: игрок А не может гарантировать себе больше максимума всевозможных выплат игрока В.
• Вербально теорема минимакса звучит так: игрок А не может гарантировать себе больше максимума всевозможных выплат игрока В.
 • Доказательство: Допустим, две любые стратегии. • Тогда и • Отсюда следует: . • Поскольку и любые стратегии, то должно быть:
• Доказательство: Допустим, две любые стратегии. • Тогда и • Отсюда следует: . • Поскольку и любые стратегии, то должно быть:

 • Из теоремы minimaxa можно вывести следующие правила рационального поведения в некооперативной игре с двумя участниками и нулевой суммой выигрыша: • при полном противоречии интересов игроков, не зная стратегии поведения противника, разумно выбирать решение седловой точки; • если известно, что противник не придерживается стратегии, соответствующей седловой точке, то самому тоже не нужно придерживаться этой такой стратегии; • Даже если известно, что соперник выбирает свою стратегию седловой точки, то целесообразно выбрать стратегию седловой точки. Т. е. лучшим ответом на стратегию седловой точки соперника, является собственная стратегия седловой точки.
• Из теоремы minimaxa можно вывести следующие правила рационального поведения в некооперативной игре с двумя участниками и нулевой суммой выигрыша: • при полном противоречии интересов игроков, не зная стратегии поведения противника, разумно выбирать решение седловой точки; • если известно, что противник не придерживается стратегии, соответствующей седловой точке, то самому тоже не нужно придерживаться этой такой стратегии; • Даже если известно, что соперник выбирает свою стратегию седловой точки, то целесообразно выбрать стратегию седловой точки. Т. е. лучшим ответом на стратегию седловой точки соперника, является собственная стратегия седловой точки.
 • Так как это верно одновременно для обоих игроков, то решение седловой точки называют также равновесным решением некооперативной игры с двумя участниками и нулевой суммой выигрыша. • Это понятие равновесия можно обобщить. Под некооперативным равновесием понимается пара стратегий , • которые выбраны независимо друг от друга и сохраняются обоими игроками до тех пор пока кто-то из них изменит свою стратегию. Такое равновесие называется также равновесием Нэша, так как он первым описал такое решение (Nash J. F. Non. Cooperative Games // Annals of Mathematics. (54) 1951, p. 286 -295).
• Так как это верно одновременно для обоих игроков, то решение седловой точки называют также равновесным решением некооперативной игры с двумя участниками и нулевой суммой выигрыша. • Это понятие равновесия можно обобщить. Под некооперативным равновесием понимается пара стратегий , • которые выбраны независимо друг от друга и сохраняются обоими игроками до тех пор пока кто-то из них изменит свою стратегию. Такое равновесие называется также равновесием Нэша, так как он первым описал такое решение (Nash J. F. Non. Cooperative Games // Annals of Mathematics. (54) 1951, p. 286 -295).
 • В общей форме равновесие Нэша можно сформулировать следующим образом: ни один из игроков не может улучшить своего положения путем отклонения от стратегии равновесия, если остальные игроки останутся при стратегии равновесия.
• В общей форме равновесие Нэша можно сформулировать следующим образом: ни один из игроков не может улучшить своего положения путем отклонения от стратегии равновесия, если остальные игроки останутся при стратегии равновесия.
 Некооперативная игра с двумя участниками и ненулевой суммой выигрыша • Эти игры отличаются от предыдущих тем, что , • т. е. выигрыш одного игрока не равен проигрышу другого. Кооперация между игроками была бы целесообразна, но либо невозможна, либо запрещена (закон о картелях).
Некооперативная игра с двумя участниками и ненулевой суммой выигрыша • Эти игры отличаются от предыдущих тем, что , • т. е. выигрыш одного игрока не равен проигрышу другого. Кооперация между игроками была бы целесообразна, но либо невозможна, либо запрещена (закон о картелях).
 • Дилемма заключенного. Такая ситуация может быть рассмотрена на примере известной дилеммы заключенных. Двое заключенных A и B, задержанные полицией, допрашиваются отдельно друг от друга. Если оба признаются в совершенном преступлении, то оба будут лишены свободы на срок в 10 лет. Если оба будут отрицать свое участие в преступлении, то улик будет достаточно лишь для приговора к 2 годам лишения свободы. Если же признается только один заключенный, то он станет свидетелем по делу и будет освобожден, в то время как его соучастник будет заключен на 20 лет. Эти обстоятельства известны обоим. Каким же образом им следует себя вести?
• Дилемма заключенного. Такая ситуация может быть рассмотрена на примере известной дилеммы заключенных. Двое заключенных A и B, задержанные полицией, допрашиваются отдельно друг от друга. Если оба признаются в совершенном преступлении, то оба будут лишены свободы на срок в 10 лет. Если оба будут отрицать свое участие в преступлении, то улик будет достаточно лишь для приговора к 2 годам лишения свободы. Если же признается только один заключенный, то он станет свидетелем по делу и будет освобожден, в то время как его соучастник будет заключен на 20 лет. Эти обстоятельства известны обоим. Каким же образом им следует себя вести?
 • Изложенная ситуация представлена внизу в виде табл. 4. Числа указывают сроки заключения в годах, при этом первая относится к заключенному A, вторая – к B.
• Изложенная ситуация представлена внизу в виде табл. 4. Числа указывают сроки заключения в годах, при этом первая относится к заключенному A, вторая – к B.
 B Непризнание А Признание Непризнан ие 2; 2 20; 0 Признание 0; 20 10; 10
B Непризнание А Признание Непризнан ие 2; 2 20; 0 Признание 0; 20 10; 10
 • Заключенный A оценивает данную ситуацию следующим образом. Независимо от решения B, A находится в более выгодном положении, если он решит признаться, так как, если B тоже признается, то A будет лишен свободы на 10 лет, вместо 20, (в том случае, если A не признается). Если же B не признается, то A будет освобожден вместо лишения свободы на 2 года в случае непризнания. Руководствуясь личной рациональностью, A принимает решение признать свою вину.
• Заключенный A оценивает данную ситуацию следующим образом. Независимо от решения B, A находится в более выгодном положении, если он решит признаться, так как, если B тоже признается, то A будет лишен свободы на 10 лет, вместо 20, (в том случае, если A не признается). Если же B не признается, то A будет освобожден вместо лишения свободы на 2 года в случае непризнания. Руководствуясь личной рациональностью, A принимает решение признать свою вину.
 • • • На основе аналогичных рассуждений заключенный B также признается. В результате оба будут заключены на 10 лет. Обратим внимание на то, что в рассматриваемом случае индивидуальная рациональность поведения не совпадает с коллективной рациональностью: если бы оба отрицали свою причастность к преступлению, то получили бы лишь по 2 года тюрьмы Допустим, что оба заключенных перед задержанием договорились о том, что оба не будут признаваться, т. е. поведут себя в соответствии с коллективной рациональностью. Тогда возникает следующая проблема. Теперь каждый из заключенных, полагая, что его напарник будет отрицать свое участие в преступлении, захочет признаться, чтобы выйти из тюрьмы. В результате оба признаются и получат по 10 лет заключения. Различные варианты равновесия Нэша играют в теории игр большую роль. Для их иллюстрации рассмотрим пример из экономики.
• • • На основе аналогичных рассуждений заключенный B также признается. В результате оба будут заключены на 10 лет. Обратим внимание на то, что в рассматриваемом случае индивидуальная рациональность поведения не совпадает с коллективной рациональностью: если бы оба отрицали свою причастность к преступлению, то получили бы лишь по 2 года тюрьмы Допустим, что оба заключенных перед задержанием договорились о том, что оба не будут признаваться, т. е. поведут себя в соответствии с коллективной рациональностью. Тогда возникает следующая проблема. Теперь каждый из заключенных, полагая, что его напарник будет отрицать свое участие в преступлении, захочет признаться, чтобы выйти из тюрьмы. В результате оба признаются и получат по 10 лет заключения. Различные варианты равновесия Нэша играют в теории игр большую роль. Для их иллюстрации рассмотрим пример из экономики.
 Динамические игры • • • До сих пор были рассмотрены игры, которые играются однократно или каждый из игроков выбирал свою стратегию однократно. В тоже время существуют игры, в которых партии повторяются. Даже, если в части игры присутствует оптимальное равновесие Нэша, у игрока тем не менее возникает вопрос выбора стратегии в соответствии со стратегиями игроков в прошлых и будущих играх. В дилемме заключенных эта проблема выгладит так: оба игрока кооперируют в первой партии игры, придерживаясь своей доминантной стратегии, и таким образом они оба выигрывают. Игрок 2 ожидает поэтому, что в следующей партии игрок 1 вновь будет кооперировать и выбирает поэтому для следующей партии вновь стратегию кооперации. Игрок 1 ожидая такое поведение игрока 2 выбирает для следующей игры стратегию некооперирования, т. е. обманывает игрока 2. Таким образом, игрок 1 получает более высокую сумму платежа, чем при стратегии кооперирования. В третьей партии игрок 2 может попробовать “отомстить” и не кооперировать и т. д. Игроки оказываются перед проблемой выбора стратегии кооперации или не кооперации и ритма смены стратегий.
Динамические игры • • • До сих пор были рассмотрены игры, которые играются однократно или каждый из игроков выбирал свою стратегию однократно. В тоже время существуют игры, в которых партии повторяются. Даже, если в части игры присутствует оптимальное равновесие Нэша, у игрока тем не менее возникает вопрос выбора стратегии в соответствии со стратегиями игроков в прошлых и будущих играх. В дилемме заключенных эта проблема выгладит так: оба игрока кооперируют в первой партии игры, придерживаясь своей доминантной стратегии, и таким образом они оба выигрывают. Игрок 2 ожидает поэтому, что в следующей партии игрок 1 вновь будет кооперировать и выбирает поэтому для следующей партии вновь стратегию кооперации. Игрок 1 ожидая такое поведение игрока 2 выбирает для следующей игры стратегию некооперирования, т. е. обманывает игрока 2. Таким образом, игрок 1 получает более высокую сумму платежа, чем при стратегии кооперирования. В третьей партии игрок 2 может попробовать “отомстить” и не кооперировать и т. д. Игроки оказываются перед проблемой выбора стратегии кооперации или не кооперации и ритма смены стратегий.
 Конечное число партий • Рассмотрим игру с частичным равновесием Нэша с конечным количеством партий, которое знакомо игрокам. В данном случае для каждого из игроков будет рациональным в последней партии играть в соответствии со стратегией Нэша, т. е. не кооперировать, так как более не будет партий, в которых другой игрок мог бы “отомстить”. В последней партии, т. о. , все игроки не будут кооперировать. • Поэтому для всех игроков также выгоднее не кооперировать уже в предпоследней игре, так, как в последней партии последует “отмщение” со стороны другого игрока. С помощью индуктивного метода можно прийти к заключению, что все игроки не будут кооперировать уже в первой партии, т. е. во всех партиях будет применяться стратегия равновесия Нэша.
Конечное число партий • Рассмотрим игру с частичным равновесием Нэша с конечным количеством партий, которое знакомо игрокам. В данном случае для каждого из игроков будет рациональным в последней партии играть в соответствии со стратегией Нэша, т. е. не кооперировать, так как более не будет партий, в которых другой игрок мог бы “отомстить”. В последней партии, т. о. , все игроки не будут кооперировать. • Поэтому для всех игроков также выгоднее не кооперировать уже в предпоследней игре, так, как в последней партии последует “отмщение” со стороны другого игрока. С помощью индуктивного метода можно прийти к заключению, что все игроки не будут кооперировать уже в первой партии, т. е. во всех партиях будет применяться стратегия равновесия Нэша.
 Бесконечное число партий • Аргументация, приведенная выше, не может быть применена при бесконечном числе партий игры или в случае, если число партий ограничено, но неизвестно игрокам. Как в таком случае будет выглядеть оптимальная стратегия игроков? Роберт Аксельрод проводил компьютерные имитации для представленной ниже ситуации, соответствующей дилемме заключенных.
Бесконечное число партий • Аргументация, приведенная выше, не может быть применена при бесконечном числе партий игры или в случае, если число партий ограничено, но неизвестно игрокам. Как в таком случае будет выглядеть оптимальная стратегия игроков? Роберт Аксельрод проводил компьютерные имитации для представленной ниже ситуации, соответствующей дилемме заключенных.
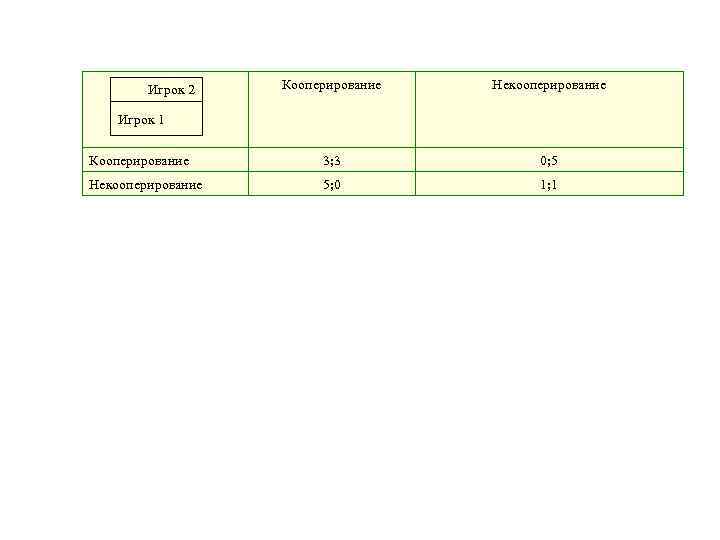 Кооперирование Некооперирование Кооперирование 3; 3 0; 5 Некооперирование 5; 0 1; 1 Игрок 2 Игрок 1
Кооперирование Некооперирование Кооперирование 3; 3 0; 5 Некооперирование 5; 0 1; 1 Игрок 2 Игрок 1
 • Он переписывался с ведущими специалистами по теории игр и просил их определить оптимальные стратегии для игры состоящей из нескольких партий, число которых неизвестно. Кроме того, Аксельрод получил множество стратегий от психологов, экономистов, политологов, математиков и социологов. Он проигрывал для каждой из стратегий 200 партий с помощью имитационной программы, причем каждая из стратегий играла против всех других и против самой себя. Победителем стала стратегия Tit-for-Tat, которую предложил A. Рапопорт.
• Он переписывался с ведущими специалистами по теории игр и просил их определить оптимальные стратегии для игры состоящей из нескольких партий, число которых неизвестно. Кроме того, Аксельрод получил множество стратегий от психологов, экономистов, политологов, математиков и социологов. Он проигрывал для каждой из стратегий 200 партий с помощью имитационной программы, причем каждая из стратегий играла против всех других и против самой себя. Победителем стала стратегия Tit-for-Tat, которую предложил A. Рапопорт.
 Эволюционные игры • До сих пор исходили из того, что игроки – рационально думающие люди, которые способны определять свое поведение автономно. Интересно отметить, что концепция теории игр используется в биологии, где они помогли понять развитие популяций животных. Конечно же, животные определяют характер своего поведения, не осознавая того, что находятся в ситуации, в которой результат принимаемого решения зависит также от автономно принимаемых решений других игроков. Поэтому в эволюционных играх каждая стратегия идентифицируется с одним игроком: при наличии n стратегий должны также присутствовать n игроков, представляющих данные стратегии.
Эволюционные игры • До сих пор исходили из того, что игроки – рационально думающие люди, которые способны определять свое поведение автономно. Интересно отметить, что концепция теории игр используется в биологии, где они помогли понять развитие популяций животных. Конечно же, животные определяют характер своего поведения, не осознавая того, что находятся в ситуации, в которой результат принимаемого решения зависит также от автономно принимаемых решений других игроков. Поэтому в эволюционных играх каждая стратегия идентифицируется с одним игроком: при наличии n стратегий должны также присутствовать n игроков, представляющих данные стратегии.
 • • • Выплаты в игре в данном случае выступают в виде выживаемости биологического вида, которая выражается через увеличение его популяции: определенный вид животных увеличивается. Основополагающим для подобных эволюционных игр является концепция “стабильной эволюционной стратегии”. Проще говоря, стратегия стабильна тогда, когда при появлении в популяции мутантов выживаемость последних ниже выживаемости чистокровных экземпляров. Мутанты в таком случае вымирают, тем самым не внеся изменений в популяцию. Эта концепция может быть применена для различных популяций, как показано ниже в примере. В закрытом анклаве с одним источником воды живут соколы и голуби. Оба вида птиц вынуждены пользоваться этим источником. Если у источника встречаются два голубя, то оба мирно пьют из него. Если у воды оказываются сокол с голубем, то первый прогоняет второго и пьет один. Если же у водоема встретятся 2 сокола то они начнут драться и в результате останутся оба без питья. Эта ситуация представлена в таблице ниже
• • • Выплаты в игре в данном случае выступают в виде выживаемости биологического вида, которая выражается через увеличение его популяции: определенный вид животных увеличивается. Основополагающим для подобных эволюционных игр является концепция “стабильной эволюционной стратегии”. Проще говоря, стратегия стабильна тогда, когда при появлении в популяции мутантов выживаемость последних ниже выживаемости чистокровных экземпляров. Мутанты в таком случае вымирают, тем самым не внеся изменений в популяцию. Эта концепция может быть применена для различных популяций, как показано ниже в примере. В закрытом анклаве с одним источником воды живут соколы и голуби. Оба вида птиц вынуждены пользоваться этим источником. Если у источника встречаются два голубя, то оба мирно пьют из него. Если у воды оказываются сокол с голубем, то первый прогоняет второго и пьет один. Если же у водоема встретятся 2 сокола то они начнут драться и в результате останутся оба без питья. Эта ситуация представлена в таблице ниже
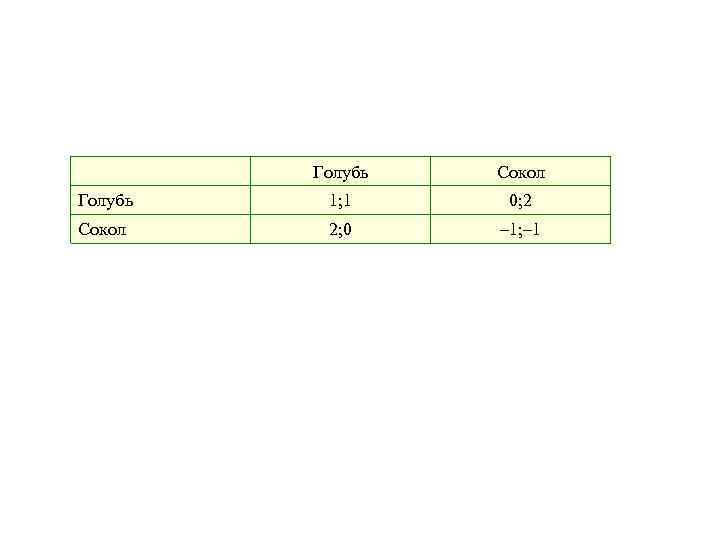 Голубь Сокол Голубь 1; 1 0; 2 Сокол 2; 0 – 1; – 1
Голубь Сокол Голубь 1; 1 0; 2 Сокол 2; 0 – 1; – 1
 • Числа в этой таблице обозначают выживаемость соответствующих видов птиц при встрече друг с другом. Если в начале игры обе популяции имеют одинаковое количество особей, то вероятность того, что голубь встретит другого голубя или сокола составляет в обоих случаях 0, 5. Среднее значение выживаемости голубя составит 0, 5· 1 + 0, 5· 0 = 0, 5, а для сокола 0, 5· 2 + 0, 5·(– 1) = 0, 5. • Так как в этом случае оба вида птиц имеют одинаковое значение выживаемости, то соотношение их численности со временем не изменится. Если этой игре с помощью дифференциальных уравнений придать динамику, то окажется, что популяции обоих видов птиц одинаковой величины стабильны по численности; если же в результате какого-либо экзогенного влияния соотношение популяций изменится, то общая популяция птиц со временем вновь придет к старому равновесному состоянию.
• Числа в этой таблице обозначают выживаемость соответствующих видов птиц при встрече друг с другом. Если в начале игры обе популяции имеют одинаковое количество особей, то вероятность того, что голубь встретит другого голубя или сокола составляет в обоих случаях 0, 5. Среднее значение выживаемости голубя составит 0, 5· 1 + 0, 5· 0 = 0, 5, а для сокола 0, 5· 2 + 0, 5·(– 1) = 0, 5. • Так как в этом случае оба вида птиц имеют одинаковое значение выживаемости, то соотношение их численности со временем не изменится. Если этой игре с помощью дифференциальных уравнений придать динамику, то окажется, что популяции обоих видов птиц одинаковой величины стабильны по численности; если же в результате какого-либо экзогенного влияния соотношение популяций изменится, то общая популяция птиц со временем вновь придет к старому равновесному состоянию.
 • Особое место в теории игр занимают способы выявления того, какова истинная оценка полезности блага (инвестиционного проекта) у его покупателя. Среди них наибольшую популярность у экономистов получили "аукцион второй цены" и "налог Кларка". Изобретение аукциона второй цены считается одним из важнейших достижений американского экономиста Вернона Смита, получившего за свои результаты работы в области теории игр Нобелевскую премию за 2002 год.
• Особое место в теории игр занимают способы выявления того, какова истинная оценка полезности блага (инвестиционного проекта) у его покупателя. Среди них наибольшую популярность у экономистов получили "аукцион второй цены" и "налог Кларка". Изобретение аукциона второй цены считается одним из важнейших достижений американского экономиста Вернона Смита, получившего за свои результаты работы в области теории игр Нобелевскую премию за 2002 год.


