Теория игр для международников и политологов Д А

Теория игр для международников и политологов Д. А. Дегтерев Москва-2008

Лекция 1 Классификация игр и формы их представления Содержание лекции 1 1. История развития теории игр 2. Связь теории игр с другими дисциплинами 3. Применение теории игр к анализу международных отношений и в политологии 4. Ограничения применения теории игр 5. Структура курса 6. Литература по теории игр Москва-2008

Классификация игр и формы их представления Лекция 1 История развития теории игр • Предварительный этап ( «до монографии» ) • 1944 - Теория игр и экономическое поведение (Джон фон Нейман и Оскар Моргенштерн) • 1950 г. – Бескоалиционные игры (Джон Нэш) • 1950 – 1970 гг. – Доминирование «коалиционного подхода» Дж. фон Неймана и О. Моргенштерна • Москва-2008 1970 – н. в. – развитие «программы Нэша»

Классификация игр и формы их представления Лекция 1 История развития теории игр Предварительный этап ( «до монографии» ) • «Исследование математических принципов теории богатства» (А. Курно, 1838) • Работы Бертрана, Лаунхарда, Эджуорта (экономисты XIXвека) • «О применении теории множеств к теории шахматной игры» (Е. Цермело, 1913) • «Теория игр и интегральные уравнения с кососимметричными ядрами» (Э. Борель, 1921) • «Определения теории игр и преследования» (Штейнгауз, 1925) • «Über eine Schlussweisse aus dem Endlichen ins Unedliche» (Д. Кениг, 1927) • «К теории стратегических игр» (Дж. фон Нейман, Москва-2008 1928)

Классификация игр и формы их представления Лекция 1 История развития теории игр • 1944 г. – Теория игр и экономическое поведение (Джон фон Нейман и Оскар Моргенштерн) – – – • Новый инструментарий для математического анализа экономических процессов Игры с нулевой суммой Коалиционные игры 1950 г. – Бескоалиционные игры (Джон Нэш) – – – Равновесие по Нэшу Бескоалиционные игры Москва-2008 «Программа Нэша»

Классификация игр и формы их представления Лекция 1 • История развития теории игр 1950 – 1970 гг. – Доминирование «коалиционного подхода» Дж. фон Неймана и О. Моргенштерна – – – • Теория игр как стратегическое оружие «холодной» войны. Разработки РЭНДКорпорэйшн. «Золотой век» теории игр Разочарования (сложность практического применения; цинизм) 1970 – н. в. – развитие «программы Нэша» – – Равновесие по Нэшу – базовая концепция теории игр Повсеместное использование в экономике. Работы Р. Зельтена и Дж. Харшаньи – Нобелевская премия по экономике 1994 г. Москва-2008 (+Дж. Нэш)

Классификация игр и формы их представления Лекция 1 Связь теории игр с другими дисциплинами Теория игр – математическая теория анализа стратегического поведения/ взаимодействия сторон/ конфликтов: 1. Математическая теория – использует инструментарий математических наук 2. Сфера применения – чрезвычайно широка, в т. ч. взаимодействие индивидуумов (групп индивидуумов) – область общественных (социальных) наук Теория игр объясняет логику рационального поведения индивидуумов в условиях конфликта Москва-2008 интересов

Классификация игр и формы их представления Лекция 1 Связь теории игр с другими дисциплинами Смежные математические науки 1. Теория принятия решений – в рамках анализа экстенсивной формы игры 2. Теория вероятностей / математическая статистика в рамках анализа «игр с природой» 3. Линейная (векторная) алгебра – в рамках использования матричного подхода для нормальной формы игры и вектора выигрышей игр с большим числом игроков 4. Теория множеств – в рамках доказательства теорем теории игр (в т. ч. центральной – о минимаксе) 5. Исследование операций – теория игр как частный случай оптимизации работы системы из n-игроков, что изучается в рамках исследования операций Москва-2008

Классификация игр и формы их представления Лекция 1 Связь теории игр с другими дисциплинами Смежные общественные науки 1. Теория рационального выбора – в рамках определения рациональности поведения участников игры 2. Теория социального и общественного выбора – в рамках анализа механизма формирования и распада коалиций 3. Теория прав собственности (теория контрактов) – в рамках определения правил игры 4. Экспериментальная экономика – в рамках проверки положений теории игр Москва-2008

Классификация игр и формы их представления игр к анализу Применение теории Лекция 1 международных отношений и в политологии Международные отношения • Контроль над вооружениями. Разоруженческая проблематика • Анализ военно-политических конфликтов • Политика устрашения (угрозы) • Соблюдение международных соглашений • Ведение международных переговоров Работы: • «Стратегия конфликта» (Томас Шеллинг, 1960 г. ) Москва-2008

Классификация игр и формы их представления игр к анализу Применение теории Лекция 1 международных отношений и в политологии Политология • Прогноз итогов голосования • Оптимизация предвыборной платформы при известном политическом спектре избирателей • Парламентские (политические) коалиции • Анализ процесса принятия решений в коллегиальных органах (с учетом квот) Работы: • «Теория игр и политическая теория» (Петер Ортешук, 1986 г. ) Москва-2008

Классификация игр и формы их представления Лекция 1 Ограничения применения теории игр Теория игр – инструмент анализа (и лишь в редких случаях – решения) конфликтных ситуаций между двумя и более сторонами • В теории игр ситуация оптимизируется лишь по одному критерию (выигрышу), в реальности – решение ищется во многокритериальном пространстве • Неполная информация о реальном количестве игроков, об участии игроков сразу в нескольких играх, о выигрыше противника • Сложность количественной оценки выигрышей при построении матрицы игры • В реальности рациональность выбора людей носит ограниченный характер, зависит от убеждений, Москва-2008 моральных норм, обстоятельств

Классификация игр и формы их представления Лекция 1 Ограничения применения теории игр • На принятие решения влияют не только сами лидеры, но и группы экспертов, окружение (фактически решения принимаются не теми лицами, кто формально отвечает за это) • Роль «человеческого» фактора при реализации решений, принятых на высоком уровне • Техническая сложность решения игр в чистых стратегиях при большом числе стратегий (например, шахматы) • Техническая сложность решения игр в смешанных стратегиях при числе стратегий свыше 10 (невозможность обработки данных в стандартных математических программах) Москва-2008 • Игры с числом игроков 5 и более имеют строгое математическое решение лишь в частных случаях

Классификация игр и формы их представления Лекция 1 Структура курса • РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИГР • РАЗДЕЛ 2. ТЕОРЕТИКО-ИГРОВОЙ АНАЛИЗ МО • РАЗДЕЛ 3. ТЕОРИЯ ИГР И ПОЛИТОЛОГИЯ • РАЗДЕЛ 4. ПРИМЕНЕНИЕ ТЕОРИИ ИГР В ЭКОНОМИКЕ Москва-2008

Классификация игр и формы их представления Лекция 1 Структура курса • РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИГР – – – Лекция 1. Классификация игр и формы их представления Лекция 2. Решение бескоалиционных игр в чистых стратегиях Лекция 3. Игры в смешанных стратегиях Москва-2008

Классификация игр и формы их представления Лекция 1 Структура курса • РАЗДЕЛ 2. ТЕОРЕТИКО-ИГРОВОЙ АНАЛИЗ МЕЖДУНАРОДНЫХ ОТНОШЕНИЙ – – – Лекция 4. Простые игровые модели международных конфликтов Лекция 5. Игры с неполной информацией и дезинформацией Лекция 6. Динамические модели переговоров Москва-2008

Классификация игр и формы их представления Лекция 1 Структура курса • РАЗДЕЛ 3. ТЕОРИЯ ИГР И ПОЛИТОЛОГИЯ – Лекция 7. Применение теории игр к анализу выборов и голосования в коллективных органах • РАЗДЕЛ 4. ПРИМЕНЕНИЕ ТЕОРИИ ИГР В ЭКОНОМИКЕ – Лекция 8. Модели конкуренции и оптимизация сотрудничества Москва-2008

Классификация игр и формы их представления Лекция 1 Структура курса ФОРМЫ ПРОВЕДЕНИЯ ЗАНЯТИЙ: • Изложение теоретических основ (не менее 20 -30 мин) • Решение количественных примеров и задач • Проведение аудиторных экспериментов • Индивидуальные доклады по биографии и обзору работ основоположников теории игр • Теоретико-игровой анализ реальных международных и внутриполитических ситуаций (кейсов) • Самостоятельный теоретико-игровой анализ международной или внутриполитической ситуации (на выбор) Москва-2008

Классификация игр и формы их представления Лекция 1 Литература • Нетехническое введение в теорию игр – Низкий уровень сложности – Высокий уровень сложности • Применение теории игр в политологии и международных отношениях – Низкий уровень сложности – Высокий уровень сложности Москва-2008

Классификация игр и формы их представления Лекция 1 Литература Нетехническое введение в теорию игр: • Низкий уровень сложности • Вильямс Дж. Д. Совершенный стратег или букварь по теории стратегических игр. – М. : Советское радио, 1960. – 269 с. • Данилов В. Лекции по теории игр. - М. : РЭШ, 2002. – 140 с. • Печерский С. Л. , Беляева А. А. Теория игр для экономистов. - СПб. , 2001. – 253 с. • Высокий уровень сложности • Льюис Р. Д. , Райфа Х. Игры и решения. – М. : ИЛ, 1961. – 642 с. • Мулен Э. Теория игр с примерами из математической экономики. – М. : Мир, 1985. – 200 с. • Davis Morton D. Game Theory: a Nontechnical Москва-2008 Introduction. – Dover Publications, 1997.

Классификация игр и формы их представления Лекция 1 Литература Применение теории игр в политологии и в МО: • Низкий уровень сложности • Brams Steven J. Game Theory and Politics. Dover Pub. , 2004. • Diplomacy Games. Formal Models and International Negotiations. Springer 2007. • Gates S. , Humes B. Games, Information and Politics. Applying Game Theoretic Models to Political Science. UMP, 2007. • Высокий уровень сложности • Шеллинг Т. Стратегия конфликта. – М. : ИРИСЭН, 2007. – 366 с. • Mayerson R. B. Game Theory. Analysis of Conflict. Harvard University Press, 1997. Москва-2008 • Ordeshook Peter C. Game Theory and Political Theory.

Лекция 2 Решение бескоалиционных игр в чистых стратегиях Содержание лекции 2 1. 2. 3. 4. Типы игр и их взаимосвязь Нормальная форма представления игры Описание игры в виде графа Исключение заведомо слабых стратегий (итерационное доминирование). 5. Выбор оптимального ответного хода (BR). 6. Принцип минимакса. 7. Седловые точки и равновесие по Нэшу Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Типы игр и их взаимосвязь В зависимости от выигрыша (проигрыша): • Игры с нулевой (постоянной) суммой - выигрыш одной стороны равен проигрышу другой – Парные игры с нулевой суммой – антагонистические – Безобидные (честные) игры – средний выигрыш каждого игрока при разумном поведении = 0 • Игры с ненулевой (переменной) суммой – сумма выигрышей всех игроков не равна константе, а меняется в зависимости от выбора стратегий Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Типы игр и их взаимосвязь В зависимости от выигрыша (проигрыша): • Игры с нулевой (постоянной) суммой – встречаются крайне редко – «Чистые конфликты» – Локальные столкновения в ходе вооруженных конфликтов – Спортивные соревнования • Игры с ненулевой (переменной) суммой – основная часть жизненных ситуаций – Игроки имеют как противоположные, так и общие интересы – Война (не использовать запрещенные виды оружия, обмен военнопленными) Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Типы игр и их взаимосвязь В зависимости от характера взаимодействия между игроками: • Кооперативные (коалиционные) игры – игроки могут объединяться в группы, беря на себя некоторые обязательства перед другими игроками и координируя свои действия, в т. ч. на основе предварительных договоренностей (и торга) • Некооперативные (бескоалиционные) игры – каждый играет за себя – на практике распространены гораздо шире Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Типы игр и их взаимосвязь В зависимости от цели: • Игры качества - для каждой из сторон исход игры фактически двузначен – да или нет (победилпроиграл) • Игры степени - желательность исхода игры определяется значением численного параметра (плата, выигрыш) Дискретные игры - выбор производится не из непрерывного множества допустимых значений, а из заданного набора отдельных альтернатив Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Типы игр и их взаимосвязь В зависимости от числа ходов: • Одномоментные игры – в основном рассматриваются в теории игр • Многоходовые игры – при их анализе используется дерево игры Конечные игры – игры с конечным числом ходов и конечным числом чистых стратегий на каждом ходе Бесконечные игры – игры, в которых игроки имеют бесконечное число чистых стратегий для выбора Любую последовательность ходов можно представить как одномоментный выбор стратегии Москва-2008 поведения

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Нормальная форма представления игры Платежная матрица (матрица выигрышей) представление игры в нормальной форме - Каждый элемент матрицы представляет собой выигрыш первого игрока и проигрыш второго игрока при определенной ситуации (в играх с нулевой суммой) Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Нормальная форма представления игры Пример 1: • Играют 2 человека, показывают от 1 до 3 пальцев • Если общее число пальцев четное – выиграл 1 -й игрок, его выигрыш (проигрыш 2 -го игрока) равен числу пальцев • Если сумма пальцев нечетная - выиграл 2 -й игрок, его выигрыш (проигрыш 1 -го игрока) равен числу пальцев • В матрицу 3 х 3 записывается сумма выигрыша (проигрыша) Москва-2008 • Это игра с нулевой суммой, у каждого игрока по 3

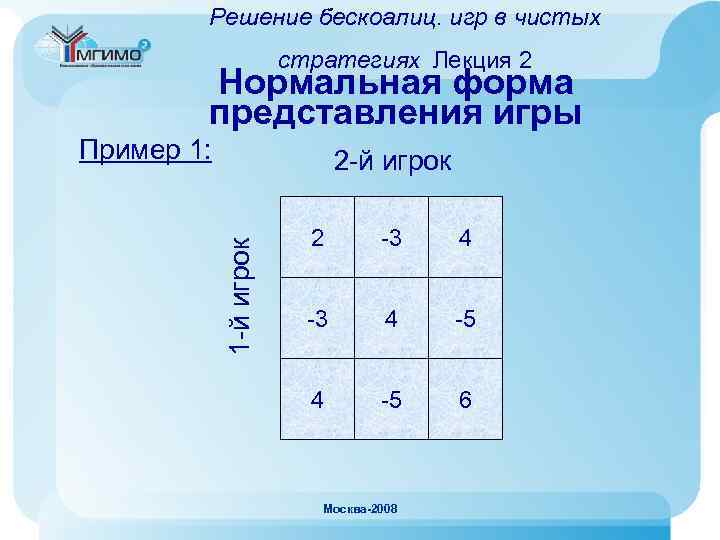Решение бескоалиц. игр в чистых стратегиях Лекция 2 Нормальная форма представления игры Пример 1: 1 -й игрок 2 -3 4 -5 6 Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Нормальная форма представления игры Пример 2: • Играют 2 человека, бросают игральную кость (кубик) • Если общее число очков четное – выиграл 1 -й игрок, его выигрыш (проигрыш 2 -го игрока) равен сумме очков • Если сумма очков нечетная - выиграл 2 -й игрок, его выигрыш (проигрыш 1 -го игрока) равен сумме очков • В матрицу 6 х 6 записывается сумма выигрыша (проигрыша) • Это игра с нулевой суммой, у каждого игрока по 6 Москва-2008 стратегий

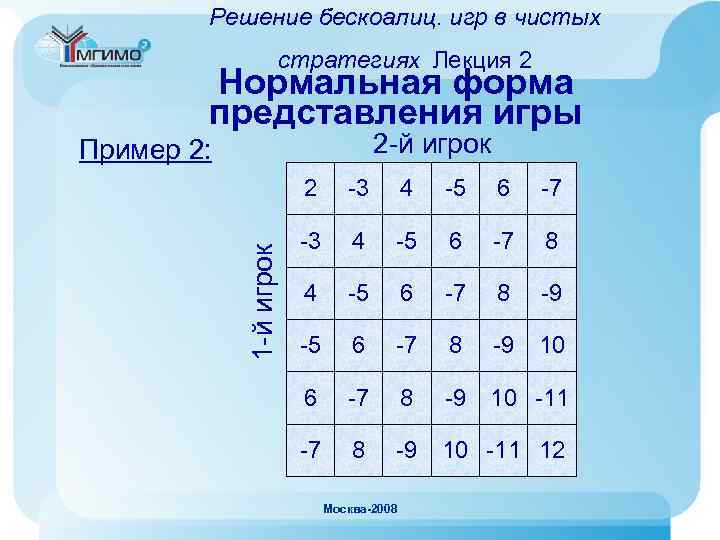Решение бескоалиц. игр в чистых стратегиях Лекция 2 Нормальная форма представления игры 2 -й игрок Пример 2: 1 -й игрок 2 -3 4 -5 6 -7 8 -9 10 6 -7 8 -9 10 -11 12 Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Описание игры в виде графа Стратегия – вся последовательность ходов игры Вильямс: Это план, настолько исчерпывающий, что он не может быть нарушен действиями противника или природы Позиционное (развернутое) представление игры альтернатива нормальной формы Дерево игры - развернутая (экстенсивная) форма представления многоходовой игры, где каждая вершина соответствует ситуации выбора игроком своей стратегии Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Описание игры в виде графа Информационное множество (information set) – при выборе игроком своего хода он может не знать, в какой позиции игры он находится, потому что не знает, какой ход был сделан противником на предыдущем этапе (ах). Информационное множество – совокупность таких «неразличимых» позиций. Ходы, возможные в этих позициях, одинаковы. Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Итерационное доминирование Исключение заведомо слабых стратегий игроков - просматриваются все строки (для 1 -го игрока) матрицы и вычеркиваются те, в которых все соответствующие элементы меньше, чем в хотя бы одной другой строке Аналогично рассуждает и второй игрок, с той разницей, что он выбирает столбцы, а не строки и стремится уменьшить, а не увеличить выигрыш первого игрока. Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Итерационное доминирование После того как вычеркнуты некоторые столбцы, надо опять повторить эту процедуру, так как строки стали другими и могло изменится соотношение между ними. При просмотре опять могут быть выявлены «заведомо слабые» стратегии первого игрока. Соответственно и анализ столбцов потом придется повторить. Повторение однотипных шагов, которые в математике называют итерациями, - итерационное доминирование Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 1 -й игрок Итерационное доминирование 2 -й игрок 1 3 Пример 3: 2 1<3 и 2<4 4 Первый игрок в любом случае получит больше, если выберет вторую стратегию, независимо от выбора второго игрока. Первая строка строго доминируется второй Москва-2008

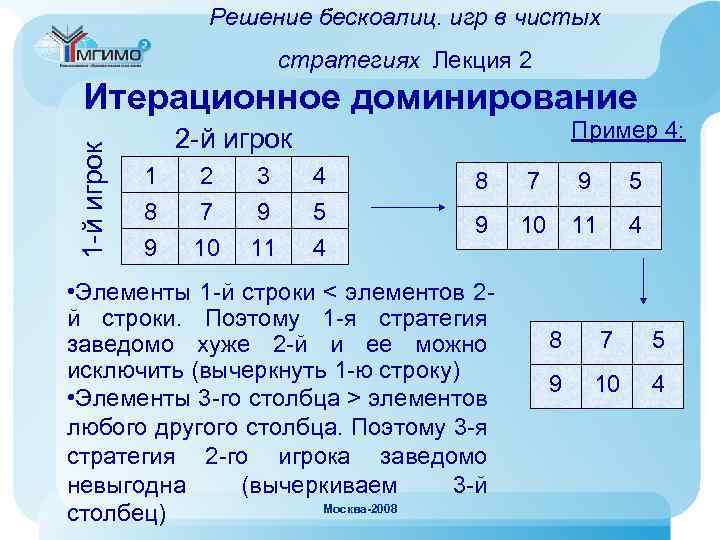Решение бескоалиц. игр в чистых стратегиях Лекция 2 1 -й игрок Итерационное доминирование Пример 4: 2 -й игрок 1 8 9 2 7 10 3 9 11 4 5 4 8 7 9 5 9 10 11 4 • Элементы 1 -й строки < элементов 2 й строки. Поэтому 1 -я стратегия заведомо хуже 2 -й и ее можно исключить (вычеркнуть 1 -ю строку) • Элементы 3 -го столбца > элементов любого другого столбца. Поэтому 3 -я стратегия 2 -го игрока заведомо невыгодна (вычеркиваем 3 -й Москва-2008 столбец) 8 7 5 9 10 4

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Выбор оптимального ответного хода (BR) • Один из игроков уже сделал выбор, его знает противник и исходя из этой информации делает свой выбор. Задача выбора оптимального ответного хода - BR (best response) • Если известен выбор 2 -го игрока, то 1 -му достаточно просмотреть только один столбец матрицы, соответствующий номеру выбранной стратегии 2 -го игрока, и выбрать ту строку, где стоит максимальный в данном столбце элемент Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Выбор оптимального ответного хода (BR) 2 -й игрок Пример 5: 1 -й игрок 0 2 0 1 2 3 4 5 6 7 8 9 0 9 5 3 4 1 7 6 5 4 3 Если известно, что 2 -й игрок выбрал 1 -ю стратегию, то достаточно просмотреть лишь 1 -й столбец матрицы и найти в нем максимальный элемент. Это число 9, стоящее в 4 -й строке. Значит оптимальным ответным ходом (BR) 1 -го игрока является 4 -я Москва-2008 стратегия.

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Принцип минимакса • Каждый игрок в гарантированного выбор) теории игр – сторонник выигрыша (рациональный • Просмотрев min для всех строк матрицы, 1 -й игрок выбирает ту строку, где это число max. Это гарантированный выигрыш, не зависящий от выбора 2 -го игрока. Если повезет – можно выиграть и больше, но меньше нельзя в принципе Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Принцип минимакса • Поскольку эта процедура связана сначала с нахождением min строк, а потом max среди них, то рассмотренный принцип решения игр называется принципом максимина или минимакса (ведь 2 -й игрок сначала находит максимумы во всех столбцах матрицы и потом из них выбирает минимальный). • Выбранные таким образом стратегии игроков называются соответственно максиминными и минимаксными. Из-за благозвучности чаще используется термин «принцип минимакса» , а не максимина Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 1 -й игрок Принцип минимакса 2 -й игрок 1 2 3 4 Пример 6: • В 1 -й строке минимум равен 1, во 2 -й – 2. Поэтому рациональный выбор 1 -го игрока соответствует 2 -й стратегии • В 1 -м столбце максимум равен 3, во 2 -м - 4. Поэтому минимаксная стратегия 2 -го игрока – это 1 -я стратегия. • Таким образом, первый игрок выберет вторую стратегию, второй – первую. • HO! Если 2 -й игрок узнает, что 1 -й выбрал свою 2 -ю стратегию, ему Москва-2008 выгоднее ответить своей 2 -й

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Принцип минимакса Пример 6: • В данном случае минимаксные стратегии неустойчивы и игра не решается в чистых стратегиях. • Нельзя сказать, чему равен выигрыш 1 -го игрока (он называется ценой игры), но можно вычислить границы интервала, в котором он находится. • Нижней ценой игры называется максимальное значение минимумов строк (в примере она равна 2), • Верхней ценой игры называют минимальное значение максимумов столбцов (в примере это 3). • Если верхняя и нижняя цена игры совпадают, то игра решается в чистых стратегиях. В противном случае ищется решение в смешанных стратегиях, причем цена игры всегда оказывается между ее Москва-2008 нижней и верхней ценами.

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Седловые точки и равновесие по Нэшу • Элемент матрицы игры, стоящий на пересечении минимаксных строки и столбца, принято называть при устойчивых минимаксных стратегиях седловой точкой. • Это название связано с тем, что данный элемент одновременно является минимальным в своей строке и максимальным – в столбце. • Из условия минимума по строке и максимума в столбце следует единственность числа в седловой точке. То есть самих таких точек может быть несколько, но выигрыш в них один и тот же. Поэтому для игроков они равноценны. Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Седловые точки и равновесие по Нэшу • Именно с проверки на наличие седловой точки рекомендуется начинать анализ игры, представленной в нормальной форме. При ее наличии сразу получается решение игры – устойчивые минимаксные стратегии обоих игроков и значение цены игры. • Если такой точки нет, то делается вывод, что игра не решается в чистых стратегиях. Тогда применяется итерационное доминирование и методы решения игры в смешанных стратегиях. Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Седловые точки и равновесие по Нэшу • Именно с проверки на наличие седловой точки рекомендуется начинать анализ игры, представленной в нормальной форме. При ее наличии сразу получается решение игры – устойчивые минимаксные стратегии обоих игроков и значение цены игры. • Если такой точки нет, то делается вывод, что игра не решается в чистых стратегиях. Тогда применяется итерационное доминирование и методы решения игры в смешанных стратегиях. Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Седловые точки и равновесие по Нэшу • В биматричных играх (играх с ненулевой суммой) нет минимаксных стратегий и самого понятия цены игры, потому что выигрыш 2 -го игрока может быть и не связан с выигрышем 1 -го игрока. • НО существует нечто похожее на понятие седловой точки: если в некотором столбце матрицы 1 -го игрока имеется максимум в некоторой точке и в матрице 2 -го игрока строка, проходящая через аналогичную точку, тоже имеет максимум именно в этой точке, то обоим игрокам выгодно придерживаться стратегий, соответствующих номерам строки и столбца этой точки. Данную пару или набор стратегий принято называть устойчивыми по Нэшу Москва-2008

Решение бескоалиц. игр в чистых стратегиях Лекция 2 Седловые точки и равновесие по Нэшу • Устойчивость по Нэшу определена и при числе игроков более 2. Это такой набор стратегий, при котором ни одному из игроков не выгодно менять стратегию при условии, что остальные игроки будут придерживаться своей прежней стратегии. Москва-2008

Лекция 3 Игры в смешанных стратегиях Содержание лекции 3 1. Частота применения разных стратегий 2. Матричный метод определения оптимальных смешанных стратегий и цены игры для игр 2 х2. 3. Графический метод решения игр 2 хm и 3 хm. Москва-2008

Игры в смешанных стратегиях Лекция 3 Частота применения разных стратегий • Большинство игр с нулевой суммой не поддается решению в чистых стратегиях. • Иногда возможно уменьшить матрицу игры путем исключения доминируемых и дублирующих стратегий (если удалось ее свести к одной строке или одному столбцу - игра решена в чистых стратегиях даже без использования принципа минимакса и нахождения седловой точки) • Приходится признать, что ни одна из чистых стратегий не является оптимальной. В ТАКИХ СЛУЧАЯХ: • Необходимо чередовать стратегии в определенной пропорции. Решением игры в этом случае является как раз такая пропорция. Москва-2008

Игры в смешанных стратегиях Лекция 3 Частота применения разных стратегий • Если у игрока 3 чистых стратегии и мы после определенных расчетов говорим – ему надо использовать эти стратегии в пропорции 5: 1: 4. • Могут стоять любые натуральные числа или даже ноль. • В последнем случае говорят, что соответствующая стратегия не используется в смеси стратегий и является неактивной. • Те же, которые используются, называют активными стратегиями. • Поведение игрока, связанное с чередованием его стратегий, называют смешанной стратегией. Москва-2008

Игры в смешанных стратегиях Лекция 3 Частота применения разных стратегий • Основная теорема теории игр (теорема Неймана, теорема о минимаксе): Любая парная игра с нулевой суммой имеет решение в чистых или смешанных стратегиях. • Это решение определяет оптимальные минимаксные стратегии игроков и цену игры. • Использование любой другой стратегии в среднем менее выгодно каждому из игроков. • Цена игры всегда находится между нижней и верхней ценой матрицы игры. • Решение в чистых стратегиях – это частный случай решения в смешанных стратегиях (когда в смеси активна лишь одна стратегия). Москва-2008

Игры в смешанных стратегиях Лекция 3 Частота применения разных стратегий • Если смешанная стратегия выражена в виде пропорции, то стоящие в ней числа называют относительными частотами применения стратегий. • Другой способ задания смешанной стратегии - через вероятности реализации чистых стратегий. Их легко рассчитать по известным относительным частотам. Пусть например задана смесь 4 -х стратегий в виде пропорции N 1: N 2: N 3: N 4. Тогда вероятность реализации первой стратегии равна: р1 = N 1/( N 1+ N 2+ N 3+ N 4) • Аналогично рассчитываются и остальные 3 вероятности р2, р3, р4. • Естественно, что сумма всех вероятностей в этом Москва-2008 случае равна 1.

Игры в смешанных стратегиях Лекция 3 Частота применения разных стратегий • Если действия по реализации стратегий производятся многократно, то вполне достаточно буквального использования относительных частот. В этом случае существует риск того, что противник просчитает следующий ход. • Поэтому в теории игр обычно используется другой способ, который в принципе исключает возможность знать следующий ход. Он основан на вероятностном подходе и связан с использованием датчика случайных чисел: компьютерной программы, бросания монетки или игральной кости. • Любые вычислительные методы, использующие датчик случайных чисел, принято называть методами Монте-Карло. По методу Монте-Карло Москва-2008 можно реализовать смешанную стратегию даже в

Игры в смешанных стратегиях Лекция 3 Матричный метод определения смешанных стратегий и цены игры Пример 1. Игра «наступление-оборона» • Обороняющая сторона защищает 2 объекта, причем один из них в 3 раза важнее другого. Сил достаточно только на охрану одного из объектов, причем при нападении на охраняемый объект побеждает оборона. У нападения тоже сил достаточно только для атаки одного объекта. • Какой из объектов надо охранять и на какой надо нападать? _______________________ • Типичная парная игра 2 х2. • Первая стратегия обороны – защитить важный Москва-2008 объект, вторая – защитить не важный.

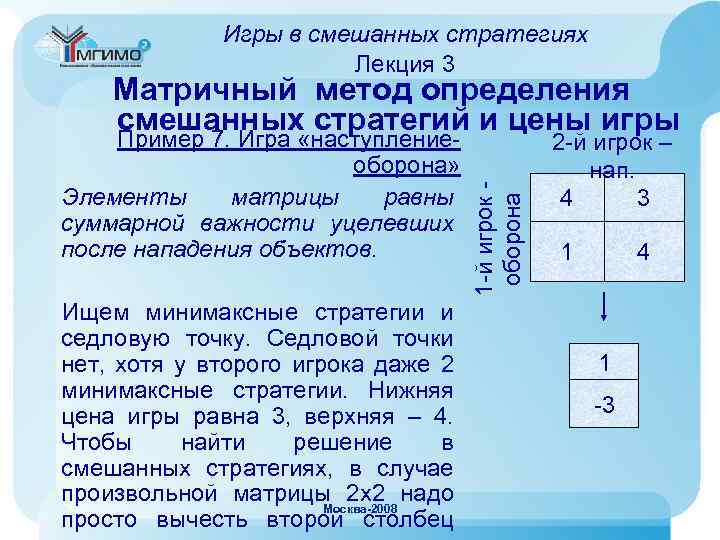Игры в смешанных стратегиях Лекция 3 Пример 7. Игра «наступлениеоборона» Элементы матрицы равны суммарной важности уцелевших после нападения объектов. Ищем минимаксные стратегии и седловую точку. Седловой точки нет, хотя у второго игрока даже 2 минимаксные стратегии. Нижняя цена игры равна 3, верхняя – 4. Чтобы найти решение в смешанных стратегиях, в случае произвольной матрицы 2 х2 надо Москва-2008 просто вычесть второй столбец 1 -й игрок оборона Матричный метод определения смешанных стратегий и цены игры 2 -й игрок – нап. 4 3 1 4 1 -3

Игры в смешанных стратегиях Лекция 3 Матричный метод определения смешанных стратегий и цены игры 1 Пример 7. Игра «наступление-оборона» Отношение двух полученных разностей (независимо от их знаков) равно оптимальному соотношению применения 1 -м игроком 2 -й и 1 -й стратегий. -3 Обратим внимание – отношение первой разности ко второй равно отношению частот именно 2 -й и 1 -й стратегий в оптимальной смеси. Москва-2008

Игры в смешанных стратегиях Лекция 3 Матричный метод определения смешанных стратегий и цены игры Пример 7. Игра «наступление-оборона» • Аналогично вычитают 2 -ю строку исходной матрицы из первой, отношение полученных разностей задает оптимальное отношение частоты применения вторым игроком его второй и первой стратегий. Разность строк дает: (3 -1), значит у нападения относительные частоты применения чистых стратегий 1: 3. 3 -1 Обороне надо использовать стратегии с частотами 3: 1, то есть в 3 раза чаще охранять важный объект. Нападать надо чаще на менее важный объект Москва-2008

Игры в смешанных стратегиях Лекция 3 Матричный метод определения смешанных стратегий и цены игры Пример 7. Игра «наступление-оборона» • Аналогично вычитают 2 -ю строку исходной матрицы из первой, отношение полученных разностей задает оптимальное отношение частоты применения вторым игроком его второй и первой стратегий. Разность строк дает: (3 -1), значит у нападения относительные частоты применения чистых стратегий 1: 3. 3 -1 Обороне надо использовать стратегии с частотами 3: 1, то есть в 3 раза чаще охранять важный объект. Нападать надо чаще на менее важный объект Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр • Графический метод - построение графиков зависимости выигрыша от пропорции, в которой смешаны 2 стратегии 1 -го игрока • Применим не только к играм 2 х2, но и к играм, в которых у 2 -го игрока число стратегий m > 2 (игры 2 хm). Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр • Рассмотрим матрицу игры аij размерности 2 хm. • Пусть у 1 -го игрока доля (вероятность) первой стратегии в смеси равна х, тогда доля второй (1 -х). • Если 2 -й игрок использует чистую первую стратегию, то выигрыш первого составит: х*а 11 + (1 -х)*а 21 = а 21 + (а 11 - а 21)х Москва-2008

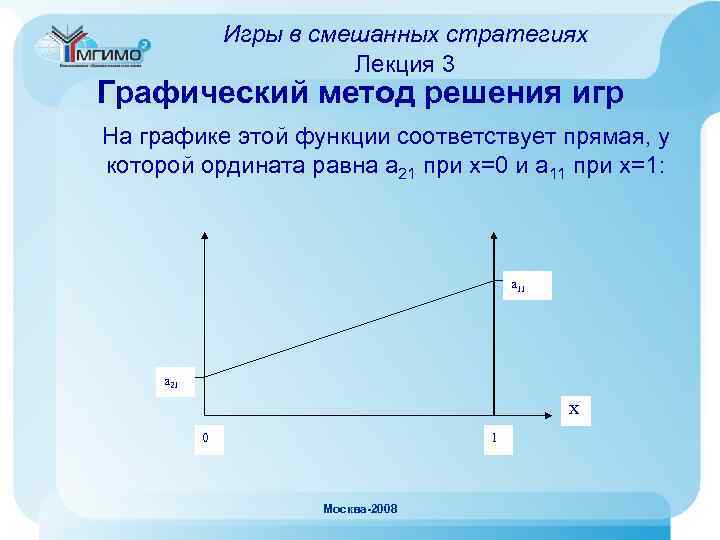Игры в смешанных стратегиях Лекция 3 Графический метод решения игр На графике этой функции соответствует прямая, у которой ордината равна а 21 при х=0 и а 11 при х=1: a 11 a 21 X 0 1 Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр • Если у второго игрока 3 стратегии (m = 3), то на таком графике будет 3 линии. • Каждая из них строится аналогично – на левой оси откладывается значение a 2 j , а на правой a 1 j. Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр 4 7 1 2 1 5 Пример 8 Задана матрица игры, необходимо решить игру графическим методом. • Слева на графике откладывают числа со второй строки матрицы (2, 1, 5), справа – с первой (4, 7, 1). Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр Пример 8 • Противник выберет такие стратегии, чтобы ваш выигрыш был меньше. На графике этому соответствует нижняя ломаная линия из трех отрезков. • А вы выберете на ней максимум (откуда опущен пунктир на ось). Абсцисса этой точки соответствует оптимальной доли первой стратегии х для первого игрока, а ее ордината равна цене игры. 7 5 X 0 1 Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр • Оптимальная смесь стратегий 2 -го игрока определяется потом путем дополнительных расчетов, хотя сразу можно сказать, что противнику следует использовать только те стратегии, линии которых проходят через выделенную точку (первая и третья в данном случае). • Поэтому можно просто вычеркнуть второй столбец из матрицы и для оставшейся матрицы 2 х2 найти решение. Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр Игры 3 хm (у 1 -го игрока 3 стратегии) решаются аналогично в трехмерном пространстве. При этом каждой чистой стратегии 2 -го игрока теперь соответствует не прямая, а плоскость. Эти плоскости образуют конструкцию типа крыши и надо сначала выделить самую нижнюю «крышу» , а потом найти координаты ее верхней точки. Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр Функция «Поиск решения» (EXCEL) Программа EXCEL, меню «Сервис» , функция «Поиск решения» Пример 9 Пусть у первого игрока n стратегий, а у второго m. Надо найти оптимальные доли стратегий рi в их смеси для первого игрока. • Обозначим цену игры ν, тогда при использовании противником любой из его m стратегий выигрыш первого игрока будет не меньше ν. Выразив этот выигрыш через рi и элементы матрицы игры, получим соответствующие m неравенств вида: a 1 j p 1 + a 2 j p 2 + … + anj pn ≥ ν Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр Функция «Поиск решения» (EXCEL) Пример 9 Если обе части разделить на ν и обозначить хj = pj/ν, то неравенства преобразуются к виду: a 1 j х1 + a 2 j х2 + … + anj хn ≥ 1 ( 1 ) Кроме того должно выполняться условие на сумму всех долей: p 1 + p 2 + … + pn = 1, которое для переменных х имеет вид: х1 + х2 + … + хn = 1/ν. ( 2 ) Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр Функция «Поиск решения» (EXCEL) Пример 9 • Так как 1 -й игрок стремится повысить цену игры, последнюю сумму можно рассматривать как функцию цели и решать задачу по нахождению оптимальных значений переменных хj, на которые наложено ограничение (1). • С этой целью на рабочем листе EXCEL для каждой переменной хj заводим по ячейке и записываем туда некоторые начальные значения, соответствующие ограничениям (1). Например, это могут быть просто нули и единицы. • После этого в одной из ячеек задаем х1 + х2 + … + хn и указываем имя этой ячейки в меню «Поиск решения» на месте функции цели. Указываем также поиск минимума функции. Москва-2008

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр Функция «Поиск решения» (EXCEL) Пример 9 • Задаем платежную матрицу на рабочем листе и через имена соотв. ячеек выражаем ограничения на значения х. • Для этого заводим ячейки на рабочем листе для вычисления левых частей неравенств (1), после чего в «Поиске решения» указываем в левой части имена этих ячеек, потом знак ≥, потом в правой части 1. • Указывается также ограничение на знак величин хj ≥ 0, при этом опять в левой части указывается только имя ячейки, соответствующей хj. • Далее дается команда «Найти» и в ячейках для хj Москва-2008 появляются оптимальные значения.

Игры в смешанных стратегиях Лекция 3 Графический метод решения игр Функция «Поиск решения» (EXCEL) Пример 9 • Сумма оптимальных значений позволяет найти цену игры, пользуясь (2), после чего находятся и сами оптимальные доли стратегий в смеси рj = хj * ν. • Аналогично находится оптимальная смесь стратегий 2 -го игрока, только теперь потребуется максимизировать функцию цели. Москва-2008

Лекция 4 Простые игровые модели международных конфликтов Содержание лекции 4 1. Теоретико-игровой анализ Карибского кризиса. 2. Применение вероятной (дозированной) угрозы (brinkmanship). Москва-2008

Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса Ситуация • В сентябре-октябре 1962 г. СССР развертывал на Кубе ракетную базу. Установил 40 ракет с ядерными боеголовками. Ракеты доставлялись на Кубу морем в обстановке полной секретности. • База должна была быть полностью оборудована к середине ноября, но 14 октября самолет-разведчик США сфотографировал уже развернутые ракеты и 16 октября после расшифровки снимков информацию о развернутых ракетах и средствах их защиты сообщили президенту США Дж. Кеннеди. • Дж. Кеннеди провел совещание в узком кругу экспертов и в течение недели принял решение объявить морскую блокаду Кубы. США требовали убрать ракеты, угрожая драматическими Москва-2008 последствиями. Советский лидер Никита Хрущев

Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса Ситуация • 2 недели мир стоял на грани ядерной войны. 26 октября Кеннеди объявил ультиматум, требуя в 24 часа принять решение о демонтаже ракет в обмен на обещание США отказаться от нападения на Кубу. • Руководство США объявило мобилизацию резервистов и стало готовиться к нанесению удара по базе (а возможно и по СССР). Было принято решение о начале военных действий при игнорировании ультиматума не позднее 29 октября. • Но 27 октября Хрущев согласился убрать ракеты с Кубы и конфликт был исчерпан. К 20 ноября ракеты были вывезены с Кубы. Москва-2008

Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса Представим событие в виде парной игры с ненулевой суммой: • 1 -й игрок (США) после развертывания советских ракет выбирает одну из двух возможных стратегий – либо угрожать СССР военными действиями вплоть до ядерной войны, либо смириться с новой угрозой. В последнем случае игра заканчивается. • В случае объявления угрозы 2 -й игрок (СССР) в свою очередь стоит перед выбором – демонтировать ракеты, чтобы избежать ядерного конфликта, или защищать свою первую военную базу вне территории СССР всеми средствами. • После этого выбора игра заканчивается и определяются выигрыши игроков. Москва-2008

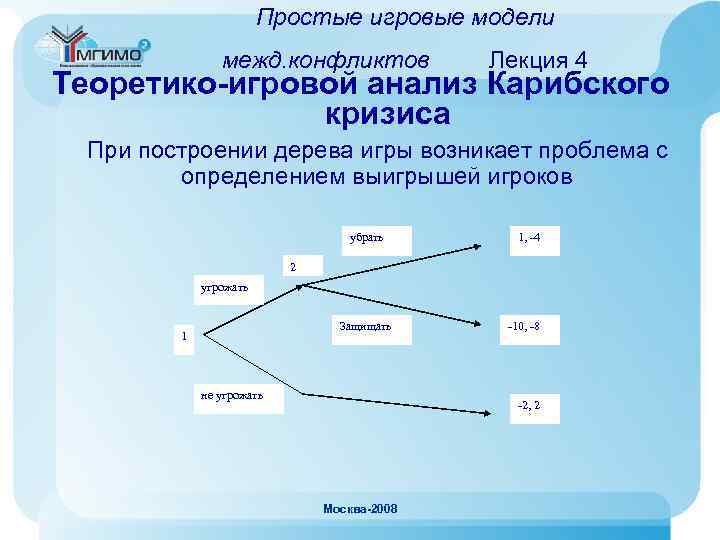Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса При построении дерева игры возникает проблема с определением выигрышей игроков убрать 1, -4 2 угрожать Защищать 1 не угрожать -10, -8 -2, 2 Москва-2008

Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса • В случае отказа США от противодействия развертыванию базы СССР получал военное и политическое преимущество. Поэтому выигрыши игроков условно можно оценить как (-2, 2). • В случае принятия решений о военном противостоянии с обоих сторон произошел бы ядерный конфликт - проиграли бы оба игрока. По мнению американцев, у США проигрыш был бы больше, т. к. население СССР было больше готово к новой войне после Второй мировой войны. Поэтому при таком исходе игры вектор выигрышей равен (-10, -8). • При согласии СССР убрать ракеты после угрозы со стороны США усиливалось военное превосходство Москва-2008 США и причинялся сильный ущерб международному

Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса НО! • Имея такую интерпретацию развития событий, Советский Союз не стал бы с самого начала разворачивать ракеты на Кубе, так как модель однозначно свидетельствует о выгодности выбора США в пользу угрозы и последующего выбора СССР по ликвидации базы без военного противоборства. • Т. е. модель слишком упрощенно описывает ситуацию. • Кризис не был игрой только двух лиц. И на одной, и на другой стороне на решения влияли большие команды (коалиции), входящие в них политики имели разные взгляды и даже самостоятельно участвовали в переговорах с лицами из другой коалиции, то есть Москва-2008 одновременно были игроками в нескольких играх.

Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса • Правильнее говорить, что существовала определенная вероятность р жесткой позиции советского руководства и вероятность (1 - р) мягкой позиции. • Известно, что Кеннеди оценивал вероятность ядерного конфликта (по сути она же и вероятность жесткой позиции р) величиной в интервале от 1/3 до 0. 5. • При жесткой позиции СССР изменяются выигрыши в модели – проигрыш в случае вывода ракет становится сильнее, а в случае защиты ракет и ядерного противостояния – меньше ( «лучше смерть, чем поражение» ). Москва-2008

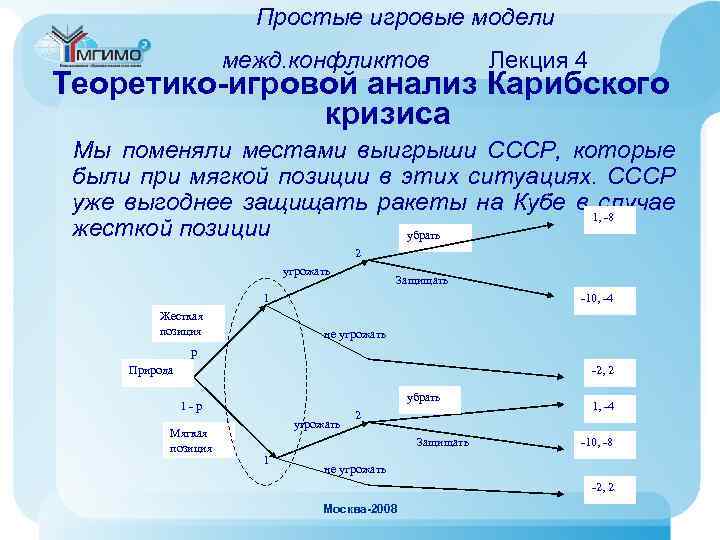Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса Мы поменяли местами выигрыши СССР, которые были при мягкой позиции в этих ситуациях. СССР уже выгоднее защищать ракеты на Кубе в 1, случае -8 жесткой позиции убрать 2 угрожать Защищать 1 Жесткая позиция -10, -4 не угрожать р Природа -2, 2 убрать 1 -р Мягкая позиция угрожать 2 Защищать 1 1, -4 -10, -8 не угрожать -2, 2 Москва-2008

Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса Оценим выигрыш США при объявлении угрозы СССР: В случае жесткой позиции СССР при угрозе со стороны США их проигрыш составит -10. В случае мягкой позиции СССР выведет ракеты и тогда выигрыш США составит +1. Т. е. , в зависимости от величины вероятности р средний выигрыш США составит: -10*р + 1*(1 – р) = 1 – 11 р При отказе США от угрозы ее выигрыш составит -2. Сравним два выигрыша, потому что США стоит прибегать к угрозе в том случае, когда первый выигрыш больше второго: Москва-2008 1 – 11 р > -2

Простые игровые модели межд. конфликтов Лекция 4 Теоретико-игровой анализ Карибского кризиса Таким образом, неравенство для вероятности: р < 3/11 Т. е. при р < 0. 27 руководство США не должно угрожать СССР и смирится с размещением ракет на Кубе. Почему же тогда Кеннеди прибег к угрозе, ведь по его мнению р>1/3 (условие р < 0. 27 не выполнялось)? -С такой точностью выигрыши оценить на деле не удается. При проигрыше США в случае войны величиной -100, угрожать им надо только при р < 0. 03. -Если выигрыши действительно такие, как в нашем случае, то угрожать можно, но надо сделать проигрыш США в случае войны меньше (смягчить Москва-2008 угрозу)

Простые игровые модели межд. конфликтов Лекция 4 Применение вероятной угрозы • При моделировании конфликтов используется понятие дозированной угрозы. Уменьшение угрозы при этом достигается за счет введения вероятности реализации угрозы q. То есть угроза состоит в том, что война будет с заданной вероятностью q. • Соответственно, проигрыш США в случае войны будет не -10, а -10*q, то есть меньше по модулю (ведь q < 1). В случае, если войны не будет, - цифры проигрыша тоже поменяются – вместо -2 он составит -2*(1 -q). • Средний же выигрыш США в случае применения такой вероятной угрозы будет: -10*q – 2*(1 – q) = -2 -8 q Москва-2008

Простые игровые модели межд. конфликтов Лекция 4 Применение вероятной угрозы Аналогично показывается, что у СССР при жесткой позиции и защите ракет выигрыш составит: -4*q + 2(1 – q) = 2 – 6 q. При мягкой позиции СССР и защите ракет получим: -8 q + 2(1 – q) = 2 – 10 q. Изобразим эти выражения в виде графа, где вместо угрозы используем термин brinkmanship, означающий в отличие от простой угрозы применение дозированной угрозы, которая реализуется с контролируемой вероятностью q. Москва-2008

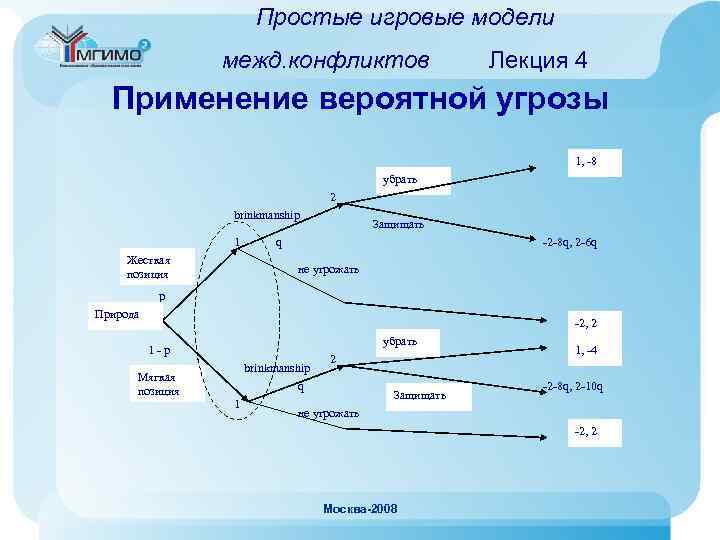Простые игровые модели межд. конфликтов Лекция 4 Применение вероятной угрозы 1, -8 убрать 2 brinkmanship 1 Жесткая позиция Защищать q -2 -8 q, 2 -6 q не угрожать р Природа -2, 2 убрать 1 -р Мягкая позиция brinkmanship 2 q 1 Защищать 1, -4 -2 -8 q, 2 -10 q не угрожать -2, 2 Москва-2008

Простые игровые модели межд. конфликтов Лекция 4 Применение вероятной угрозы ВЫВОДЫ: • При жесткой позиции СССР защита ракет при любом q выгоднее для СССР, ведь всегда -8 < 2 – 6 q. • При мягкой позиции советского руководства вывод ракет будет иметь место при -4 > 2 – 10 q, то есть при q > 0. 6. • Это условие эффективности угрозы. Оно означает, что США надо применять угрозу войны с вероятностью не менее 60%, или тогда вообще не угрожать. • Реализация вероятной угрозы в данном случае состоит в том, что после принятия СССР решения защищать ракеты, США используют датчик Москва-2008 случайных чисел. В этом смысле это чисто

Простые игровые модели межд. конфликтов Лекция 4 Применение вероятной угрозы Оценка приемлемого для США риска возникновения войны: Вычислим средний выигрыш США при объявлении дозированной угрозы с учетом вероятностей жесткой и мягкой позиций в СССР: (-2 – 8 q)*p + 1*(1 -p) = -8 pq -3 p + 1 Мягкая позиция соответствует выводу ракет. В случае отказа от угрозы выигрыш США составит -2. Поэтому применение угрозы выгодно для США при: -8 pq – 3 p +1 > -2. Получаем неравенство q < 0. 375(1/p – 1). Москва-2008

Простые игровые модели межд. конфликтов Лекция 4 Применение вероятной угрозы Оценка приемлемого для США риска возникновения войны: • Выражение q = 0. 375(1/p – 1) называется условием приемлемости угрозы. Анализ соответствующей функции q(p), графиком которой является гипербола, показывает, что вероятную угрозу здесь надо применять, если р лежит в интервале (0. 27, 0. 38). • При меньших р применима простая угроза (q = 1), а при р > 0. 38 любая эффективная угроза (q > 0. 6) оказывается неприемлемой для США, то есть им следует отказаться даже от вероятной угрозы (при р=0. 38 функция q(p) равна 0. 6 и потом убывает с ростом р). Москва-2008

Простые игровые модели межд. конфликтов Лекция 4 Применение вероятной угрозы Применение Brinkmanship на практике • Во время Карибского кризиса оценки вероятности р и выигрышей обоих сторон были весьма приближенными, что не позволяло рассчитать необходимую величину q и сделать вывод о целесообразности применения угрозы. • В момент самого конфликта всегда есть возможность скрининга, позволяющего опытным путем определить интересующие параметры. • В случае brinkmanship эффективность заданного уровня угрозы проверяется по реакции противника. Т. е. если начать с малого значения q и потом постепенно его увеличивать, то при соблюдении условия приемлемости угрозы при определенном Москва-2008 значении q вторая сторона конфликта примет ваши

Простые игровые модели межд. конфликтов Лекция 4 Применение вероятной угрозы Применение Brinkmanship на практике • В Карибском кризисе заявление Дж. Кеннеди о возможном объявлении морской блокады Кубы соответствует малому значению q порядка 0. 02. • Реальное введение блокады – это уже увеличение q. • Дальнейшему увеличению q способствовала бы утечка информации о готовящемся воздушном этапе по ракетной базе. • Процесс нарастания угрозы продолжался до тех пор, пока СССР не принял условия США. Это оказалось возможным, потому что выполнялось неравенство р < 0. 38. • В противном случае угроза рано или поздно стала бы слишком опасной Москва-2008 для США и им пришлось бы

Простые игровые модели межд. конфликтов Лекция 4 Применение вероятной угрозы Применение Brinkmanship на практике На практике контролировать точное значение q невозможно: 1. Наличие человеческого фактора (у людей есть нервы и подчиненные не точно выполняют приказания). 2. Возможны случайные события, когда резкое увеличение q может привести к реальной войне. 3. По мере нарастания угрозы можно потерять контроль над ситуацией и даже в случае принятия ваших условий противником ситуацию не удастся ввести в мирное русло. Поняв это, противник уже не будет уступать – он скажет, что от вас уже ничего не Москва-2008 зависит и договариваться с вами не о чем. Это

Лекция 5 Игры с неполной информацией и дезинформацией Содержание лекции 5 1. Виды неопределенностей. Роль точности оценки выигрышей 2. Игры с сигнализацией и дезинформацией. 3. Экстенсивные формы представления игры с учетом неопределенности. Москва-2008

Игры с неполной информацией и дезинформацией Лекция 5 Виды неопределенностей. Роль точности оценки выигрышей Виды неопределенностей (виды игр): • Статистическая неопределенность – азартные игры, игры «на счастье» (от франц. hasard – случай) • Комбинаторные игры - игрок стоит перед выбором из огромного числа вариантов ходов, которые он не в силах просчитать, поэтому в какой-то мере случайно выбирает ход (шахматы) • Стратегическая неопределенность – стратегические игры - неопределенность создает сам выбор той или иной стратегии противником Москва-2008

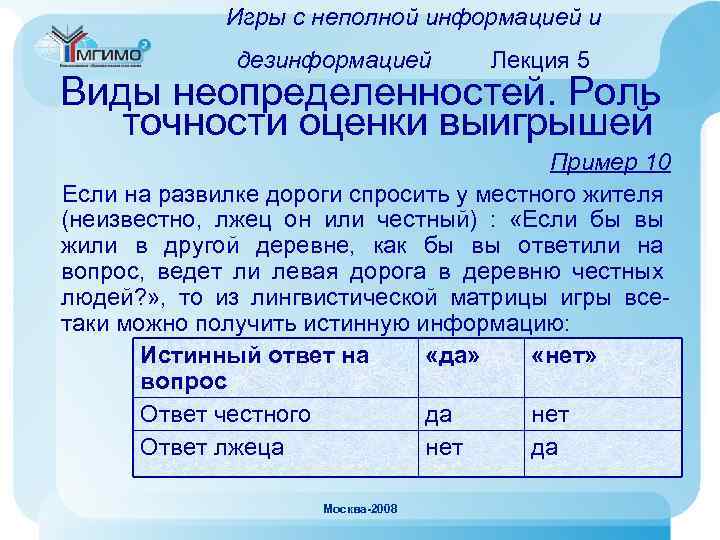Игры с неполной информацией и дезинформацией Лекция 5 Виды неопределенностей. Роль точности оценки выигрышей Пример 10 Если на развилке дороги спросить у местного жителя (неизвестно, лжец он или честный) : «Если бы вы жили в другой деревне, как бы вы ответили на вопрос, ведет ли левая дорога в деревню честных людей? » , то из лингвистической матрицы игры всетаки можно получить истинную информацию: Истинный ответ на «да» «нет» вопрос Ответ честного да нет Ответ лжеца нет да Москва-2008

Игры с неполной информацией и дезинформацией Лекция 5 Виды неопределенностей. Роль точности оценки выигрышей Пример 10 НО! Это верно только в том случае, если лжец всегда обманывает. Используют термин стратегический лжец для обозначения человека, который обманывает только тогда, когда это ему выгодно, создавая стратегическую неопределенность Москва-2008

Игры с неполной информацией и дезинформацией Лекция 5 Виды неопределенностей. Роль точности оценки выигрышей • Неопределенность в игре может быть связана с неточной информацией о значениях элементов матрицы игры (погрешность) • Лингвистические переменные - информация о выигрыше при разных стратегиях настолько скудная, что вместо чисел для элементов матрицы используют переменные типа «мало» , «много» , «очень много» • Если точность, с которой известны элементы матрицы игры, достаточна для определения максимума или минимума в строках и столбцах матрицы (а значит и седловой точки, если она есть), то уже можно определить оптимальный набор Москва-2008 стратегий

Игры с неполной информацией и дезинформацией Лекция 5 Виды неопределенностей. Роль точности оценки выигрышей • Для вычисления цены игры достаточно знать только элемент матрицы в седловой точке. • В каждом случае имея числовую матрицу игры и зная возможную погрешность ее элементов можно проверить устойчивость решения к вариациям элементов матрицы в пределах погрешностей. • Такие вариации обычно задают случайным образом с помощью датчика случайных чисел. Москва-2008

Игры с неполной информацией и дезинформацией Лекция 5 Игры с сигнализацией и дезинформацией • Игрок А обладает некой информацией, неизвестной игроку В. В этой связи у него 3 возможные стратегии поведения: • скрыть информацию, • передать игроку В всю информацию или ее часть, • дать противнику неверную информацию (дезинформацию, блеф – в карточных играх) Москва-2008

Игры с неполной информацией и дезинформацией Лекция 5 Роль блефа • В своей монографии «Теория игр и экономическое поведение» Нейман рассматривает роль блефа в покере • Он отмечает, что без блефа в принципе нельзя выиграть большую сумму даже при очень хорошем раскладе карт. • Для достижения такого выигрыша необходимо многократное повышение ставок и если противник будет знать, что вы никогда не блефуете, он уже после первых повышений поймет, что у вас хорошие карты и не станет дальше повышать свои • Если вы все время блефуете с плохими картами, противник потребует уже в начале игры раскрыть карты. Москва-2008 • Т. е. для получения большого выигрыша необходимо

Игры с неполной информацией и дезинформацией Лекция 5 Сигнализация • В играх с нулевой суммой (играх с постоянной суммой) выгодно скрыть информацию об очередном ходе, чтобы противник не мог ответить стратегией оптимального ответа. • При смешанных стратегиях для этого используют рандомизацию, то есть выбор очередной чистой стратегии с помощью датчика случайных чисел. На практике чаще просто скрывают информацию. • В то же время в других случаях выгоднее дать знать противнику о своих возможностях, чтобы избежать его нападения. Такое дозированное распространение выгодной для данного игрока информации называется сигнализацией. • Демонстрация новой военной техники на парадах – это пример сигнализации Москва-2008

Игры с неполной информацией и дезинформацией Лекция 5 Сигнализация • У менее информированного игрока В при получении информации от игрока А тоже есть 3 стратегии: • поверить этой информации, • не верить и пытаться отделить правду от лжи, Москва-2008 • игнорировать полученную информацию.

Игры с неполной информацией и дезинформацией Лекция 5 Сигнализация • Принято больше доверять информации, проявляющейся в действиях игрока А, чем его словам. • Зная это, игрок А может имитировать соответствующие действия с целью обмана • Игроку В необходимо предпринять действия, заставляющие игрока А обнаружить его истинные намерения и возможности. Такую стратегию называют скринингом • Примеры скрининга - у военных - разведка боем; у партизан - «проверки на дорогах» подозрительного новобранца, «если друг оказался вдруг и не враг, а так» - альпинизм (по В. Высоцкому, «парня в Москва-2008 горы тяни, рискни» )

Игры с неполной информацией и дезинформацией Лекция 5 Сигнализация • Выделяют также стратегию типа побудительной схемы (incentive scheme), при которой противника заставляют проявить своими действиями истинную информацию с помощью штрафов или поощрений • Примеры: • - библейская притча про царя Соломона, рассудившего, кому из двух женщин принадлежит ребенок (приказал разрезать) • - выплата большой премии по результатам работы, что заставляет работника полностью проявить его способности • - В международных отношениях - инспекции на ядерных объектах Ирана – если бы он обладал Москва-2008 атомной бомбой, ему пришлось бы отказать в

Игры с неполной информацией и дезинформацией Лекция 5 Экстенсивные формы представления игры с учетом неопределенности • Если в игре присутствует статистическая неопределенность (например значение одного из элементов матрицы игры известно как вероятностная величина), то в развернутой форме игры этому соответствует введение дополнительной точки принятия решения. • В отличие от точки, где выбор стратегии делает реальный игрок, эту точку называют точкой случая или точкой выбора природы. • Соответствующий кружок не штрихуется и возле него не ставится номер игрока. • Стрелками, выходящими из него, изображают возможные «случайные стратегии» , причем рядом с Москва-2008 ними указывают значение случайного параметра и

Игры с неполной информацией и дезинформацией Лекция 5 Экстенсивные формы представления игры с учетом неопределенности Пример 11 Рассмотрим в качестве примера парную игру с ненулевой суммой, которая в нормальной форме задана матрицей: 1/2 С D A x, 9 3, 6 B 6, 0 6, 9 Москва-2008

Игры с неполной информацией и дезинформацией Лекция 5 Экстенсивные формы представления игры с учетом неопределенности Пример 11 • У каждого игрока по 2 стратегии: у 1 -го - А и В, у 2 -го - С и D. • Выигрыш 1 -го игрока при комбинации стратегий АС задан случайным числом х. • Пусть про него известно, что с вероятностью 1/3 оно равно 0 и с вероятностью 2/3 оно равно 10. • Допустим, что 1 -й игрок при выборе своей стратегии знает, какое значение х на самом деле имеет место, тогда как 2 -й не знает этого. • Тогда игра в развернутом виде представляется следующим графом (см. рисунок). Пунктир соответствует отсутствию информации о 1 -м игроке у Москва-2008 2 -го игрока:

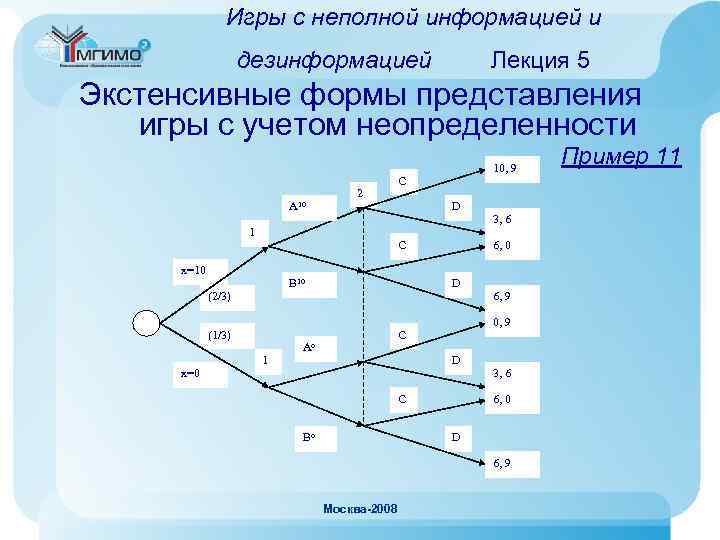Игры с неполной информацией и дезинформацией Лекция 5 Экстенсивные формы представления игры с учетом неопределенности A 10 2 1 C D C х=10 B 10 (2/3) (1/3) х=0 10, 9 1 6, 0 D D C Bo 6, 9 0, 9 C Ao 3, 6 6, 0 D 6, 9 Москва-2008 Пример 11

Игры с неполной информацией и дезинформацией Лекция 5 Экстенсивные формы представления игры с учетом неопределенности Пример 11 • Данная игра является асимметричной по информации, так как первый игрок обладает информацией о величине х до выбора своей стратегии, а второй – не знает. У первого игрока 4 стратегии: • - выбирать при х = 0 стратегию А, и при х = 10 – стратегию А (стратегия А 10 А 0); • - выбирать при х = 0 стратегию А, а при х = 10 – стратегию В (стратегия В 10 А 0); • - выбирать при х = 0 стратегию В, а при х = 10 – стратегию А (стратегия А 10 В 0); • - выбирать при х = 0 стратегию В, и при х = 10 – стратегию В (стратегия В 10 В 0); Москва-2008

Игры с неполной информацией и дезинформацией Лекция 5 Экстенсивные формы представления игры с учетом неопределенности Пример 11 • В обычной нормальной форме игра принимает вид матрицы размерности 4 х2. • Такая матрица называется нормальной формой по Байесу, потому что значения ее элементов рассчитываются по правилу Байеса для вычисления среднего значения вероятностных величин. • Например, элемент, соответствующий набору стратегий В 10 А 0 и D вычисляется с учетом вероятностей реализации разных значений параметра х следующим образом: (2/3)*(6, 9) + (1/3)*(3, 6) = (5, 8) (В скобках через запятую указаны компоненты Москва-2008 вектора выигрышей игроков)

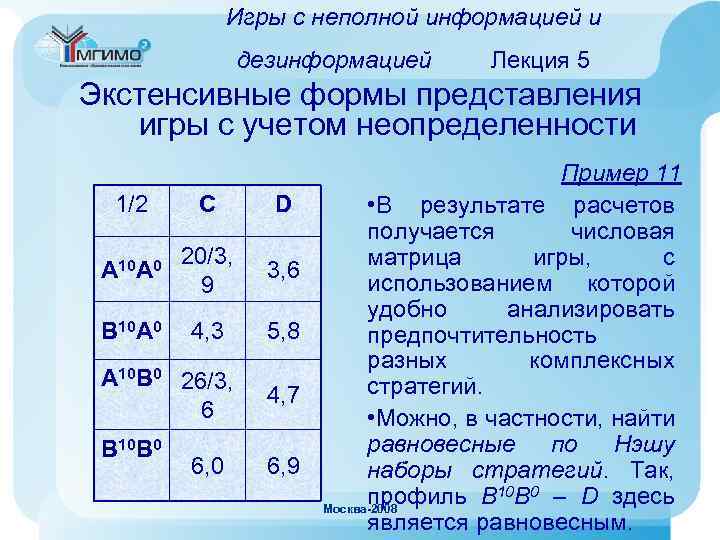Игры с неполной информацией и дезинформацией Лекция 5 Экстенсивные формы представления игры с учетом неопределенности 1/2 С D А 10 А 0 20/3, 9 3, 6 B 10 А 0 4, 3 5, 8 A 10 B 0 26/3, 6 B 10 B 0 6, 0 4, 7 6, 9 Пример 11 • В результате расчетов получается числовая матрица игры, с использованием которой удобно анализировать предпочтительность разных комплексных стратегий. • Можно, в частности, найти равновесные по Нэшу наборы стратегий. Так, профиль В 10 В 0 – D здесь Москва-2008 является равновесным.

Игры с неполной информацией и дезинформацией Лекция 5 Экстенсивные формы представления игры с учетом неопределенности Пример 11 • Вместо случайной величины х теперь в матрицу входят математические ожидания выигрыша с учетом вероятности различных значений х. Аналогичный подход используется для построения дерева решений в случае, когда решения принимает только одна сторона и известны вероятности их последствий. Это позволяет, в частности, учесть риски при реализации разных стратегий. Пример 12 • У лица, принимающего решение, (ЛПР) есть 2 варианта действий. В первом случае он может получить 10 тыс. у. е. с вероятностью 50%, а во втором – 20 тыс. с вероятностью 10%. Москва-2008

Игры с неполной информацией и дезинформацией Лекция 5 Экстенсивные формы представления игры с учетом неопределенности Пример 12 • Чтобы сделать правильный выбор, необходимо найти математические ожидания выигрыша в обоих случаях и сравнить их. • Это «ожидание» рассчитывается как произведение вероятности на величину выигрыша. • Первому варианту соответствует 0, 5*10000 = 5000 у. е. • Второму варианту 0, 1*20000 = 2000 у. е. • Первый вариант предпочтительней (5000>2000) Москва-2008

Лекция 6 Динамические модели переговоров Содержание лекции 6 1. Проблемы переговоров и их игровая интерпретация 2. Стандартное решение «договорной» игры (bargaining) 3. Ультимативные игры 4. Представление динамики переговоров игрой в развернутой форме Москва-2008

Динамические модели переговоров Лекция 6 Проблемы переговоров и их игровая интерпретация • До сих пор – анализ статических игр (одноходовых), которые можно представить в нормальной форме. • Предельный случай - игра, когда у каждого игрока по одной стратегии, которая состоит в том, чтобы ничего не делать. • НО! • С помощью таких игр можно анализировать возможные результаты переговоров, а не их процесс. • При отсутствии договоренностей стороны имели доход d 1 и d 2, а в случае заключения договора их доход станет v 1 v 2, причем di < v Москва-2008 i.

Динамические модели переговоров Лекция 6 Проблемы переговоров и их игровая интерпретация • Разница vi – di - величина уступки, которая более заинтересованная сторона может предложить менее заинтересованной для подписания договора. • Аналог ситуации с заключением контракта, когда в случае отказа от сотрудничества, то есть расторжения договора, сторона-инициатор расторжения выплачивает другой стороне определенную договором компенсацию α. • При отсутствии договора стороны тоже могут сотрудничать, если это им выгодно, но контракт повышает устойчивость такого сотрудничества. Москва-2008

Динамические модели переговоров Лекция 6 Проблемы переговоров и их игровая интерпретация • С точки зрения классической теории игр это парная игра 2 х2, стратегиями игроков является участие в договоре или отказ от него. • Пусть 1 -я стратегия – участие в сотрудничестве, 2 -я стратегия – разрыв договорных отношений. • При отсутствии контракта матрица игры имеет простую структуру: v 1, v 2 d 1, d 2 2 Москва-2008

Динамические модели переговоров Лекция 6 Проблемы переговоров и их игровая интерпретация Введением обязательных компенсационных платежей α и β контракт изменяет как минимум 2 элемента этой матрицы и она принимает вид: v 1, v 2 d 1+α, d 2α d 1 -β, d 2+β d 1, d 2 Москва-2008

Динамические модели переговоров Лекция 6 Проблемы переговоров и их игровая интерпретация • Появляется возможность подкорректировать матрицу и добиться существования устойчивости по Нэшу в точке а 11 (или повышения этой устойчивости) ПОЭТОМУ! • Желательно присутствие в договоре нескольких корректирующих параметров (α и β в нашем случае) • Это возможность оптимизировать ситуацию по строкам и столбцам для каждого игрока • Нередко используют, например, третий параметр, описывающий компенсационные выплаты при выходе сразу обеих сторон из договора Москва-2008

Динамические модели переговоров Лекция 6 Проблемы переговоров и их игровая интерпретация • При ведении переговоров решаются схожие проблемы взаимных уступок. • Примем те же условные обозначения. • При заключении договора создается новая ценность, стоимость которой равна: ΔV = v 1+v 2 - d 1 -d 2. • Эту сумму необходимо разделить между высокими договаривающимися сторонами в определенной пропорции, что должно служить основным предметом переговоров. Москва-2008

Динамические модели переговоров Лекция 6 Проблемы переговоров и их игровая интерпретация • Если вновь созданная ценность окажется преимущественно в распоряжении 1 -й стороны, то логично говорить о некоторой компенсации t, которая 1 -я сторона должна предложить 2 -й. • Тогда после подписания договора 1 -я сторона будет иметь v 1 - t, а вторая v 2+ t. • Помимо условий равновесия Нэша должны выполняться условия v 1 - t > d 1 и v 2+ t > d 2, определяющие т. н. точку несогласия. • В этой точке в результате заключения соглашения одна из сторон не получает какого-либо преимущества по сравнению с ситуацией, имевшей место до начала переговоров. Москва-2008 • Соответственно, у ней нет стимула к достижению

Динамические модели переговоров Лекция 6 Стандартное решение «договорной» игры (Bargaining) Стандартное решение обычной «договорной» игры состоит в следующем: • Определяются доходы сторон, которые они будут иметь после заключения договора в зависимости от тех или иных условий. • Желательно сформулировать эту зависимость от условий путем задания функций v 1(х) и v 2 (х), где х – переменная, описывающая ситуацию. Например х – это объемы поставок или таможенный тариф. • Определяется область возможных изменений величины х и находится такое ее значение, при котором суммарный доход договаривающихся сторон будет максимальный Москва-2008

Динамические модели переговоров Лекция 6 Стандартное решение «договорной» игры (Bargaining) • После фиксирования оптимального значения х оценивается новая ценность ΔV, которая создается при заключении договора для этого значения х. • При этом учитываются доходы (или убытки) сторон d 1 и d 2 на момент подписания договора. • Остается определить, как разделить ΔV между партнерами. Обозначим долю первого партнера π1, долю второго π2. Ясно, что π1 + π 2 = 1 и оба эти параметра принадлежат интервалу [0, 1]. Москва-2008

Динамические модели переговоров Лекция 6 Стандартное решение «договорной» игры (Bargaining) С учетом значений πi выигрыши сторон после заключения договора составят: U 1 = d 1 + π1ΔV U 2 = d 2 + π2ΔV Матрица «договорной» игры принимает вид: U 1, U 2 d 1+α, d 2–α d 1–β, d 2+β d 1, d 2 Москва-2008

Динамические модели переговоров Лекция 6 Стандартное решение «договорной» игры (Bargaining) • α и β – компенсационные выплаты в случае расторжения договора в одностороннем порядке (объявление дефолта) • Значения параметров π1, π2, α и β определяются в комплексе не только с учетом политического «веса» сторон, но и из соображений достижения устойчивости по Нэшу в точке а 11. • В связи с этим U 1 должно быть существенно больше d 1– β и U 2 – существенно больше d 2–α. • Для заключения договора необходимо выполнение еще более сильных неравенств: U 1 > d 1 U 2 > d , Москва-2008 2 определяющих точки несогласия.

Динамические модели переговоров Лекция 6 Стандартное решение «договорной» игры (Bargaining) • После достижения договоренности по долям π1 и π2 определяются компенсации t, которые одна сторона обязуется выплачивать другой в случае заключения договора. • Данная сумма равна модулю разности U 1 - v 1, то есть она полностью определяется оптимальным значением параметра х и согласованным значением доли π1. • В тексте договора будет стоять именно значение величины t наряду с параметром х. • Чтобы понять впоследствии, на каких долях π1 и π2 сошлись договаривающиеся стороны, придется Москва-2008 делать обратный пересчет.

Динамические модели переговоров Лекция 6 Ультимативные игры ДО СИХ ПОР! • Игры, в которых сам процесс переговоров не моделируется. • Не имеет значение, кто из игроков делает первый ход, то есть кто вносит предложение о параметрах договора. • Стандартное решение такой игры не зависит от последовательности поступления предложений от партнеров • Предложения принимаются или отклоняются только исходя из обсуждаемых значений таких параметров, как d 1, d 2, α и β. НО! В динамических Москва-2008 моделях переговоров

Динамические модели переговоров Лекция 6 Ультимативные игры Пример 13 • Между покупателем и продавцом дома происходят переговоры. • Пусть ценность дома для покупателя составляет 100 тыс. долларов, а для продавца 50 тыс. долл. • Разница между оценками стоимости объекта разными договаривающимися сторонами встречается достаточно часто (особенно по предметам культурной и исторической ценности) • Допустим, что переговоры состоят в том, что одна из сторон называет цену, а вторая либо соглашается с ней, либо отказывается от покупки-продажи. • В рассматриваемой нами ситуации каждая сторона согласна на цену в интервале от 50 до 100 Москва-2008 тыс. долларов.

Динамические модели переговоров Лекция 6 Ультимативные игры Пример 13 Стратегиями игроков здесь является с одной стороны предлагаемая цена, а с другой – согласие или отказ: Если это будет продавец, то он назовет 100 тыс. долл. (при условии, если ему известна оценка дома покупателем) и покупатель согласится, ведь он при этом ничего не теряет. То есть это будет равновесная по Нэшу цена, устраивающая обе стороны. • Если первым цену называет покупатель, то он назовет 50 тыс. долл. и это тоже будет равновесие по Нэшу, потому что эта цена максимально устраивает обе стороны в новых условиях. • Т. е. результат переговоров в данном случае зависит не только от оценки стоимости объекта сторонами, то есть от значения элементов матрицы выигрышей, но и Москва-2008 от самой процедуры переговоров, от их регламента

Динамические модели переговоров Лекция 6 Ультимативные игры • В классической теории игр - игроки выбирают свою стратегию одновременно и независимо друг от друга. • В ультимативных играх - в ряде случаев игроки делают свой выбор в разные моменты времени, причем результат игры зависит от последовательности, в которой игроки принимают решение. • 2 -й игрок при этом делает выбор, уже зная выбор первого игрока. • Бывают случаи, когда игроки принимают решение совместно, а не по одиночке – так происходит при подписании договоров, контрактов, вступающих в силу лишь после того, как все стороны поставили свои подписи. Москва-2008

Динамические модели переговоров Лекция 6 Представление динамики переговоров игрой в развернутой форме • Точки принятия решения отдельными игроками изображаются на нем обычными черными точками с указанием номера игрока рядом с ней. • Выбор определенной стратегии отображается стрелкой. • Точкам принятия совместных решений сразу несколькими игроками соответствуют точки, обведенные кружком. • Если стратегией игрока является выбор определенного значения из заданного интервала чисел, то это отображается сектором дугой между двумя отрезками, выходящими из точки принятия Москва-2008 решения.

Динамические модели переговоров Лекция 6 Представление динамики переговоров игрой в развернутой форме • Выбору стратегии соответствует точка дуги, из которой выходит стрелки, описывающие стратегии другого игрока. • Над сектором указывают обозначение параметра, выбор значения которого осуществляется первым игроком. • Возле стрелок, соответствующих концу игры, указываются через запятую выигрыши каждого игрока. Именно так изображаются, например, те же ультимативные игры. Москва-2008

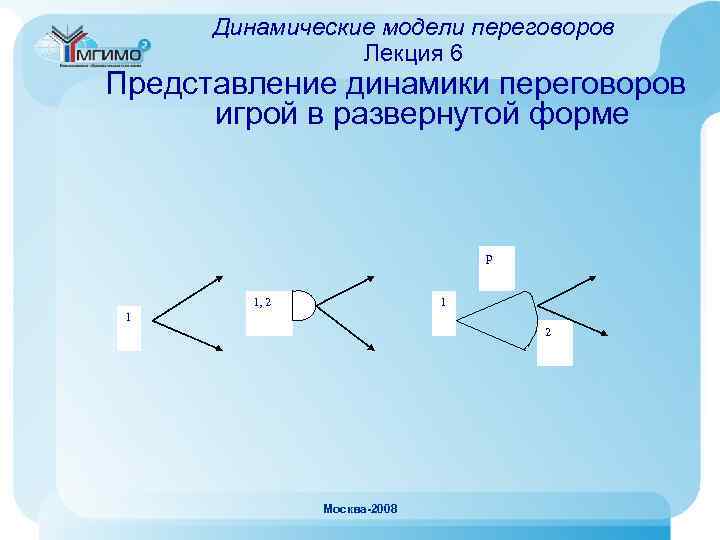Динамические модели переговоров Лекция 6 Представление динамики переговоров игрой в развернутой форме р 1, 2 1 1 2 Москва-2008

Динамические модели переговоров Лекция 6 Представление динамики переговоров игрой в развернутой форме • Различные комбинации таких элементов образуют достаточно сложный граф, отображающий ход переговоров. • Такое представление удобно для количественного анализа последствий отдельных решений, сделанных в ходе переговоров. • Выбрав наиболее выгодный конечный вариант по величине выигрыша, приведенной в конце графа, можно методом обратной индукции определить всю последовательность оптимальных решений в ходе переговоров. Москва-2008

Лекция 7 Применение теории игр к анализу выборов и голосования в коллективных органах Содержание лекции 7 1. Игры на оптимальное размещение (location games). 2. Приложение к оптимизации предвыборной платформы. 3. Учет политического спектра избирателей. Москва-2008

Теория игр для анализа выборов и голосования Лекция 7 Игры на оптимальное размещение (location games). Пример 14 • 2 продавца прохладительных напитков устанавливают свои палатки на пляже, разделенном на 9 секторов, последовательно пронумерованных. В каждом секторе одинаковое количество потенциальных покупателей, причем каждый из них покупает воду в ближайшей к нему палатке, а если они одинаково близки – то половина людей из этого сектора пляжа покупает в одной, половина – в другой. • В каком секторе продавцу установить палатку, если второй может свою поставить хоть где, даже Москва-2008 в одном секторе с ним?

Теория игр для анализа выборов и голосования Лекция 7 Игры на оптимальное размещение (location games). Пример 14 • Ситуации соответствует парная игра, в которой у каждого игрока по 9 стратегий (номер стратегии соответствует номеру сектора пляжа, где он поставит палатку). • Матрица игры имеет размерность 9 х9. • Будем выражать выигрыш 1 -го продавца в числе секторов пляжа, откуда отдыхающие придут к нему. • Если оба продавца ставят палатки в один и тот же сектор пляжа, то независимо от номера сектора они получат одинаковый выигрыш. Поэтому на главной диагонали матрицы стоят одинаковые числа 9/2 = 4, 5 Москва-2008

Теория игр для анализа выборов и голосования Лекция 7 Игры на оптимальное размещение (location games). Пример 14 • Такой же выигрыш будет при симметричном расположении продавцов относительно середины пляжа (то есть в 1 -м и 9 -м секторах, 2 -м и 8 -м, 3 -м и 7 м, 4 -м и 6 -м). • Если 1 -й продавец ставит палатку в первом секторе, а 2 -й – во втором, то к 1 -му придут отдыхающие только с первого сектора, то есть а 12 = 1. • Если 1 -й ставит в первом секторе, а 2 -й - в 3 -м, то к 1 му обратятся люди из первого и половины второго сектора, то есть а 13 = 1, 5. Соответственно а 14 = 2, а 15 = 2, 5, а 16 = 3, а 17 = 3, 5, а 18 = 4 и а 19 = 4, 5. Москва-2008

Теория игр для анализа выборов и голосования Лекция 7 Игры на оптимальное размещение (location games). Пример 14 • Приступаем к заполнению второй строки матрицы. • Если первый продавец ставит палатку во втором секторе, а второй – в первом, то к первому обратится 8 секторов, поэтому а 21 = 8. • И так далее. • В результате получим следующую матрицу выигрышей 1 -го игрока Москва-2008

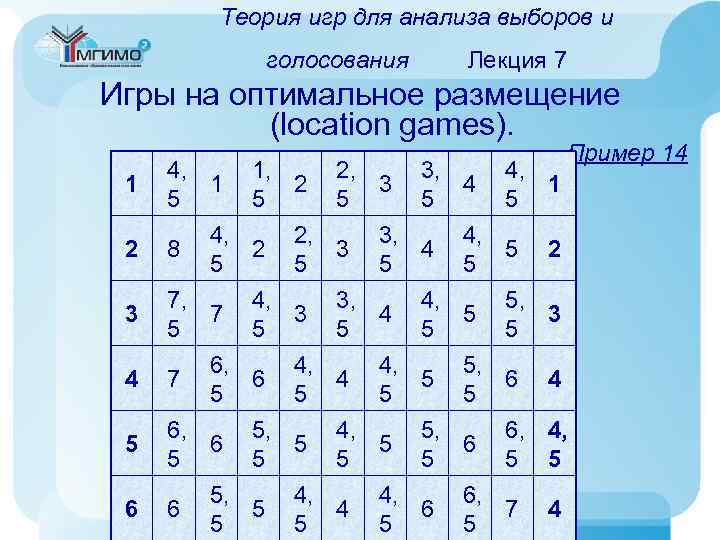Теория игр для анализа выборов и голосования Лекция 7 Игры на оптимальное размещение (location games). 1 4, 1 5 4, 2 5 2 8 3 7, 7 5 4 7 5 6, 6 5 6 6 1, 2 5 2, 3 5 4, 3 5 6, 6 5 3, 4 5 4, 4 5 5, 5 5 2, 3 5 4, 5 5 2 5, 3 5 5, 6 5 4, Москва-2008 4, 4 6 5 5 4, 1 5 Пример 14 4 6, 4, 5 5 6, 7 5 4

Теория игр для анализа выборов и голосования Лекция 7 Игры на оптимальное размещение (location games). Пример 14 • Видно, что минимаксной стратегией здесь является пятая. Установив палатку в 5 -м секторе (то есть посередине пляжа) 1 -й продавец гарантирует себе выигрыш 4, 5 независимо от того, где поставит палатку 2 -й продавец. • У 2 -го игрока тоже оптимальной является 5 -я стратегия. • Если один из игроков придерживается такой стратегии, а другой – нет, то последний получает меньше, чем 4, 5. • Это игра с ненулевой суммой (биматричная) и Москва-2008 поэтому необходимо отдельно рассматривать еще и

Теория игр для анализа выборов и голосования Лекция 7 Игры на оптимальное размещение (location games). Пример 14 • Обычно обе матрицы совмещают в виде одной со сдвоенными элементами, но в данном случае это будет слишком громоздко. • Номерам стратегий 2 -го игрока соответствуют номера столбцов, поэтому матрица 2 -го игрока здесь получается из матрицы 1 -го транспонированием, например ее первая строка будет такой же, как первый столбец исходной. • У 2 -го игрока тоже оптимальной является 5 -я стратегия. Если 1 -й избрал рекомендованную стратегии, а 2 -й – нет, то выигрыш 1 -го может только увеличиться (до 6, 5), а. Москва-2008 выигрыш второго будет всегда

Теория игр для анализа выборов и голосования Лекция 7 Игры на оптимальное размещение (location games). Пример 14 • Для упрощения работы по заполнению матрицы необходимо выявить закономерности • Например, достаточно вычислить лишь первые 5 строк – остальные их повторяют в обратном порядке (последняя – первую, предпоследняя – вторую и т. д. ). • Элементы матрицы 2 -го игрока можно сразу вычислять как разность между 9 и соответствующим элементом первой матрицы. • Потому, что выигрыши игроков жестко связаны, рассмотренная игра относится к сильно конкурентным играм, которые по сути близки к Москва-2008 антагонистическим

Теория игр для анализа выборов и голосования Лекция 7 Оптимизация предвыборной платформы Пример 15 Два кандидата борются за голоса избирателей в округе, причем спектр политических предпочтений избирателей очень широк. Его можно разделить на 9 интервалов ( «левые» , «умеренные» и т. д. ). Для простоты будем считать, что на каждый такой интервал приходится по 10000 избирателей. На какой политический спектр нужно сделать ставка? • Аналог задачи про пляж. Элементы в игровой матрице надо умножить на 10000 – и можно подсчитывать голоса в зависимости от выбранной точки на политическом спектре • Это инструмент для моделирования исходов выборов Москва-2008 в зависимости от заявленной платформы каждого

Теория игр для анализа выборов и голосования Лекция 7 Оптимизация предвыборной платформы Пример 15 а В Примере 15 проведите анализ шансов на победу в выборах 1 -го кандидата в предположении, что для 2 го кандидата равновероятен любой интервал политического спектра. • Вероятное число голосов, которое получит 1 -й кандидат, придерживающийся i-го интервала спектра, в этом случае равно среднему значению элементов i-ой строки • Элементы полученной ранее матрицы выражают собой число голосов, поданных за первого кандидата, в единицах 10 тыс. голосов. • Необходимо сложить элементы каждой строки и Москва-2008 разделить сумму на 9 (число интервалов политического

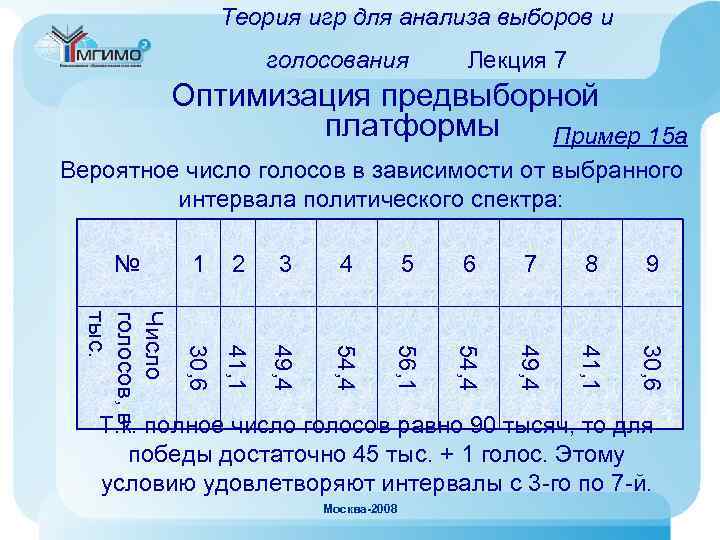Теория игр для анализа выборов и голосования Лекция 7 Оптимизация предвыборной платформы Пример 15 а Вероятное число голосов в зависимости от выбранного интервала политического спектра: 41, 1 49, 4 6 7 8 9 30, 6 5 41, 1 Число голосов, в тыс. 4 49, 4 3 54, 4 2 56, 1 1 54, 4 № Т. к. полное число голосов равно 90 тысяч, то для победы достаточно 45 тыс. + 1 голос. Этому условию удовлетворяют интервалы с 3 -го по 7 -й. Москва-2008

Теория игр для анализа выборов и голосования Лекция 7 Оптимизация предвыборной платформы Пример 15 б Обобщим модель голосования (пример 15 а) на случай неравномерного политического спектра избирателей. Зададим в 6 и 7 интервалах большее число избирателей, чем в других. Пусть в этих интервалах будет по 15000 избирателей, а в остальных – по прежнему по 10000. • В этом случае придется пересчитать матрицу выигрышей, имея в виду, что «статистический вес» выделенных секторов стал 1, 5. • Симметрии теперь не наблюдается (хотя на главной диагонали по прежнему оба кандидата делят голоса пополам). Москва-2008

Теория игр для анализа выборов и голосования Лекция 7 Оптимизация предвыборной платформы Пример 15 б • Поскольку полное число голосов теперь равно 100 тысяч, то матрицу игры можно представить в форме отклонения набранных голосов от «законных» 50 тысяч, что соответствует игре с нулевой суммой. • В данном случае матрица является кососимметричной, то есть зеркально симметричной относительно главной диагонали с точностью до знака (он разный у симметричных элементов). • Игры с матрицей такого типа называются симметричными. • Элементы матрицы равны числу избыточных или недостающих голосов (в тысячах) по сравнению с половиной всех голосов при разных наборах чистых Москва-2008 стратегий кандидатов.

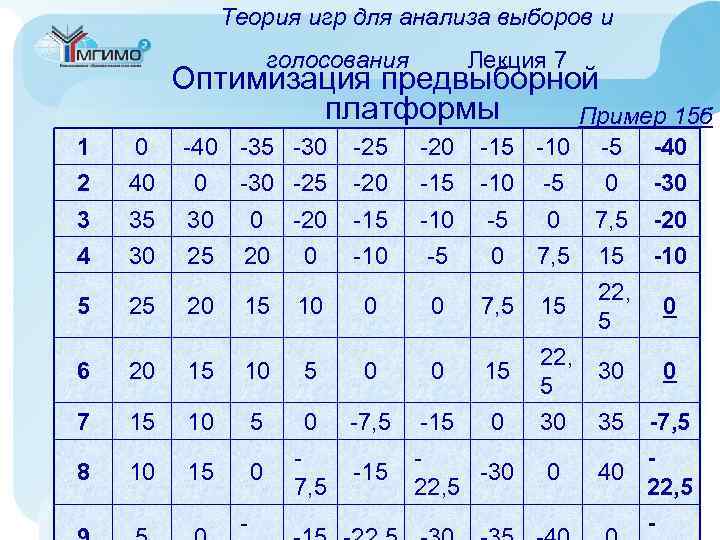Теория игр для анализа выборов и голосования Лекция 7 Оптимизация предвыборной платформы Пример 15 б 1 0 -40 -35 -30 2 40 0 3 35 30 0 4 30 25 20 -25 -20 -15 -10 -5 -40 -20 -15 -10 -5 0 -30 -20 -15 -10 -5 0 7, 5 -20 0 -10 -5 0 7, 5 15 -10 0 -30 -25 5 25 20 15 10 0 0 7, 5 15 22, 5 6 20 15 10 5 0 0 15 22, 5 30 0 7 15 10 5 0 -7, 5 -15 0 30 35 -7, 5 0 7, 5 -15 -30 22, 5 0 40 22, 5 8 10 15 - Москва-2008 -

Теория игр для анализа выборов и голосования Лекция 7 Оптимизация предвыборной платформы Пример 15 б • Анализ с нахождением максимального минимума по строкам и минимального максимума по столбцам дает, что игра имеет 4 седловые точки, то есть решается в чистых стратегиях • Обоим кандидатам следует придерживаться 5 -го или 6 -го интервалов спектра. При этом им гарантируется по 50% голосов. • Подобная теоретико-игровая модель дает прогноз с разумной точностью и от ее нельзя требовать результатов расчетов с погрешностью в один голос из 100000 поданных голосов. Москва-2008

Теория игр для анализа выборов и голосования Лекция 7 Учет политического спектра избирателей • Игровая модель может использоваться и в случае, когда предпочтения избирателей (политический спектр) заданы некоторой функцией. • При этом достаточно провести аппроксимацию непрерывной функции гистограммой, искусственно разбив весь спектр на определенное число интервалов. • В каждом из интервалов может быть любое число голосов избирателей, в том числе, например, разное во всех интервалах. • Обычно используется однопиковая функция, определенная на отрезке [0, 1] оси Х одномерного политического пространства. Точка xи, на которую приходится максимум этой функции, называется идеальной. Москва-2008

Теория игр для анализа выборов и голосования Лекция 7 Учет политического спектра избирателей • Левый склон пика соответствует избирателям левого толка, правый – правого. Например, применяют функцию вида: f(x) = a + b│x - xи│, • где a и b – численные коэффициенты, задающие общее число избирателей и крутизну пика. Рассмотренный выше пример с равномерным спектром соответствует значению b=0. • Идеальная точка может располагаться и на границе области определения, тогда спектр имеет вид обычной линейной функции. Москва-2008

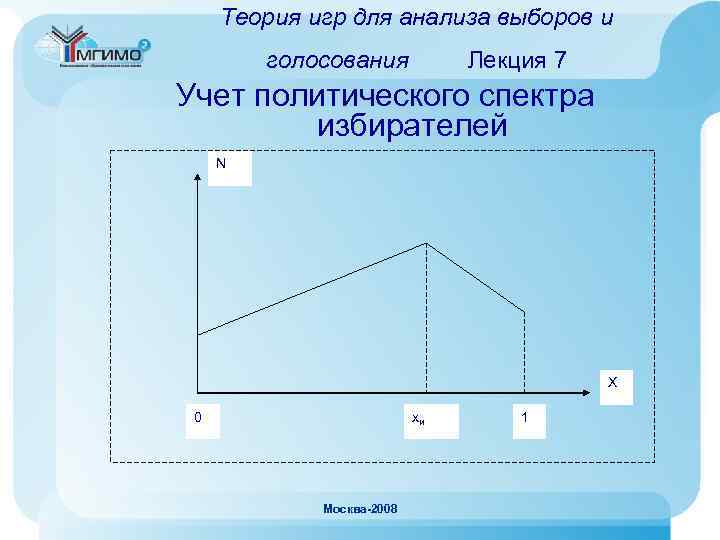Теория игр для анализа выборов и голосования Лекция 7 Учет политического спектра избирателей N X 0 хи Москва-2008 1

Теория игр для анализа выборов и голосования Лекция 7 Учет политического спектра избирателей • После разбивки отрезка [0, 1] на интервалы количество избирателей в каждом из них определяется значением спектральной функции на середине интервала. • Т. к. в расчетах используется численная аппроксимация спектральной функции, то она может быть любой, в том числе многопиковой. Можно вообще задать ее сразу просто таблицей, составленной на основе социологических опросов. • Повторяем процедуру с составлением матрицы игры по аналогии с продавцами на пляже, число секторов которого равно теперь заданному числу интервалов. • Рекомендуется записать матрицу в форме отклонения от половины имеющихся голосов, после чего провести классический анализ для игр с нулевой Москва-2008 суммой.

Лекция 8 Модели конкуренции и оптимизации сотрудничества Содержание лекции 8 1. Модель лоббирования интересов двух сторон. 2. Учет партнерских интересов при максимизации личного выигрыша (partnership game). 3. Модели конкуренции при олигополии. Москва-2008

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модель лоббирования интересов двух сторон • Применительно к проблеме выборов из двух кандидатов существенное значение могут иметь затраты на предвыборную кампанию, которую можно рассматривать как «лоббирование» определенных политических позиций среди избирателей. • В этой связи рассмотрим теоретико-игровую модель лоббирования своих интересов двумя конкурирующими фирмами. • Поскольку при этом успех лоббирования конкретного проекта нередко зависит от поведения конкурирующей стороны, то есть все основания и здесь использовать в качестве модели парную игру. • Выигрышем для каждого игрока является потенциальная выгода, получаемая в случае успеха лоббирования, проигрыш же равен затраченным Москва-2008 ресурсам при победе конкурирующего проекта.

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модель лоббирования интересов двух сторон • Игры, описывающие лоббирование, по числу возможных стратегий у игроков относятся к бесконечным играм. НО! • Если учесть, что выбор вкладываемой в лоббирование суммы ограничен финансовыми возможностями игрока и эта сумма номинируется с разумной точностью (например, дискретами по 1000 евро), то игра становится конечной. Москва-2008

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модель лоббирования интересов двух сторон Пример 16 Пусть обе фирмы без лоббирования имеют одинаковый годовой доход P условных единиц. В случае успеха лоббирования выигравшая фирма получает доход S условных единиц, а проигравшая – N условных единиц, причем S>P и N

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модель лоббирования интересов двух сторон Пример 16 • В случае отказа от лоббирования и при отклонении предлагаемого проекта обе фирмы просто сохраняют прежний доход P и не терпят убытков. • С другой стороны, если фирма приняла решение лоббировать, а проект не прошел, итоговый «выигрыш» составит P – L. • Если прошел проект второй фирмы, то выигрыш первой в любом случае равен N. • Наконец, если фирма не принимала участие в лоббировании и ее проект был, тем не менее, принят, выигрыш составит S. Москва-2008

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модель лоббирования интересов двух сторон Пример 16 • Нормальная форма игры представлена в таблице. • Через запятую указаны выигрыши первой и второй фирм, когда вторая фирма не лоббирует свои интересы, а в таблице 2 – когда лоббирует. • При этом для простоты предполагалось, что в случае лоббирования одной из фирм один из проектов обязательно принимается, а при отказе обеих фирм от лоббирования или лоббировании обеими фирмами – оба отклоняются. • Могут быть и другие условия, например, допускаться отказ и при лоббировании одной фирмой. Формально это означает изменение правил игры, определяющих выигрыши сторон при определенном наборе их стратегий. Москва-2008

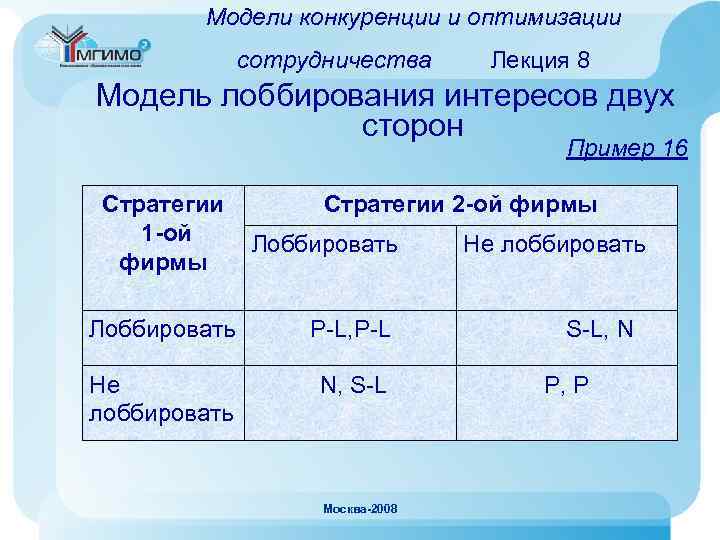Модели конкуренции и оптимизации сотрудничества Лекция 8 Модель лоббирования интересов двух сторон Пример 16 Стратегии 1 -ой фирмы Стратегии 2 -ой фирмы Лоббировать Р-L, Р-L Не лоббировать N, S-L Москва-2008 Не лоббировать S-L, N P, P

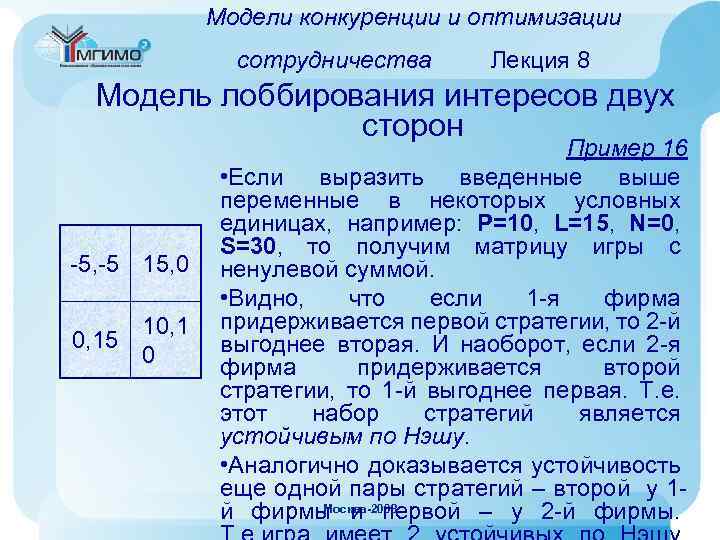Модели конкуренции и оптимизации сотрудничества Лекция 8 Модель лоббирования интересов двух сторон -5, -5 15, 0 0, 15 10, 1 0 Пример 16 • Если выразить введенные выше переменные в некоторых условных единицах, например: P=10, L=15, N=0, S=30, то получим матрицу игры с ненулевой суммой. • Видно, что если 1 -я фирма придерживается первой стратегии, то 2 -й выгоднее вторая. И наоборот, если 2 -я фирма придерживается второй стратегии, то 1 -й выгоднее первая. Т. е. этот набор стратегий является устойчивым по Нэшу. • Аналогично доказывается устойчивость еще одной пары стратегий – второй у 1 Москва-2008 й фирмы и первой – у 2 -й фирмы.

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модель лоббирования интересов двух сторон Пример 16 • В нашем примере если известно решение 2 -й фирмы, то 1 -й ясно что надо делать. А если известна лишь вероятность того или иного решения? • Считаем, что 2 -я фирма придерживается смешанной стратегии. Пусть известно, что вероятность лоббирования 2 -й фирмой равна р. Соответственно вероятность не лоббирования равна для нее (1 – р). • Доход 1 -й фирмы принятии решения о лоббировании составит в среднем -5 р + 15(1 - р) =15+20 р, а при не лоббировании – 0 +10(1 -р) = 10 10 р. • Эти расчеты выполняются сначала по первой, а потом по второй строке матрицы для 1 -й фирмы. Если приравнять полученные доходы, получим р = 0, 5. Поэтому при р>0, 5 1 -й. Москва-2008 в среднем выгоднее не фирме

Модели конкуренции и оптимизации сотрудничества Лекция 8 Учет партнерских интересов при максимизации личного Пример 17 выигрыша • Два лица сотрудничают, их совместный доход определяется вкладом каждого из них по формуле: f(е 1, е 2) = а 1 е 1 + а 2 е 2. • Здесь а 1 и а 2 – численные коэффициенты, а е 1 и е 2 – вклад каждого партнера в общее дело. • Этот доход делится между ними таким образом, что первый получает долю x<1, а второй – долю (1 х). • При этом считается, что себестоимость затрат каждого партнера оценивается как еi 2. Тогда чистый доход первого партнера равен: U 1 = t f(е 1, е 2) - е 12. • До какой степени 1 -му партнеру выгодно Москва-2008 увеличивать свой вклад?

Модели конкуренции и оптимизации сотрудничества Лекция 8 Учет партнерских интересов при максимизации личного Пример 17 выигрыша • Данную ситуацию можно моделировать парной игрой, в которой стратегиями игроков являются разные значения их вкладов. Получится большая числовая матрица, которую потом надо исследовать. НО! можно применить более эффективный в данном случае метод анализа, который, строго говоря, не имеет отношения к классической теории игр, использовать тот факт, что известна сама функция выигрыша, к которой можно применить обычный математический анализ, то есть исследовать зависимость функции U 1 от переменной е 1. • Это квадратичная зависимость, графиком которой является обращенная вниз парабола. Москва-2008

Модели конкуренции и оптимизации сотрудничества Лекция 8 Учет партнерских интересов при максимизации личного выигрыша Пример 17 U 1 е 1 0 e 0 Москва-2008

Модели конкуренции и оптимизации сотрудничества Лекция 8 Учет партнерских интересов при максимизации личного выигрыша Пример 17 • Для нахождения оптимального значения достаточно приравнять нулю производную ∂ U 1/∂ е 1. Отсюда получаем: t а 1 - 2 е 1 = 0 • Следовательно, оптимальный вклад первого партнера в совместное дело составляет t а 1/2. Получается, что он не зависит от вклада второго партнера, зато зависит от причитающейся по контракту доли общего дохода. • Аналогичным образом решаются задачи, в которых f(е 1, е 2) такова, что производная ∂ U 1/∂ е 1 зависит от вклада второго партнера е 2. Москва-2008

Модели конкуренции и оптимизации сотрудничества Лекция 8 Учет партнерских интересов при максимизации личного выигрыша Пример 17 • Пусть f(е 1, е 2) = а 1 е 1 + а 2 е 2 + 2 е 1 е 2 • В этом случае из условия равенства нулю производной ∂ U 1/∂ е 1. получим соотношение: t(а 1 +2 е 2) - 2 е 1 = 0. • После этого можно уже в терминах теории игр говорить, что полученное выражение определяет оптимальный ответ (BR) первого партнера (значения е 1) на известный вклад второго партнера е 2. • При t = 0/5 получим е 1 = (а 1 +2 е 2)/4, то есть наилучший вклад первого партнера растет пропорционально увеличению вклада второго партнера. В общем случае вид функций U 1(е 1, е 2) и f(е 1, е 2) определяется спецификой задачи. Москва-2008

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модели конкуренции при олигополии Пример 18 Модель конкуренции при дуополии (модель Курно) • Две независимые фирмы производят одну и ту же продукцию в объемах q 1 и q 2 и реализуют ее на одном рынке. Цена на эту продукцию в соответствии с законами экономики зависит от предложения товара и поэтому с увеличением объемов q 1 и q 2 уменьшается: Р = 1000 - q 1 - q 2 • Издержки производства составляют 100 q 1 и 100 q 2 соответственно. Результирующий доход первой фирмы через устанавливающуюся цену зависит от объема производства второй фирмы: U 1 = (1000 - q 1 - q 2) q 1 - 100 q 1. Москва-2008

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модели конкуренции при олигополии Пример 18 • Это модель взаимодействия двух сторон, в которой каждая сторона независимо выбирает свою стратегию – объем производства qi. • В этом случае также удобнее провести анализ функции выигрыша для определения оптимального ответа на известную стратегию второй стороны, а не выписывать матрицу игры. • Если раскрыть скобки в выражении для U 1, опять получим квадратичную функцию на этот раз от q 1. Она имеет того же типа график, что мы рассматривали применительно к предыдущей модели, только теперь по оси абцисс откладывается q 1. Остается найти точку максимума из условия равенства нулю производной: Москва-2008 -2 q 1 + (1000 - q 2 - 100) = 0

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модели конкуренции при олигополии Пример 18 • Оптимальное значение q 1 = 450 - q 2/2. • Задача симметрична относительно партнеров, поэтому в устойчивом состоянии оптимальный ответ у обеих фирм будет одинаков. • В этой связи равновесное состояние определяется уравнением типа BR(q 2) = q 2, которое в данном случае имеет вид: 450 - q 2/2 = q 2. • Его решение дает рекомендуемые объемы производства q 1 = q 2 = 300. Москва-2008 устойчивые

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модели конкуренции при олигополии • Даже независимые «игроки» в условиях рынка на самом деле оказываются тесно связанными и имеют весьма ограниченную степень свободы. К аналогичному выводу можно придти, рассматривая дуополию Бертрана, при которой каждая из двух фирм независимо устанавливает цену на свою продукцию и доход обеих сторон зависит от соотношения этих цен. • Можно привести пример аналогичных моделей и из области международных отношений. Рассмотрим, как меняется доход государства при изменении таможенной политики двух стран. Москва-2008

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модели конкуренции при олигополии Пример 19 • Пусть первая страна установила таможенную пошлину в размере x %, а вторая - y %. Доход первой страны от таможенных сборов с учетом уменьшения товарообмена при слишком высокой ставке таможенного налога можно выразить функцией выигрыша вида: U 1 (млрд. долл. ) = 2000 + 60 x + xy – x 2 – 80 y • Как и в случае с дуополией получили квадратичную функцию, определение максимума которой позволяет вычислить оптимальный ответ на повышение (понижение) таможенной пошлины второй страной. В качестве аргумента, по которому осуществляется максимизация функции U 1 (х), здесь рассматривается Москва-2008 таможенный тариф первой страны.

Модели конкуренции и оптимизации сотрудничества Лекция 8 Модели конкуренции при олигополии • Существуют также модели конкуренции, в которых взаимодействующие стороны представлены несимметрично. Это выражается в разных функциях выигрыша сторон. • Классическим примером является модель «преступление и наказание» , которая описывает взаимосвязь уровня законности в стране x и уровня преступности y. • Функция выигрыша государства при этом описывается соотношением: U 1 (x, y) = – c 4 x – y 2/x, • где с – затраты государства по усилению правопорядка в стране. • Для преступного же мира функция выигрыша существенно иная: Москва-2008 U 2 (x, y) = √y/(1 +xy)