Теория игр 7. Игра размера 2 х2.
Теория игр 2. Геометрический метод решения игры 2× 2. Пусть игрок А выбирает свою смешанную стратегию P={p 1, p 2}={p 1, 1 -p 1}, а игрок В чистую стратегию В 1. Тогда выигрыш игрока А есть: H(P, B 1) = Σpiai 1 = p 1 a 11+p 2 a 21=(1 -p)a 11+pa 21= = p(a 21 -a 11)+a 11 (6. 1) В системе координат (p, H) зависимость (6. 1) представляет собой отрезок прямой, заданный на отрезке [0, 1], проходящий через точки (0, а 11) и (1, а 21)
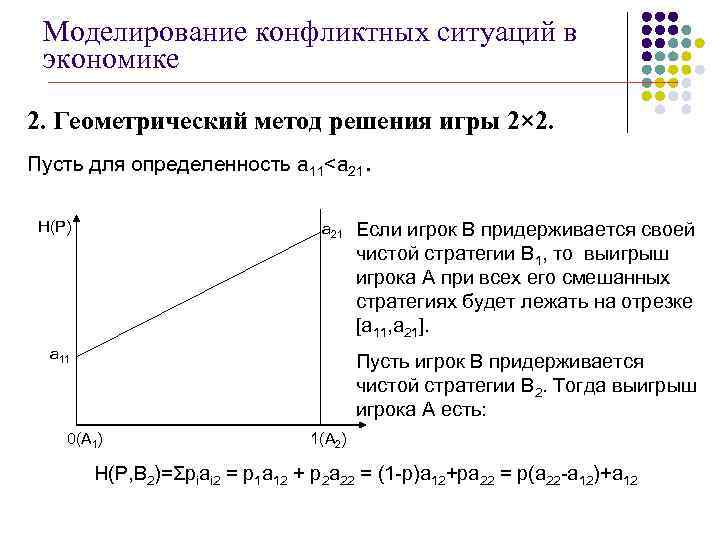Моделирование конфликтных ситуаций в экономике 2. Геометрический метод решения игры 2× 2. Пусть для определенность а 11<а 21. H(P) а 21 а 11 Если игрок В придерживается своей чистой стратегии В 1, то выигрыш игрока А при всех его смешанных стратегиях будет лежать на отрезке [a 11, a 21]. Пусть игрок В придерживается чистой стратегии В 2. Тогда выигрыш игрока А есть: 0(А 1) 1(А 2) H(P, B 2)=Σpiai 2 = p 1 a 12 + p 2 a 22 = (1 -p)a 12+pa 22 = p(a 22 -a 12)+a 12
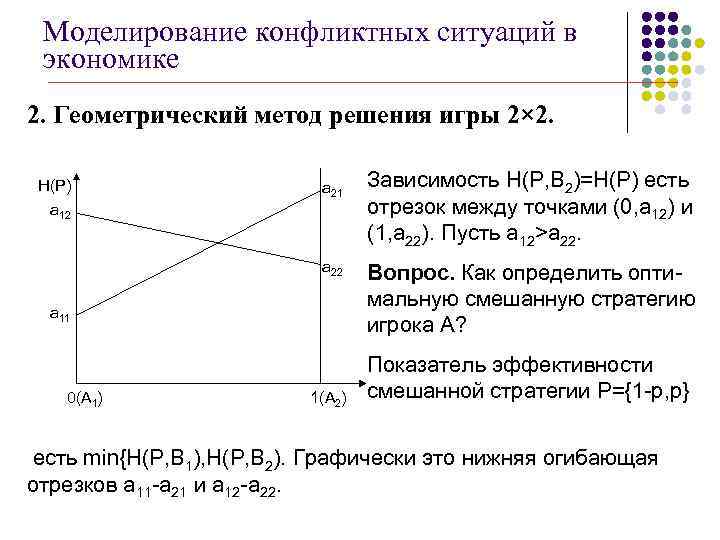Моделирование конфликтных ситуаций в экономике 2. Геометрический метод решения игры 2× 2. H(P) а 21 а 12 а 22 а 11 0(А 1) 1(А 2) Зависимость H(P, B 2)=H(P) есть отрезок между точками (0, a 12) и (1, a 22). Пусть а 12>а 22. Вопрос. Как определить оптимальную смешанную стратегию игрока А? Показатель эффективности смешанной стратегии P={1 -p, p} есть min{H(P, B 1), H(P, B 2). Графически это нижняя огибающая отрезков а 11 -а 21 и а 12 -а 22.
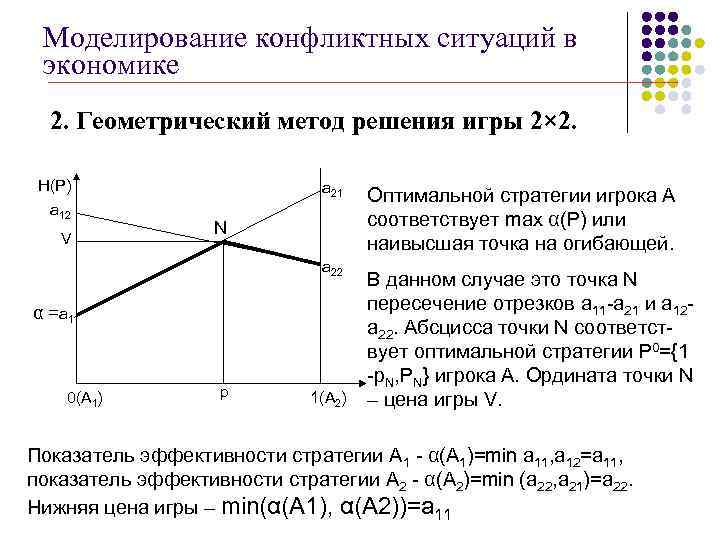Моделирование конфликтных ситуаций в экономике 2. Геометрический метод решения игры 2× 2. H(P) а 12 V а 21 N а 22 α =а 11 0(А 1) p 1(А 2) Оптимальной стратегии игрока А соответствует max α(P) или наивысшая точка на огибающей. В данном случае это точка N пересечение отрезков а 11 -а 21 и а 12 а 22. Абсцисса точки N соответствует оптимальной стратегии P 0={1 -p. N, PN} игрока А. Ордината точки N – цена игры V. Показатель эффективности стратегии А 1 - α(A 1)=min a 11, a 12=a 11, показатель эффективности стратегии А 2 - α(A 2)=min (a 22, a 21)=a 22. Нижняя цена игры – min(α(A 1), α(A 2))=a 11
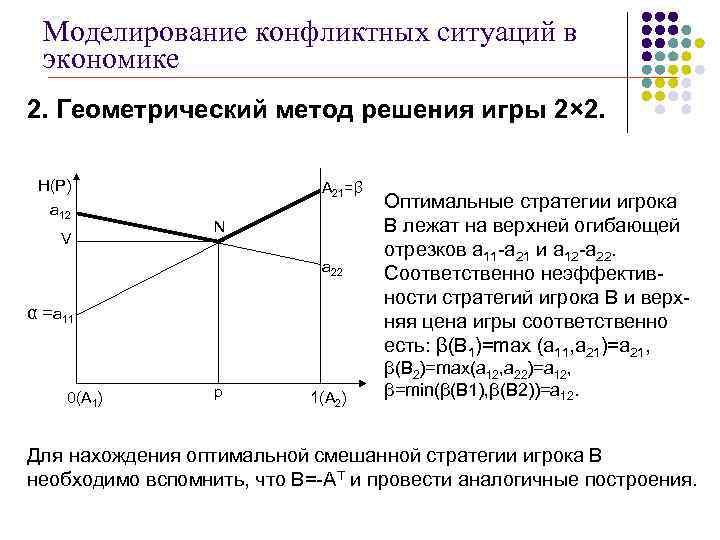Моделирование конфликтных ситуаций в экономике 2. Геометрический метод решения игры 2× 2. H(P) а 12 V А 21=β N а 22 α =а 11 0(А 1) p 1(А 2) Оптимальные стратегии игрока В лежат на верхней огибающей отрезков а 11 -а 21 и а 12 -а 22. Соответственно неэффективности стратегий игрока В и верхняя цена игры соответственно есть: β(В 1)=max (a 11, a 21)=a 21, β(В 2)=max(a 12, a 22)=a 12, β=min(β(В 1), β(В 2))=a 12. Для нахождения оптимальной смешанной стратегии игрока В необходимо вспомнить, что В=-АТ и провести аналогичные построения.
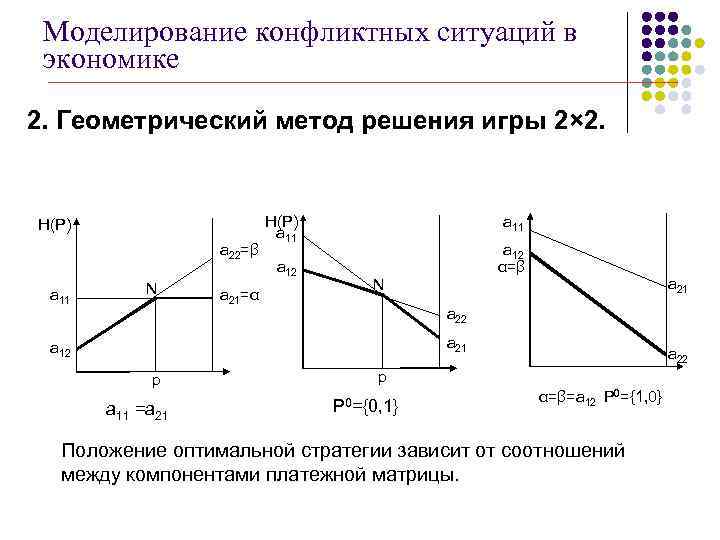Моделирование конфликтных ситуаций в экономике 2. Геометрический метод решения игры 2× 2. H(P) a 22=β а 11 N а 21=α H(P) а 11 а 12 α=β а 21 N a 22 а 21 а 12 p a 11 =a 21 a 22 p P 0={0, 1} α=β=a 12 P 0={1, 0} Положение оптимальной стратегии зависит от соотношений между компонентами платежной матрицы.
Моделирование конфликтных ситуаций в экономике 2. 1 Решение игры 2×N Игрок А имеет SA={A 1, A 2} Игрок В имеет SB={B 1, B 2, B 3, …, Bn} Тогда получим: H(P, B 1)=(1 -p)a 11+pa 21=p(a 21 -a 11)+a 11 H(P, B 2)=(1 -p)a 12+pa 22=p(a 22 -a 12)+a 12 H(P, Bn)=(1 -p)a 1 n+pa 2 n=p(a 2 n-a 1 n)+a 1 n Получаем N отрезков в координатах (р, Н), строим огибающую, ищем наивысшею точку на ней.
Моделирование конфликтных ситуаций в экономике 3. Аналитическое решение игры 2× 2. Рассмотрим случай, когда матрица игры не имеет седловой точки. Тогда решение можно получить исходя из геометрического решения. Имеем: H(P, B 1) = Σpiai 1 = p(a 21 -a 11)+a 11 (7. 3) H(P, B 2)=Σpiai 2 = p(a 22 -a 12)+a 12 (7. 4) Условие наличия цены игры V есть: H(P, B 1) = H(PB 2)
Моделирование конфликтных ситуаций в экономике 3. Аналитическое решение игры 2× 2. Приравняв выражения (7. 3) и (7. 4), получим уравнение, из которого легко вычислить значение р=Р 20: p(a 22 -a 12)+a 12 = p(a 21 -a 11)+a 11 или р(а 11+а 22 -а 12 -а 21)= а 11 -а 12 Откуда следует: р2 = р = 0 а 11 – а 12 (а 22 + а 11) – (а 12 + а 21) р1 = 1 -р = 0 а 22 – а 21 (а 22 + а 11) – (а 12 + а 21)
Моделирование конфликтных ситуаций в экономике 3. Аналитическое решение игры 2× 2. Соответственно для игрока В получим: H(Q, A 1)=q 1 a 11+q 2 a 12 = q(a 12 -a 11)+a 11 H(Q, A 2)=q 1 a 21+q 2 a 22 = q(a 22 -a 21)+a 21 Откуда следует: q 2 0 = q = a 11 – a 21 (а 22 + а 11) – (а 12 + а 21) V= q 10 =1 - q = a 11 a 22 – a 12 a 21 (а 22 + а 11) – (а 12 + а 21) a 22 – a 12 (а 22 + а 11) – (а 12 + а 21)
Моделирование конфликтных ситуаций в экономике 3. Аналитическое решение игры 2× 2. Вопрос. При каком условии справедливы полученные соотношения? Очевидно, когда знаменатель не равен 0. (а 22 + а 11) – (а 12 + а 21) ≠ 0 (7. 5) Равенство нулю выражения (7. 5) является необходимым условием наличия седловой точки в матрице игры.
Моделирование конфликтных ситуаций в экономике 4. Матричные игры и задачи линейного программирования. Между матричными играми и линейным программированием существует взаимосвязь, которая состоит в том, что решение любой матричной игры можно свести к решению пары двойственных задач линейного программирования специального вида и, наоборот, любая задача линейного программирования, которая имеет решение, может быть сведена к матричной игре специального вида.
Моделирование конфликтных ситуаций в экономике 4. Матричные игры и задачи линейного программирования. Теорема. Решение матричной игры m×n c матрицей А, элементы которой aij>0, эквивалентно решению следующей пары двойственных задач линейного программирования:
Моделирование конфликтных ситуаций в экономике 4. Матричные игры и задачи линейного программирования. Поясним теорему, опуская доказательство. Пусть имеем матрицу игры m×n. Оптимальная стратегия P={p 1, p 2, …, pm} обеспечивает ему выигрыш H(P, Q)≥ V. Если игрок В выбирает чистую стратегию Вj, то выигрыш игрока А есть: H(P, Bj)=Σaijpi=a 1 jp 1+a 2 jp 2+…+amjpm≥ V; Σpi = 1 Получим систему из n неравенств.
Моделирование конфликтных ситуаций в экономике (7. 6) Если V>0, то все неравенства можно разделить на V. Условие V>0 легко достигается путем прибавления к каждому элементу aij константы r>0. Эта операция приведет к смещению цены игры V на r, но не повлияет на выбор оптимальных стратегий.
Моделирование конфликтных ситуаций в экономике 4. Матричные игры и задачи линейного программирования. В результате получим: (7. 7)
Моделирование конфликтных ситуаций в экономике 4. Матричные игры и задачи линейного программирования. Вводя переменные x 1=p 1/v, x 2=p 2/v, … и, учитывая, что игрок А стремится получить максимальный выигрыш (V=>max или 1/v=>min), получим задачу линейного программирования для игрока А: (Аналогичные рассуждения приводят к двойственной задачи для игрока В) x 1+x 2+x 3+…+xm=>min a 11 x 1+a 21 x 2+…+am 1 xm ≥ 1 a 12 x 1+a 22 x 2+…+am 2 xm ≥ 1 y 1+y 2+y 3+…+yn=>max a 11 y 1+a 12 y 2+…+a 1 nyn ≤ 1 a 21 y 1+a 22 y 2+…+a 2 nyn ≤ 1 a 1 nx 1+a 2 nx 2+…+amnxm ≥ 1 am 1 y 1+am 2 y 2+…+amnyn ≤ 1 Решения этих задач позволяет найти оптимальные смешанные стратегии игроков А и В.
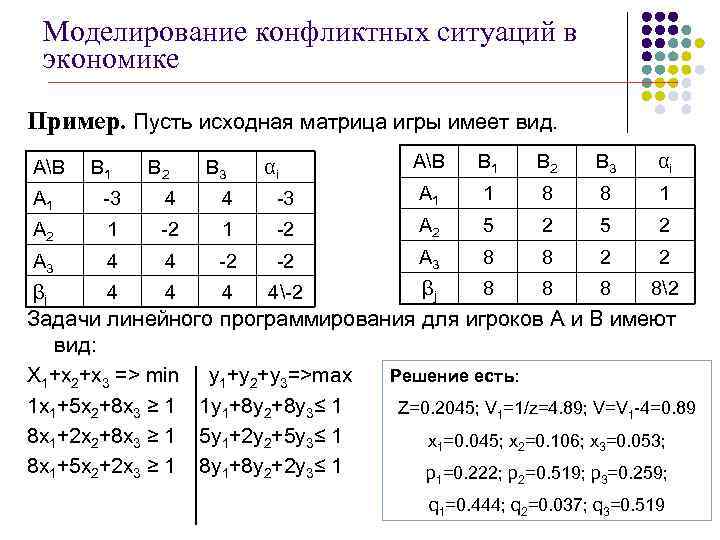Моделирование конфликтных ситуаций в экономике Пример. Пусть исходная матрица игры имеет вид. АВ В 1 В 2 В 3 αi А 1 -3 4 4 -3 А 1 1 8 8 1 А 2 1 -2 А 2 5 2 А 3 4 4 -2 -2 А 3 8 8 2 2 βj 4 4-2 βj 8 82 Задачи линейного программирования для игроков А и В имеют вид: Решение есть: Х 1+х2+х3 => min y 1+y 2+y 3=>max 1 x 1+5 x 2+8 x 3 ≥ 1 1 y 1+8 y 2+8 y 3≤ 1 Z=0. 2045; V 1=1/z=4. 89; V=V 1 -4=0. 89 8 x 1+2 x 2+8 x 3 ≥ 1 5 y 1+2 y 2+5 y 3≤ 1 x 1=0. 045; x 2=0. 106; x 3=0. 053; 8 x 1+5 x 2+2 x 3 ≥ 1 8 y 1+8 y 2+2 y 3≤ 1 p 1=0. 222; p 2=0. 519; p 3=0. 259; q 1=0. 444; q 2=0. 037; q 3=0. 519