Теория графов

Теория графов Набор – неупорядоченная система объектов из некоторого множества, в котором один и тот же объект может встречаться несколько раз Множество V={a 1, a 2, …} и набор E из неупорядоченных пар объектов из V называется графом G(V, E) a 1, a 2, … вершины графа ребра графа геометрическая реализация графа G(V, E) Связный граф, полный граф Компонента связности Изоморфные графы путь (маршрут) цикл - петля

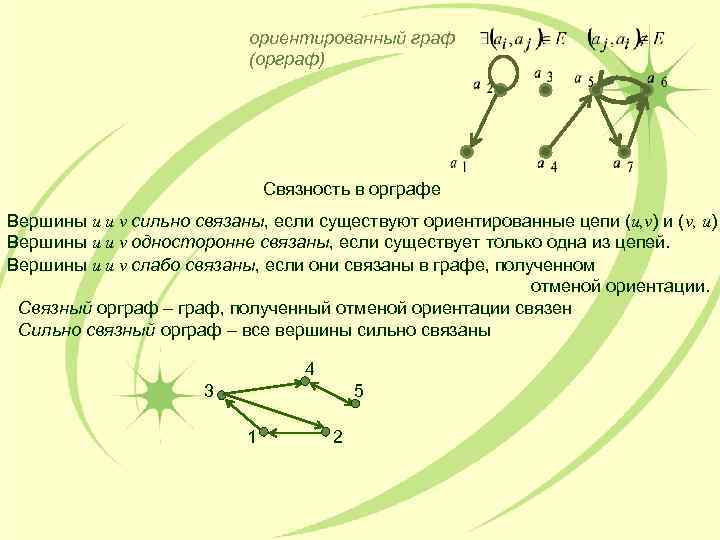
ориентированный граф (орграф) Связность в орграфе Вершины u и v сильно связаны, если существуют ориентированные цепи (u, v) и (v, u) Вершины u и v односторонне связаны, если существует только одна из цепей. Вершины u и v слабо связаны, если они связаны в графе, полученном отменой ориентации. Связный орграф – граф, полученный отменой ориентации связен Сильно связный орграф – все вершины сильно связаны 4 3 5 1 2

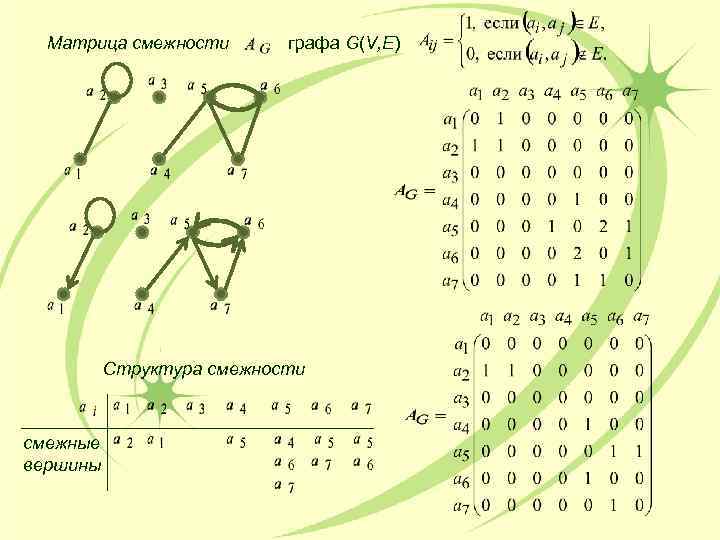
Матрица смежности графа G(V, E) Структура смежности смежные вершины

Матрица инцидентности графа G(V, E) 2 4 1 5 3 6 7 Список ребер графа - вершины исхода ребер - вершины входа ребер G(V, E) - реберно взвешенный граф матрица весов графа G(V, E) - вес маршрута

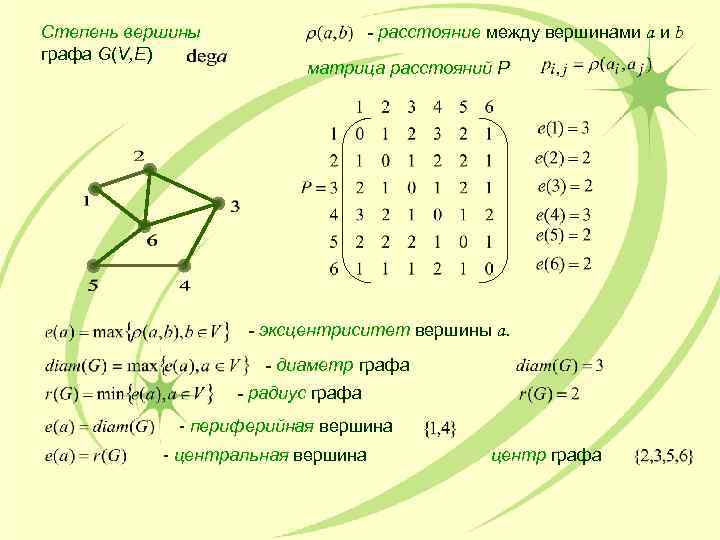
Степень вершины - расстояние между вершинами a и b графа G(V, E) матрица расстояний P - эксцентриситет вершины a. - диаметр графа - радиус графа - периферийная вершина - центральная вершина центр графа

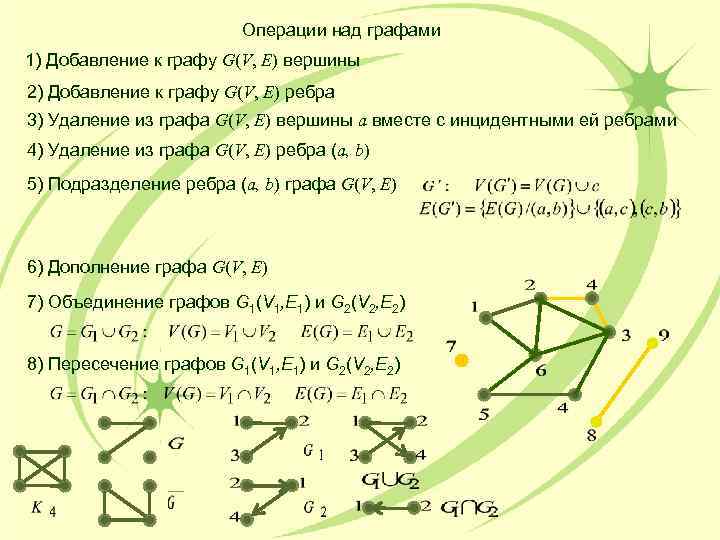
Операции над графами 1) Добавление к графу G(V, E) вершины 2) Добавление к графу G(V, E) ребра 3) Удаление из графа G(V, E) вершины a вместе с инцидентными ей ребрами 4) Удаление из графа G(V, E) ребра (a, b) 5) Подразделение ребра (a, b) графа G(V, E) 6) Дополнение графа G(V, E) 7) Объединение графов G 1(V 1, E 1) и G 2(V 2, E 2) 8) Пересечение графов G 1(V 1, E 1) и G 2(V 2, E 2)

9) Кольцевая сумма графов G 1(V 1, E 1) и G 2(V 2, E 2) 10) Соединение графов G 1(V 1, E 1) и G 2(V 2, E 2) 11) Произведение графов G 1(V 1, E 1) и G 2(V 2, E 2) 12) Подграфа G(V, E) 13) Часть графа G(V, E) 14) Композиция графов G 1(V 1, E 1) и G 2(V 2, E 2)

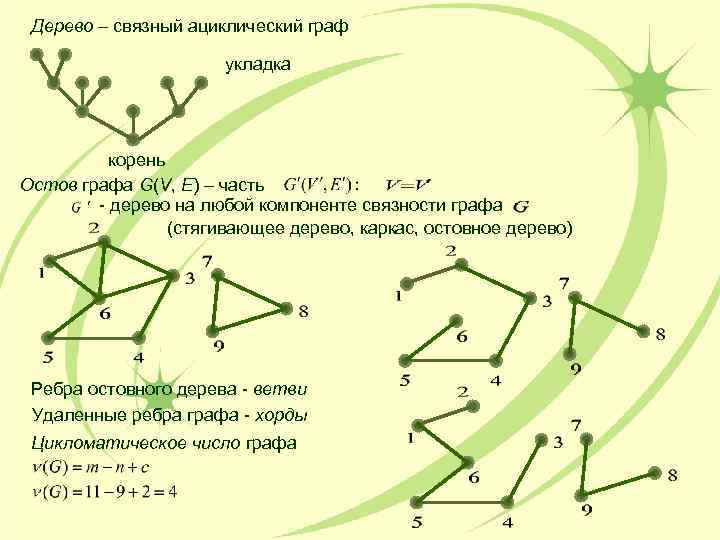
Дерево – связный ациклический граф укладка корень Остов графа G(V, E) – часть - дерево на любой компоненте связности графа (стягивающее дерево, каркас, остовное дерево) Ребра остовного дерева - ветви Удаленные ребра графа - хорды Цикломатическое число графа

Метод поиска в глубину 1) Начинаем с фиксированной вершины a 0. 2) Рассматриваем вершину, смежную выбранной, если их нет, то возвращаемся к предыдущей вершине. 3) Поиск заканчивается при возврате в a 0 и отсутствии смежных ей еще не рассмотренных вершин Метод поиска в ширину 1) Начинаем с фиксированной вершины a 0. 2) Рассматриваем все вершины, смежные выбранной.

Алгоритмы поиска остова минимального веса Алгоритм Краскала 1) Строим граф - ребро минимального веса i) Из графа строим - ребро минимального веса, не принадлежащее и не образующее циклов с его ребрами Алгоритм Прима Дерево строится добавлением ребер минимального веса, одна вершина которых принадлежит дереву, другая нет

Планарность Граф называется планарным, если изоморфен плоской геометрической интерпретации грани графа - внутренние, внешняя эйлерова характеристика планарного графа Граф К 5 – не планарный Граф К 3, 3 – не планарный Теорема Куратовского-Понтрягина. (Критерий плоской реализуемости). Граф G(V, E) планарен тогда и только тогда, когда он не содержит подграфов, подразделяющихся до К 5 и К 3, 3. Задача о трех домах и трех колодцах (Куратовский 1930 г. )

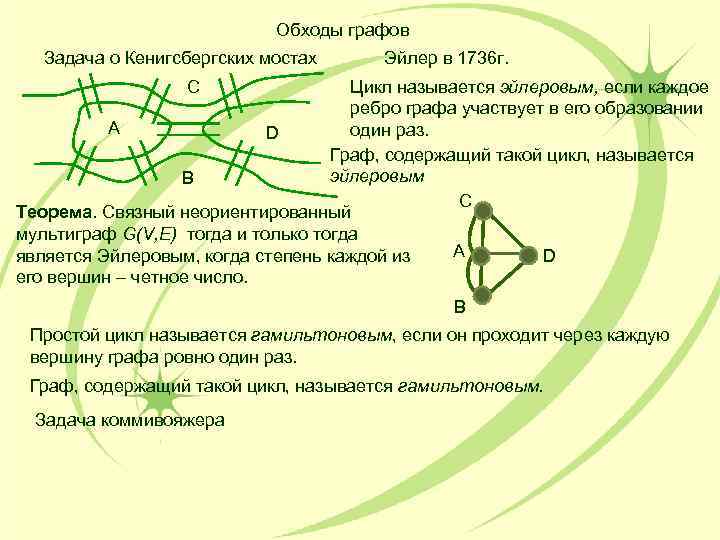
Обходы графов Задача о Кенигсбергских мостах Эйлер в 1736 г. C Цикл называется эйлеровым, если каждое ребро графа участвует в его образовании А D один раз. Граф, содержащий такой цикл, называется B эйлеровым C Теорема. Связный неориентированный мультиграф G(V, E) тогда и только тогда является Эйлеровым, когда степень каждой из А D его вершин – четное число. B Простой цикл называется гамильтоновым, если он проходит через каждую вершину графа ровно один раз. Граф, содержащий такой цикл, называется гамильтоновым. Задача коммивояжера

Раскраска вершин графов (для графов без петель) - вершинная k-раска графа G(V, E) Правильная k-раска -для смежных вершин u и v k – раскрашиваемый граф Хроматическое число графа G – минимальное число k, при котором G является k-раскрашиваемым Задача о раскрашивании карты (1879 г. А. Кэли) Гипотеза четырех красок: всякая карта 4 -раскрашиваема. Алгоритм последовательного раскрашивания 1) Выбираем вершину a 0 и красим в первый цвет. 2) Вершины a 0, a 1, …, ai, раскрашены p цветами: 1, 2, …p красим вершину ai+1 в минимальный цвет, не использованный при раске смежных вершин. (Для улучшения алгоритма выбираем вершину максимальной степени) 1 Задача расписания. Вершины – лекции. Смежные вершины – не читаются одновременно 2 3 Оптимальное расписание - минимальная раска { …} 4 5 6

Задача о раскрашивании ребер. 1 26 Монтаж аппаратуры: 2 3 Вершины – платы; Ребра - проводники 4 5 6 12 16 46 56 13 35