Теория формальных языков и трансляций Часть II Глава

Теория формальных языков и трансляций Часть II. Глава 1. Трансляции, их представление и реализация 1

Часть 2: Трансляции и синтаксические методы их реализации § 1. 1. Трансляции и трансляторы Определение 1. 1. Трансляцией из языка L 1 * в язык L 2 * называется отношение L 1 L 2. Здесь — входной алфавит, L 1 — входной язык, — выходной алфавит, L 2 — выходной язык. Другими словами, трансляция есть некоторое множество пар предложений (x, y), где x L 1 — входное, а y L 2 — выходное предложение. 2

Часть 2: Трансляции и трансляторы Хотя в общем случае в трансляции одному входному предложению x может соответствовать несколько выходных предложений y, по отношению к языкам программирования трансляция всегда является функцией, т. е. для каждого входа существует не более одного выхода. Существует бесконечно много примеров трансляций, но самым элементарным, вероятно, является тот, который может быть задан гомоморфизмом, т. е. отображением h из в *. 3

Часть 2: Трансляции и трансляторы Пример 1. 1. Предположим, что мы хотим закодировать некоторый текст с помощью азбуки Морзе. Как известно, в коде Морзе каждая буква представляется как некоторая последовательность из точек и тире. Эти последовательности, называемые посылками, имеют разную длину. Для отделения одной посылки от другой используется пауза. 4

Часть 2: Трансляции и трансляторы Очевидно, что трансляцию предложений, например, на русском языке, в код Морзе можно реализовать с помощью гомоморфизма, задаваемого следующим образом: Буква: а б в … я Посылка: . — — …. —. — Для простоты предполагаем, что паузы представлены пробелами, завершающими каждую посылку. Тогда, скажем, слово “абба” с помощью замены букв на посылки. — даёт результат: — …. — 5

Часть 2: Гомоморфизм Для любой входной цепочки x = a 1 a 2 … an, ai , i=1, 2, …, n, гомоморфизм h позволяет найти соответствующую выходную цепочку y * с помощью посимвольной подстановки: y = h(a 1)h(a 2)… h(an). Область определения гомоморфизма можно расширить до * следующим образом: h′(ax) = h(a)h′(x), h′( ) = . Здесь a , x *. Далее используется одно и тоже обозначение h для гомоморфизма на и *. 6

Часть 2: Гомоморфизм h определяет трансляцию (h) = {(x, h(x)) x *}. Устройство, которое по заданной цепочке x * находит соответствующую цепочку y = h(x), такую, что (x, y) (h), тривиально: оно должно посимвольно просмотреть входную цепочку x и заменить каждый её символ a на h(a). Это устройство является примером простейшего транслятора, реализующего трансляцию (h). 7

Часть 2: Трансляции и трансляторы Реалистичным примером транслятора, основанного на гомоморфизме, является простейший ассемблер. Транслятором для данной трансляции называется такое устройство, которое по данной входной строке x вычисляет выходную цепочку y, такую, что (x, y) . 8

Часть 2: Трансляции и трансляторы Желательными свойствами транслятора являются: 1) эффективность (время, затрачиваемое на перевод входной строки, должно быть линейно пропорционально её длине); 2) малый размер; 3) правильность (желательно иметь небольшой тест, такой, чтобы если транслятор прошёл его, то это гарантировало бы правильную работу транслятора на всех входных цепочках). 9

§ 1. 2. Схемы синтаксически управляемой трансляции Трансляторы являются средством реализации трансляций, хотя их можно рассматривать также и как способ задания трансляций. Способом спецификации трансляций, более сложных, чем те, которые описываются при помощи гомоморфизма, является аппарат схем синтаксически управляемых трансляций (sdts — syntaxdirected translation schema). 10

Часть 2: Схемы синтаксически управляемой трансляции Определение 1. 2. Схемой синтаксически управляемой трансляции называется формальная система T = (N, , , R, S), где N — алфавит нетерминалов; — конечный входной алфавит; — конечный выходной алфавит, причём N = и N = ; R — конечное множество правил схемы вида 11

Часть 2: Схемы синтаксически управляемой трансляции A , , где A N, (N )*, причём каждое вхождение нетерминала в цепочку взаимно однозначно связано с некоторым вхождением одноимённого нетерминала в , и эта связь является неотъемлемой частью правила; S N — начальный нетерминал. Цепочка называется синтаксической, а цепочка — семантической. 12

Часть 2: Схемы синтаксически управляемой трансляции Для указания связей между вхождениями нетерминалов можно использовать индексы. Например, связанные вхождения одноимённых нетерминалов помечаются одинаковыми индексами: A a. B(1)b. CB(2), B(2)B(1)d. C. 13

Часть 2: Трансляционные формы Определение 1. 3. Введем понятие трансляционной формы следующим образом: 1) (S, S) — начальная трансляционная форма, причём эти два вхождения начального нетерминала связаны друг с другом по определению; 14

Часть 2: Трансляционные формы 2) если ( A , ’A ’) — трансляционная форма, в которой два явно выделенных вхождения нетерминала A связаны, и если A , ’ — правило из R, то ( , ’ ’ ’) — трансляционная форма; причём связь между нетерминалами в и ’ такая же, как в правиле; нетерминалы в цепочках и связываются с нетерминалами в цепочках ’ и ’ в новой трансляционной форме точно так же, как в предыдущей; связь между нетерминалами является существенной чертой трансляционной формы; 15

Часть 2: Трансляционные формы 3) трансляционными формами являются такие и только такие пары цепочек, которые могут быть получены с помощью этих двух способов. Это определение фактически вводит отношение непосредственной выводимости одной трансляционной формы из другой. В таком случае принято писать: ( A , ′A ′) ( , ′ ′ ′). 16

Часть 2: Схемы синтаксически управляемой трансляции Для степени, транзитивного и рефлексивнотранзитивного замыкания этого отношения используются соответственно следующие обозначения: , и. Когда ясно, в какой схеме производится вывод, имя схемы может быть опущено. 17

Часть 2: Схемы синтаксически управляемой трансляции Определение 1. 4. Трансляция, заданная при помощи схемы синтаксически управляемой трансляции T, есть множество (T) = {(x, y) (S, S) (x, y), x *, y *} и называется синтаксически управляемой трансляцией (sdt syntax-directed translation). 18

Часть 2: Схемы синтаксически управляемой трансляции Определение 1. 5. Грамматика Gi = (N, , Pi, S), где Pi = {A A , R}, называется входной грамматикой схемы. Грамматика Go = (N, , Po, S), где Po = {A A , R}, называется выходной грамматикой схемы. Очевидно, что Gi и Go — контекстносвободные грамматики, порождающие входной и выходной языки трансляции, задаваемой схемой. 19

Ret 24 Пример 1. 2. Пусть sdts T = ({E, T, F}, {a, +, *, (, )}, {a, +, *}, R, E), где R = {(1) E E + T, E T +; (2) E T, T; (3) T T * F, T F *; (4) T F, F; (5) F (E), E; (6) F a, a }. Связь между нетерминалами в этих правилах очевидна, так как в синтаксической и семантической цепочках каждого правила не более чем одно вхождение нетерминала, представленного данным символом из {E, T, F}. 20

Часть 2: Пример 1. 2. Рассмотрим какой-нибудь левосторонний вывод в схеме T, например: (E, E) (E + T, ET+) (T(1) + T, T(1)T +) (F + T, FT +) (a + T, a. T+) (a + T * F, a. TF * +) (a + a*F, aa. F * +) (a + a*a, aaa * +). 21

Часть 2: Пример 1. 2. Нетрудно догадаться, что (T) = {(x, y) x — инфиксная запись, y — эквивалентная постфиксная запись арифметического выражения}. 22

Простые синтаксически управляемые трансляции Определение 1. 6. Схема синтаксически управляемой трансляции называется простой, если в каждом её правиле A , связанные нетерминалы в цепочках и встречаются в одинаковом порядке. Трансляция, определяемая простой схемой, называется простой синтаксически управляемой трансляцией. 23

Простые синтаксически управляемые трансляции Многие, но не все, полезные трансляции могут быть описаны как простые. В примере 1. 2 схема T, как и определяемая ею трансляция (T), является простой. Простые синтаксически управляемые трансляции интересны тем, что каждая из них может быть реализована транслятором в классе недетерминированных магазинных преобразователей (рис. 1. 1). 24

Простые синтаксически управляемые трансляции Другими словами, магазинные преобразователи характеризуют класс простых синтаксически управляемых трансляций таким же образом, как магазинные автоматы характеризуют класс контекстно-свободных языков. К рассмотрению таких трансляций мы сейчас и перейдем. 25

§ 1. 3. Магазинные преобразователи и синтаксически управляемые трансляции Здесь мы рассмотрим магазинные преобразователи, отличающиеся от магазинных автоматов тем, что у них есть выходная лента. 26

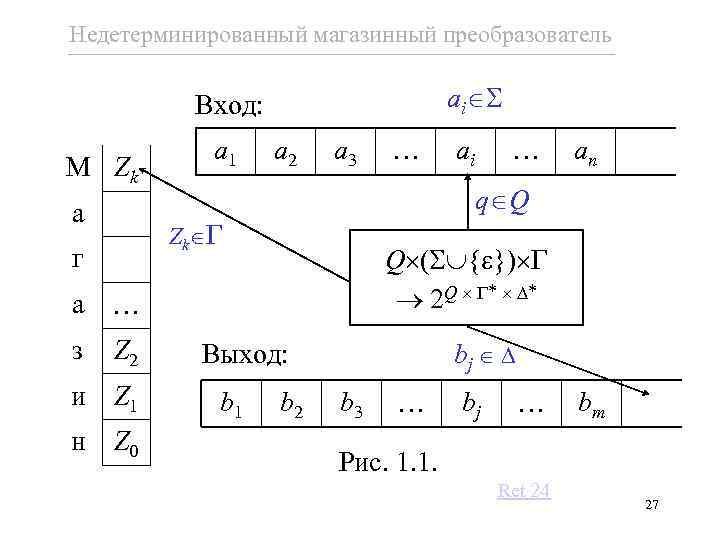Недетерминированный магазинный преобразователь ai Вход: М Zk а a 1 a 2 a 3 Z 2 и Z 1 н Z 0 an Q ( ) 2 Q а з ai q Q Zk г bj Выход: b 1 b 2 b 3 bj bm Рис. 1. 1. Ret 24 27

Определение 1. 7. Недерминированный магазинный преобразователь (npdt — nondeterministic pushdown transducer) есть формальная система P = (Q, , , q 0, Z 0, F), где Q — конечное множество состояний, — конечный входной алфавит, — конечный алфавит магазинных символов, — конечный выходной алфавит, q 0 Q — начальное состояние, Z 0 — начальный символ магазина, F Q — множество конечных состояний, — отображение типа Q ( { }) 2 Q * *, причём область значений представлена конечными подмножествами троек из Q * *. 28

Магазинный преобразователь Запись (q, a, Z) = означает, что npdt P, находясь в состоянии q Q, сканируя a на входной ленте или не зависимо от текущего входного символа в случае a = , имея Z на вершине магазина, переходит в одно из состояний pi Q, заменяя в магазине символ Z на цепочку i * и записывая цепочку yi * на выходную ленту. 29

Магазинный преобразователь При этом входная головка сдвигается на одну ячейку вправо, если a , иначе головка остается на месте, головка магазина сканирует последнюю запись в магазине, а головка выходной ленты размещается справа от последней её записи. 30

Магазинный преобразователь В частности: • если a = , то выбор действия не зависит от текущего входного символа и, как уже отмечалось, входная головка неподвижна; • если i = , то верхний символ магазина стирается, а вершина магазина опускается; • если yi = , то на выходную ленту ничего не пишется, и её головка остается на прежнем месте. 31

Магазинный преобразователь В начальный момент q = q 0, в магазине находится единственный символ Z 0, входная головка сканирует первую ячейку на входной ленте, а выходная лента пуста, причём её головка находится на первой ячейке. Работу магазинного преобразователя опишем в терминах конфигураций. 32

Магазинный преобразователь Определение 1. 8. Конфигурацией магазинного преобразователя P назовем четверку (q, x, , y), где q Q — текущее состояние, x * — часть входной цепочки от текущего символа до её последнего символа, называемая непросмотренной частью входной цепочки, * — содержимое магазина (будем считать, что первый символ цепочки есть верхний символ магазина), y * — вся выходная цепочка. 33

Магазинный преобразователь Таким образом, начальная конфигурация есть (q 0, x, Z 0, ), где x обозначает всю входную цепочку. Пусть (q, ax, Z , y) — текущая конфигурация, и (p, , z) (q, a, Z). Тогда один такт работы pdt P записывается как отношение между двумя последовательными конфигурациями: (q, ax, Z , y) (p, x, , yz). Здесь q Q, a { }, x *, Z , , *, y, z *. 34

Трансляция, реализуемая магазинным преобразователем Как обычно, определяются степень ( ), транзитивное замыкание ( ) и рефлексивнотранзитивное замыкание ( ) этого отношения. 35

Трансляция, реализуемая магазинным преобразователем Определение 1. 9. Говорят, что y * есть выход для x * при конечном состоянии, если (q 0, x, Z 0, ) (q, , , y) для некоторых q F и *. Трансляция, определяемая магазинным преобразователем P при конечном состоянии, есть (P) = {(x, y) (q 0, x, Z 0, ) (q, , , y) для некоторых q F и *}. 36

Трансляция, реализуемая магазинным преобразователем Говорят, что y * есть выход для x * при пустом магазине, если (q 0, x, Z 0, ) (q, , , y) для некоторого q Q. Трансляция, определяемая магазинным преобразователем P при пустом магазине, есть e(P) = {(x, y) (q 0, x, Z 0, ) (q, , , y) для некоторого q Q}. 37

Пример 1. 3. Пусть pdt P = ({q}, {a, +, *}, {E, +, *}, {a, +, *}, , q, E, {q}), где 1) (q, a, E) = {( q, , a)}, Входной символ 2) (q, +, E) = {( q, EE+, )}, используется 3) (q, *, E) = {( q, EE*, )}, 4) (q, , +) = {( q, , +)}, Входной символ не используется 5) (q, , *) = {( q, , *)}. Ret 66 38

Пример 1. 3. Рассмотрим действия pdt P на входе +*aaa: (q, +*aaa, E, ) (q, *aaa, EE+, ) (q, aaa, EE*E+, ) (q, aa, E*E+, a) (q, a, *E+, aa) (q, a, E+, aa*) (q, , +, aa*a) (q, , , aa*a+). Очевидно, что он преобразует префиксные арифметические выражения в постфиксные. Данный магазинный преобразователь является примером детерминированного магазинного преобразователя (см. определение 1. 10 далее). 39

Детерминированный магазинный преобразователь Определение 1. 10. Магазинный преобразователь P = (Q, , , q 0, Z 0, F) называется детерминированным (dpdt), если 1) # (q, a, Z) 1 для всех q Q, a { } и Z ; 2) если (q, , Z) для данных q Q и Z , то (q, a, Z) = для всех a . 40

Детерминированный магазинный преобразователь На практике предпочитают использовать детерминированными магазинными преобразователями (dpdt), поскольку в реализации они оказываются более эффективными по сравнению с недетерминированными магазинными преобразователями (npdt). Когда неважно различать, о каких преобразователях, детерминированных или недетерминированных, идёт речь, используется обозначение pdt. 41

Лемма 1. 1. Пусть T = (N, , , R, S) — простая схема синтаксически управляемой трансляции. Существует недетерминированный магазинный преобразователь P, такой, что e(P) = (T). Доказательство. Построим npdt P, о котором идёт речь, и покажем, что он реализует трансляцию (T). Ret 65 42

(T) e(P) Положим P = ({q}, , N ’, , , q, S, ). Чтобы отличать в магазине P входные символы от выходных, последние переименовываются с помощью гомоморфизма h, определяемого для каждого выходного символа b при помощи равенства h(b) = b’ таким образом, чтобы множество символов ’ = {b’ b } не пересекалось со словарем , т. е. ’ = . 43

(T) e(P) Отображение определяется так: 1. (q, x 0 y 0’B 1 x 1 y 1’…Bmxmym’, ) (q, , A), если A x 0 B 1 x 1 … Bmxm, y 0 B 1 y 1… Bmym R, yi’ = h(yi), i = 1, 2, …, m, где m 0. Здесь h(by) = b'h(y) для каждого b и y *, h( ) = . 2. (q, a, a) = {(q, , )} для всех a . 3. (q, , b') = {(q, , b)} для всех b . Ret 53 Ret 55 44

(T) e(P) I. Докажем сначала, что если (S, S) (x, y), то (q, x, S, ) (q, , , y). Для этого индукцией по длине вывода l докажем более общее утверждение для любого A N: если существует вывод (A, A) (x, y), то (q, x, A, ) (q, , , y). База. Пусть l = 1. Имеем (A, A) (x, y). На этом единственном шаге вывода применяется правило A x, y R. Ret 52 45

(T) e(P) Согласно п. 1 определения имеем (q, xy’, ) (q, , A). Поэтому (q, x, A, ) (q, x, xy’, ). Далее согласно п. 2 (q, x, xy’, ) (q, , y’, ). Наконец, согласно п. 3 имеем (q, , y’, ) (q, , , y). Итак, существует переход (q, x, A, ) (q, , , y). 46

(T) e(P) Индукционная гипотеза. Предположим, что вспомогательное утверждение выполняется для всех выводов длиной l n (n 1). Индукционный переход. Докажем утверждение для l = n + 1. Пусть (A, A) (x 0 B 1 x 1… Bmxm, y 0 B 1 y 1…Bmym) (x, y) — вывод длиной n + 1. Очевидно, что x = x 0 t 1 x 1 t 2 x 2…tmxm, y = y 0 z 1 y 1 z 2 y 2…zmym , (1. 1) и (Bi, Bi) (ti, zi), li n, i = 1, 2, …, m. (1. 2) 47

(T) e(P) На первом шаге данного вывода было применено правило A x 0 B 1 x 1 B 2 x 2…Bmxm, y 0 B 1 y 1 B 2 y 2…Bmym R и потому согласно п. 1 построения имеем (q, x 0 y 0’B 1 x 1 y 1’B 2 x 2 y 2’… Bmxmym’B, ) (q, , A). (1. 3) Кроме того, согласно индукционной гипотезе из существования частичных выводов (1. 2), следует возможность перехода (q, ti, Bi, ) (q, , , zi), i = 1, 2, …, m. (1. 4) 48

(T) e(P) Рассмотрим движения pdt P. Учитывая условия (1. 1) и (1. 3), имеем (q, x, A, ) = (q, x 0 t 1 x 1 t 2 x 2…tmxm, A, ) (q, x 0 t 1 x 1 t 2 x 2…tmxm, x 0 y 0’B 1 x 1 y 1’B 2 x 2 y 2’…Bmxmym’, ). Согласно п. 2 построений имеем переход (q, x 0 t 1 x 1 t 2 x 2…tmxm, x 0 y 0’B 1 x 1 y 1’B 2 x 2 y 2’…Bmxmym’, ) (q, t 1 x 1 t 2 x 2…tmxm, y 0’B 1 x 1 y 1’B 2 x 2 y 2’…Bmxmym’, ); согласно п. 3 построений имеем переход (q, t 1 x 1 t 2 x 2…tmxm, y 0’B 1 x 1 y 1’B 2 x 2 y 2’…Bmxmym’, ) (q, t 1 x 1…tmxm, B 1 x 1 y 1’B 2 x 2 y 2’…Bmxmym’, y 0). 49

(T) e(P) Учитывая существование перехода (1. 4) для i = 1, получаем: (q, t 1 x 1 t 2 x 2…tmxm, B 1 x 1 y 1’B 2 x 2 y 2’ … Bmxmym’, y 0) (q, x 1 t 2 x 2…tmxm, x 1 y 1’B 2 x 2 y 2’…Bmxmym’, y 0 z 1). Далее рассуждения с использованием пп. 2, 3 построений, а также переходов (1. 4) для i = 2, 3, …, m, повторяются. В результате получаем последующие движения: 50

(T) e(P) (q, x 1 t 2 x 2…tmxm, x 1 y 1’B 2 x 2 y 2’ … Bmxmym’, y 0 z 1) (q, t 2 x 2…tmxm, y 1’B 2 x 2 y 2’… Bmxmym’, y 0 z 1) (q, t 2 x 2…tmxm, B 2 x 2 y 2’… Bmxmym’, y 0 z 1 y 1) … (q, tmxm, Bmxmym’, y 0 z 1 y 1… zm– 1 ym– 1) (q, xmym’, y 0 z 1 y 1… zm– 1 ym– 1 zm) (q, , , y 0 z 1 y 1… zm– 1 ym– 1 zmym) = (q, , , y). 51

(T) e(P) В конце рассуждений о движениях pdt P принято во внимание представление цепочки y согласно равенству (1. 1). Итак, вся последовательность движений может быть представлена в виде (q, x, A, ) (q, , , y). В частности, из доказанного вспомогательного утверждения при A = S следует утверждение I. 52

e(P) (T) II. Докажем теперь обратное утверждение: если (q, x, S, ) (q, , , y) , то (S, S) (x, y). Для этого индукцией по числу l движений типа 1, независимых от входных символов, определённых согласно п. 1 построений, докажем более общее утверждение для любого A N : если (q, x, A, ) (q, , , y), то (A, A) (x, y). 53

e(P) (T) База. Пусть l = 1. Имеем (q, x, A, ) (q, , , y), где только одно движение типа 1. Очевидно, что оно — первое движение, так как в исходной конфигурации на вершине магазина находится A N. Это движение не может привести к появлению нетерминалов в магазинной цепочке из-за того, что они неизбежно привели бы к другим движениям типа 1. 54

e(P) (T) Кроме того, магазинная цепочка, замещающая A на вершине магазина, должна начинаться на x, так как только в этом случае удаcться продвинуться по входу x (за счёт движений, определённых в п. 2, которые используют входные символы). Наконец, магазинная цепочка должна заканчиваться на y’, потому что только в этом случае на выходе может образоваться цепочка y (за счёт движений, определённых в п. 3 , которые переносят образы выходных символов из магазина на выход). 55

e(P) (T) Поэтому фактически имеем (q, x, A, ) (q, x, xy’, ) (q, , , y), где первое движение обусловлено тем, что (q, xy’, ) (q, , A), а это означает существование правила A x, y R. Два последних перехода выполнены согласно пп. 2, 3 построений. Воспользовавшись существующим правилом, немедленно получаем вывод (A, A) (x, y). 56

e(P) (T) Индукционная гипотеза. Предположим, что вспомогательное утверждение выполняется для всех l n (n 1). Индукционный переход. Докажем утверждение для l = n + 1. Пусть имеется переход (q, x, A, ) (q, , , y), в котором ровно n + 1 движение типа 1. 57

e(P) (T) Поскольку в исходной конфигурации на вершине магазина A N, то первое же движение — типа 1: (q, x, A, ) (q, x, x 0 y 0’B 1 x 1 y 1’…Bmxmym’, ) (q, , , y). (1. 5) В конечной конфигурации магазин пуст. Цепочка x 0 *, появившаяся в верхней части магазина после первого движения, может быть удалена только, если входная цепочка x начинается на x 0. Ret 63 58

e(P) (T) Поэтому далее последуют движения, определяемые п. 2, которые продвинут вход по x 0 и удалят такую же цепочку из магазина. (q, x, A, ) (q, x 0 y 0’B 1 x 1 y 1’…Bmxmym’, ) (q, , y 0’B 1 x 1 y 1’…Bmxmym’, )… Далее ряд движений, определяемых п. 3, удалит цепочку y 0’ из магазина, выдав на выход y 0, и символ B 1 окажется на вершине магазина. (q, , B 1 x 1 y 1’…Bmxmym’, y 0) = 59

e(P) (T) К моменту, когда вершина магазина опустится ниже позиции B 1, будет просканирована некоторая часть входа t 1, следующая за цепочкой x 0, т. е. а на выходе образуется некоторая цепочка z 1: = (q, , B 1 x 1 y 1’…Bm xm ym’, y 0) (q, , x 1 y 1’…Bm xm ym’, y 0 z 1) 60

e(P) (T) Далее мы можем повторить рассуждения, аналогичные предыдущим, относя их к цепочкам xi *, yi’ ’ (i = 1, 2, …, m) и Bj N ( j = 2, …, m), последовательно появляющимся в верхней части магазина в результате серии движений, построенных в соответствии с п. 2, затем п. 3, и ряда движений, приводящих к понижению вершины магазина ниже позиции, занимаемой Bj. 61

e(P) (T) Другими словами, детальный разбор возможных движений от исходной конфигурации к конечной даёт основание утверждать, что вход x и выход y представимы в виде x = x 0 t 1 x 1…tmxm, y = y 0 z 1 y 1…zmym, (1. 6) причём (q, ti, Bi, ) (q, , , zi), (1. 7) li n, i = 1, 2, …, m. 62

e(P) (T) По построению первое движение (1. 5) обусловлено существованием правила A x 0 B 1 x 1… Bmxm, y 0 B 1 y 1…Bmym R, (1. 8) а из существования движений (1. 7) по индукционному предположению следует существование выводов (Bi, Bi) (ti , zi), i = 1, 2, …, m. (1. 9) Используя (1. 8) и (1. 9), с учетом (1. 6) получаем: (A, A) (x 0 B 1 x 1…Bmxm, y 0 B 1 y 1…Bmym) (x 0 t 1 x 1…tmxm, y 0 z 1 y 1…zmym) = (x, y). 63

e(P) (T) В частности, при A = S следует утверждение II. Из рассуждений I и II следует утверждение леммы. Доказанная лемма даёт алгоритм построения недетерминированного магазинного преобразователя, эквивалентного данной простой схеме синтаксически управляемой трансляции. 64

Пример 1. 4. Пусть sdts T = ({E}, {a, +, *}, R, E), где R = {(1) E +EE, EE+ ; (2) E *EE, EE* ; (3) E a, a}. По лемме 1. 1 эквивалентный npdt есть P = ({q}, {a, +, *}, {E, a, +, *, a’, +’, *’}, {a, +, *}, , q, E, ), где 1) (q, , E) = { (q, +EE+’, ), (q, *EE*’, ), (q, aa’, )}, 2) (q, b, b) = {( q, , )} для всех b {a, +, *}, 3) (q, , с’) = {( q, , с)} для всех с {a, +, *}. 65

Пример 1. 4. Сравните этот недетерминированный магазинный преобразователь с эквивалентным детерминированным преобразователем из примера 1. 3. Оба преобразуют префиксные арифметические выражения в постфиксные. (q, +*aaa, E, ) (q, +*aaa, +EE+’, ) (q, *aaa, EE+’, ) (q, aaa, EE*’E+’, ) (q, *aaa, *EE*’E+’, ) (q, aaa, aa’E*’E+’, ) (q, aa, E*’E+’, a) (q, aa’ *’E+’, a) (q, a, aa’+’, aa*) (q, , , a a * a +). (q, a, *’E+’, aa) (q, , a’+’, aa*) (q, a, E+’, a a *) (q, , +’, a a * a) 66

e(P) (T) Лемма 1. 2. Пусть P = (Q, , , q 0, Z 0, ) — недетерминированный магазинный преобразователь. Существует простая схема синтаксически-управляемой трансляции T, такая, что (T) = e(P). Доказательство. Построим такую схему T следующим образом (ср. с теор. 5. 3). Положим T = (N, , , R, S), где N = {S} {[q. Zp] q, p Q, Z }, и — такие же, как в npdt P, Ret 82 67

e(P) (T) R = {S [q 0 Z 0 p], [q 0 Z 0 p] для всех p Q} {[q. Zp] a[q 1 Z 1 q 2][q 2 Z 2 q 3]…[qm. Zmqm+1], y[q 1 Z 1 q 2][q 2 Z 2 q 3]…[qm. Zmqm+1] (q 1, Z 1 Z 2…Zm, y) (q, a, Z); a { }, y *; p, q, qi Q; Z, Zi ; i = 1, 2, …, m; qm+1= p}. I. Докажем сначала, что если (q, x, Z, ) (p, , , y), то ([q. Zp], [q. Zp]) (x, y), используя индукцию по числу l движений ndpt P. 68

e(P) (T) База. Пусть l = 1. Имеем (q, x, Z, ) (p, , , y). В этом случае x { } и (p, , y) (q, x, Z). Тогда по построению схемы T существует правило [q. Zp] x, y R, с помощью которого немедленно получаем: ([q. Zp], [q. Zp]) (x, y). 69

e(P) (T) Индукционная гипотеза. Предположим, что утверждение I выполняется для всех переходов между конфигурациями за число движений l n (n 1). Индукционный переход. Докажем, что тогда утверждение I справедливо и для l = n + 1. Итак, пусть (q, x, Z, ) (p, , , y). Рассмотрим этот переход подробнее. 70

e(P) (T) В общем случае первое движение имеет вид (q, x, Z, ) = (q, ax’, Z, ) (q 1, x’, Z 1 Z 2…Zm, y 0). (1. 10) Затем следуют дальнейшие движения: (q 1, x’, Z 1 Z 2…Zm, y 0) = = (q 1, x 1 x 2…xm, Z 1 Z 2…Zm, y 0) (q 2, x 2…xm, Z 2…Zm, y 0 y 1) … (qm+1, , , y 0 y 1 y 2…ym) = (p, , , y). (1. 11) Здесь a { }, x = ax 1 x 2 … xm, y = y 0 y 1 y 2…ym, 71

e(P) (T) причём (qi, xi, Zi, ) (qi + 1, , , yi), (1. 12) i = 1, 2, …, m; li n; qm+1 = p. Первое движение (1. 10) существует потому, что (q 1, Z 1 Z 2…Zm, y 0) (q, a, Z), следовательно, по способу построения правил схемы в ней имеется правило [q. Zp] a[q 1 Z 1 q 2][q 2 Z 2 q 3]…[qm. Zmqm+1], y 0[q 1 Z 1 q 2][q 2 Z 2 q 3]…[qm. Zmqm+1], (1. 13) в обозначениях нетерминалов которого участвуют те состояния, по которым проходил npdt P. 72

e(P) (T) Из последующих движений (1. 11) согласно индукционной гипотезе, применённой к (1. 12), следует существование выводов ([qi. Ziqi+1], [qi. Ziqi+1]) (xi, yi), (1. 14) i = 1, 2, …, m. Из (1. 13) и (1. 14) можно выстроить требуемый вывод: ([q. Zp], [q. Zp]) (a[q 1 Z 1 q 2]…[qm. Zmqm+1], y 0[q 1 Z 1 q 2]…[qm. Zmqm+1]) (ax 1 x 2…xm, y 0 y 1…ym) = (x, y). 73

e(P) (T) II. Индукцией по длине l вывода докажем теперь обратное утверждение: если ([q. Zp], [q. Zp]) (x, y), то (q, x, Z, ) (p, , , y). База. Пусть l = 1. Имеем ([q. Zp], [q. Zp]) (x, y). На единственном шаге этого вывода использовано правило схемы [q. Zp] x, y, которое обязано своим происхождением тому, что (p, , y) (q, x, Z), где x { }, y *, а тогда (q, x, Z, ) (p, , , y). 74

e(P) (T) Индукционная гипотеза. Предположим, что аналогичное утверждение выполняется для всех выводов, длина которых не превосходит n (n 1). Индукционный переход. Докажем аналогичное утверждение для выводов длиной l = n + 1. Пусть ([q. Zp], [q. Zp]) (a[q 1 Z 1 q 2]…[qm. Zmqm+1], y 0[q 1 Z 1 q 2]…[qm. Zmqm+1]) (x, y). (1. 15) 75

e(P) (T) Из (1. 15) следует, что существует правило [q. Zp] a[q 1 Z 1 q 2]…[qm. Zmqm+1], y[q 1 Z 1 q 2]…[qm. Zmqm+1] R, которое обязано своим происхождение тому, что (q 1, Z 1…Zm, y) (q, a, Z). (1. 16) 76

e(P) (T) Кроме того, из (1. 15) следует, что x = ax 1…xm, y = y 0 y 1…ym, (1. 17) ([qi. Ziqi +1], [qi. Ziqi +1]) (xi, yi), li n, а тогда согласно индукционной гипотезе (qi, xi, Zi, ) (qi+1, , , yi), (1. 18) i = 1, 2, …, m; qm+1= p. Из (1. 16) и (1. 18) с учетом (1. 17) выстраивается последовательность движений: (q, x, Z, ) = (q, ax 1…xm, Z, ) (q 1, x 1…xm, Z 1…Zm, y 0) (p, , , y 0 y 1…ym) = (p, , , y). 77

e(P) (T) Из рассуждений I и II следует, что для любых q, p Q и Z вывод ([q. Zp], [q. Zp]) (x, y) существует тогда и только тогда, когда (q, x, Z, ) (p, , , y). В частности, это справедливо для q = q 0 и Z = Z 0. 78

e(P) (T) В то же время при помощи правила вида S [q 0 Z 0 p], [q 0 Z 0 p] всегда можно пристроить начало к вышеприведённому выводу, чтобы считать доказанным утверждение: (S, S) ([q 0 Z 0 p], [q 0 Z 0 p]) (x, y) тогда и только тогда, когда (q 0, x, Z 0, ) (p, , , y). Лемма доказана. 79

e(P) (T) Из лемм 1. 1 и 1. 2 следует Теорема 1. 1. Трансляция = (T), где T — простая схема синтаксически управляемой трансляции, существует тогда и только тогда, когда существует недетерминированный магазинный преобразователь P, такой, что e(P) = . Ret 106 80

Пример 1. 5. В предыдущем примере по простой sdts T = ({E}, {a, +, *}, R, E), где R = { (1) E +EE, EE+ ; (2) E *EE, EE* ; (3) E a, a}, был построен эквивалентный npdt P = ({q}, {a, +, *}, {E, a, +, *, a’, +’, *’}, {a, +, *}, , q, E, ), где 1) (q, , E) = {(q, +EE+’, ), (q, *EE*’, ), (q, aa’, )}, 2) (q, b, b) = {( q, , )} для всех b {a, +, *}, 3) (q, , с’) = {( q, , с)} для всех с {a, +, *}. Ret 84 81

Пример 1. 5. Теперь по этому недетерминированному преобразователю P мы построим эквивалентную простую схему синтаксически управляемой трансляции, воспользовавшись алгоритмом, описанным в лемме 1. 2. 82

Пример 1. 5. Положим T = ({S, [q. Eq], [qaq], [q+q], [q*q], [qa’q], [q+’q], [q*’q]}, {a, +, *}, R, S), R = {(1) S [q. Eq], [q. Eq]; (2) [q. Eq] [q+q] [q. Eq] [q+’q], [q+q] [q. Eq] [q+’q]; (3) [q. Eq] [q*q] [q. Eq] [q*’q], [q*q] [q. Eq] [q*’q]; (4) [q. Eq] [qaq] [qa’q], [qaq] [qa’q]; (5) [qaq] a, ; (8) [qa’q] , a; (6) [q+q] +, ; (9) [q+’q] , +; (7) [q*q] *, ; (10) [q*’q] , *}. 83

Пример 1. 5. Эта схема мало похожа на исходную, в которой было всего три правила. Однако её можно эквивалентными преобразованиями привести к исходной. 84

Пример 1. 5. Во-первых, правые части правил 5– 10 можно подставить в правые части правил 2– 4. В результате получим R’ = { (1) S [q. Eq], [q. Eq]; (2’) [q. Eq] +[q. Eq], [q. Eq]+; (3’) [q. Eq] *[q. Eq], [q. Eq]*; (4’) [q. Eq] a, a}. Легко видеть, что из (S, S) выводится в точности то же, что и из ([q. Eq], [q. Eq]). Остается заменить в правилах 2’– 4’ слева и справа [q. Eq] на простое E и отбросить бесполезное правило 1, чтобы получить исходную схему. 85