Теория Электрической Связи Часть 1 Сокращенный вариант курса

Теория Электрической Связи (Часть 1) Сокращенный вариант курса прочитанный доц. Филипповым Б. И. в Сиб. ГУТИ

Задачи курса: 1. Математическое описание сигналов. 2. Преобразование случайных сигналов в линейных и нелинейных цепях. 3. Различные модуляции аналоговых сигналов. 4. Теория информации. 5. Теория помехоустойчивости. 6. Вопросы организации многоканальной электросвязи.

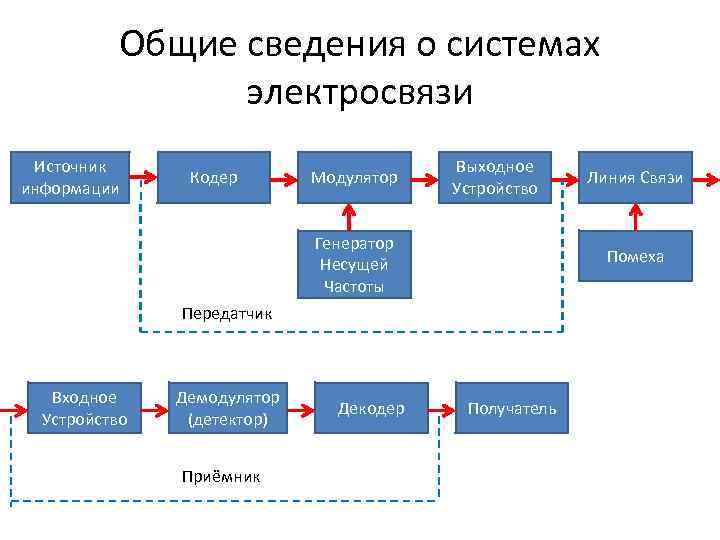Общие сведения о системах электросвязи Источник информации Кодер Модулятор Выходное Устройство Генератор Несущей Частоты Помеха Передатчик Входное Устройство Демодулятор (детектор) Приёмник Декодер Линия Связи Получатель

1. Источник информации – человек, ЭВМ. 2. Кодер. Функции кодера: а) Преобразование кодовых комбинаций. б) Дискретизация по времени. в) Дискретизация по амплитуде (квантование). г) Убирает лишнее из информации (уменьшает избыточность). д) Вводит избыточность (помехоустойчивое кодирование). 3. Модулятор. Переносит низкочастотный спектр в область высоких частот. 4. Генератор несущей частоты – генератор синусоидальных колебаний. 5. Выходное устройство. Задача – довести сигнал до необходимого уровня. 6. Линия связи. Например: Кабель, свободное пространство.

7. Помеха. Это любое случайное воздействие, препятствующее правильному приёму сигнала. 8. Входное устройство. Выделяет из всех сигналов нужный. Имеет избирательный контур. 9. Демодуляция – процесс обратный модуляции. Понижает спектр до низких частот. 10. Декодер. Выполняет операцию обратную кодированию. Переводит сигнал в удобную для потребителя форму. Модулятор + Демодулятор = Модем Кодер + Декодер = Кодек Кодер + Модулятор + Демодулятор + Декодер = Кодем

Сигналы Связи. Сигнал – физическое колебание, осуществляющее передачу информацию из одной точки в другую. Электрический сигнал –сигнал, который использует электрическое возмущение. Классификация Сигналов. I. С информационной точки зрения. Делятся на детерминированные и случайные. Детерминированный сигнал – его значение можно предсказать в любой момент времени с вероятностью равной 1. Описываются детерминированными функциями времени. Полностью детерминированных сигналов в природе нет. Случайный сигнал – значение случайного сигнала в любой момент времени предсказывается с вероятностью меньше 1.

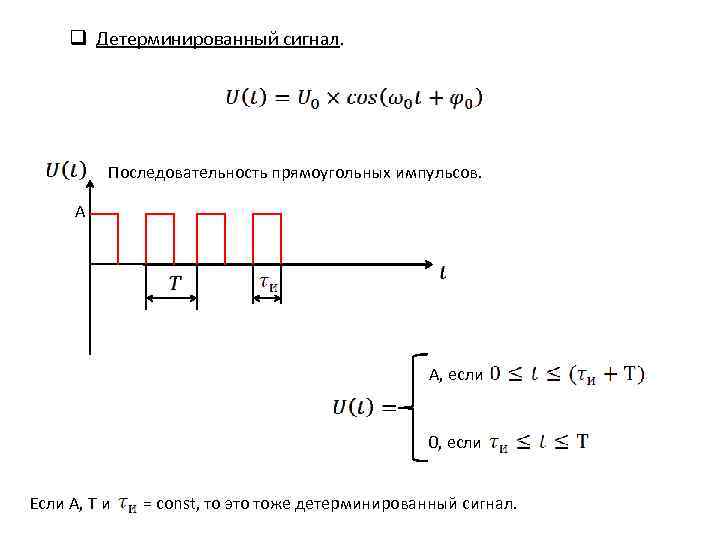q Детерминированный сигнал. Последовательность прямоугольных импульсов. А А, если 0, если Если А, Т и = const, то это тоже детерминированный сигнал.

q Случайный сигнал. ξ (t) ξ ξ Информационные сигналы – случайные. Это означает что мы заранее не знаем, что будет на приёме.

II. По виду временной функции. a) b) c) d) Непрерывные. Дискретные. Цифровые. Импульсные. дискретное непрерывное : дискретное непрерывное

Непрерывный и по времени и по амплитуде Дискретный по амплитуде, непрерывный по времени Непрерывный по амплитуде, дискретный по времени Дискретный и по времени и по амплитуде

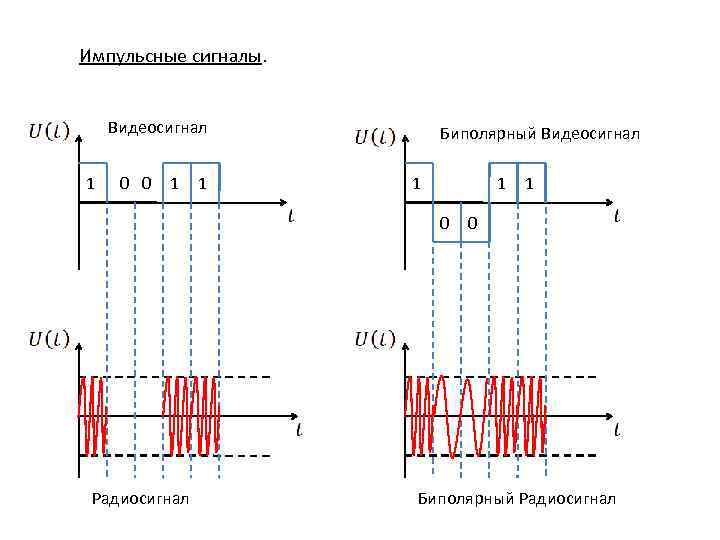Импульсные сигналы. Видеосигнал 1 0 0 1 1 Биполярный Видеосигнал 1 1 0 Радиосигнал 1 0 Биполярный Радиосигнал

III. По физическим характеристикам. Нужно знать физические характеристики сигнала для того, чтобы передавать его по каналу связи. Сигнал и канал должны быть согласованы. Сигнал связи Канал связи Сигнал характеризуется следующими параметрами: 1. - время существования сигнала. 2. - полоса частот, занимаемая сигналом. 3. - динамический диапазон.

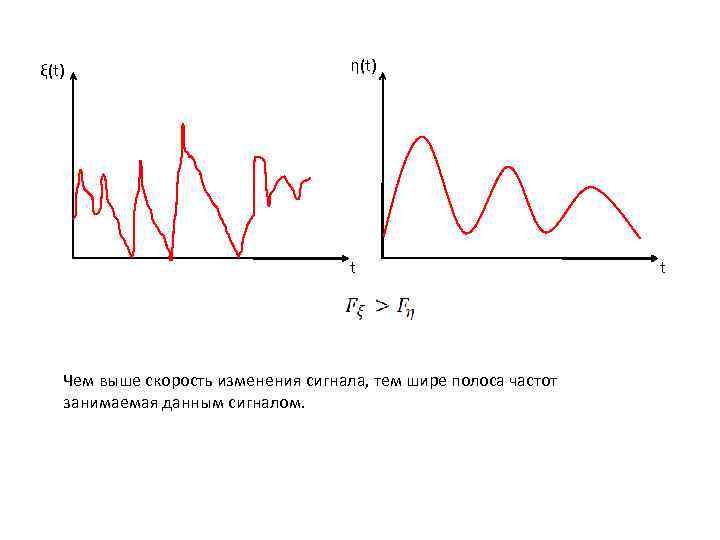ξ(t) η(t) t Чем выше скорость изменения сигнала, тем шире полоса частот занимаемая данным сигналом. t

Полоса частот Реальный сигнал имеет бесконечный спектр. ( ) =90 -95 %; ( ) = 100% Объём сигнала: Объём канала: Условие согласования канала:

IV. По виду передаваемого сообщения. a) Телефонный. (Речь) b) Телеграфный. (Текст) c) Фототелеграфный. (Неподвижное изображение) d) Передача данных. e) Сигнал звукового вещания. f) Телевизионный. q Телефонный сигнал - формируется микрофоном. Задача телефонного канала – точность и разборчивость. = 50 = 25 10000 Гц, рекомендуемый канал МККТТ: 0, 3 35 д. Б 3, 4 к. Гц.

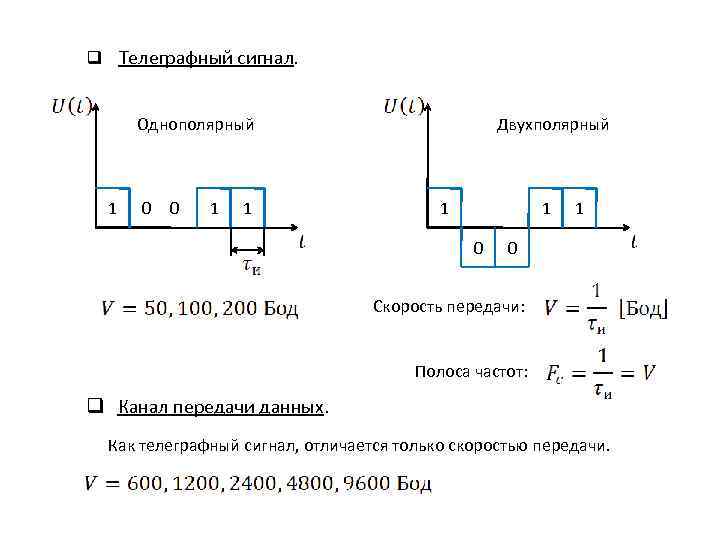q Телеграфный сигнал. Однополярный 1 0 0 1 1 Двухполярный 1 1 0 Скорость передачи: Полоса частот: q Канал передачи данных. Как телеграфный сигнал, отличается только скоростью передачи.

q Фототелеграфный канал. Используется для передачи неподвижных изображений. q Сигнал звукового вещания. - для симфонического оркестра. q Телевизионный сигнал.

Кодирование, Декодирование, Модуляция, Демодуляция Это основные преобразования происходящие в современных системах связи. q Кодирование – представление элементов дискретного сообщения в виде кодовых комбинаций, по определенному правилу. Пример : ТЛГ № 2 – сигнал использующийся для передачи текста. буквы (комбинации). n=5 (11001, 10110, 00001) В ЭВМ используется восьмеричный код. q Декодирование - операция обратная кодированию. Сигнал восстанавливается при декодировании кодовых комбинаций.

q Модуляция – преобразование первичного сигнала сообщения в другой сигнал, наиболее пригодный для передачи по каналу связи. - Амплитудная модуляция - Частотная модуляция - Фазовая модуляция - Высокие частоты (ВЧ); - Низкие частоты (НЧ) - Модулирующий сигнал q Демодуляция – процесс, обратный модуляции. Сигнал на выходе демодулятора должен быть равен сигналу на входе модулятора.

Детерминированные сигналы. Их классификация. Значения детерминированного сигнала известны в любой момент времени с вероятностью 1. Детерминированные сигналы информации не несут. Используются: Ø При всевозможных измерениях. Ø Отрезки этих сигналов используются при передачи. Классификация: 1) Периодические. 2) Непериодические. 3) Почти периодические.

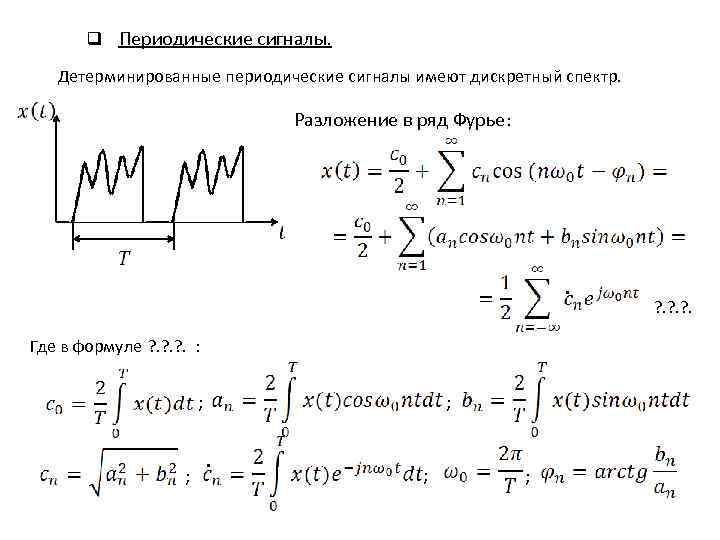q Периодические сигналы. Детерминированные периодические сигналы имеют дискретный спектр. Разложение в ряд Фурье: . Где в формуле ? . ? . : ; ; ; ? . ? .

q Непериодические сигналы. Детерминированные непериодические сигналы имеют сплошной спектр. Связь между временной и спектральной характеристикой определяется интегралом Фурье. Прямое преобразование Фурье : Обратное преобразование Фурье : q Почти периодические сигналы. Имеют большой период повторения. - Непрерывное время. - Дискретный спектр. Это модулированные сигналы.

Разложение сигналов в ряд по ортогональным функциям. Для исследования различных свойств сообщений (сигналов и помех) используются их разложения в ортогональные ряды (функции). Любой сигнал или помеху можно представить в виде ряда: ? . ? . - Ортогональные простейшие функции, неслучайные. Например: , если - Случайный коэффициент: - Энергия ортогональных функций.

Если , то ряд (1) – ряд Фурье. . .

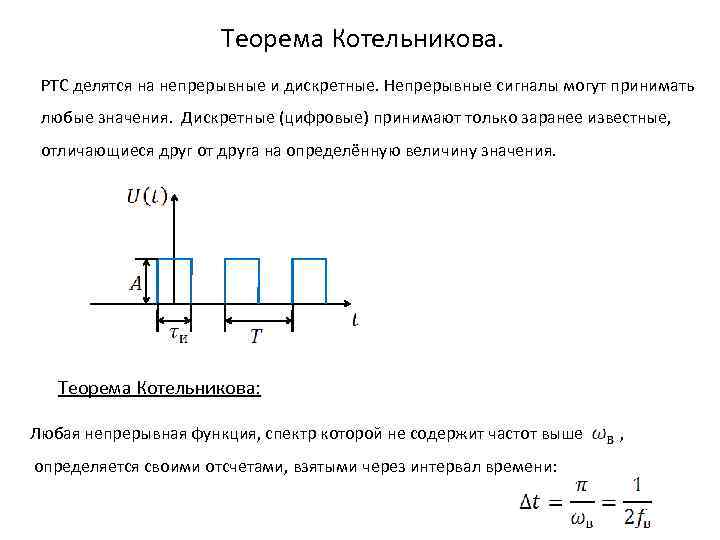Теорема Котельникова. РТС делятся на непрерывные и дискретные. Непрерывные сигналы могут принимать любые значения. Дискретные (цифровые) принимают только заранее известные, отличающиеся друг от друга на определённую величину значения. Теорема Котельникова: Любая непрерывная функция, спектр которой не содержит частот выше определяется своими отсчетами, взятыми через интервал времени: ,

- интервал Котельникова. - аппроксимирующая функция.

Доказательство теоремы Котельникова основывается на преобразовании Фурье. ; ; Далее вывод теоремы Котельникова основывается на разложении функции в комплексный ряд Фурье, и на осуществлении перехода от и , , от , . С математической точки зрения теорема Котельникова означает представление сигнала в виде ряда: ? . ? . Где в формуле ? . ? . - отсчёты, ( - наивысшая частота спектра сигнала. ), - функция отсчётов,

Ряд Котельникова – это разложение сигнала в ряд по ортогональным функциям. Вывод: Ряд Котельникова является основанием для восстановления на приёме непрерывного сигнала по отсчётам. Ряд Котельникова лежит в основе всех импульсных способов передачи сигналов: a) ИКМ – Импульсно – Кодовая Модуляция. b) АИМ – Амплитудно – Импульсная Модуляция. c) ШИМ – Широтно – Импульсная Модуляция. d) ФИМ – Фазо – Импульсная Модуляция. Замечание: 1. - нельзя, так как , иначе будет потеряна информация об исходном сообщении. 2. - можно, если , то .

Восстановление непрерывного сигнала по отсчётам. ? . ? . Импульсная характеристика ИФНЧ определяется как: ; ; ; Формула ? . ? . Определяет точки, где функция ; ? . ? . обращается в ноль. Спектр на выходе ИФНЧ: ? . ? . - Спектр дискретизированного сигнала. - Спектр входного воздействия. - Частота дискретизации. Вывод: Таким образом для восстановления исходного сигнала по отсчетам достаточно подать эти отсчёты на ИФНЧ и получим исходную функцию .

Погрешности дискретизации и восстановления непрерывного сигнала. 1. Теорема Котельникова справедлива только для финитных сигналов. 1 Финитный сигнал. ? . ? . 2 Реальный сигнал. ? . ? . Погрешность дискретизации

2. Нельзя получить ИФНЧ. Рассмотрим простейший ФНЧ (RC - цепочка). Реальный. Исходный (идеальный). Импульсная характеристика нашего ФНЧ: Вывод: Чем выше ? . ? . и чем ближе характеристика ФНЧ приближается к идеальной, тем точнее восстановление переданного сигнала.

Методы формирования и преобразования сигналов. Классификация радиотехнических цепей. Любая радиотехническая или электрическая цепь описывается дифференциальным уравнением ? . ? . ? . Исходя из этого уравнения, получим все виды цепей: 1. Линейные электрические цепи. 2. Нелинейные электрические цепи. 3. Параметрические электрические цепи.

1. Линейные электрические цепи (ЛЭЦ). Для ЛЭЦ справедлив принцип суперпозиции: реакция на суммарное воздействие равна сумме реакций на каждое из воздействий в отдельности. Пример: - Характеристика цепи. Тогда Пусть , а В ЛЭЦ невозможно появление новых частот, не содержащихся во входных сигналах.

2. Нелинейные электрические цепи (НЭЦ). Для НЭЦ неприменим принцип суперпозиции. Пример: ; ; В НЭЦ возникают новые частоты, не содержащихся во входных воздействиях, это положительный момент.

3. Параметрические электрические цепи (ПЭЦ). Для ПЭЦ: 1. Справедлив принцип суперпозиции. 2. Возникают новые частоты, не содержащиеся во входных воздействиях. ПЭЦ конструируются на основе НЭ, на которые подаются напряжения, зависимые от времени. Пример: ПЭЦ

Принципы преобразования сигналов. Воздействие НЭ ПЭ Отклик На входе Спектр воздействия: Функция плотности вероятностей: Функция распределения вероятностей: Математическое ожидание: Дисперсия: Функция корреляции: Интервал корреляции: Коэффициент корреляции: Энергетический спектр: Полоса спектра: На выходе

Преобразования бывают: 1. Пассивные – преобразование, при котором не возникает новых частот. 2. Активные – преобразование, при котором появление новых частот имеет большое значение в технике связи. Активное преобразование предполагает использование либо нелинейных элементов, либо параметрических элементов. При использовании нелинейных элементов мы используем аппроксимации НЭ: 1. Степенной полином. Метод тригонометрических функций. 2. Отрезками прямых линий. Метод угла отсечки.

Пример степенного полинома: - Характеристика НЭЦ - Возмущение воздействия Тогда получим: Так как Амплитуда 1 -й гармоники Постоянная составляющая Амплитуда 2 -й гармоники ? . ? .

Бигармоническое колебание для нелинейного элемента: Если , и Тогда, Кратные гармоники появляются за счёт квадратичного члена, а суммарно-разностные в результате умножения частот (перекрестные члены).

Бигармоническое колебание для параметрического элемента: Воздействие Отклик При преобразованиях, кроме НЭ, часто используются фильтры, то есть линейные элементы.

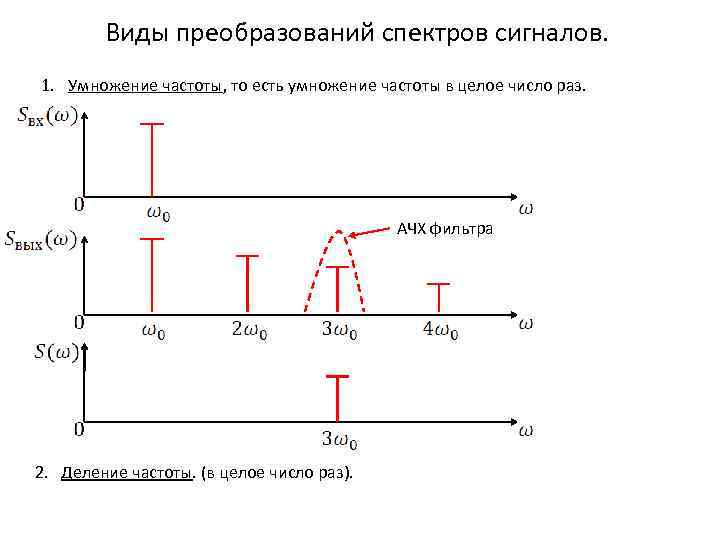Виды преобразований спектров сигналов. 1. Умножение частоты, то есть умножение частоты в целое число раз. АЧХ фильтра 2. Деление частоты. (в целое число раз).

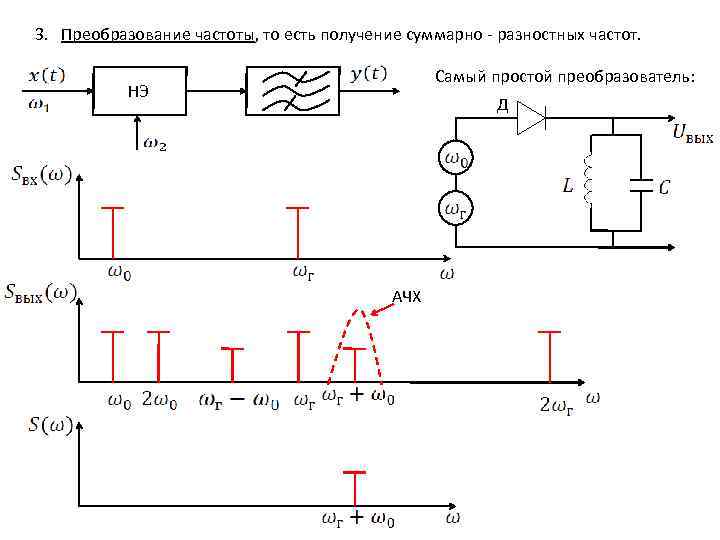3. Преобразование частоты, то есть получение суммарно - разностных частот. Самый простой преобразователь: НЭ Д АЧХ

Если , то сигнал широкополосный. Если , то сигнал узкополосный. Модулированные колебания меньше искажаются в канале связи, чем Н. Ч. сигналы, так как Н. Ч. относительно широкополосные, а Модулированные – узкополосные. Вывод: 1. Преобразования используются для борьбы с искажениями. 2. При преобразованиях можно использовать частотную селекцию, которая используется в многоканальных системах связи.

4. Модуляция. В технике связи сигнал на большие расстояния передаётся с помощью модуляции (с использованием вспомогательного переносчика), то есть вспомогательного несущего колебания. При модуляции происходит перенос низкочастотного спектра в область высоких частот. Модулированные колебания меньше искажаются в каналах связи, так как они высокочастотные и узкополосные. Модуляция – управление одним или несколькими, параметрами несущего колебания. Существует: Амплитудная Модуляция (АМ), Частотная Модуляция (ЧМ) и Фазовая Модуляция (ФМ). 5. Детектирование. АМ ЧМ ФМ Детектирование – преобразование, обратное модуляции. При детектировании Выясняется по какому параметру была проведена модуляция.

Амплитудно-модулированные сигналы. При АМ амплитуда ВЧ колебания изменяется по закону передаваемого НЧ колебания. ВЧ колебание: ? . ? . НЧ колебание: ? . ? . ? . Учитывая ? . ? . , ? . ? . и ? . ? . Получим ? . ? . В формуле ? . ? . - коэффициент глубины модуляции. ? . ? .

Если модулирующий сигнал более сложной формы(не гармоническое колебание). Огибающая изменяется в соответствии с формой модулирующего сигнала.

Дискретная Амплитудная Модуляция(ДАМ). Телеграфный сигнал.

Спектральное и векторное представление АМ. Спектральное представление: Полоса частот: Ширина спектра АМ колебания в 2 раза больше, чем ширина спектра модулирующего колебания. ? . ? .

Векторное представление: - Фаза колебаний (пройденный путь). - Угловая скорость изменения фазы. Принято при изображении модулирующего колебания вектор несущей считать неподвижным, а векторы боковых составляющих строятся из конца вектора несущего.

Модулированный вектор Модулирующий вектор Модулированный вектор ; Вывод: Аналитическое, спектральное и векторное представление АМ сигнала равноценны и полностью его определяют.

Спектр АМ колебания при модуляции сообщением сложной формы. 1. Сигнал периодический. 2. Сигнал непериодический. Сигнал периодический. - периодический сигнал. - модулирующий сигнал. можно разложить в ряд Фурье. Количество гармоник по теореме Котельникова: Основная частота (первая гармоника): АМ колебание с учётом : Порциональные коэффициенты глубины модуляции: ? . ? .

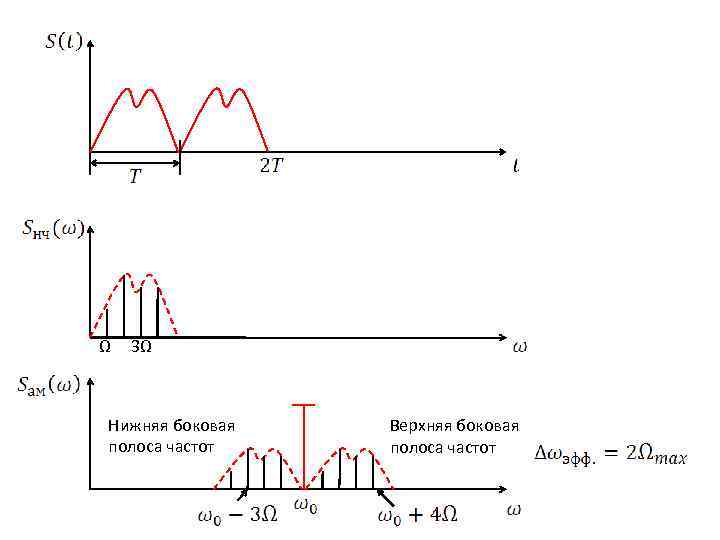Ω 3Ω Нижняя боковая полоса частот Верхняя боковая полоса частот

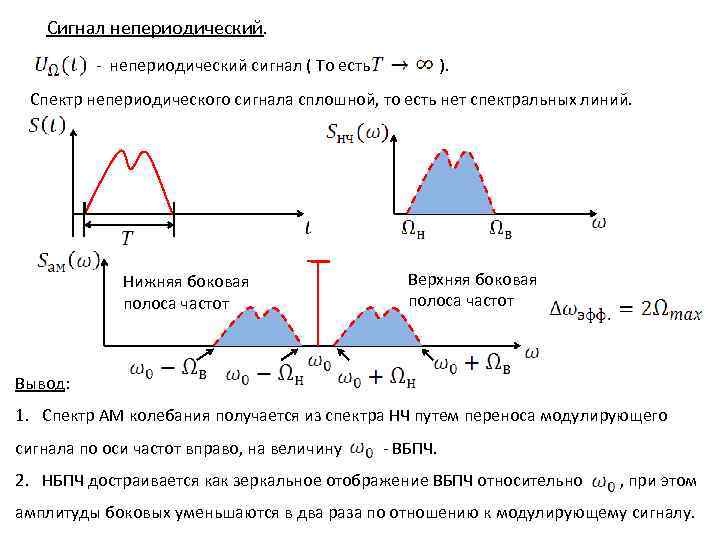Сигнал непериодический. - непериодический сигнал ( То есть ). Спектр непериодического сигнала сплошной, то есть нет спектральных линий. Нижняя боковая полоса частот Верхняя боковая полоса частот Вывод: 1. Спектр АМ колебания получается из спектра НЧ путем переноса модулирующего сигнала по оси частот вправо, на величину - ВБПЧ. 2. НБПЧ достраивается как зеркальное отображение ВБПЧ относительно , при этом амплитуды боковых уменьшаются в два раза по отношению к модулирующему сигналу.

Амплитудная модуляция с подавленной несущей (балансная). Из смысла модуляции понятно что, информация заложена только в боковые полосы, а несущее колебание информации не несёт.

Оценим выигрыш при подавлении несущей. ? . ? . определяет мощность: Где в формуле ? . ? . Т – период наблюдения. Из равенства Парсеваля для периодического сигнала: Средняя мощность на сопротивлении R: Тогда ? . ? . ? .

Суммарная мощность АМ: ? . ? . Вывод: 1. Мощность боковых равна половине мощности несущей(При ). 2. Подавление несущей даёт большой энергетический выигрыш. 3. Сэкономленную мощность можно направить на увеличение мощности одной из боковых полос, что даёт улучшение качества связи.

Однополосная Амплитудная Модуляция. Поскольку боковые полосы несут одну и ту же информацию, возникает желание подавить одну из боковых, что даёт экономию мощности или увеличение мощности боковых. Также уменьшается полоса частот, это положительный момент. ОБП с подавленной несущей ? . ? . Полностью подавлять несущие нельзя.

Получение АМ колебаний. Модулятор – устройство позволяющее получить модулированное колебание. В результате модуляции появляются новые частоты (при воздействии на НЭ). Среди новых частот есть вредные и полезные частоты. Полезные частоты выделяются с помощью фильтров. Функциональная схема. НЭ В качестве модулятора используют диод или транзистор.

Форма АМ сигнала с подавленной несущей (балансная модуляция). ? . ? . НБЧ ВБЧ ? . ? . Модулированное Б. М. колебание получается перемножением Н. Ч. сигнала и В. Ч. сигнала.

Огибающая сигнала Б. М. не повторяет форму модулирующего сигнала. Замечание: При детектировании Б. М. сигнала на приёме необходимо восстановить для нормальной работы детектора.

Принципиальная схема модулятора на диоде. Источник задаёт рабочую точку. - Ёмкостное сопротивление. , где -комбинационные частоты АЧХ фильтра

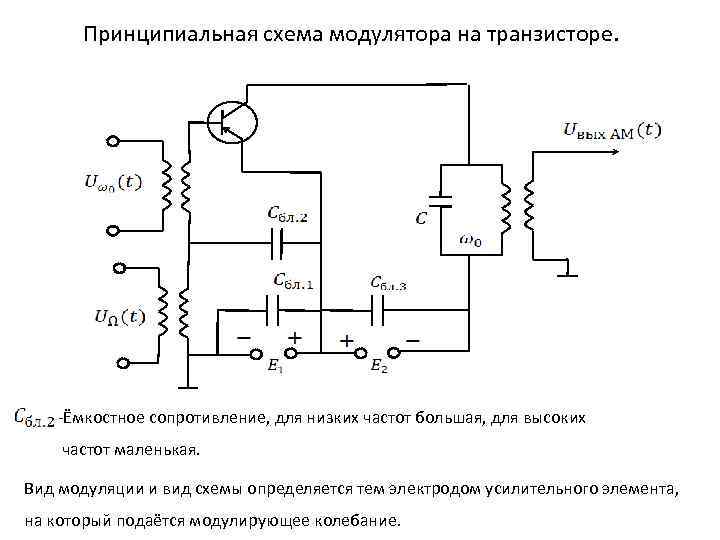Принципиальная схема модулятора на транзисторе. -Ёмкостное сопротивление, для низких частот большая, для высоких частот маленькая. Вид модуляции и вид схемы определяется тем электродом усилительного элемента, на который подаётся модулирующее колебание.

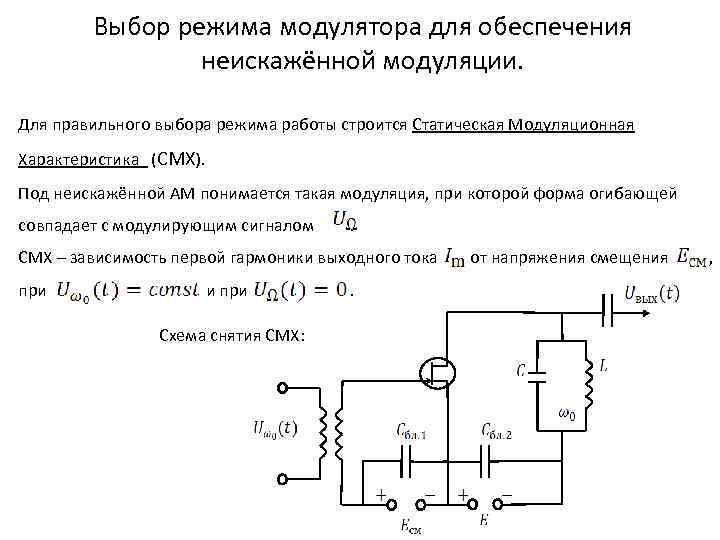Выбор режима модулятора для обеспечения неискажённой модуляции. Для правильного выбора режима работы строится Статическая Модуляционная Характеристика (СМХ). Под неискажённой АМ понимается такая модуляция, при которой форма огибающей совпадает с модулирующим сигналом . СМХ – зависимость первой гармоники выходного тока при и при Схема снятия СМХ: . от напряжения смещения ,

Линейный участок I I I На контуре огибающая

РТ на СМХ выбирается следующим образом: 1. Определяем границы линейного участка. 2. На середине линейного участка выбирается РТ. 3. Выбирается допустимая амплитуда модулирующего сигнала. Замечание: Выбор за пределами линейного участка приводит к нелинейным искажениям (ограничению сверху или снизу). РТ смещена вправо. РТ смещена влево.

Балансный модулятор. В этой схеме состоит из и . ? . ? . ? . Подставив ? . ? . и ? . ? . в ? . ? . получим: ? . ? . ? . От вычтем и получим ток нагрузки : Замечания: 1. Такая схема называется двухтактной схемой. 2. Балансный модулятор может быть реализован только в двухтактной схеме. ? . ? .

1 -й случай: Где - спектр тока, протекающего через нагрузку. АЧХ колебательного контура

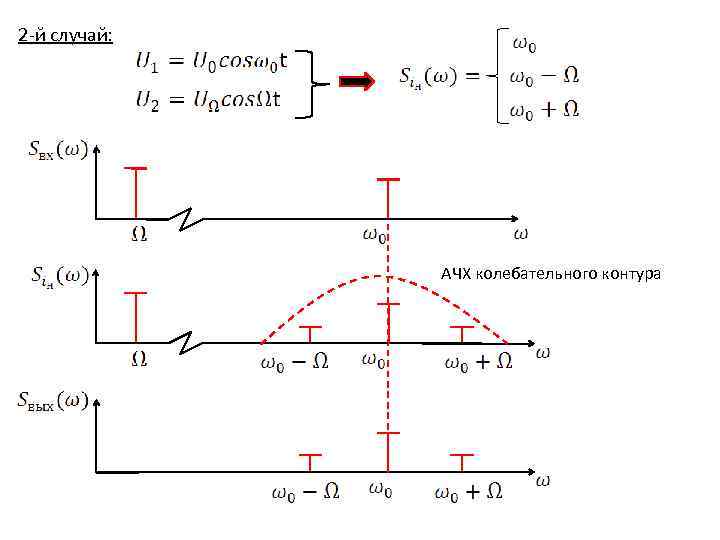2 -й случай: АЧХ колебательного контура

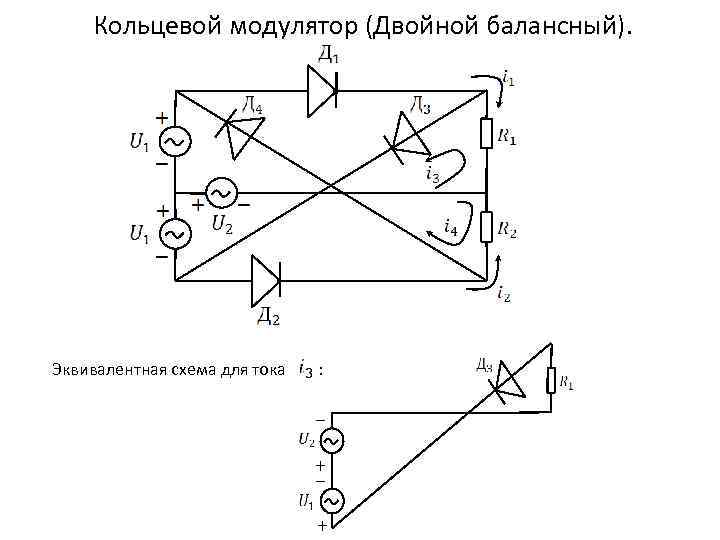Кольцевой модулятор (Двойной балансный). Эквивалентная схема для тока :

Найдем ток нагрузки решив систему: Получим: ? . ? . ? . Вывод: 1. В спектре тока будут только комбинационные частоты. 2. Не нужен колебательный контур. 3. Данная схеме инвариантна по отношению к и .

Применение кольцевого модулятора. 1. Получение балансной модуляции. 2. Получение одной боковой полосы (ОБП). либо 3. Используется для преобразования частот или . 4. Для измерения разности фаз. ; ; ; НЧ Элементарный ФНЧ: ВЧ С помощью ФНЧ избавляемся от ВЧ. 5. В качестве синхронного фазового детектора.

Амплитудные модуляторы на ИМС. В основе получения БМ лежит операция перемножения, поэтому в основе АМ на ИМС лежат перемножители. Умножитель: Вход 1 Х Выход Вход 2 Аналоговые перемножители (АП) Модуляторы на ИМС КР 140 МА 1 Квадратичные перемножители К 525 ПС 1 ПС 2 ПС 3

Алгоритм: Где - выходное напряжение, - входные сигналы, - коэффициент пропорциональности. Вход Х Вход Y Х Y Выход Z Важнейшие параметры: 1. Диапазон входных и выходных напряжений. 2. Диапазон частот поступающих сигналов. 3. Нелинейные искажения по входу. 435 МА 1 – диодный мост(интегральная схема кольцевого модулятора)

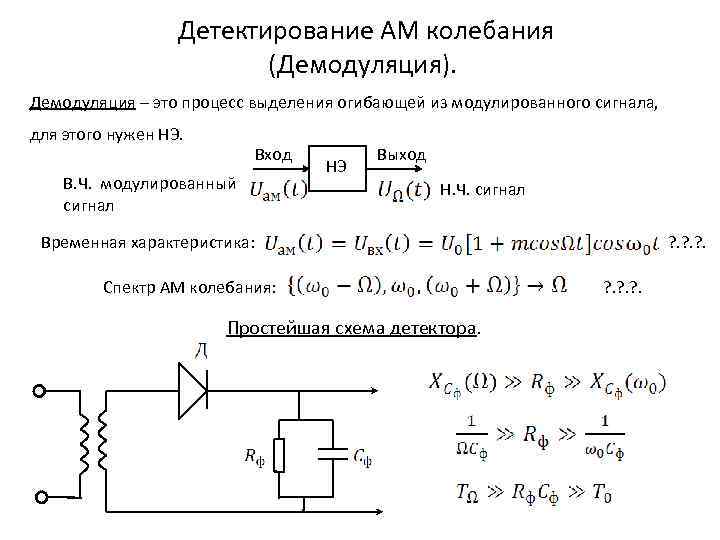Детектирование АМ колебания (Демодуляция). Демодуляция – это процесс выделения огибающей из модулированного сигнала, для этого нужен НЭ. Вход В. Ч. модулированный сигнал НЭ Выход Н. Ч. сигнал Временная характеристика: Спектр АМ колебания: Простейшая схема детектора. ? . ? . ? .

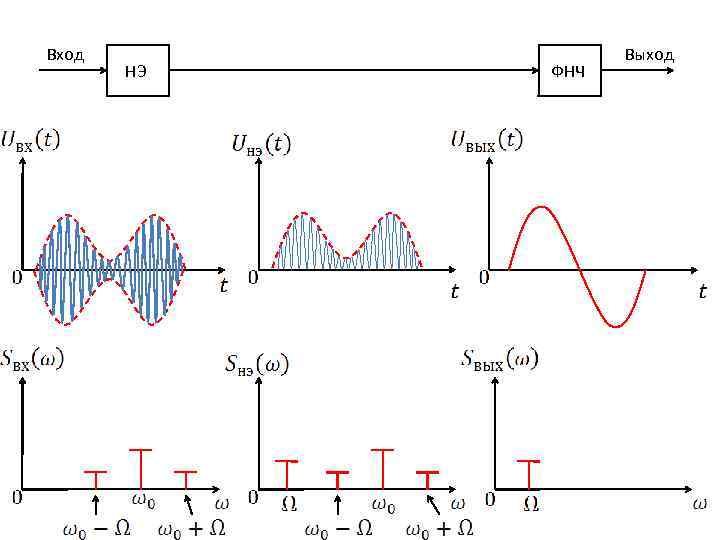Вход НЭ ФНЧ Выход

Качество работы детектора определяется характеристикой детектирования (ХД): Для АМ: Для ЧМ: ВАХ диода (детектора). зона: - зона квадратичного детектирования. - зона линейного детектирования. Уровень входного сигнала определяет в какой зоне мы работаем.

Квадратичный детектор (Работа в -й зоне). Запишем ВАХ диода квадратичным полиномом: Так как операция нелинейная, то и можно не учитывать, тогда ? . ? . Подаём модулированный сигнал: ? . ? . а b Тогда подставив ? . ? получим с : ? . ? . Составляющих , отфильтровываем ФНЧ. , не будет, поскольку это высокие частоты, и мы их

В результате подстановки и преобразования получим Н. Ч. составляющие: I I В квадратичном детекторе кроме полезного продукта есть вредная составляющая . Это приводит к искажению сигнала на выходе детектора по отношению к модулирующему. Количественной мерой искажений является Коэффициент нелинейных искажений: I I При , - очень много. Вывод: Квадратичный детектор для детектирования АМ сигналов не применим из-за большого ? . ? .

Применение квадратичного детектора. 1. Когда . 2. Для детектирования Дискретной Амплитудной Модуляции (ДАМ). 3. При детектировании одной боковой полосы (ОБП). 4. Для детектирования биений. ? . ? . и - близкие, т. е. ? . ? .

Продукты преобразования при детектировании. Спектры сигнала на входе детектора: Ток протекающий через детектор содержит: 1. Полезный продукт. 2. Вредный продукт. 3. ВЧ составляющие. и Замечание: Чтобы выделить необходимо иметь приёме необходимо восстановить . В случае приёма сигнала ОБП или БМ на . Поэтому несущая полностью не подавляется.

Линейное детектирование. Работаем во второй зоне. ? . ? . ? . - Крутизна вольт – амперной характеристики [м. А / В] Линейные детекторы различаются: 1. Детектор класса “В”, 2. Детектор класса “С”,

Детектор класса “В”. I I - Коэффициент Берга

Рассмотрим спектр на нагрузке: Схема детектора класса “В”. Выход Недостатки: Маленький коэффициент передачи.

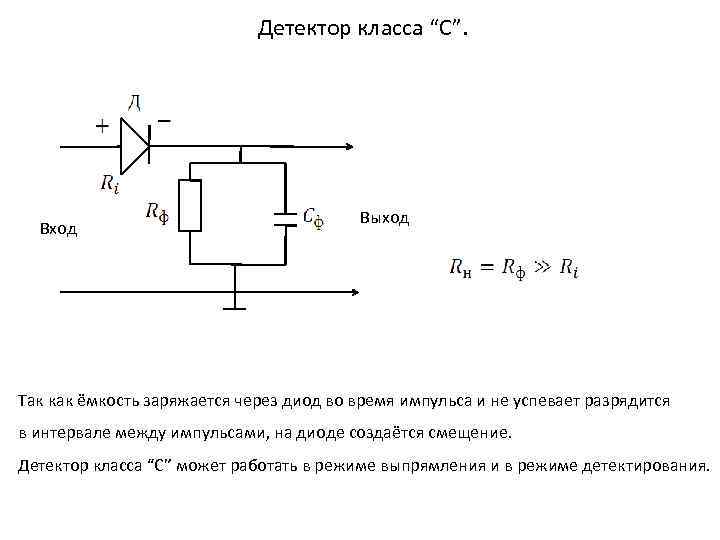Детектор класса “С”. Вход Выход Так как ёмкость заряжается через диод во время импульса и не успевает разрядится в интервале между импульсами, на диоде создаётся смещение. Детектор класса “С” может работать в режиме выпрямления и в режиме детектирования.

Режим выпрямления.

Режим детектирования. огибающая Если , то

Требования к параметрам фильтра Заряд и . - нормальная Разряд Возникают пульсации Не успеваем отслеживать огибающую

Угловая модуляция (Частотная и фазовая). Временное, спектральное и векторное представление сигналов угловой модуляции. Меняем получаем АМ. Меняем получаем ЧМ. Меняем получаем ФМ.

Фазовая модуляция. ; ; - девиация фазы. (Изменение). То есть максимальное отклонение фазы от среднего значения. Аналитическое представление: Где в формуле ? . ? . - индекс фазовой модуляции. Векторное представление: ? . ? . ? .

Частотная модуляция. ; ? . ? . Частоту в таком виде (? . ? . ) изменить нельзя, поэтому вводится понятие мгновенной частоты . ? . ? . - девиация частоты. (Изменение). То есть максимальное отклонение частоты от среднего значения. ? . ? . ? . Где в формуле ? . ? . Если и - индекс частотной модуляции. , то ? . ? . ? .

Сравнение ФМ и ЧМ. 1. При модуляции чистым тоном или одной частотой , временные функции одинаковые и не отличаются одна от другой. 2. Поскольку в ФМ , а А в ЧМ: , то Индекс , и , то , и , а обратно пропорционален . 3. Поскольку . . не зависит от модулирующей частоты модулирующей частоте , и получить из ФМ и наоборот. , то благодаря такой связи ЧМ можно

4. Спектры ЧМ и ФМ. Поскольку , то спектры ЧМ и ФМ имеют существенные различия. ЧМ a) b) ФМ . . При ЧМ при увеличении частоты расстояние между спектрами увеличивается.

Модуляция сигналов произвольной формы. ЧМ ФМ

Спектры при угловой модуляции. Существует два случая УМ: 1. - узкополосная модуляция. 2. - широкополосная модуляция. ( ШП УМ ) ( УП УМ ) Рассмотрим 1 -й случай: ? . ? . ? . Учитывая ? . ? . , и произведя известные математические операции, выражение ? . ? . примет следующий вид: ? . ? . Выражение ? . ? . напоминает спектр АМ колебания, но отличается тем, что отрицательная составляющая имеет поворот на .

АМ УМ Выводы: 1. Отличие УМ от АМ в том, что модулирующий вектор всегда перпендикулярен вектору несущей. 2. При УМ результирующий вектор “качается” относительно вектора несущей в обе стороны на величину . 3. При УП УМ присутствует паразитная АМ.

Рассмотрим 2 -й случай: ? . ? . Разложим функции I и в ряд Бесселя: I I ? . ? .

Учитывая, что I , I и подставив ? . ? . , ? . ? . в ? . ? . получим: I I I ? . ? .

Вывод: 1) Спектр ШП УМ бесконечно широкий. 2) Колебание частоты несёт информацию об (о модулирующем сигнале) наравне с другими спектральными составляющими при некоторых 3) Практическая ширина спектра определяется , . . Обычно спектральными составляющими с пренебрегают из-за их малости. Полоса частот , а при Практическая ширина спектра – область полосы, где содержится Для ЧМ , где - девиация частоты. Девиация – максимальное отклонение частоты от её среднего значения. . энергии.

Различия и сходства ЧМ и ФМ. 1. В обоих случаях не зависит от . 2. Ширина спектра при ЧМ не зависит от частоты модулирующего колебания и равна удвоенной девиации. 3. При ФМ ширина спектра пропорциональна частоте модулирующего колебания. 4. При ФМ количество спектральных линий не меняется и составляет . 5. При ЧМ количество спектральных линий меняется, но полоса частот, в которой сосредоточена основная доля энергии сигнала неизменна.

Методы получения сигналов угловой модуляции. Различают два метода: 1. Прямой метод получения. 2. Косвенный метод получения. Прямой метод – непосредственное воздействие на частоту или фазу задающего генератора(то есть на генератор, который даёт ). Косвенный метод – получение ЧМ или ФМ из других видов модуляции(ФМ из АМ, а ЧМ из ФМ).

Прямой метод получения ЧМ. Задающий Генератор ? . ? . Выход Если и Для ЧМ: a) . b) . , то

З. Г. Z Выход

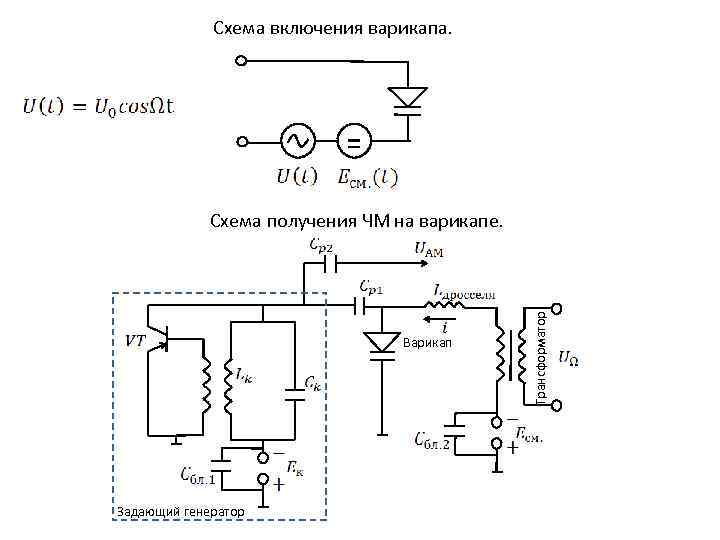Схема включения варикапа. Варикап Задающий генератор Трансформатор Схема получения ЧМ на варикапе.

Назначение элементов в схеме получения ЧМ на варикапе. - Разделительная ёмкость, для того, чтобы не пропускать постоянную составляющую. Велико, для подачи смещения на варикап и для исключения шунтирования колебательного контура низкоомной цепью модулятора. - Блокировочная ёмкость, если её не поставить, то будет присутствовать фон. ? . ? . ? . Где в формуле ? . ? . - Ёмкость варикапа в рабочей точке, при отсутствии модуляции, - Изменение ёмкости при подаче на варикап модулирующего сигнала.

? . ? . - ёмкость контура при отсутствии модулирующего сигнала. ; - Резонансная частота контура при отсутствии модуляции. ; ; - Коэффициент изменения ёмкости. Тогда, с учетом всех преобразований, получим: ? . ? .

Недостатки прямого метода: 1. Исключена возможность стабилизации частоты генератора, а она должна быть стабильна. 2. Невысокая девиация частоты из-за малого линейного участка изменения ёмкости Примечание: Девиация частоты может быть увеличена за счёт умножения. .

Прямой метод получения ФМ. Сущность получения ФМ: Используется не задающий генератор, а усилитель к которому подключается эквивалентная реактивность. З. Г. Усили. Ус тель - Эквивалентная реактивность

- уменьшилась Для изменения результирующей частоты контура используются транзисторные реактивности(ёмкости).

Косвенный метод получения ЧМ. Основан на получении одних видов модуляции из других с учётом их сходства и различия. 1. ЧМ из ФМ. 2. ФМ из ЧМ. 3. ЧМ и ФМ из АМ. 1. Получение ЧМ из ФМ. Вход Ф. М. 2. Получение ФМ из ЧМ. Вход Ч. М.

3. Получение ЧМ и ФМ из АМ. Такая возможность основывается на сходстве и различии спектральных и векторных диаграмм сигналов АМ и УМ. Б. М. Σ

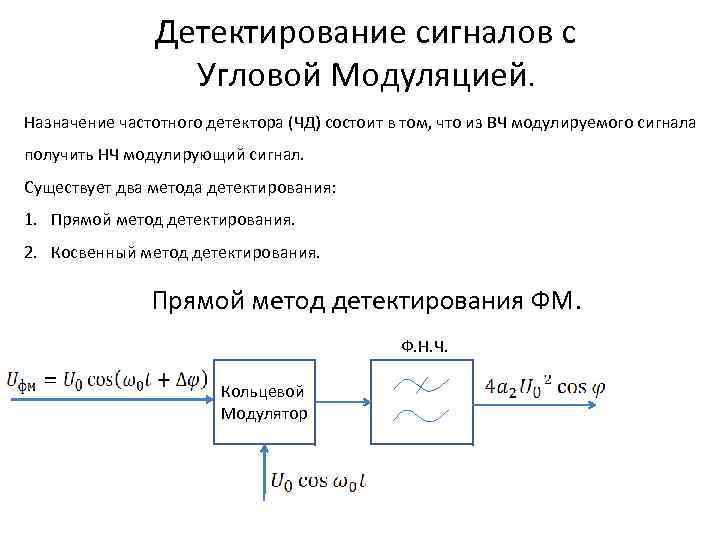Детектирование сигналов с Угловой Модуляцией. Назначение частотного детектора (ЧД) состоит в том, что из ВЧ модулируемого сигнала получить НЧ модулирующий сигнал. Существует два метода детектирования: 1. Прямой метод детектирования. 2. Косвенный метод детектирования. Прямой метод детектирования ФМ. Ф. Н. Ч. Кольцевой Модулятор

Детектирования ЧМ. Поскольку модулирующий сигнал стоит под знаком интеграла, то прямого метода детектирования ЧМ сигнала нет. Существует два варианта детектирования ЧМ: 1. ЧМ ФМ – детектирование ФМ (Фазовый детектор). 2. ЧМ АМ – детектирование АМ (Амплитудный детектор). Возможны следующие методы детектирования ЧМ колебания: 1. На одном расстроенном контуре. 2. На двух расстроенных контурах. 3. На одном настроенном контуре.

1. На одном расстроенном контуре.

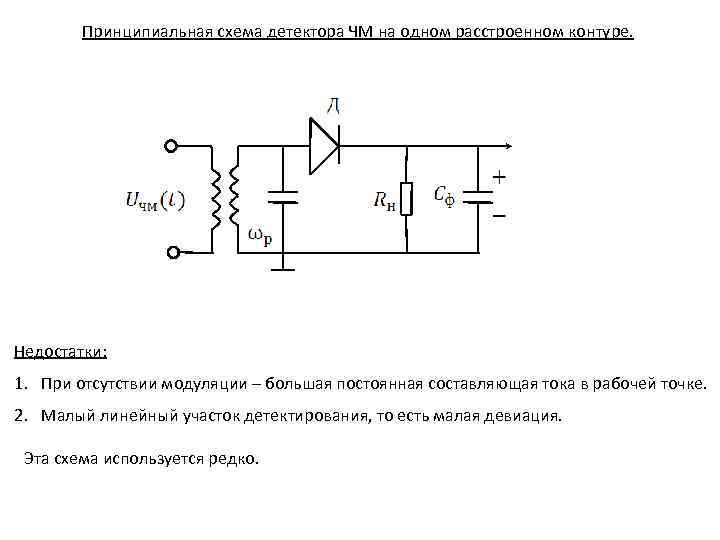Принципиальная схема детектора ЧМ на одном расстроенном контуре. Недостатки: 1. При отсутствии модуляции – большая постоянная составляющая тока в рабочей точке. 2. Малый линейный участок детектирования, то есть малая девиация. Эта схема используется редко.

2. На двух взаимно – расстроенных контурах. Так как диоды подключаются встречно.

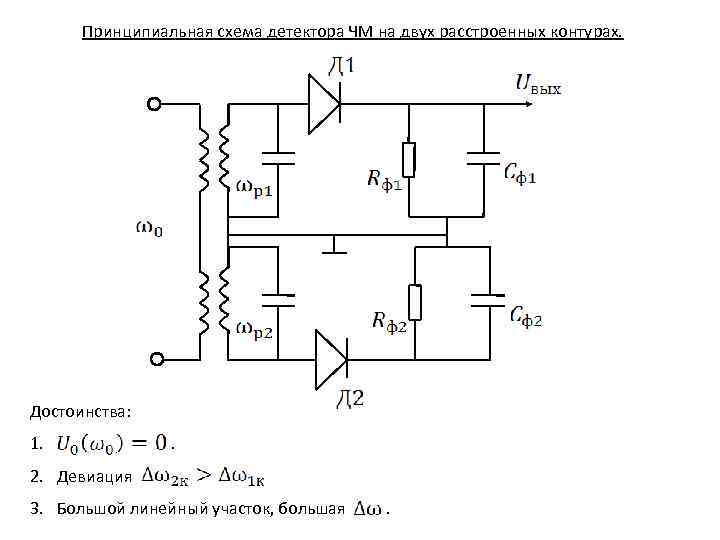Принципиальная схема детектора ЧМ на двух расстроенных контурах. Достоинства: 1. . 2. Девиация 3. Большой линейный участок, большая .

Фазовый Детектор (ФД). Фазовый (Синхронный) детектор позволяет осуществлять высококачественное детектирование сигналов АМ, ЧМ, ФМ. Он обеспечивает наилучшее выделение сигнала на фоне помех. Синхронный детектор Вход Выход Опорный генератор У синхронного детектора два входа, на первый подаётся модулированный сигнал на второй вход подаётся опорное напряжение сигнала и и , , при этом частоты приходящего должны совпадать (синхронность). Фазы приходящего сигнала тоже должны совпадать (синфазность). Совпадение фазы осуществляется фазовой автоподстройкой системы синхронизации.

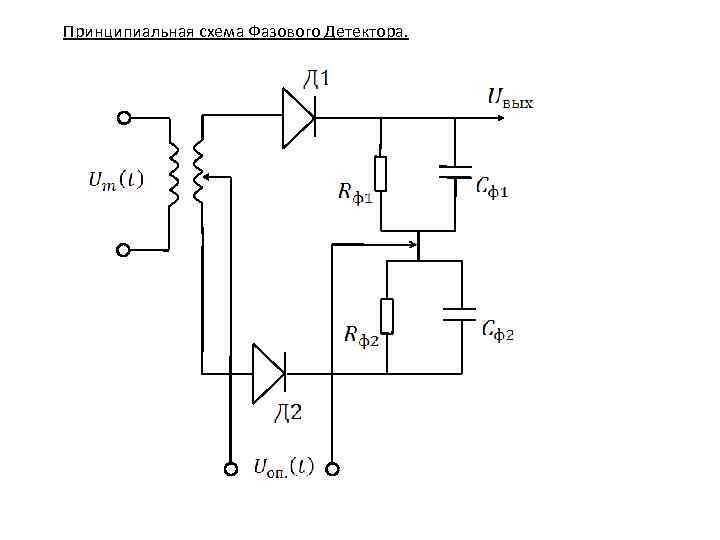Принципиальная схема Фазового Детектора.

Принцип работы Фазового Детектора. ? . ? . Поскольку опорный сигнал постоянен по амплитуде, то качество детектирования получается без искажений.

Модуляция Дискретными Сигналами. Дискретные виды модуляции. 1. Дискретная Амплитудная Модуляция (ДАМ). 2. Дискретная Частотная Модуляция (ДЧМ). 3. Дискретная Фазовая Модуляция (ДФМ). 4. Дискретная Относительная Фазовая Модуляция (ДОФМ). ДАМ и ДФМ практически не используются в связи, ДАМ используется в локации.

Временные спектральные представления дискретных сигналов. Ранее рассматривались различные виды модуляции сигналов, сейчас широко используют дискретные виды модуляции. При этом, передаваемое сообщение передаётся в виде последовательности прямоугольных импульсов(кодовая комбинация). Источник АЦП 101101 Модулятор Передатчик

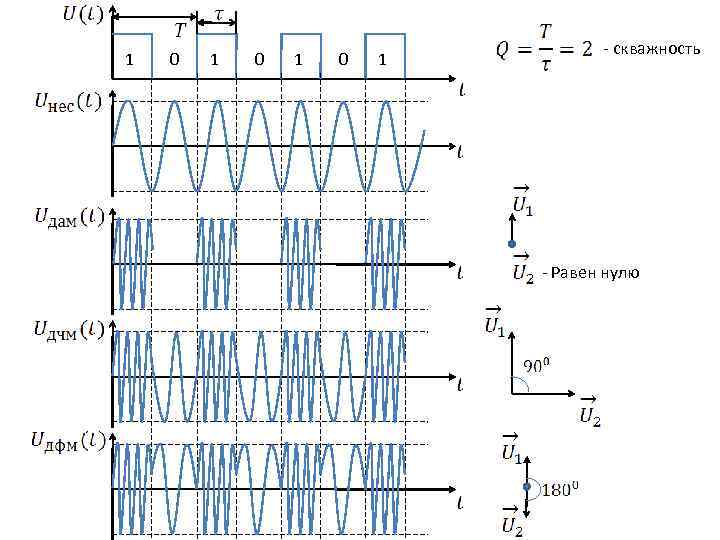1 0 1 0 1 - скважность - Равен нулю

Дискретно-амплитудная модуляция. ДАМ: Дискретно-частотная модуляция. ДЧМ: Дискретно-фазовая модуляция. ДФМ: Для максимальной различимости нужно чтобы:

Примечание: Существует два варианта образования ДЧМ: 1. Без разрыва фазы. 2. С разрывом фазы. Без разрыва фазы С разрывом фазы

Спектры сигналов дискретной модуляции. Они получаются на основе общего правила построения спектров модулированных сигналов, то есть спектр НЧ переносят из области низких частот переносят в область высоких частот. Пояснение: Для понимания вида спектра ДЧМ полезно рассматривать его как сумму двух спектров ДАМ с поднесущими В ДФМ при При и , , . . .

Возьмем скважность: 1 0 0 1 1 0 0 Выводы: - основная спектральная частота. - скважность, определяет гармоники - огибающая частота. , которые равны нулю.

Дискретная относительная фазовая модуляция(ДОФМ). ДФМ обеспечивает максимальную помехоустойчивость за счёт расстояния между сигналами. Однако при детектировании сигнала ДФМ возникают большие трудности из-за необходимости поддержания равенства фаз опорного генератора. Если равенство фаз нарушено, то возникает «обратная работа» , то есть получает « 0» вместо « 1» или « 1» вместо « 0» . Это происходит, потому что, информация о переданном сигнале содержится в начальной фазе передаваемого сигнала, а приём происходит при сравнении фазы принимаемого сигнала и опорного генератора.

При использовании ОФМ применяется относительное кодирование на стороне передачи и относительная демодуляция на стороне приёма. Сигнал от кодера Модулятор ДФМ 101010 Линия задержки Приём сигналов ОФМ при демодуляции осуществляется двумя способами: 1. Когерентный приём – сравнение полярностей. 2. Некогерентный приём – сравнение фаз.

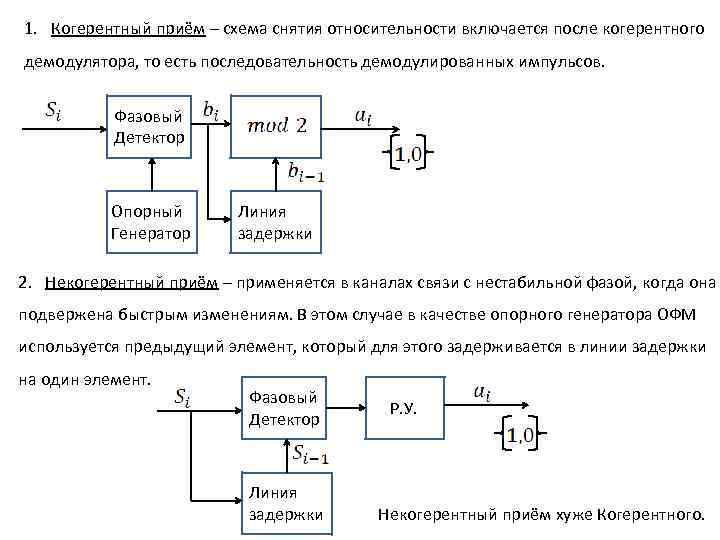1. Когерентный приём – схема снятия относительности включается после когерентного демодулятора, то есть последовательность демодулированных импульсов. Фазовый Детектор Опорный Генератор Линия задержки 2. Некогерентный приём – применяется в каналах связи с нестабильной фазой, когда она подвержена быстрым изменениям. В этом случае в качестве опорного генератора ОФМ используется предыдущий элемент, который для этого задерживается в линии задержки на один элемент. Фазовый Детектор Линия задержки Р. У. Некогерентный приём хуже Когерентного.

Импульсные виды модуляции. В технике связи наряду с гармоническим переносчиком широко используется периодические последовательности импульсов. Возможные виды импульсной модуляции: 1. Амплитудно-импульсная модуляция (АИМ). 2. Широко-импульсная модуляция (ШИМ). 3. Фазо-импульсная модуляция (ФИМ). - Момент появления импульса.

Для ФИМ: Если , то ФИМ сдвигается влево. Если , то ФИМ сдвигается вправо. В основе импульсных методов модуляции лежит теорема Котельникова, которая определяет частоту следования импульса. где - период следования. АИМ в чистом виде не используется в силу низкой помехоустойчивости, но лежит в основе получения ИКМ.

Спектр Амплитудно-Импульсной Модуляции.

Импульсно-кодовая модуляция (ИКМ). ИКМ – один из возможных методов импульсной модуляции, который суммирует в себе все положительные свойства дискретизации, квантования и кодирования. Сущность ИКМ. Непрерывное сообщение дискретизируется по времени, по теореме Котельникова полученные отсчёты квантуются, то есть дискретизируются по амплитуде, полученная последовательность квантованных значений непрерывного сообщения кодируется в виде последовательностей кодовых комбинаций. Кодирование сводится к записи номера уровня в двоичной системе счисления. Передача отдельных значений сигнала сводится к передаче определённых групп импульсов. Эти группы импульсов передаются друг за другом через относительно большие промежутки времени по сравнению с длительностью отдельных импульсов.

Достоинства ИКМ: 1. Высокая помехоустойчивость. 2. Современная элементная база вычислительной техники. 3. Возможность приведения всех видов передаваемой информации к цифровой форме, что позволяет проводить интеграцию систем коммутации и систем передачи. 4. Цифровые системы не требуют настройки. Недостатки ИКМ: 1. Не точно передаётся функция. 2. Преобразование непрерывных сообщений в цифровую форму сопровождающее округлением мгновенных значений до ближайшего уровня квантования. Возникающая при этом погрешность неустранима, но контролируема, так как не превышает шаг квантования.

Динамический диапазон квантованных сигналов. ? . ? . Количество уровней. ? . ? . Интервал квантования. ? . ? . Мощность шума квантования (при условии, что импульсы прямоугольной формы). 8. 8. 7. Коэффициент квантования. ? . ? . , где - пикфактор(отношение максимального значения сигнала к среднеквадратическому значению). ? . ? .

Использование компадирования в ИКМ. (компрессор-сжатие). Из выражения 8. 8. 7. видно, что шум квантования не зависит от сигнала. В связи с этим при уменьшении сигнала снижается отношение и примерно построенный сигнал шума квантования , и . Чтобы получить , следовало бы использовать переменную шкалу шагоквантования: малую для малых сигналов и большую для больших сигналов. Поэтому отсчёты пропускают через так называемый компрессор с соответствующей характеристикой: преобразованный соответствующим образом в компрессоре дискрет(отсчёт), затем кодируется как при равномерном шаге. Источник Непрерывных сообщений Дискретизатор Квантователь Компрессор Кодер К модулятору передатчика На приёме кодовые комбинации подвергаются декодированию, а затем вводятся в экспандер, характеристика которого обратна компрессору.

Приёмная часть. Приёмник с Демодулятором Компандер Декодер ФНЧ К получателю Выигрыш в использовании экспандера. А Без экспандера. Выигрыш С экспандером. Точка А является граничной, с увеличением выигрыш падает, после А – проигрыш.

Система связи с Принцип работы с модуляцией состоит в том, что передаётся не информация о величинах отсчёта, а только о том, больше или меньше данный дискрет по отношению к предыдущему переданному значению, поскольку существует одна из двух возможностей(случай абсолютного равенства значений, он маловероятный, не рассматривается), поэтому информация об отсчёте может быть передана с помощью 1, если он растёт или с отсутствием сигнала, если очевидно, что указанная информация должна передаваться чаще, чем по Котельникову, как в системах ИКМ.

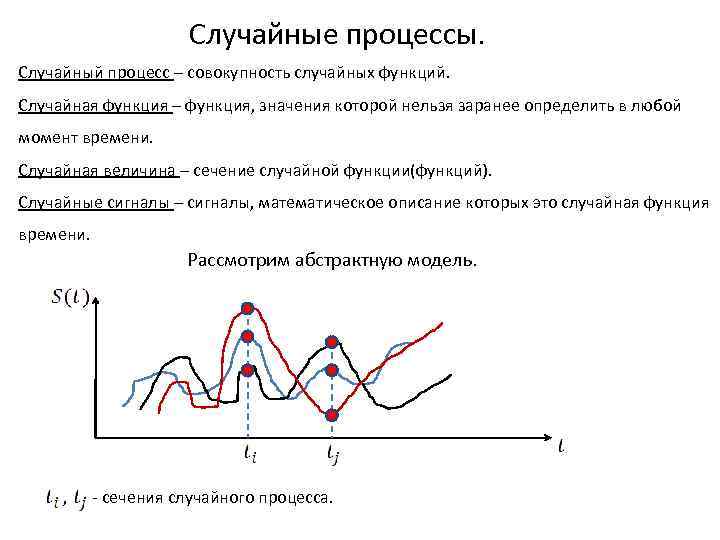Случайные процессы. Случайный процесс – совокупность случайных функций. Случайная функция – функция, значения которой нельзя заранее определить в любой момент времени. Случайная величина – сечение случайной функции(функций). Случайные сигналы – сигналы, математическое описание которых это случайная функция времени. Рассмотрим абстрактную модель. , - сечения случайного процесса.

Реализация случайного процесса(СП) – это конкретный вид, который принимает сигнал в данном испытании сечения конкретного значения реализации СП в некоторый произвольный, но фиксированный момент времени. Достоинство: Наглядность (полное представление). Недостатки: Громоздкость и сложность вычисления. Необходимо найти математические методы, описывающие СП и определить его характеристики. Для описания СП вводят случайные функции: Функция плотности вероятности(ФРВ) - , Функция Распределения Вероятности(ФРВ) - Функция Распределения Вероятности. Характеризует процесс только в одном сечении. N – мерная ФРВ характеризует распределение в N сечениях. .

Функция Плотности Вероятности. ? . ? . Интегральная ФРВ. Для N – мерной функции распределения: ? . ? . Двумерная ФРВ. Широко используется в технике связи. ? . ? .

Свойства ФРВ И ФПВ: 1. - функция неубывающая. 2. . 3. 4. 5. .

Числовые характеристики. Полное описание любого случайного процесса – N – мерная ФРВ, N – мерная ФПВ. Ограничиваются тремя видами: 1. Математическое ожидание 2. Дисперсия . 3. Функции корреляции. .

1. Математическое ожидание. Обозначение: ? . ? . Математическое ожидание – неслучайная величина времени, которая в любой момент является математическим ожиданием данного сечения, то есть это кривая геометрического места точек математического ожидания всех сечений.

2. Дисперсия. Обозначение: ? . ? . Дисперсия – математическое ожидание квадрата отклонения (среднеквадратическое отклонение).

3. Функции корреляции. Характеризуют статистическую связь между сечениями случайных процессов. Существует четыре разновидности: a) Ковариационная функция. b) Корреляционная функция. c) Нормированная функция. d) Функция взаимной корреляции. a) Ковариационная функция – математическое ожидание произведения значений случайного процесса в двух сечениях. ? . ? .

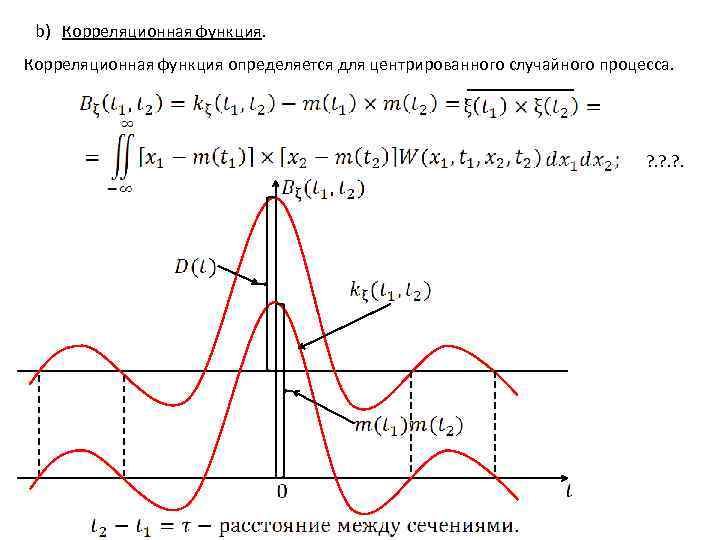b) Корреляционная функция определяется для центрированного случайного процесса. ? . ? .

c) Нормированная функция вводится для сравнения процессов между собой. ? . ? . С увеличением функции будут уменьшатся. d) Функция взаимной корреляции. Характеризует связь между сечениями разных случайных процессов. ? . ? . Замечание: Если два процесса независимы, то их функция взаимной корреляции равна нулю.

Стационарные случайные процессы. Случайные процессы Стационарные (установившиеся) Стационарные в узком смысле Нестационарные (неустановившиеся) Стационарные в широком смысле Стационарность в узком смысле – случайный процесс, у которого n-мерная ФПВ не зависит от сдвига всех сечений вправо или влево на одну и ту же величину Стационарность в широком смысле – случайный процесс , у которого числовые характеристики не зависят от времени, а функция корреляции зависит от интервала между отсчётами. Если процесс стационарен в узком смысле, то он стационарен и в широком смысле, а наоборот не всегда верно.

Свойства стационарности в узком смысле случайных процессов: 1. . 2. . 3. . 4. . 5. . Выводы: 1. Одномерная функция плотности дисперсия математическое ожидание не зависят от времени для стационарного процесса в узком смысле. 2. Двумерная плотность вероятности и функция корреляции от времени не зависит, а зависит от расстояния между отсчётами(сечениями), то есть от

Свойства функций корреляции в стационарных процессах: 1. Функция корреляции действительная и чётная, так как это функция времени. 2. . Если - Полная мощность процесса 3. - Мощность переменной составляющей 4. -Мощность постоянной составляющей

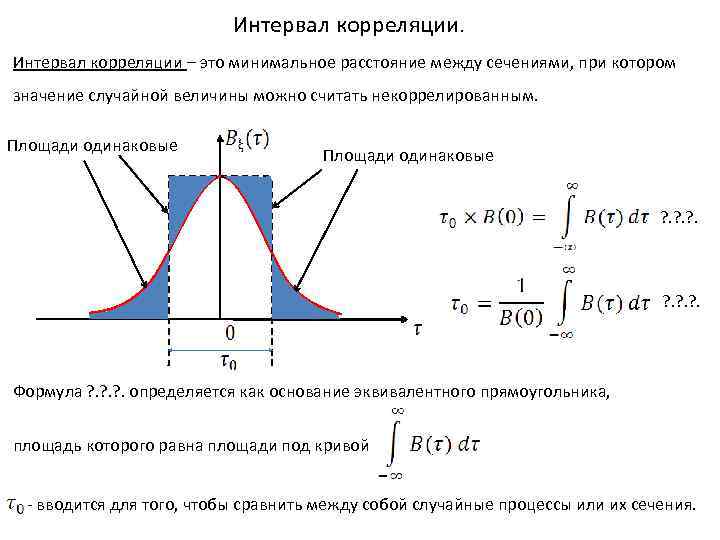Интервал корреляции – это минимальное расстояние между сечениями, при котором значение случайной величины можно считать некоррелированным. Площади одинаковые ? . ? . ? . Формула ? . ? . определяется как основание эквивалентного прямоугольника, площадь которого равна площади под кривой - вводится для того, чтобы сравнить между собой случайные процессы или их сечения.

Нормированная функция корреляции. ? . ? . ? . Если , то Все отсчёты некоррелированы, если между ними интервал . Процесс, у которого два ближних сечения при некоррелированы, не имеют статической связи.

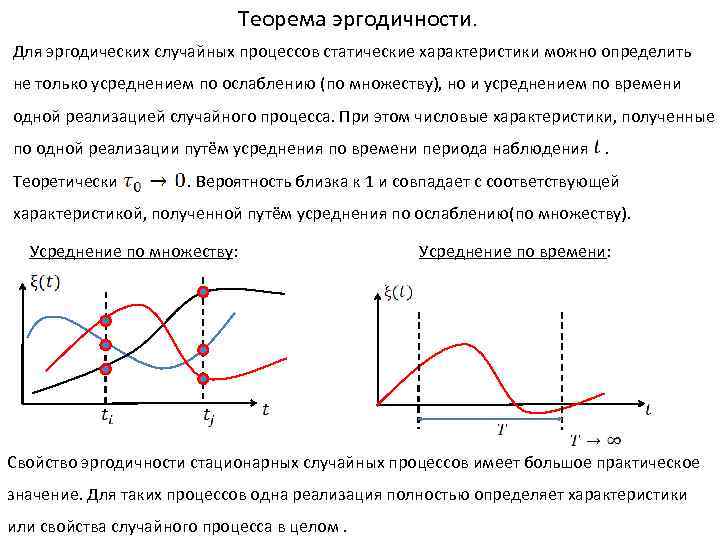Теорема эргодичности. Для эргодических случайных процессов статические характеристики можно определить не только усреднением по ослаблению (по множеству), но и усреднением по времени одной реализацией случайного процесса. При этом числовые характеристики, полученные по одной реализации путём усреднения по времени периода наблюдения. Теоретически . Вероятность близка к 1 и совпадает с соответствующей характеристикой, полученной путём усреднения по ослаблению(по множеству). Усреднение по множеству: Усреднение по времени: Свойство эргодичности стационарных случайных процессов имеет большое практическое значение. Для таких процессов одна реализация полностью определяет характеристики или свойства случайного процесса в целом.

Усреднение по множеству Усреднение по времени

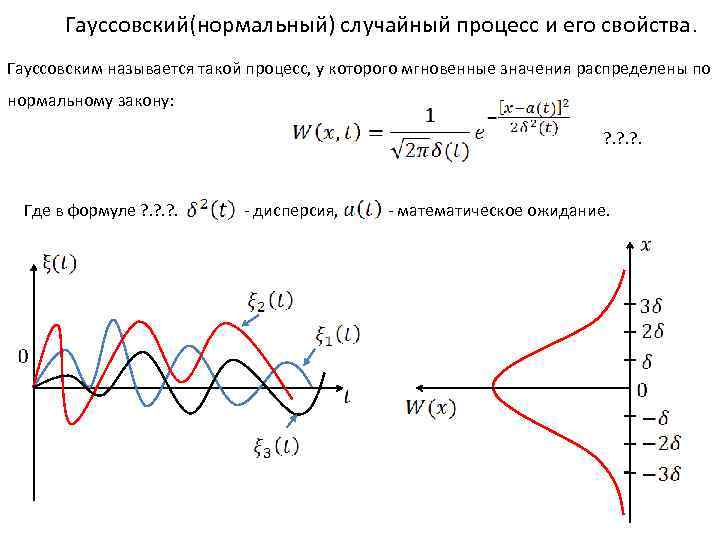Гауссовский(нормальный) случайный процесс и его свойства. Гауссовским называется такой процесс, у которого мгновенные значения распределены по нормальному закону: ? . ? . Где в формуле ? . ? . - дисперсия, - математическое ожидание.

Математическое ожидание . Если не менять Дисперсия .

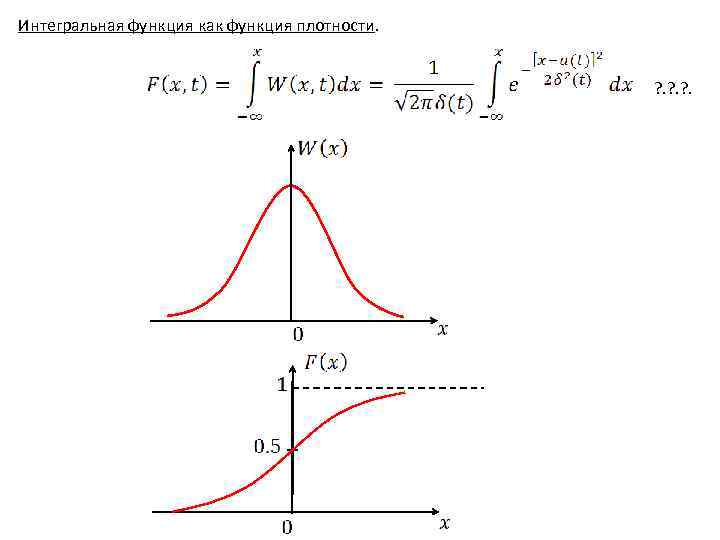Интегральная функция как функция плотности. ? . ? .

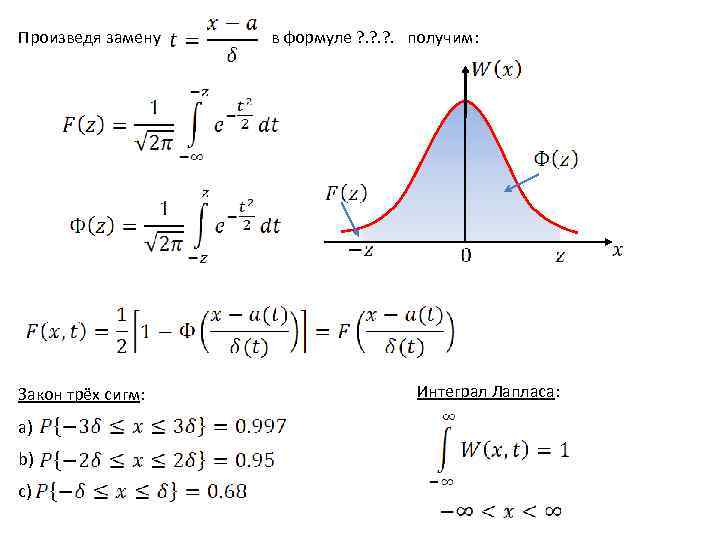Произведя замену Закон трёх сигм: a) b) c) в формуле ? . ? . получим: Интеграл Лапласа:

Свойства нормального процесса. 1. Стационарность в широком смысле эквивалентна стационарности в узком смысле. 2. Условие эргодичности: , то есть интеграл сходится. 3. Сечения независимы, если они нормированные. 4. Линейные преобразования не изменяют функции вероятности(вида кривой). 5. Сумма нормального случайного процесса и детерминированной функции не изменяет закон распределения.

Функция корреляции одиночного прямоугольного импульса. Случайные процессы могут быть периодические и непериодические.

Функция корреляции. Напишем функцию корреляции отдельно: Функция корреляции непериодическая Функция корреляции чётная.

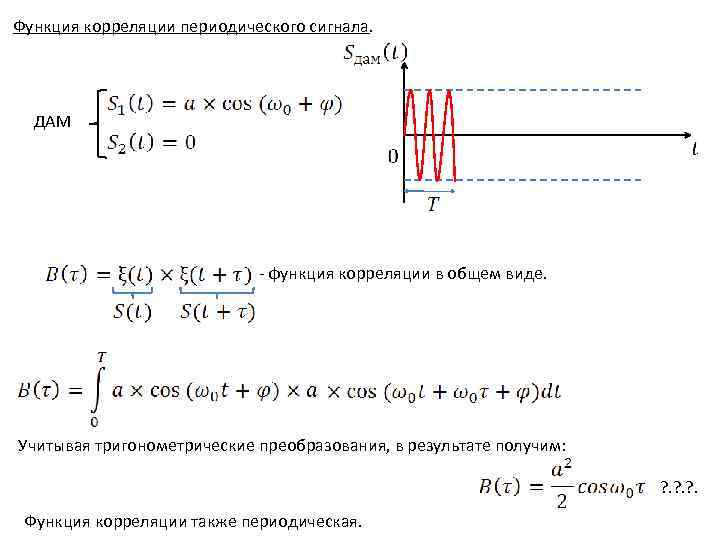Функция корреляции периодического сигнала. ДАМ - функция корреляции в общем виде. Учитывая тригонометрические преобразования, в результате получим: ? . ? . Функция корреляции также периодическая.

Функция корреляции будет иметь вид: Вывод: У периодического сигнала функция корреляции является периодической функцией с той же частотой .

Применение корреляционных методов обработки сигналов в технике связи. Устройства, позволяющие определить функцию корреляции называются корреляционными. Существует два способа приёма: 1. Взаимнокорреляционный. 2. Автокорреляционный. Рассмотрим первый способ. Интегратор от 0 до Т Решающее устройство

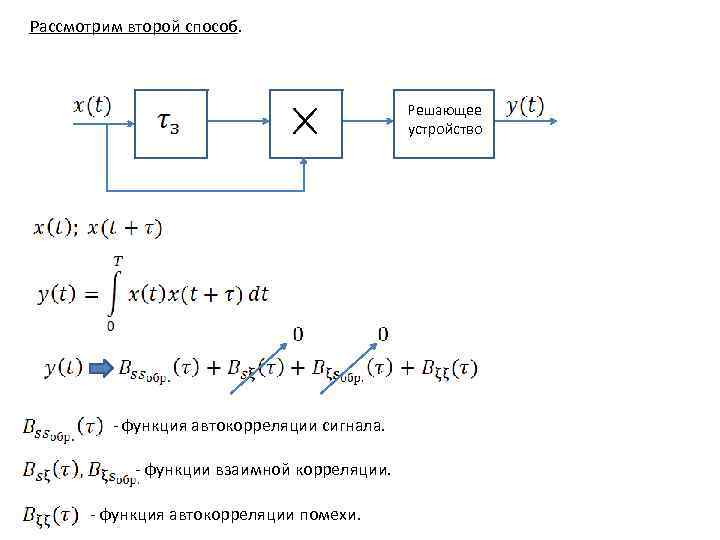Рассмотрим второй способ. Решающее устройство - функция автокорреляции сигнала. - функции взаимной корреляции. - функция автокорреляции помехи.

Мощность помехи Растёт, если Чем больше растёт. , тем лучше. Отсчет лучше делать в конце длительности сигнала.