Теория электрических цепей УЧЕБНАЯ КАРТА ДИСЦИПЛИНЫ Теория электрических

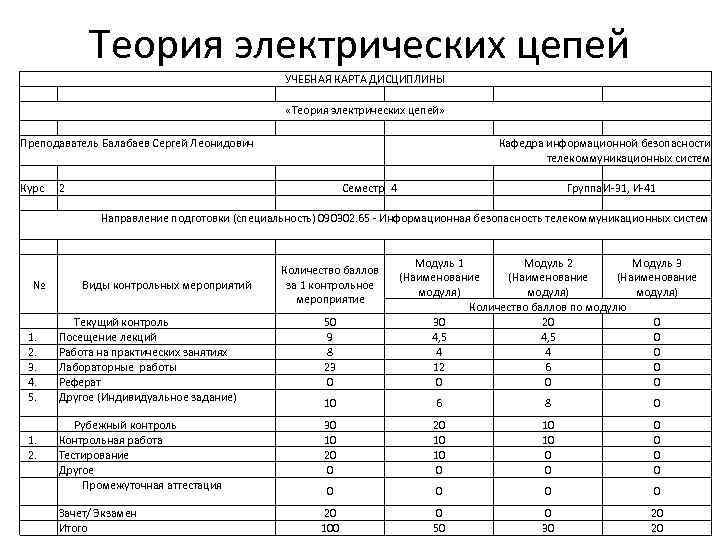
Теория электрических цепей УЧЕБНАЯ КАРТА ДИСЦИПЛИНЫ «Теория электрических цепей» Преподаватель Балабаев Сергей Леонидович Курс Кафедра информационной безопасности телекоммуникационных систем 2 Семестр 4 Группа И-31, И-41 Направление подготовки (специальность) 090302. 65 - Информационная безопасность телекоммуникационных систем № Виды контрольных мероприятий Количество баллов за 1 контрольное мероприятие Модуль 1 Модуль 2 Модуль 3 (Наименование модуля) Количество баллов по модулю 30 20 0 4, 5 0 4 4 0 12 6 0 0 Текущий контроль Посещение лекций Работа на практических занятиях Лабораторные работы Реферат Другое (Индивидуальное задание) 50 9 8 23 0 10 6 8 0 Рубежный контроль Контрольная работа Тестирование Другое Промежуточная аттестация 30 10 20 10 10 0 0 0 Зачет/ Экзамен Итого 20 100 0 50 0 30 20 20 1. 2. 3. 4. 5. 1. 2.

Операторный метод анализа переходных процессов

Классический метод анализа переходных процессов используют в основном в тех случаях, когда исследуемая цепь имеет невысокий порядок сложности, а внешнее воздействие на нее после коммутации является гармонической функцией времени либо постоянно. Если внешнее воздействие на цепь после коммутации имеет более сложный характер, то определение вынужденной составляющей реакции цепи существенно затрудняется, а при повышении порядка цепи усложняется нахождение постоянных интегрирования.

Значительно большие возможности представляет операторный метод анализа переходных процессов, основанный на применении преобразования Лапласа. Подобно ранее рассмотренному методу комплексных амплитуд, операторный метод относится к символическим методам, в которых операции над функциями времени заменяются операциями над их символами (изображениями). Взаимное соответствие между функцией времени а(t) и ее изображением А(p) в операторном методе устанавливается с помощью прямого (6. 46) и обратного (6. 47) преобразований Лапласа и указывается знаком соответствия (≑): a(t) ≑ A(p).

Функция А(p) называется операторным изображением функции а(t) или изображением функции а(t) по Лапласу. Исходная функция времени a(t) по отношению к своему операторному изображению является оригиналом. Комплексное число p будем называть оператором преобразования Лапласа или комплексной частотой

Свойства преобразования Лапласа

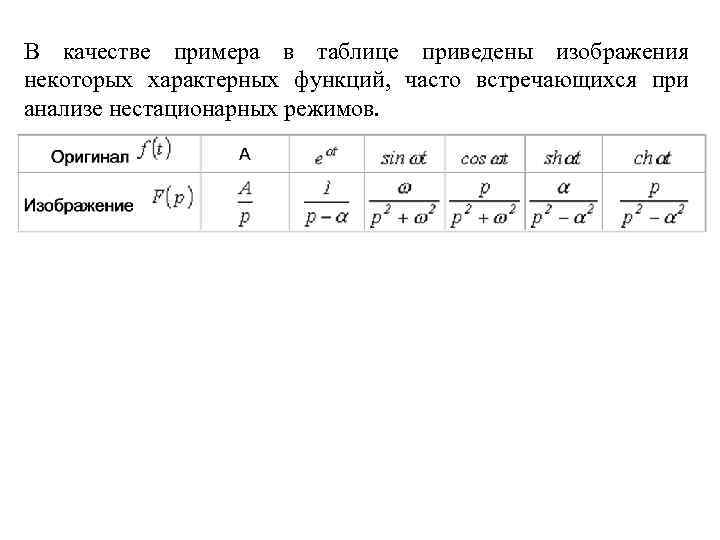
В качестве примера в таблице приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.

Уравнения электрического равновесия цепи в операторной форме. Операторные схемы замещения идеализированных двухполюсных элементов Как следует из рассмотренного материала, используя преобразование Лапласа, каждому уравнению, входящему в систему уравнений электрического равновесия цепи, можно поставить в соответствие уравнение, составленное относительно операторных изображений токов и напряжений. Уравнениям баланса мгновенных значений токов и напряжений соответствуют уравнения баланса операторных изображений токов и напряжений, а компонентным уравнениям, описывающим соотношения между мгновенными значениями токов и напряжений отдельных ветвей, — уравнения, связывающие операторные изображения токов и напряжении тех же ветвей.

Следовательно, каждому пассивному линейному двухполюснику при нулевых начальных условиях может быть поставлена в соответствие операторная схема замещения, на которой рассматриваемый двухполюсник представляется своим операторным входным сопротивлением или операторной входной проводимостью, а токи и напряжения на его зажимах — их операторными изображениями. Если в рамках решаемой задачи двухполюсник не находится при нулевых начальных условиях, то его операторная эквивалентная схема должна содержать независимый источник тока или напряжения, характеризующий начальные запасы энергии в цепи.

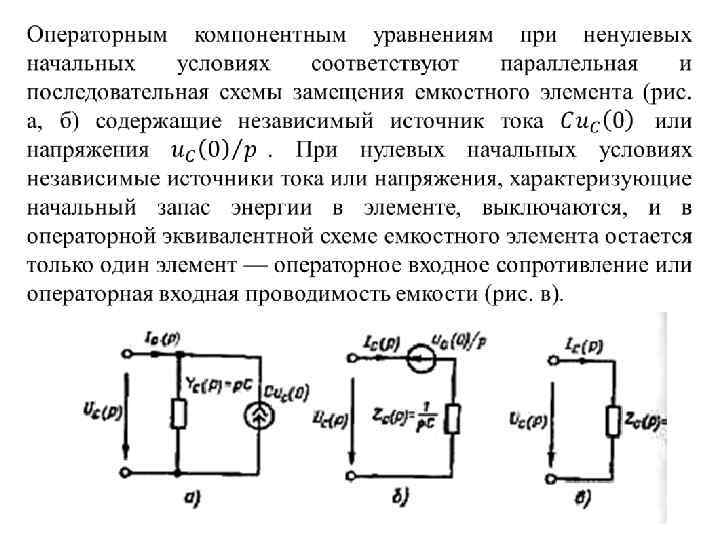
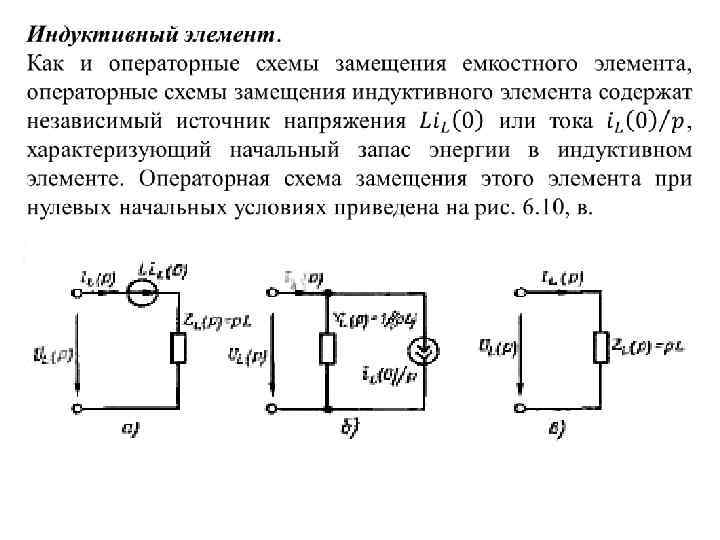
Аналогичным образом может быть найдено выражение для операторного входного сопротивления (проводимости) произвольного линейного двухполюсника, составленного из идеализированных пассивных элементов. Поэтому для преобразования операторных схем замещения линейных пассивных двухполюсников при нулевых начальных условиях можно использовать все рассмотренные ранее правила преобразования линейных пассивных цепей при гармоническом воздействии, а для преобразования операторных схем замещения тех же участков цепей при ненулевых начальных условиях — правила преобразования активных двухполюсников. В частности, последовательная и параллельная схемы замещения емкостного или индуктивного элемента могут быть преобразованы одна в другую с помощью приемов преобразования активных двухполюсников.

Используя операторные схемы замещения идеализированных пассивных элементов, можно получить операторную схему замещения произвольного участка линейной цепи или всей цепи в целом. С этой целью каждый идеализированный пассивный элемент изображенный на схеме замещения цепи для мгновенных значений, должен быть заменен операторной схемой замещения, а токи и напряжения идеализированных источников тока или напряжения — представлены операторными изображениями соответствующих функций. Операторная схема замещения цепи имеет такую же структуру, что и схема замещения цепи для мгновенных значений, но содержит дополнительные независимые источники энергии, определяющие запасы энергии цепи в момент времени, непосредственно предшествовавший коммутации.

Как следует из рассмотренного материала, уравнения электрического равновесия цепи в операторной форме могут быть построены двумя способами: − исходя из уравнений электрического равновесия цепи для мгновенных значений; − непосредственно по операторной схеме замещения цепи, минуя этап формирования уравнений электрического равновесия для мгновенных значений.

Второй способ является менее трудоемким и поэтому он нашел более широкое применение на практике. Метод анализа переходных процессов в линейных цепях, основанный на формировании операторных уравнений электрического равновесия цепей по их операторным схемам замещения, получил название операторного метода анализа переходных процессов. Этот метод представляет собой дальнейшее развитие операторного метода решения дифференциальных уравнений и позволяет анализировать процессы в цепи после коммутации, минуя этап формирования уравнений электрического равновесия цепи для мгновенных значений токов и напряжений.