ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ ТЭи ЕП Лекций

Скачать презентацию ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ ТЭи ЕП Лекций

ТЕОРИЯ ЭКСПЕРИМЕНТА.ppt

Количество слайдов: 192

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Лекций – 32 часа Лабораторных – 16 часов Контрольная работа (расчетная) Зачет (беседа по всему материалу)

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Основная цель любого научного исследования состоит в том, чтобы показать статистическую значимость эффекта воздействия определенного фактора на изучаемую зависимую переменную. Основная цель промышленного эксперимента обычно заключается в извлечении максимального количества объективной информации о влиянии изучаемых факторов на производственный процесс с помощью наименьшего числа дорогостоящих наблюдений

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Обычно любая машина или станок, используемый на производстве, позволяет операторам изменять различные настройки, влияя на качество производимого продукта. Эксперименты позволяют менеджеру, ответственному за производство, улучшать настройки машины, а также выяснить какие факторы вносят наиболее важный вклад в качество продукции. Использование этой информации позволяет улучшить настройки системы, достигнув оптимального качества (технологический аспект).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи В тоже время, менеджера интересует и вопросы затрат. Не любой максимальный по производительности и качеству вариант будет приемлем, т. к. затраты на достижения этого результата могут быть не допустимыми. Отсюда задача – максимизировать технологический критерий при минимизации экономического!

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Использование информации полученной в результате планирования промышленного эксперимента позволяет найти такое технологическое пространство в котором можно реализовать варианты при котором результаты максимальны, при допустимых затратах (минимальных) (экономический аспект).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Кроме того, нам не безразлично какими будут затраты и на проведение самого эксперимента. А эти затраты существенно зависят от того сколько опытов необходимо провести для получения требуемого результата.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Чтобы решить задачу о влиянии, допустим 128 факторов на некоторую оптимизируемую функцию (выход), при стандартном эксперименте потребуется провести минимум: 128 * 128 = 2 097 152 опытов (это при условии, что каждую зависимость мы строим по 3 -м точкам. В тоже время используя планы Плакетта-Бермана мы можем обойтись всего 129 опытами, а затем оценить главный эффект каждого фактора, легко определив, таким образом, какие из факторов важны при изучении процесса.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Планы для смесей. Еще одна проблема, которая достаточно хорошо решается планированием эксперимента – это задачи состав – свойство. Как подобрать такое сочетание компонентов смеси (например, бетона), чтобы его свойства были максимальными, а затраты минимальными?

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Планы для смесей. В работе Корнелла приводится пример типичной задачи анализа смесей. Было проведено исследование для определения оптимального состава рыбного паштета как результата смешения различных пород рыб, идущих на его приготовление (в том числе кефаль, окунь и горбыль). Была получена смесь необходимого питательного состава и отличного вкусового качества при минимальной себестомости

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Планы для смесей. В отличие от обычных экспериментов, в смеси общая сумма долей должна быть постоянна, например, равна 100%. Результаты таких экспериментов обычно представляются графически в виде тернарных графиков.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Основное ограничение этих планов три компоненты в сумме равняются константе (100%) – это выражается в треугольной форме графика. При увеличении количества компонентов возникает пространственная фигура (пирамида 0 и зрительная интерпретация затрудняется.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Планы для смесей с ограничениями. В частности, в планах по изучению смесей на относительные доли компонентов можно наложить дополнительные ограничения (помимо условия постоянства их суммы).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Планы для смесей с ограничениями. Например, предположим, что вы хотите разработать наилучший по вкусу фруктовый пунш, состоящий из смеси пяти фруктовых соков. Поскольку предполагается, что изготовленная смесь должна быть именно фруктовым пуншем, чистые смеси, состоящие только из одного фруктового сока не рассматриваются.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Дополнительные ограничения на область допустимых смесей могут возникнуть из-за высокой стоимости одного из соков или по некоторым другим соображениям, поскольку некоторый конкретный сок не может иметь в смеси долю более чем, скажем, 30% (иначе фруктовый пунш был бы слишком дорог, длительность его хранения была бы невелика, пунш не мог бы производиться в больших количествах и так далее). В этом случае решается совместная задача по двум критериям оптимизации.

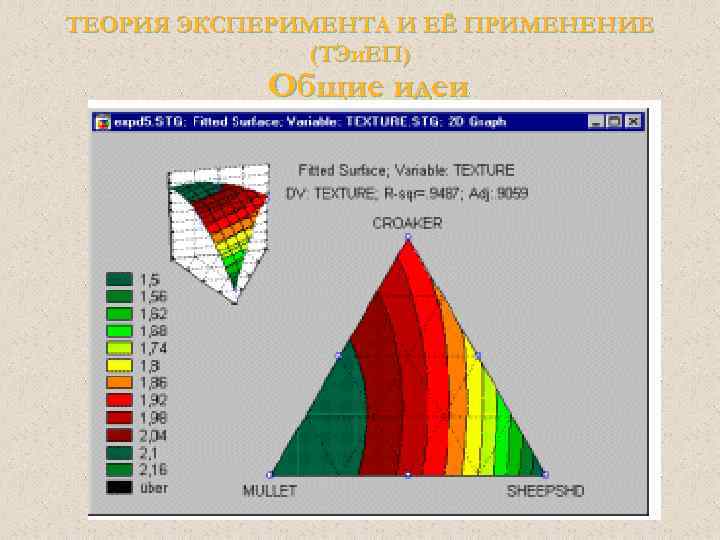
ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи В общем случае, при заданных ограничениях ищется план эксперимента, который позволяет извлечь максимальное количество информации об интересующей нас функции отклика (например, о вкусе фруктового пунша) на выбранной многомерной поверхности.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Вычислительные проблемы: К основным видам задач, решаемых планированием эксперимента , относятся: • планирование оптимального эксперимента • анализ результатов эксперимента. Для решения задач первого вида имеется несколько подходов, реализованных в соответствующих планах экспериментов, основную идею которых можно выразить следующим образом:

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи В общем случае, цель экспериментатора состоит в получении наиболее несмещенной (или наименее смещенной) оценки эффекта фактора вне зависимости от установок других факторов. Более точно, вы пытаетесь построить планы, в которых главные эффекты не смешаны друг с другом, а может быть даже и с взаимодействиями факторов.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Выводы: 1. Экспериментальные методы находят все большее применение в промышленности для оптимизации производственных процессов. 2. Целью этих методов является поиск оптимальных уровней факторов, определяющих течение процесса производства.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Выводы: 3. Многие из этих методов прошли путь от заводских цехов до кабинетов менеджеров и аналитиков, зарекомендовав себя в задачах планирование прибыли в бизнесе, управления финансовыми потоками в банковском деле и многих других (см. , например, работу (1975) Йокиама и Тагучи).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Основные положения классической теории эксперимента: 1. В каждом опыте изменять только один фактор при стабилизации всех остальных (но это ведет к существенному возрастанию количества опытов и сложности интерпретации полученных результатов).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Основные положения классической теории эксперимента: Допустим необходимо найти оптимум для эксперимента в котором критерий оптимизации (отклик – Y) зависит от 3 -х факторов (Х 1, Х 2, Х 3). Каждая кривая может быть построена минимум по 5 точкам. Общее количество опытов составит: 5 * 5 = 125 опытов, А при дублировании – в три раза больше!

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Основная идея ПЭ 2. Построить зависимости критерия оптимизации от одного фактора при стабилизации остальных факторов на определенном (одном из 5 -ти) уровне. В данном примере мы получим 25 зависимостей (графиков). Ниже приведены только 6 кривых из 25.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Y X 2, X 3 = const на min уровне Общие идеи Y Y X 1, X 2 =const на min уровне X 1, X 3, = const на X 1 Y min уровне Y X 2, X 3 = const на среднем уровне X 2 X 3 Y X 1, X 3 = const на X 1, X 2 = const на среднем уровне X 2 X 3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Общие идеи Уже видно, что сделать общий вывод не представляется возможным. Тут то, как говорят и начинается не наука, а искусство, т. е. «колдовство» .

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Основная идея ПЭ Полный факторный эксперимент – ПФЭ 1. Изменять не один фактор, а сразу все. 2. В результате мы должны получить уравнение зависимости критерия оптимизации от исследуемых факторов в виде полинома соответствующей степени (допустим второй степени при 3 -х факторном эксперименте, т. е. с учетом квадратичных зависимостей):

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Основная идея ПЭ (полный факторный эксперимент – ПФЭ) Y = b 0 + b 1 X 1 + b 2 X 2 + b 3 X 3 + + b 12 X 1 X 2 + b 13 X 1 X 3 + b 23 X 2 X 3 + b 123 X 1 X 2 X 3 + + b 11 X 12 + b 22 X 22 + b 33 X 32 Где: Y – критерий оптимизации; Х 1, Х 2, Х 3 – факторы влияющие на результат (критерий оптимизации - Y)

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) МАТРИЦА ПЛАНА ПФЭ Для вычисления коэффициентов математической модели необходимо построить систему с количеством уравнений равным количеству определяемых коэффициентов. Так, для трехфакторной неполной квадратичной модели (без учета квадратичных зависимостей) количество опытов должно быть равно: N = 2 k = 23 = 8 Где k – количество факторов

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) МАТРИЦА ПЛАНА ПФЭ Параметры характеризующие процесс: Y – параметр оптимизации (например, Т - производительность агрегата в соответствующих единицах измерения и Э – себестоимость выпускаемой продукции в единицах измерения; Х – факторы влияющие на параметры оптимизации, например: Х 1 – температура раствора в [o. С] Х 2 – скорость подачи заготовки [км/час] Х 3 – давление в камере [П] и т. д.

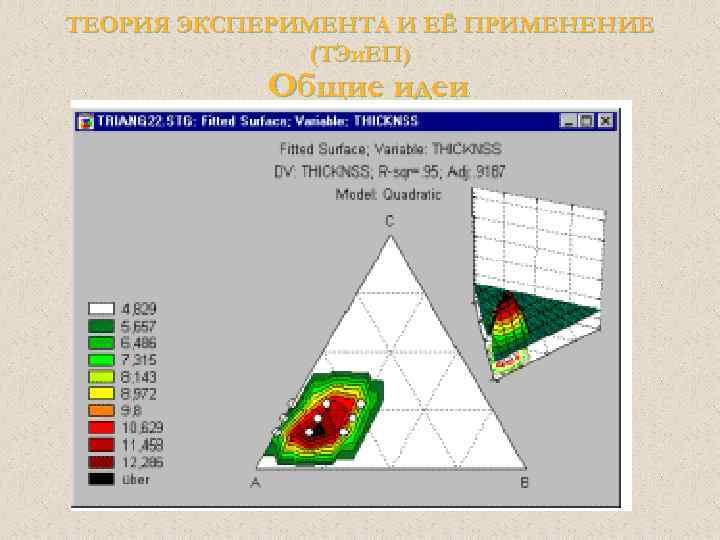
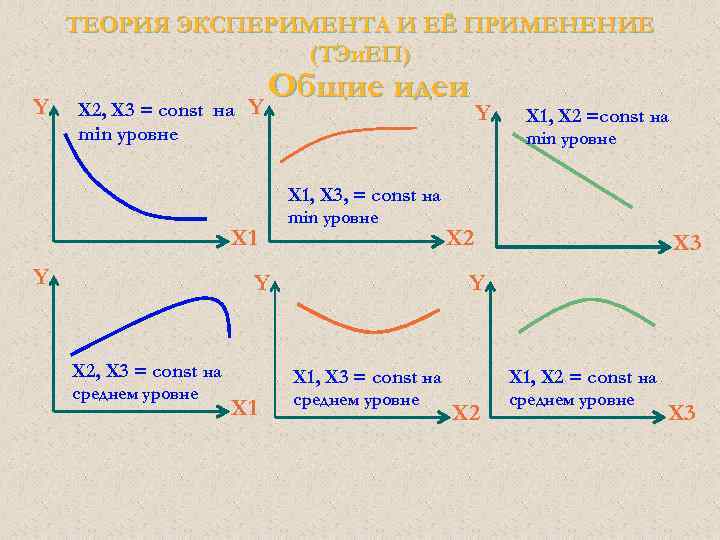
ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) МАТРИЦА ПЛАНА ПФЭ Параметры характеризующие процесс: Выбираем те факторы изменение которых влияет на конечный результат, т. е. на параметры оптимизации (Т. и Э. ) Остальные факторы поддерживаем на определенном, постоянном уровне, рекомендуемом по нормативам или литературным источникам.

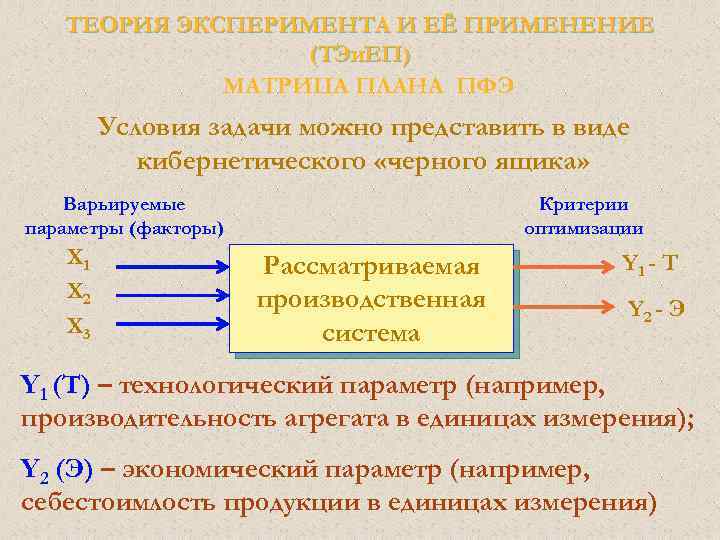ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) МАТРИЦА ПЛАНА ПФЭ Условия задачи можно представить в виде кибернетического «черного ящика» Варьируемые параметры (факторы) Х 1 Х 2 Х 3 Критерии оптимизации Рассматриваемая производственная система Y 1 - Т Y 2 - Э Y 1 (Т) – технологический параметр (например, производительность агрегата в единицах измерения); Y 2 (Э) – экономический параметр (например, себестоимлость продукции в единицах измерения)

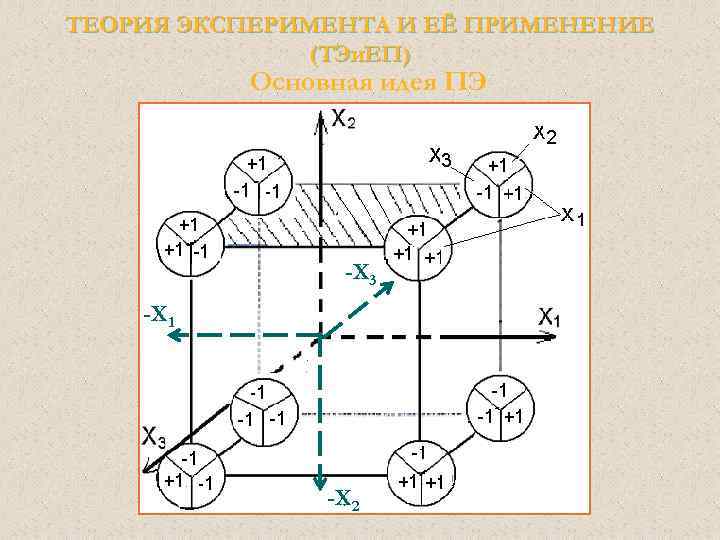
ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) МАТРИЦА ПЛАНА ПФЭ Поскольку геометрически ПФЭ представляет собой куб, то логично пересечение пространственных осей поместить в его центр. Тогда план эксперимента удобно представлять в условных единицах, приняв диапазон изменения каждого параметра от ( -1) до (+1). И необходимо перейти от натуральных единиц измерения факторов к кодированным

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Основная идея ПЭ -Х 3 -Х 1 -Х 2

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Кодирование факторов Формула перехода от физических (натуральных значений факторов – к кодированным имеет вид: Реальный диапазон необходимо представить в нормированных единицах плана. Для примера примем следующие диапазоны изменения факторов:

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Кодирование факторов Допустим имеется технологический процесс, зависящий от трех факторов, ихменяющихся в диапазоне: Х 1 – от 5, 0 до 15, 0 единиц измерения Х 2 – от 16, 0 до 28, 0 единиц измерения Х 3 – от 5, 0 до 25, 0 единиц измерения В эксперименте определяется технорлогический параметр результата Y 1 (Т) – например, производительность и экономический Y 2 (Э) – например себестоимость). Приведем векторное изображение факторов.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Кодирование факторов Векторное изображение фактора (пример) Кодированные значения -1 Натуральные 5, 0 значения Кодированные значения -1 Натуральные значения 16, 0 Кодированные значения -1 Натуральные значения 5, 0 -0, 66 6, 66 -0, 66 18, 0 +0, 33 8, 33 0 10, 0 -0, 33 20, 0 11, 66 13, 33 15, 0 +0, 33 +0, 66 22, 0 -0, 66 -0, 33 8, 33 +0, 66 +1 11, 66 15, 0 24, 0 26, 0 Х 1 +1 Х 2 28, 0 +0, 33 +0, 66 +1 18, 33 21, 66 25, 0 Х 3

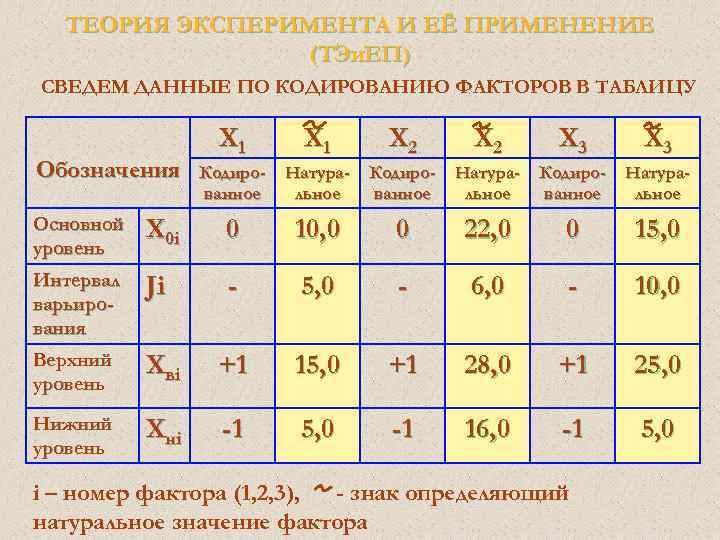ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) СВЕДЕМ ДАННЫЕ ПО КОДИРОВАНИЮ ФАКТОРОВ В ТАБЛИЦУ Обозначения Х 1 Х 2 Х 3 Кодированное Натуральное Основной уровень Х 0 i 0 10, 0 0 22, 0 0 15, 0 Интервал варьирования Ji - 5, 0 - 6, 0 - 10, 0 Верхний уровень Х вi +1 15, 0 +1 28, 0 +1 25, 0 Нижний уровень Х нi -1 5, 0 -1 16, 0 -1 5, 0 i – номер фактора (1, 2, 3), - знак определяющий натуральное значение фактора

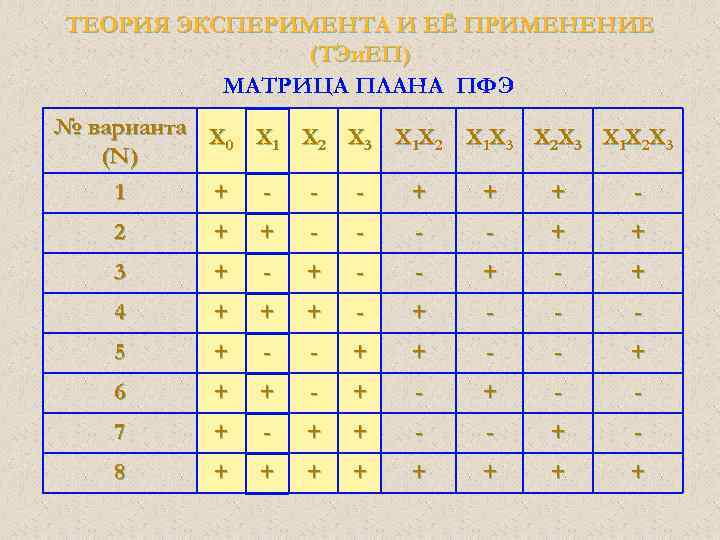ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) МАТРИЦА ПЛАНА ПФЭ № варианта Х Х Х Х 0 1 2 3 1 2 1 3 2 3 1 2 3 (N) 1 + + 2 + + - - + + 3 + - - + 4 + + + - - - 5 + - - + 6 + + - + - - 7 + - + + - - + - 8 + + + +

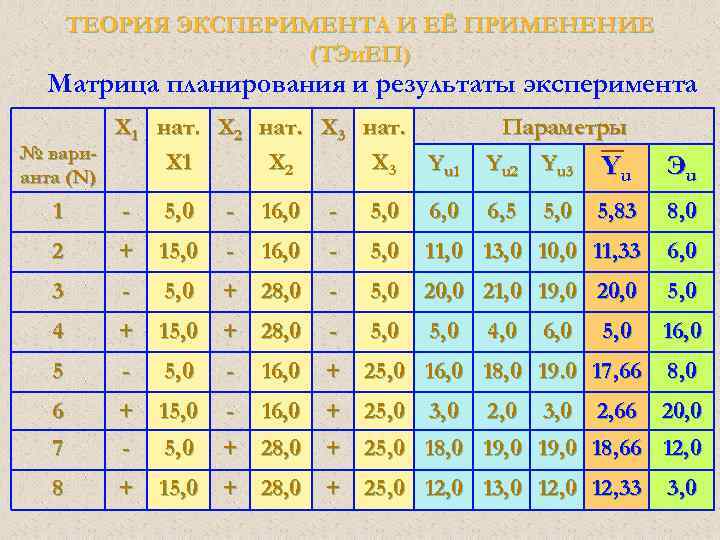ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Матрица планирования и результаты эксперимента Х 1 нат. Х 2 нат. Х 3 нат. № вари. Х 1 Х 2 Х 3 Yu 1 анта (N) Параметры Yu 2 Yu 3 Yu Эu 6, 5 1 - 5, 0 - 16, 0 - 5, 0 6 , 0 5, 83 8, 0 2 + 15, 0 - 16, 0 - 5, 0 11, 0 13, 0 10, 0 11, 33 6, 0 3 - 5, 0 + 28, 0 - 5, 0 20, 0 21, 0 19, 0 20, 0 5, 0 4 + 15, 0 + 28, 0 - 5, 0 16, 0 5 - 5, 0 - 16, 0 + 25, 0 16, 0 18, 0 19. 0 17, 66 8, 0 6 + 15, 0 - 16, 0 + 25, 0 20, 0 7 - 5, 0 + 28, 0 + 25, 0 18, 0 19, 0 18, 66 12, 0 8 + 15, 0 + 28, 0 + 25, 0 12, 0 13, 0 12, 33 3, 0 4, 0 2, 0 5, 0 6, 0 3, 0 5, 0 2, 66 3, 0

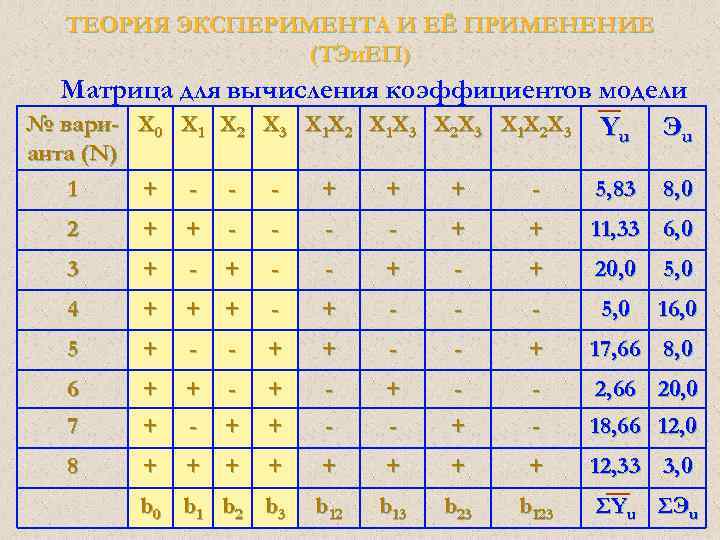ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Матрица для вычисления коэффициентов модели № вари- Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Yu Эu анта (N) 1 + - - - + + + - 5, 83 8, 0 2 + + - - + + 11, 33 6, 0 3 + - - + 20, 0 5, 0 4 + + + - - - 5, 0 16, 0 5 + - - + 17, 66 8, 0 6 + + - + - - 2, 66 20, 0 7 + - + + - - + - 18, 66 12, 0 8 + + + + 12, 33 3, 0 b 1 b 2 b 3 b 12 b 13 b 23 b 123 Σ Yu Σ Эu

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Основная идея 3. Проводить статистическую обработку полученных результатов, для определения возможности использование его для дальнейших исследований: • Для определения равноточности результатов – по критерию Кохрена (G) для соответствующих степеней свободы и заданного уровня значимости (для чего каждый опыт дублируется т. е. проводится в нескольких повторностях (например в тройной k = 3)): Если GЭ < GТ то измерения во всех опытах равноточны и ими можно пользоваться. В противном случае необходимо повторить опыты с наибольшими расхождениями между результатами повторностей, или изменить уровень значимости.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Основная идея 3. Критерий Кохрена (G) рассчитывается по формуле: Где: - среднее арифметическое значение параметра в опыте; Yuj – текущее значение параметра в u-товом опыте и jтовой повторности; Su 2 – построчная дисперсия: где: u – номер опыта в плане u = 1, 2, 3, …, N; N – количество опытов в плане; j – повторность опыта j=1, 2, … φ; φ – количество повторностей опыта, допустим = 3.

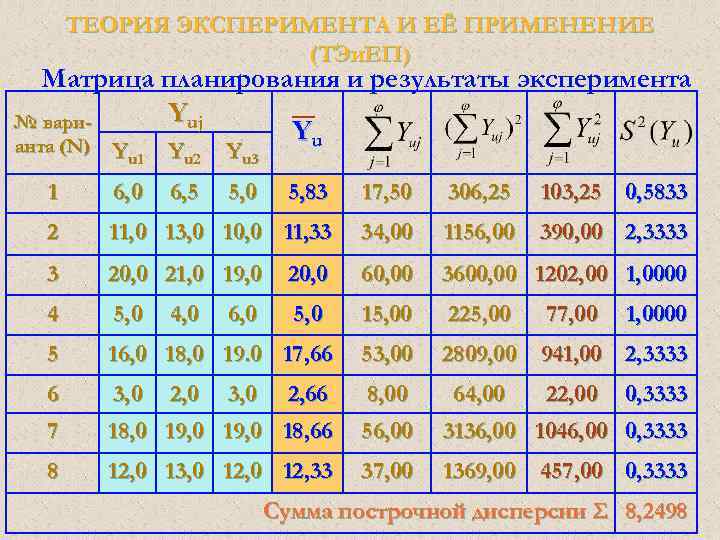ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Матрица планирования и результаты эксперимента Yuj № вари. Yu анта (N) Yu 1 Yu 2 Yu 3 1 6 , 0 6, 5 5, 0 5, 83 17, 50 306, 25 103, 25 0, 5833 2 11, 0 13, 0 10, 0 11, 33 34, 00 1156, 00 390, 00 2, 3333 3 20, 0 21, 0 19, 0 20, 0 60, 00 3600, 00 1202, 00 1, 0000 4 5, 0 15, 00 225, 00 77, 00 5 16, 0 18, 0 19. 0 17, 66 53, 00 2809, 00 941, 00 2, 3333 6 3, 0 2, 66 8, 00 64, 00 7 18, 0 19, 0 18, 66 56, 00 3136, 00 1046, 00 0, 3333 8 12, 0 13, 0 12, 33 37, 00 1369, 00 4, 0 2, 0 6, 0 3, 0 22, 00 1, 0000 0, 3333 457, 00 0, 3333 Сумма построчной дисперсии Σ 8, 2498

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) 3. Проверяем равноточность измерений по критерию Кохрена (G). При α = 0, 05 и f = (φ – 1 )= 3 -1=2 GT = 0, 5157 Следовательно, т. к. GЭ = 0, 2828 < GТ = 0, 5157, то заключаем, что измерения во всех вариантах (опытах) равнозначны.

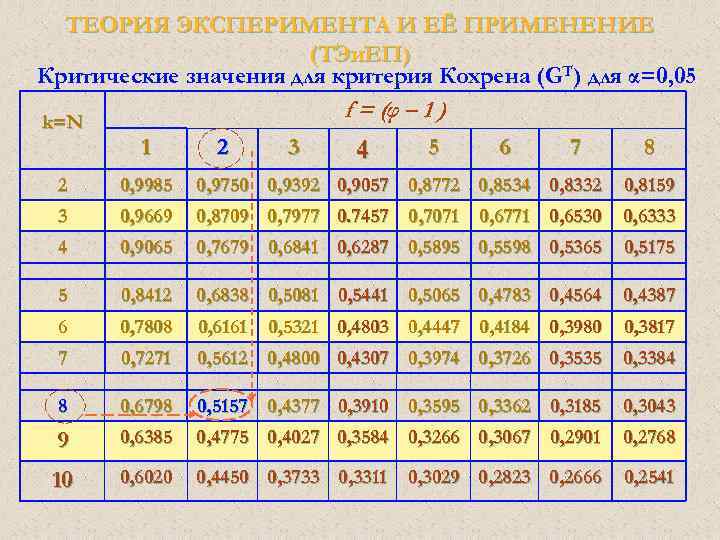ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Критические значения для критерия Кохрена (GT) для α=0, 05 k=N f = (φ – 1 ) 1 2 3 4 5 6 7 8 2 0, 9985 0, 9750 0, 9392 0, 9057 0, 8772 0, 8534 0, 8332 0, 8159 3 0, 9669 0, 8709 0, 7977 0. 7457 0, 7071 0, 6771 0, 6530 0, 6333 4 0, 9065 0, 7679 0, 6841 0, 6287 0, 5895 0, 5598 0, 5365 0, 5175 5 0, 8412 0, 6838 0, 5081 0, 5441 0, 5065 0, 4783 0, 4564 0, 4387 6 0, 7808 0, 6161 0, 5321 0, 4803 0, 4447 0, 4184 0, 3980 0, 3817 7 0, 7271 0, 5612 0, 4800 0, 4307 0, 3974 0, 3726 0, 3535 0, 3384 8 0, 6798 0, 5157 0, 4377 0, 3910 0, 3595 0, 3362 0, 3185 0, 3043 9 0, 6385 0, 4775 0, 4027 0, 3584 0, 3266 0, 3067 0, 2901 0, 2768 10 0, 6020 0, 4450 0, 3733 0, 3311 0, 3029 0, 2823 0, 2666 0, 2541

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Дисперсионный анализ • Определяется дисперсия параметра оптимизации (дисперсия воспроизводимости эксперимента): Определяем ошибку эксперимента:

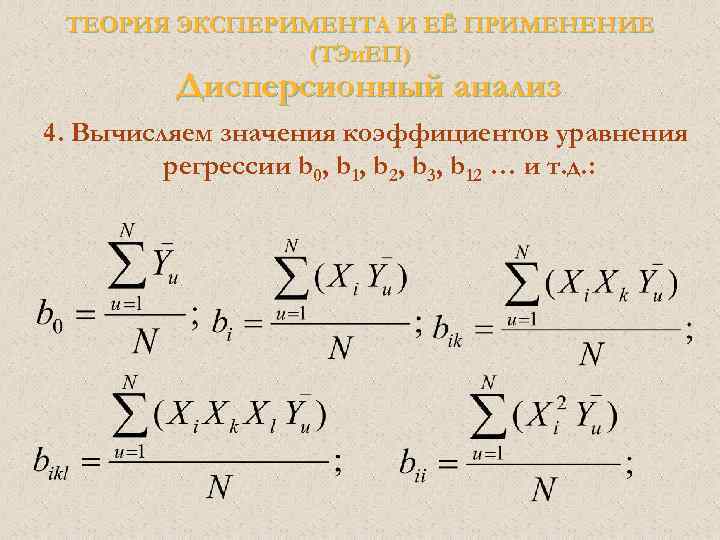ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Дисперсионный анализ 4. Вычисляем значения коэффициентов уравнения регрессии b 0, b 1, b 2, b 3, b 12 … и т. д. :

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Дисперсионный анализ 4. Вычисляем значения коэффициентов уравнения регрессии (для примера) и т. д.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Дисперсионный анализ 4. Вычисляем значения коэффициентов уравнения регрессии (для примера) b 0 = 11, 68; b 23 = 0, 35; b 1 = -3, 85; b 123 = 3, 64; b 2 = 2, 31; b 3 = 1, 14; b 12 = -1, 47; b 13 = -1, 47;

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Дисперсионный анализ 4. Вычисляем значения коэффициентов уравнения регрессии (для примера) Y = b 0 + b 1 X 1 + b 2 X 2 + b 3 X 3 + + b 12 X 1 X 2 + b 13 X 1 X 3 + b 23 X 2 X 3 + b 123 X 1 X 2 X 3 Y = 11, 68 – 3, 85 Х 1 + 2, 31 X 2 + 1, 14 X 3 -1, 47 X 1 X 2 - 1, 47 X 1 X 3 + 0, 35 X 2 X 3 + + 3, 64 X 1 X 2 X 3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Дисперсионный анализ Проверим правильность подсчета коэффициентов. Для примера проверим вариант № 3 (Х 1 = -1; Х 2 = +1; Х 3 = -1; Y = 20, 00) Y = 11, 68 – 3, 85(-1) + 2, 31(+1) + 1, 14(-1) -1, 47(-1)(+1) - 1, 47(-1) + 0, 35(+1)(-1) + +3, 64(-1)(+1)(-1) = 11, 68+3, 85+2, 31 - 1, 14+1, 47 -0, 35+3, 64 = 20, 00

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ 5. Проводится регрессионный анализ полученной математической (регрессионной) модели, включающей: • Определение ошибки при вычислении коэффициентов модели, для ортогональных планов по формуле:

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ 5. Для примера, определение ошибки при вычислении коэффициентов модели, для ортогональных планов по формуле (ошибки всех коэффициентов равны):

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ • Проверяем значимость коэффициентов модели: Где: t –критерий Стьюдента, определяемый по таблице при заданном уровне значимости α = 0, 05 (или 0, 01) и при числе степеней свободы f = N(φ-1).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Критические значения для критерия Стьюдента (t) f = N(φ – 1) α 0, 10 0, 05 0, 025 8 1, 8595 2, 3060 2, 7515 9 1, 6331 2, 2622 2, 6850 10 1, 8125 2, 2281 2, 6383 11 1, 7959 2, 2010 2, 5931 12 1, 7823 2, 1788 2, 5600 13 1, 7709 2, 1604 2, 5326 14 1, 7613 2, 1448 2, 5096 15 1, 7530 2, 1315 2, 4899 16 1, 7459 2, 1199 2, 4729

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Проверяем значимость коэффициентов модели: Где: t –критерий Стьюдента, определяемый по таблице при заданном уровне значимости α = 0, 05 и при числе степеней свободы f = N(φ-1)=16, равен 2, 1199 Наименьший по коэффициент /b 23/ = 0, 35 > 0, 3105 Все коэффициенты математической модели ЗНАЧИМЫ

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ • Проверяем адекватность математической модели: • Вычисляется дисперсия неадекватности (остаточная дисперсия) по формуле: Где: - значение отклика, вычисленное по уравнению (со значимыми членами) в u–ом варианте; k • - число значимых коэффициентов уравнения включая b 0.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Если все коэффициенты модели оказались значимыми, то следует исключить из модели коэффициент имеющий самое малое значение и высчитать адекватность модели без него, если без него модель окажется адекватной, то с ним тем более. Удалим из уравнения /b 23/ = 0, 35? И рассчитываем построчные дисперсии неадекватности:

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Матрица для вычисления дисперсии неадекватности № варианта (N) Yu 1 2 3 4 5 6 7 8 5, 83 11, 33 20, 0 5, 0 17, 66 2, 66 18, 66 12, 33 Расчетное значение Yu 11, 68+3, 85 -2, 31 -1, 14 -1, 47 -3, 64 = Yu (Yu-Yu)2 5, 50 0, 33 0, 1089 11, 68 -3, 85 -2, 31 -1, 14+1, 47+3, 64 = 10, 96 0, 37 0, 1369 11, 68+3, 85+2, 31 -1, 14+1, 47 -1, 47+3, 64= 20, 34 -0, 34 0, 1156 5, 36 -0, 36 0, 1296 11, 68+3, 85 -2, 31+1, 14 -1, 47+3, 64= 18, 00 -0, 34 0, 1156 3, 02 -0, 36 0, 1296 11, 68+3, 85+2, 31+1, 14+1, 47 -3, 64 = 18, 26 0, 38 0, 1244 0, 35 0, 1225 Σ 1, 0031 11, 68 -3, 85+2, 31 -1, 14 -1, 47+1, 47 -3, 64 = 11, 68 -3, 85 -2, 31+1, 14+1, 47 -3, 64 = 11, 68 -3, 85+2, 31+1, 14 -1, 47+3, 64 = 11, 96

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Рассчитываем дисперсию неадекватности:

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Если все коэффициенты модели оказались значимыми, то следует исключить из модели коэффициент имеющий самое малое значение и высчитать адекватность модели без него, если без него модель окажется адекватной, то с ним тем более. • Вычисляем экспериментальное значение коэффициента Фишера по следующей формуле.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Критические значения для критерия Фишера (F T) для α=0, 05 f 2 = N(φ – 1) f 1 = N-k • 1 2 3 8 5, 318 4, 459 4, 066 9 5, 117 4, 257 3, 863 10 4, 965 4, 103 3, 708 11 4, 844 3, 962 3, 587 12 4, 747 3, 885 3, 490 13 4, 667 3, 605 3, 411 14 4, 600 3, 739 3, 344 15 4, 543 3, 682 3, 287 16 4, 494 3, 634 3, 239

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Экспериментальный FЭ – критерий Фишера: Находим из таблицы критическое значение распределения F при уровне значимости α = 0, 05 (или 0, 01) и при числе степеней свободы f 1 = N - k • ; и f 2 = N(φ-1). Если FЭ ≤ FТ при заданных f 1 и f 2 , то уравнение считается адекватным действительному процессу. В противном случае – неадекватно.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Критическое (табличное) значение FT – критерий Фишера для примера: Находим из таблицы критическое значение распределения F при уровне значимости α = 0, 05 и при числе степеней свободы f 1 = N - k • = 8 -7 =1; и f 2 = N(φ-1) = 8(3 -1) = 16. FT = 4, 494

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Экспериментальный FЭ – критерий Фишера для приме Поскольку, FЭ = 5, 8365 > FТ =4, 494. то с доверительным интервалом Р= 1 -α = 1 -0, 05 = 0, 95 математическую модель можно считать неадекватной. Это и понятно, т. к. мы удалили значимый коэффициент b 23 = 0, 35. Следовательно с этим коэффициентом математическая модель будут адекватной рассматриваемому процессу.

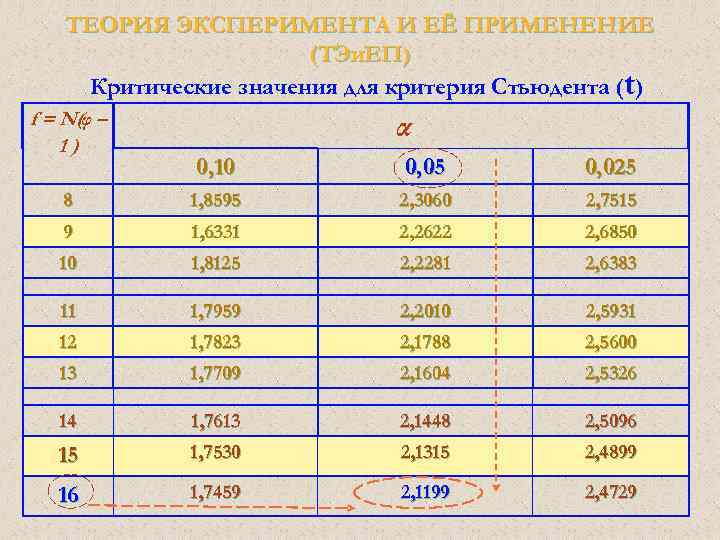
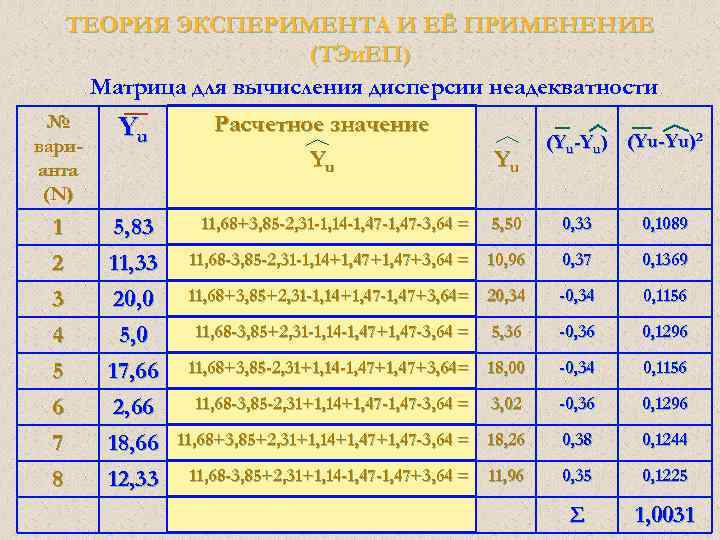
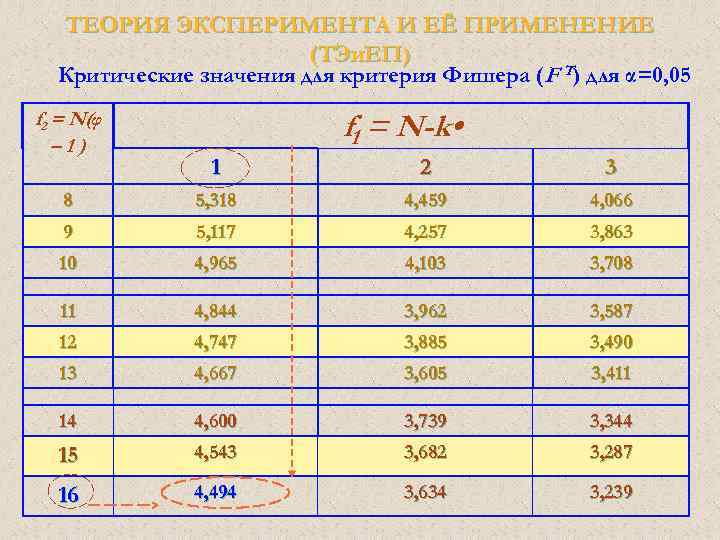
ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Математическая модель как интерполяционная формула Областью ПФЭ типа 23 есть трёхмерный куб. Опытные точки (варианты) расположены в вершинах куба с координатами + 1 или -1

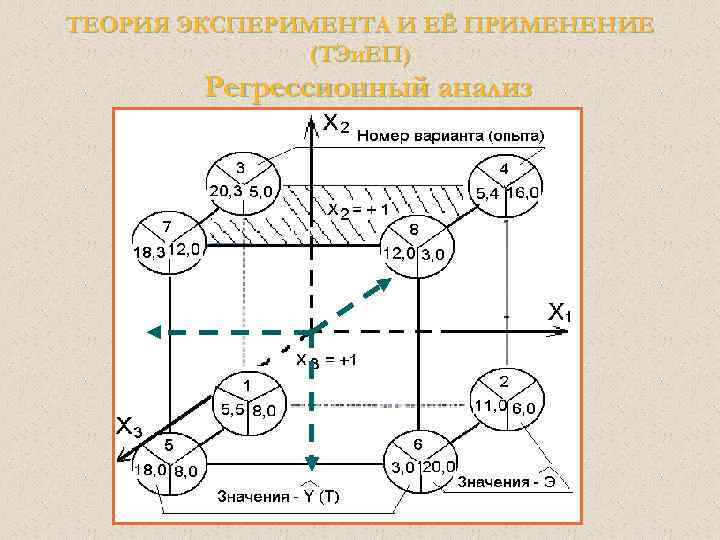ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ

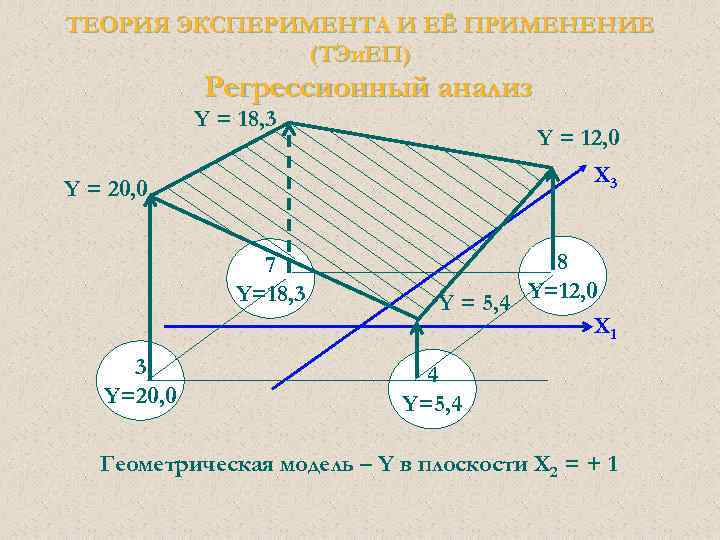ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Y = 18, 3 Y = 12, 0 Х 3 Y = 20, 0 7 Y=18, 3 3 Y=20, 0 8 Y=12, 0 Y = 5, 4 Х 1 4 Y=5, 4 Геометрическая модель – Y в плоскости Х 2 = + 1

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Y = 11, 68 – 3, 85 Х 1 + 2, 31 X 2 + 1, 14 X 3 - 1, 47 X 1 X 2 - 1, 47 X 1 X 3 + 0, 35 X 2 X 3 + 3, 64 X 1 X 2 X 3 Изокванты технического параметра – Y на плоскости Х 2 = + 1 (28, 0) Y = 13, 99 – 5, 32 Х 1 + 1, 49 X 3 + 2, 17 X 1 X 3 для Х 1 = +1: Y = 8, 67 + 3, 66 Х 3 для Х 1 = - 1: Y = 19, 31 - 0, 68 X 3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Дисперсионный анализ для Х 1 = + 1: № Х 3 1 -1 2 Y = 8, 67 + 3, 66 X 3 Y 8, 67 – 3, 66 = 5, 01 - 0, 66 8, 67 - 2, 42 = 6, 25 3 - 0, 33 8, 67 - 1, 21 = 7, 46 4 0 8, 67 + 0 = 8, 67 5 + 0, 33 8, 67 + 1, 21 = 9, 88 6 + 0, 66 8, 67 + 2, 42 = 11, 09 7 +1 8, 67 + 3, 66 = 12, 33

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Дисперсионный анализ Y = 19, 31 – 0, 68 X 3 № Х 1 Х 3 Y 19, 31 + 0, 68 = 19, 99 1 - - 2 - - 0, 66 19, 31 + 0, 68*0, 66 = 19, 76 3 - - 0, 33 19, 31 + 0, 68*0, 33 = 19, 53 4 - 0 5 - + 0, 33 19, 31 - 0, 68*0, 33 = 19, 08 6 - + 0, 66 19, 31 - 0, 68*0, 66 = 18, 86 7 - + 19, 31 + 0, 00 = 19, 31 – 0, 68 = 18, 63

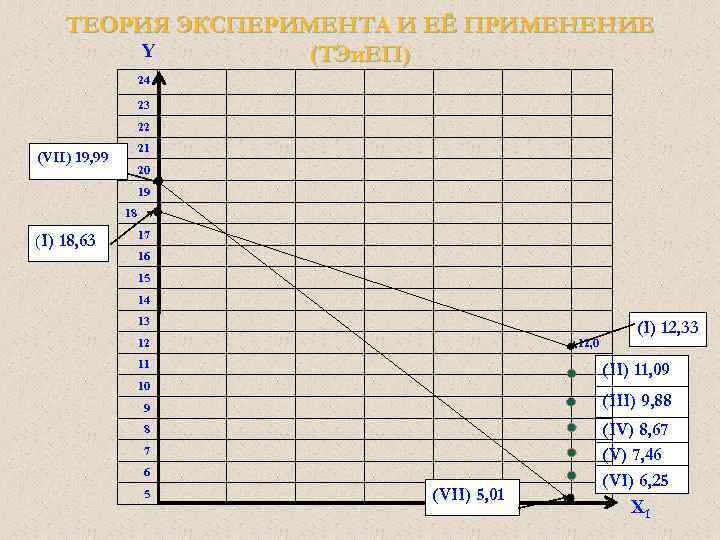ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Y (ТЭи. ЕП) 24 23 22 21 (VII) 19, 99 20 19 18 (I) 18, 63 17 16 15 14 13 12 12, 0 11 (II) 11, 09 10 (III) 9, 88 9 8 7 6 5 (I) 12, 33 (VII) 5, 01 (IV) 8, 67 (V) 7, 46 (VI) 6, 25 Х 1

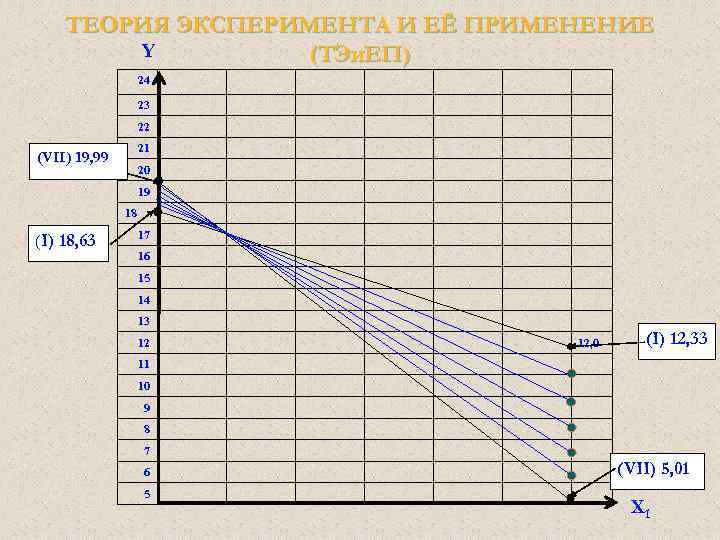ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Y (ТЭи. ЕП) 24 23 22 21 (VII) 19, 99 20 19 18 (I) 18, 63 17 16 15 14 13 12 12, 0 (I) 12, 33 11 10 9 8 7 6 5 (VII) 5, 01 Х 1

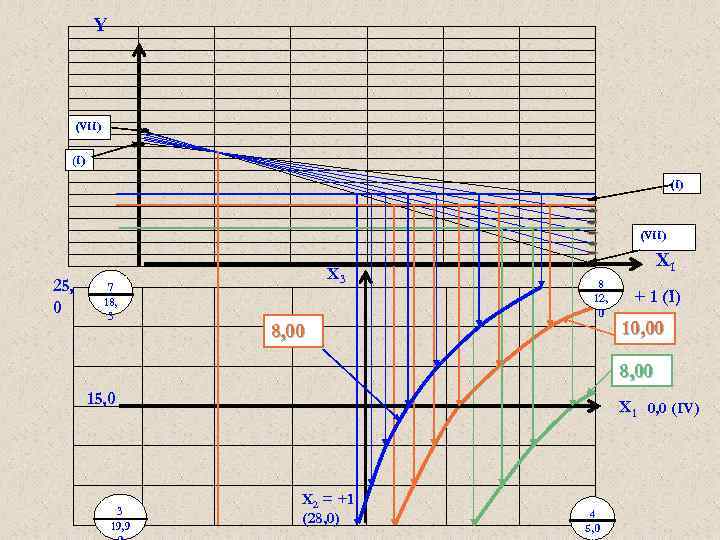Y (VII) (I) (VII) 25, 0 7 18, 3 X 3 Х 1 8 12, 0 8, 00 + 1 (I) 10, 00 8, 00 15, 0 3 19, 9 X 1 0, 0 (IV) Х 2 = +1 (28, 0) 4 5, 0

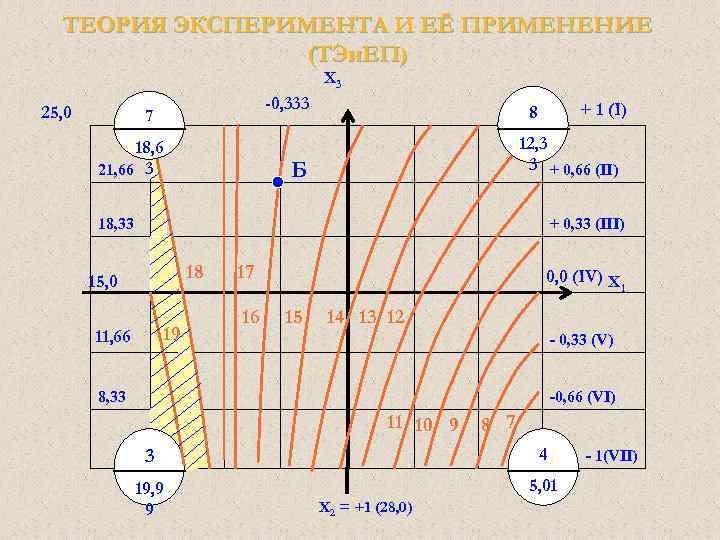ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) X 3 25, 0 -0, 333 7 18, 6 21, 66 3 + 1 (I) 8 12, 3 3 + 0, 66 (II) Б 18, 33 + 0, 33 (III) 18 15, 0 19 11, 66 17 16 0, 0 (IV) X 15 1 14 13 12 - 0, 33 (V) 8, 33 -0, 66 (VI) 11 10 9 4 - 1(VII) 3 19, 9 9 8 7 5, 01 Х 2 = +1 (28, 0)

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Проверка правильности начертания изоквант Проверка производится в произвольно выбранной точке, например в точке «Б» (для Т) с координатами Х 1 = -0, 333; Х 2 = +1; Х 3 = + 0, 666. Подставим эти координаты в полученную математическую модель – Y, мы должны получить результат близкий к « 16» : YБ = 11, 68 – 3, 85*(-0, 333) + 2, 31(+1) + 1, 14(+0, 666) 1, 47(-0, 333*(+1)) - 1, 47(-0, 333*0, 666) + 0, 35(+1*0, 666) + 3, 64(-0, 333*(+1)*0, 666) = 11, 68 + 1, 282 + 2, 31 + 0, 759+ + 0, 49 + 0, 326 + 0, 233 - 0, 807 = 16, 273 ≈ 16

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Изокванты экономического параметра на плоскости Х 2 = +1(28, 0) Э = 9, 70 + 1, 50 Х 1 – 0, 75 Х 2 + 1, 00 Х 3 – -1, 00 Х 1 Х 2 – 0, 75 Х 1 Х 3 – 2, 50 Х 2 Х 3 – -4, 25 Х 1 Х 2 Х 3

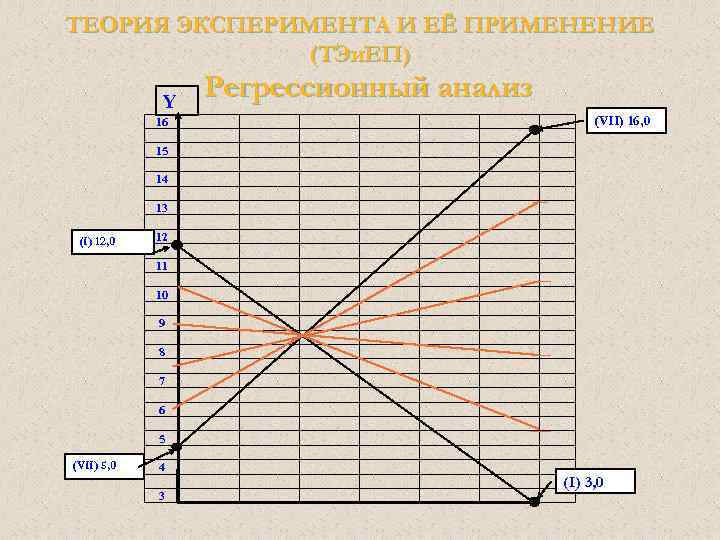ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Y 16 Регрессионный анализ (VII) 16, 0 15 14 13 (I) 12, 0 12 11 10 9 8 7 6 5 (VII) 5, 0 4 3 (I) 3, 0

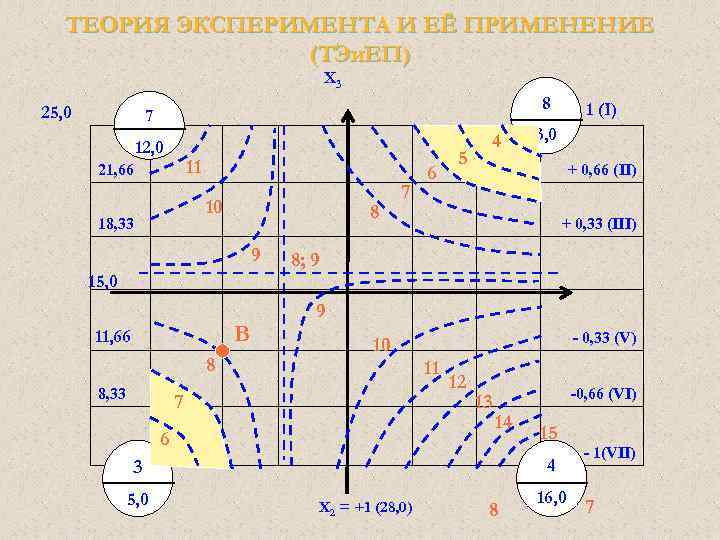ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) X 3 25, 0 8 7 12, 0 11 21, 66 10 18, 33 8 9 15, 0 В 11, 66 8 8, 33 7 6 5 4 3, 0 + 0, 66 (II) + 0, 33 (III) 8; 9 9 - 0, 33 (V) 10 11 7 6 12 13 -0, 66 (VI) 14 15 - 1(VII) 4 3 5, 0 + 1 (I) Х 2 = +1 (28, 0) 8 16, 0 7

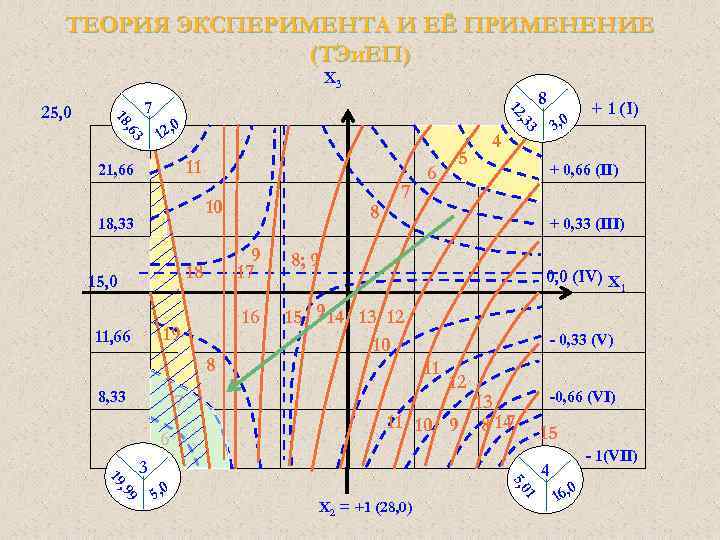ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) X 3 , 63 0 12, 11 21, 66 10 18, 33 8 8, 33 7 6 + 0, 66 (II) 8; 9 16 19 11, 66 5 15 9 14 13 12 10 0, 0 (IV) X 11 12 -0, 66 (VI) 13 11 10 9 8 14 7 15 1 5, 0 , 99 19 Х 2 = +1 (28, 0) 1 - 0, 33 (V) 3 5, 0 + 1 (I) 3, 0 + 0, 33 (III) 9 17 18 15, 0 8 7 6 4 8 , 33 12 7 18 25, 0 4 - 1(VII) 0 16,

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Проверка правильности начертания изоквант Проверка производится в произвольно выбранной точке, например в точке «В» (для Э) с координатами Х 1 = -0, 666; Х 2 = +1; Х 3 = - 0, 333. Подставим эти координаты в полученную математическую модель – Э, мы должны получить результат близкий к « 8» : ЭВ = 9, 70 + 1, 50(-0, 666) – 0, 75(+1) + 1, 00(-0, 333) – -1, 00(-0, 666*(+1)) – 0, 75(-0, 666)(-0, 333)– 2, 50(+1)(-0, 333) – 4, 25(-0, 666((+1)(-0, 333) = 8, 012 ≈ 8

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Если условия позволяют, то желательно провести прогноз значений Y и Э за пределами выбранного нами факторного пространства, а именно, хотя бы в точке «С» с координатами Х 1 = -1, 5; Х 2 - + 1; Х 3 = - 1, 2. YС = 11, 68 – 3, 85*(-1, 5) + 2, 31(+1) + 1, 14(-1, 2) - 1, 47(1, 5*(+1)) - 1, 47(-1, 5*-1, 2) + 0, 35(+1*-1, 2) + 3, 64(1, 5*(+1)*-1, 2) = 11, 68 + 1, 282 + 2, 31 + 0, 759+0, 49 + 0, 326 + 0, 233 - 0, 807 = 24, 09 > 20, 0

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ ЭС = 9, 70 + 1, 50(-1, 5) – 0, 75(+1) + 1, 00(-1, 2) – -1, 00(-1, 5*(+1)) – 0, 75(-1, 5)(-1, 2)– 2, 50(+1)(-1, 2) – 4, 25(1, 258*(+1)(-1, 2) = 4, 0 < 5 Результаты расчетов Y и Э показывают, что направление выбранное нами правильное. Поэтому для улучшения показателей Y и Э необходимо сдвинуть факторное пространство в направлении указанном стрелкой на совместном для Y и Э графике.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Нахождение оптимального решения. 1. В область совместного решения вписываем окружность максимального радиуса; 2. В окружность вписываем квадрат со сторонами параллельными исходному; 3. Определяем общий центр квадрата и окружности; 4. Выносим координаты центра на координатные оси; 5. Находим оптимальное решение и максимальные возможные отклонения по осям – дельту.

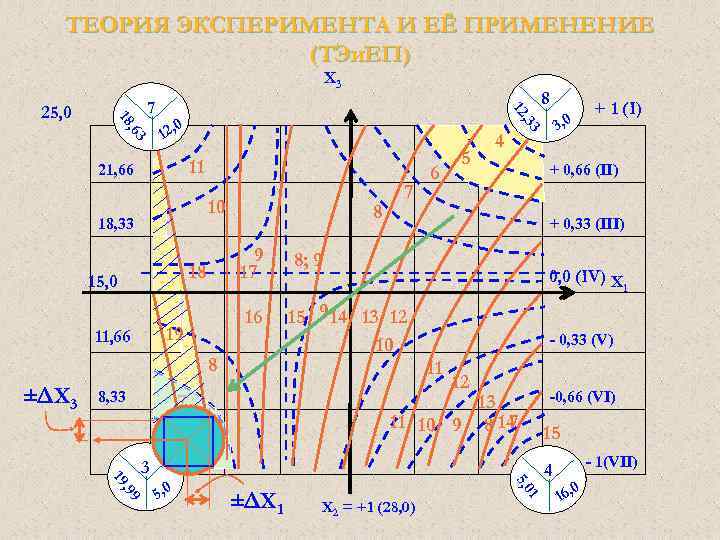ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) X 3 , 63 0 12, 11 21, 66 10 18, 33 15 9 14 13 12 10 8 ±ΔХ 3 8, 33 + 0, 66 (II) 8; 9 16 19 11, 66 5 0, 0 (IV) X 12 -0, 66 (VI) 13 11 10 9 8 14 7 6 1 - 0, 33 (V) 11 7 + 1 (I) 3, 0 + 0, 33 (III) 9 17 18 15, 0 8 7 6 4 8 , 33 12 7 18 25, 0 15 - 1(VII) ±ΔХ 1 Х 2 = +1 (28, 0) 1 5, 0 , 99 19 3 4 0 16,

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Регрессионный анализ Нахождение оптимального решения. 1. Х 1 = - 0, 832 ± 0, 117 или 5, 84 н. ед. ± 0, 585 н. ед. 2. Х 2 = +1 – (28, 0 натуральных единиц); 3. Х 3 = - 0, 832 ± 0, 117 или 6, 68 н. ед. ± 1, 17 н. ед.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ДРОБНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ – N = 2 k-p При линейной зависимости поверхности отклика от факторов тройные и парные взаимодействия могут быть незначимыми, то можно увеличить количество изменяемых в эксперименте факторов. Для этого поступают следующим образом – заменяют заведомо незначимое (малозначимое) взаимодействие новым фактором, например, Х 4.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ДФЭ – N = 2 k-g Тогда уравнение регрессии (например, для полуреплики ДФЭ: N=2 7 -4) будет выглядеть следующим образом: Y = b 0+b 1 X 1+b 2 X 2+b 3 X 3+b 4 X 4+b 5 X 5+b 6 X 6+b 7 X 7 План в приведенной выше таблице описывается как 2 (7 -4) план разрешения (три). Это означает, что III изучается k = 7 факторов (первая цифра в скобках), однако p = 4 из этих факторов (вторая цифра в скобках) порождены взаимодействиями полного факторного плана 2 [(11 -7) = 4].

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ДФЭ – N = 2 k-g В результате план не обеспечивает полного разрешения имеются эффекты взаимодействий, , т. е. которые смешиваются с другими эффектами (идентичны им). Главные эффекты в этом плане смешиваются со взаимодействиями 2 -го порядка и, следовательно, все взаимодействия более высоких порядков также смешаны.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Если необходимо просеять большое число факторов, которые могут быть потенциально важными (т. е. связаны с интересующей нас зависимой переменной), хотелось бы использовать план, который бы позволил тестировать наибольшее число главных эффектов при наименьшем числе наблюдений, то есть построить план разрешения III с наименьшим числом наблюдений.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Один из способов планирования такого эксперимента состоит в смешивании всех взаимодействий с “новыми” главными эффектами. Такие планы часто называют насыщенными , поскольку вся информация в них используется для оценки параметров, не оставляя степеней свободы для оценки эффекта (члена) ошибок ДА.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Поскольку дополнительные факторы создаются приравниванием (“присвоением псевдонимов”) “новых факторов” к взаимодействиям в полной факторной модели, то эти планы всегда будут состоять из 2 k опытов, (то есть, 4, 8, 16, 32 и так далее опытов). Плакетт и Берман (Plackett и Burman, 1946) показали, как полная факторная модель может быть разбита так, чтобы получить насыщенные планы, в которых число опытов кратно 4, а не степени 2. Такие планы иногда называют планами с матрицей Адамара.

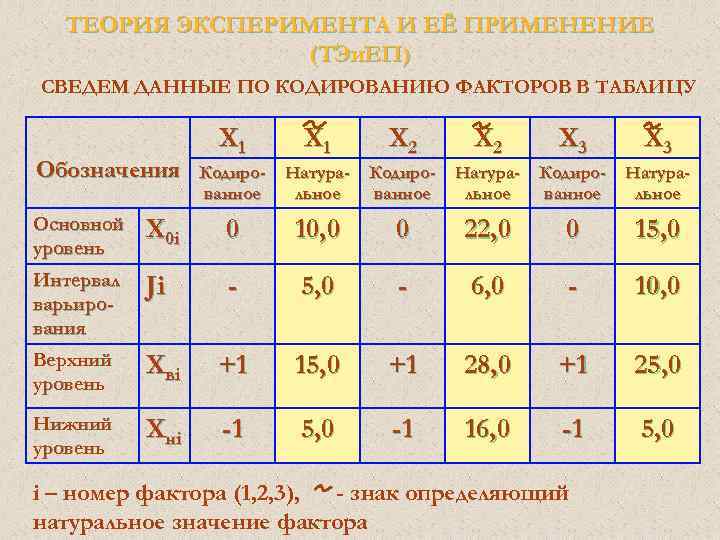ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Усиление разрешения плана методом инверсии Одним из способов, с помощью которых разрешение III плана может быть усилено до разрешения IV, является метод инверсии (например, смотрите Box и Draper, 1987, Deming и Morgan, 1993). Предположим, что имеется 7 - факторный план с 8 опытами:

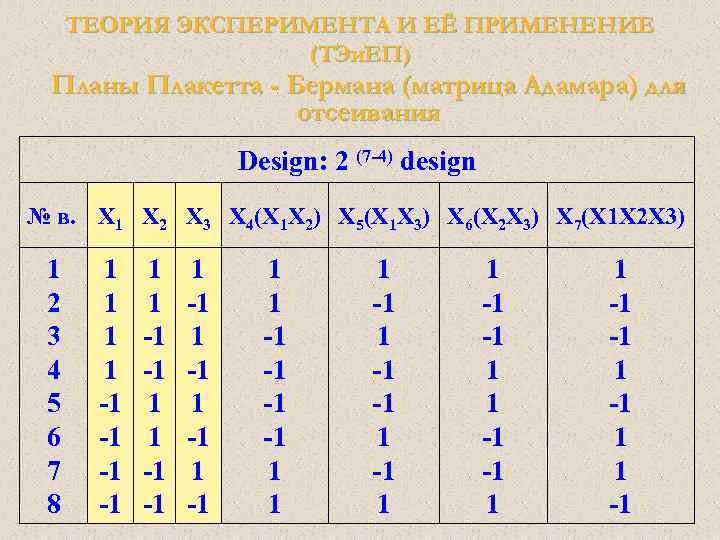ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Design: 2 (7 -4) design № в. Х 1 Х 2 Х 3 Х 4(X 1 X 2) Х 5(X 1 X 3) Х 6(X 2 X 3) Х 7(X 1 X 2 X 3) 1 2 3 4 5 6 7 8 1 1 -1 -1 1 -1 1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Это план с разрешением III, в нем 2 -х факторные взаимодействия смешаны с главными эффектами. Вы можете преобразовать его в план разрешения IV с помощью опции Инверсия (усиление разрешен. При инверсии весь план копируется и добавляется в конец исходного плана с обращением всех знаков (заменой на противоположные):

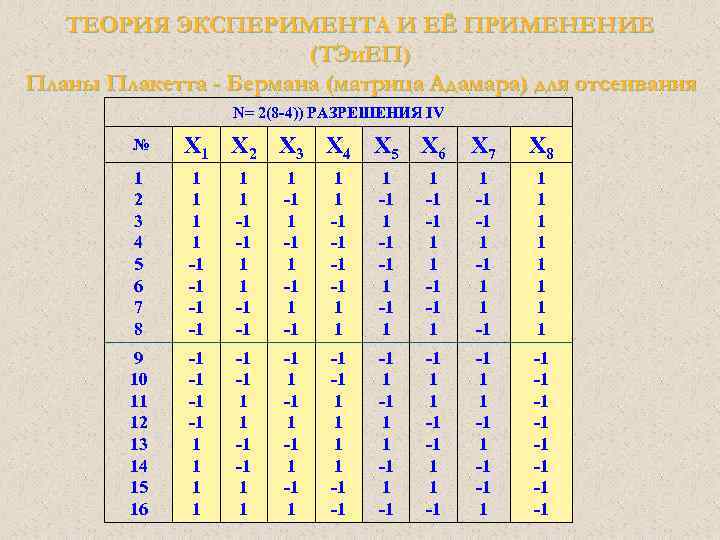ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания N= 2(8 -4)) РАЗРЕШЕНИЯ IV Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 1 2 3 4 5 6 7 8 1 1 -1 -1 1 -1 1 -1 1 1 -1 -1 1 1 -1 -1 1 1 1 1 9 10 11 12 13 14 15 16 -1 -1 1 1 -1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 -1 -1 №

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Подводя итоги, заметим, что коль скоро вы хотели бы включить меньше наблюдений (опытов) в ваш эксперимент, чем это требуется полным факторным планом 2 k, вы “жертвуете” эффектами взаимодействия и приписываете их некоторым уровням факторов. Получающийся план не является больше полным факторным, а становится дробным факторным.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Фундаментальное тождество. Другой способ описания генератора плана состоит в простом уравнении. Именно, если, например, фактор 5 в дробном факторном плане идентичен взаимодействию 123 (фактор 1 и фактор 2 и фактор 3), тогда, умножая кодированные значения взаимодействия 123 на кодированные значения фактора 5, мы получим в результате +1 (если все уровни факторов закодированы +1 ) или: I = 1235

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания где символ I заменяет +1 (используя стандартные обозначения как, например, в Box и Draper, 1987). Так, мы знаем, что фактор 1 смешан с взаимодействием 235 , фактор 2 смешан с взаимодействием 13 5 , а фактор 3 смешан с взаимодействием 125 , поскольку в каждом случае их произведение должно равняться 1. Смешанность взаимодействий 2 -го порядка также определяется этим уравнением, поскольку взаимодействие 12 , будучи умножено на взаимодействие 35 , должно дать в результате 1 и, следовательно, они идентичны или смешаны.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Поэтому можно суммировать все смешанные в плане эффекты с помощью подобного тождества, называемого фундаментальным тождеством.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Рандомизация опытов. Поскольку многие условия проведения эксперимента могут измениться от опыта к опыту то, чтобы не возникали систематические смещения, следует рандомизировать порядок проведения опытов (случайно выбрать порядок их проведения).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Добавление центральных точек (центроидов) Планирование эксперимента для факторов, установленных на двух уровнях неявно предполагает, что их воздействие на зависимую переменную (например, на прочность ткани) линейно. При этом невозможно проверить, имеется ли нелинейная компонента (например, квадратичная) в соотношении между фактором X и зависимой переменной, коль скоро X оценивается только в двух точках (например, нижнем верхнем и уровнях).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Если предполагается, что соотношение между факторами и зависимой переменной, скорее всего, нелинейно, то необходим один или несколько опытов, где все (непрерывные) факторы установлены в промежуточных (средних) точках. Такие опыты принято называть опытами в центральных точках (или просто в центрах), поскольку они в некотором смысле находятся в центре плана (смотрите график).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Позднее при анализе (смотрите ниже) можно сравнить измерения зависимой переменной в центральной точке со средним в остальных точках плана. Это дает возможность проверить нелинейность зависимостей (смотрите Box и Draper, 1987): Если среднее зависимой переменной в центре плана значительно отличается от общего среднего по всем остальным точкам плана, то это является основанием считать, что простое предположение о линейности связи факторов с зависимой переменной не выполняется.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Выводы Планы 2(k-p) наиболее часто используются в промышленности. Вклад большого числа факторов в производственный процесс может быть оценен относительно эффективно (т. е. с помощью небольшого числа опытов). Логика экспериментов такого рода весьма проста (каждый фактор имеет только два уровня)/

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Недостатки. Простота этих планов является их главным недостатком. Как было отмечено ранее, основанием для использования двухуровневых факторов является убеждение в том, что изменения зависимой переменной (например, прочности ткани) линейны своей природе. Часто по это не выполняется, то есть многие переменные связаны с характеристиками качества нелинейным образом.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Недостатки. Трудно обнаружить в насыщенных планах нелинейность. Нелинейность может быть обнаружена, если план содержит центральную точку. Нельзя точно подогнать нелинейную модель (например, квадратичную) с помощью планов 2 (kp), однако, это можно сделать с помощью центральных композиционных планов.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Недостатки. Другим недостатком дробных планов является предположение о том, что взаимодействия высоких порядков отсутствуют, но иногда они действительно присутствуют. Например, если некоторые другие факторы установлены так, что оказывают отрицательное влияние на зависимый параметр. Однако в дробных факторных планах взаимодействия высоких порядков (выше двух), как правило, не будут обнаружены.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Максимально несмешанные 2(k-p) планы Дробные(k-p)факторные планы 2 часто используются в промышленных экспериментах, так как позволяют сокращать количество используемых данных. Предположим в качестве примера, что нужно изучить эффект воздействия на производственный процесс 11 переменных факторов, каждый из которых может быть установлен на 2 уровнях. Обозначим число факторов через k, в нашем примере это 11.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Эксперимент с полным факторным планом, когда изучаются эффекты каждой комбинации уровней каждого фактора, будет требовать проведения 2 k опытов, или 2048 в нашем случае.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Для уменьшения объема работ с данными инженер может решить отказаться от рассмотрения эффектов взаимодействий высоких порядков 11 факторов, и вместо этого сосредоточиться только на выявлении главных эффектов 11 факторов и некоторых эффектов взаимодействий низкого порядка, которые могут быть оценены с помощью эксперимента с меньшим, более разумным числом опытов. Существует другая, более теоретическая причина отказа от больших полных факторных 2 х уровневых экспериментов.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Обычно нелогично заниматься идентификацией эффектов взаимодействий факторов эксперимента высоких порядков, игнорируя нелинейные эффекты низкого порядка, такие как квадратичные и кубические эффекты, которые не могут быть оценены, если используются только 2 -х уровневые факторы. Таким образом, несмотря на то, что практические соображения часто приводят к необходимости экспериментов с малым числом опытов, это логически оправданно для таких экспериментов.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Альтернативой полного 2 k факторного плана является 2(k-p) дробный факторный план, который требует только "часть" данных, необходимых для полного факторного плана. В нашем примере с k=11 факторами, если могут быть проведены только 64 опыта, может быть построен 2(11 -5) дробный факторный план для эксперимента с 26 = 64 опытами. В сущности, построен полный k - p = 6 факторный план эксперимента с уровнями p факторов, "построенных" по уровням выбранных взаимодействий высокого порядка других 6 факторов.

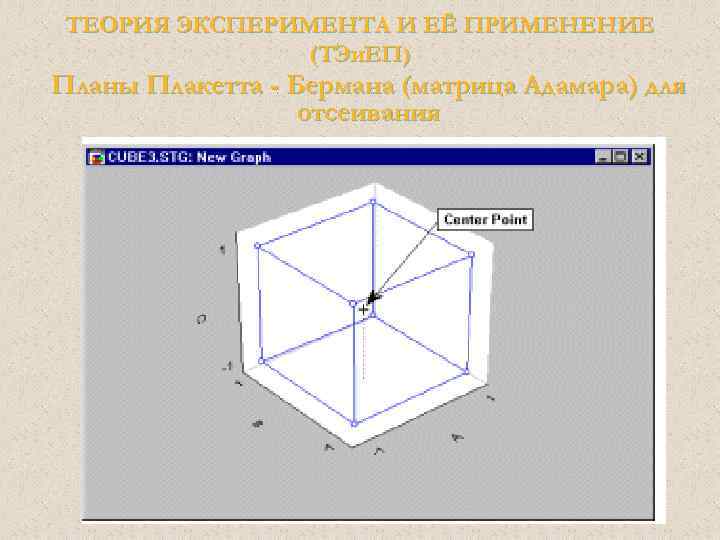
ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Дробные факторные "жертвуют" эффектами взаимодействий высокого порядка, но эффекты низкого порядка, могут еще быть вычислены корректно. Однако могут быть использованы различные критерии для выбора взаимодействий высокого порядка, используемых в качестве генераторов, среди которых некоторые критерии иногда приводят к различным "лучшим" планам.

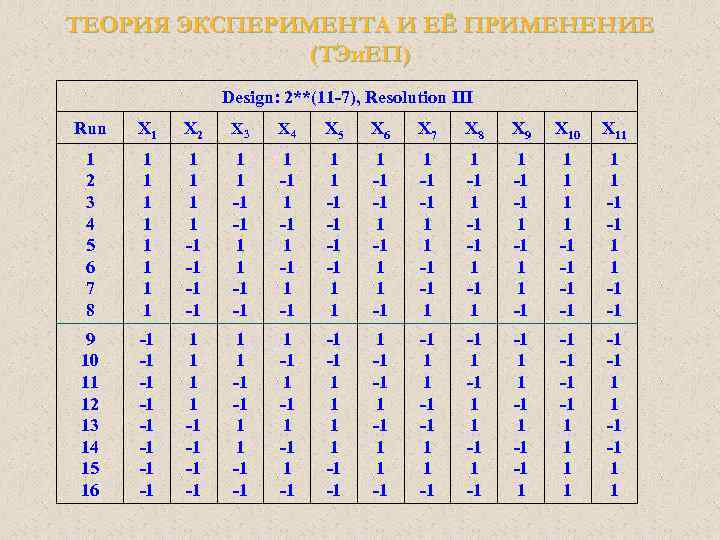ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Design: 2**(11 -7), Resolution III Run Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 Х 9 Х 10 Х 11 1 2 3 4 5 6 7 8 1 1 1 -1 -1 1 1 -1 -1 1 -1 -1 1 1 -1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 9 10 11 12 13 14 15 16 -1 -1 1 1 -1 -1 1 -1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 -1 1 1 -1 -1 1 1

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Критерий максимального разрешения плана. План, показанный в таблице результатов, характеризуется как 2**(11 -7) план разрешения III (три). Это означает, что вы исследуете всего k = 11 факторов, но p = 7 из них сгенерированы взаимодействиями полного 2**[(11 -7) = 4] факторного плана. В результате этот план не дает полного разрешения есть существуют некоторые , то эффекты взаимодействий, смешанные с другими эффектами.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания В общем случае план имеет разрешение R, когда в нем нет взаимодействий порядка l, смешанных с любыми другими взаимодействиями порядка, меньшего R - l. В нашем примере R равно 3. Здесь нет взаимодействий порядка l = 1 (т. е. главных эффектов), смешанных с любыми другими взаимодействиями порядка меньшего, чем R - l = 3 -1 = 2.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) Планы Плакетта - Бермана (матрица Адамара) для отсеивания Поэтому главные эффекты в этом плане не смешаны друг с другом, но смешаны с двухфакторными взаимодействиями, а следовательно, и с другими взаимодействиями более высокого порядка. Очевидным, но тем не менее очень важным общим критерием плана является то, что взаимодействия высшего порядка, используемые как генераторы, должны быть выбраны так, чтобы план имел максимально возможное разрешение.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Специальные вопросы возникают, когда анализируются смеси компонент, которые в сумме должны давать константу. Например, если вы хотите оптимизировать вкус фруктового пунша, состоящего из соков 5 фруктов, то сумма долей всех соков в каждой смеси должна быть равна 100%. Такая задача оптимизации смесей часто встречается в производстве пищи, очистке или производстве химикатов или лекарств.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Треугольные координаты Общим способом, с помощью которого могут быть представлены пропорции в смеси, являются треугольные диаграммы (диаграммы на треугольнике). Например, предположим, что у вас есть смесь, которая состоит из 3 компонент A , B, C. Любая смесь трех компонент может быть представлена точкой в системе координат на треугольнике, определяемой тремя переменными.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Треугольные координаты Например, возьмем следующие 6 смесей из 3 -х компонент. Х 1(А) Х 2(B) Х 3(C) 1 0 0 0. 5 0 0 1 0 0. 5

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Треугольные координаты Сумма для каждой смеси равна 1. 0, так что значения компонент в каждой смеси могут нтерпретироваться как пропорции. Если вы нанесете эти данные на график в виде обычной 3 -х мерной диаграммы рассеяния, станет очевидно, что точки образуют треугольник в 3 -х мерном пространстве. Только точки внутри треугольника, где сумма значений компонент равна 1, представляют настоящие смеси.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Треугольные координаты Следовательно, можно просто наносить данные только в треугольник (в данном случае двумерный), чтобы изображать значения компонент (пропорции) для каждой смеси.

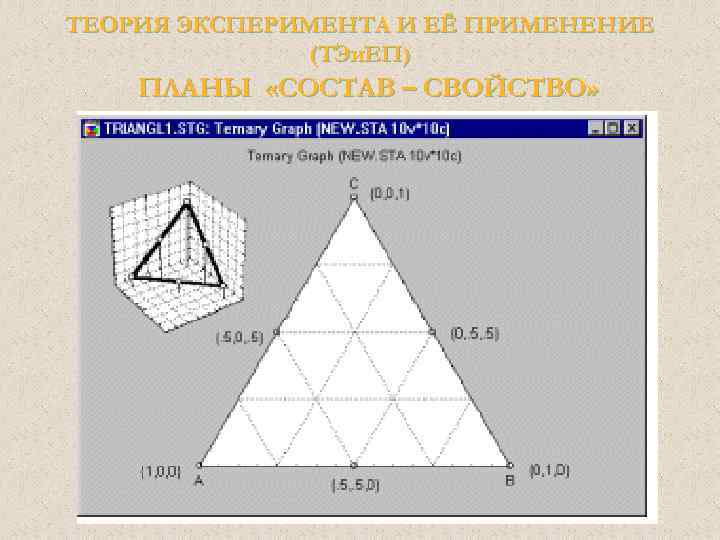ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО»

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Чтобы определить координаты точки в треугольном графике, вы соединяете прямой линией точку с вершинами треугольника.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Треугольные координаты Вершина, соответствующая конкретному фактору представляет собой чистую смесь, то есть состоящую только из данной компоненты. Так что координата соответствующей вершине компоненты равна 1 (или 100% или любой другой величине в зависимости от шкалирования) и равна 0 (нулю) для всех других компонент. На стороне, противоположной соответствующей вершине, значение данной компоненты равно 0 (нулю), а для других компонент. 5 (или 50% и так далее).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Тернарные поверхности и контуры Можно теперь добавить четвертое измерение и нанести на график значения зависимой переменной или функцию (поверхность) для каждой точки внутри треугольника. Заметим, что поверхность отклика может быть представлена либо в 3 -х мерном пространстве, где предсказываемый отклик (оценка Taste -Вкуса ) наносится, как расстояние поверхности от плоскости треугольника, либо представлена в виде контурной диаграммы, где контуры равной высоты наносятся в 2 -х мерном треугольнике.

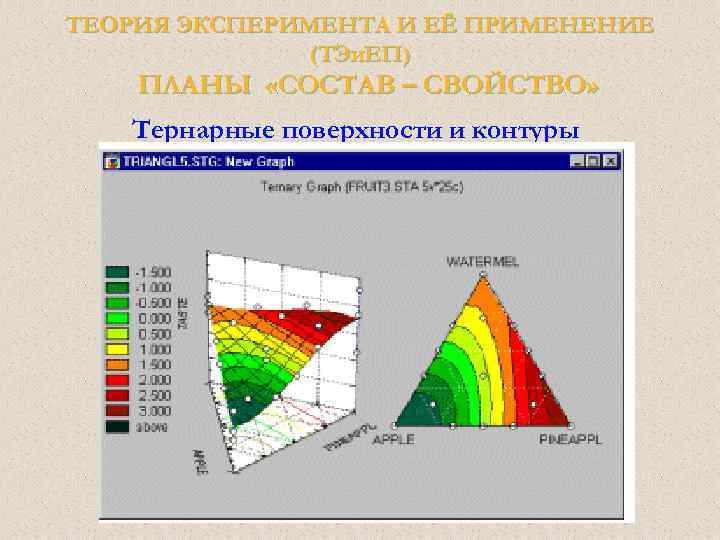ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Тернарные поверхности и контуры

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Тернарные поверхности и контуры Здесь следует упомянуть о том, что категоризованные графики позволяют построить категоризованные диаграммы, заданные на треугольнике. Они полезны, поскольку позволяют вам подгонять зависимую переменную (например, Taste -Вкус ) поверхностью отклика для различных уровней четвертой компоненты.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Канонический вид полиномов для смесей Подгонка поверхности отклика к данным по смесям, в принципе, осуществляется таким же образом, как и подгонка поверхности для данных, полученных, например, с помощью центральных компо зиционных планов. Однако имеется проблема, состоящая в том, что в данных о смесях накладывается ограничение, состоящее в том, что сумма значений компонент должна быть постоянной.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Канонический вид полиномов для смесей Рассмотрим простой пример с двумя факторами Х 1 (A) и Х 2 (B). Желательно подогнать простую линейную модель: Y = b 0 + b 1 Х 1 + b 2 Х 2 Здесь Y обозначает зависимую переменную, b 1 и b 2 обозначают коэффициенты регрессии, Х 1 и Х 2 значения факторов. Предпол ожим, что Х 1 и Х 2 должны в сумме давать 1; тогда вы можете умножить b 0 на 1 = (Х 1 + Х 2): Y = (b 0 Х 1 + b 0 Х 2) + b 1 Х 1 + b 2 Х 2

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Канонический вид полиномов для смесей или: y = b‘ 1 Х 1 + b‘ 2 Х 2 где b‘ 1 = b 0 + b 1 и b‘ 2 = b 0 + b 2. Таким образом, оценивание в этой модели сводится к подгонке модели множественной регрессии без свободного члена.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Общие модели для смесей Квадратичную и кубическую модели также можно упростить (как показано выше на примере простой линейной модели), что приводит к четырем стандартным моделям, обычно применяемым для подгонки смесей. Здесь приведены формулы для 3 -х переменных для таких моделей

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Общие модели для смесей Линейная модель : y = b 1 Х 1 + b 2 Х 2 + b 3 Х 3 Квадратичная модель : y = b 1 Х 1 + b 2 Х 2 + b 3 Х 3 + b 12 Х 1 Х 2 + b 13 Х 1 Х 3 + b 23 Х 2 Х 3 Специальная кубическая модель : y = b 1 Х 1 + b 2 Х 2 + b 3 Х 3 + b 12 Х 1 Х 2 + b 13 Х 1 Х 3 + b 23 Х 2 Х 3 + b 123 Х 1 Х 2 Х 3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Общие модели для смесей Полная кубическая модель : Y = b 1 Х 1 + b 2 Х 2 + b 3 Х 3 + b 12 Х 1 Х 2 + b 13 Х 1 Х 3 + b 23 Х 2 Х 3 + d 12 Х 1 Х 2(Х 1 - Х 2) + d 13 Х 1 Х 3(Х 1 - Х 3) + d 23 Х 2 Х 3(Х 2 - Х 3) + d 123 Х 1 Х 2 Х 3 (Заметим, что коэффициенты dij также являются параметрами модели).

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Стандартные планы экспериментов для смесей Обычно используются два типа стандартных планов экспериментов для смесей. Оба они оценивают поверхности отклика в вершинах треугольника и в центрах сторон. Иногда в эти планы добавляют дополнительные внутренние точки.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Стандартные планы экспериментов для смесей Симплекс-вершинные планы. При этом размещении точек плана m+1 для каждого фактора или компоненты в модели тестируются равноразмещенные точки: Xi = 0, 1/m, 2/m, . . . , 1 i = 1, 2, . . . , q а также все их комбинации. Получающийся план называется simplex-lattice – симплекс-вершинным планом. Например, симплекс-вершинный план с {q=3, m=2} включает следующие смеси:

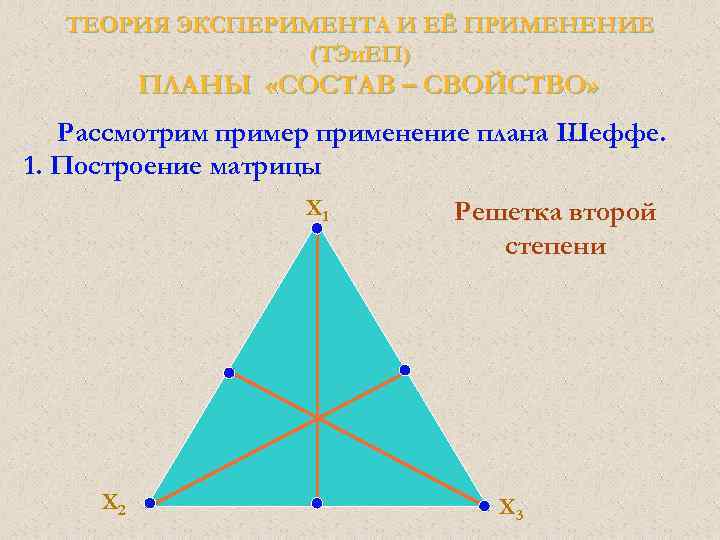ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Рассмотрим пример применение плана Шеффе. 1. Построение матрицы Х 1 Х 2 Решетка второй степени Х 3

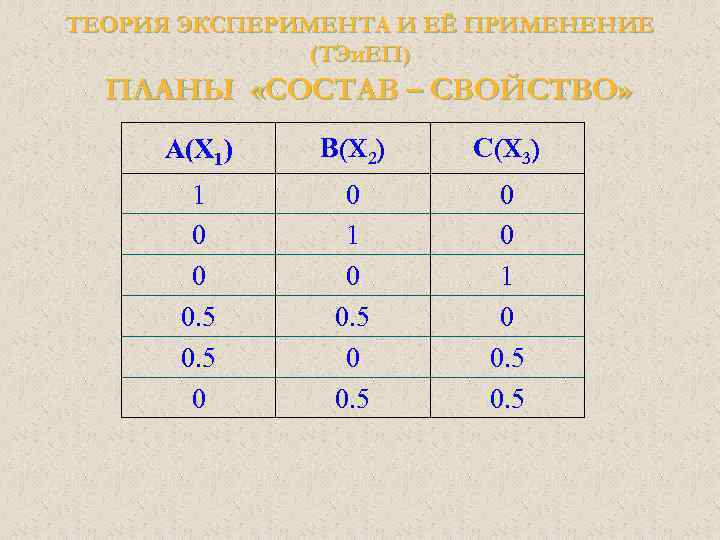ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» A(X 1) B(X 2) C(X 3) 1 0 0 0. 5 0 0 1 0 0. 5

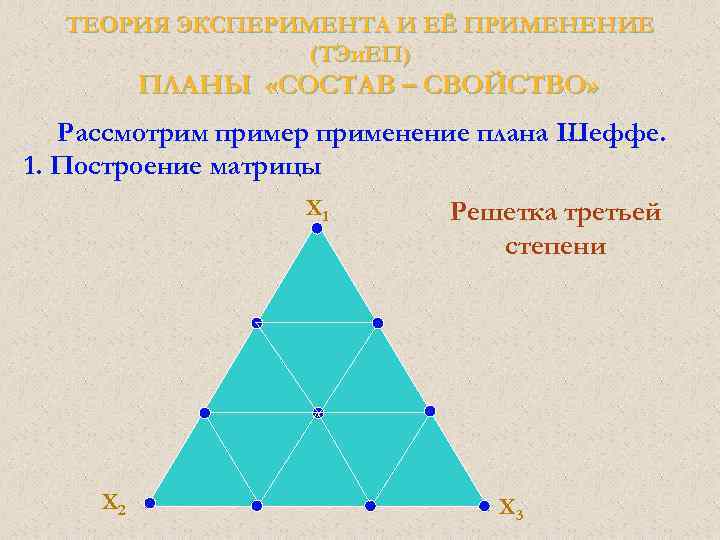ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Рассмотрим пример применение плана Шеффе. 1. Построение матрицы Х 1 Х 2 Решетка третьей степени Х 3

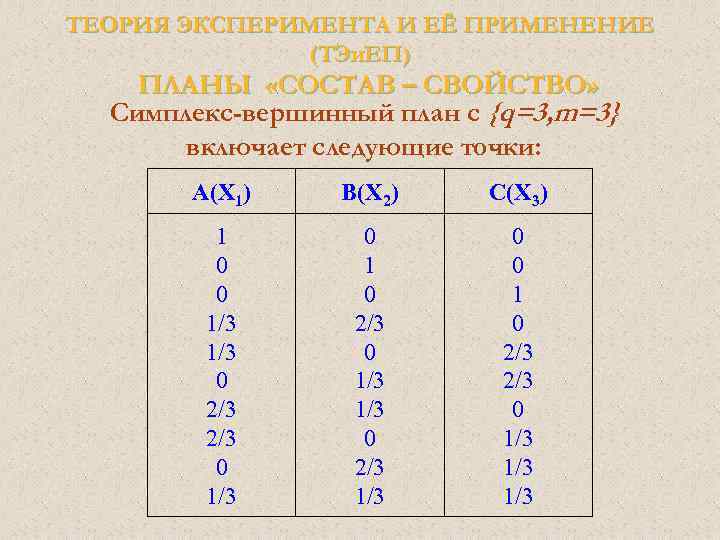ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Симплекс-вершинный план с {q=3, m=3} включает следующие точки: A(X 1) B(X 2) C(X 3) 1 0 0 1/3 0 2/3 0 1/3 0 1 0 2/3 0 1/3 0 2/3 1/3 0 0 1 0 2/3 0 1/3 1/3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ ШЕФФЕ «СОСТАВ – СВОЙСТВО» Стандартные планы экспериментов для смесей Симплекс-центроидные планы. Альтернативное размещение факторов, введенное Шеффе (Scheffe, 1963), является так называемым симплекс-центроидным планом. При его применении точки плана соответствуют всем перестановкам чистых смесей (например, 1 0 0 ; 0 1 0 ; 0 0 1 ), перестановкам бинарных смесей (Ѕ Ѕ 0 ; Ѕ 0 Ѕ ; 0 Ѕ Ѕ), перестановкам с тремя одинаковыми по пропорции компонентами и так далее. Например, для 3 -х факторов симплекс-центроидный план состоит из точек (вершины, центры сторон, центр треугольника):

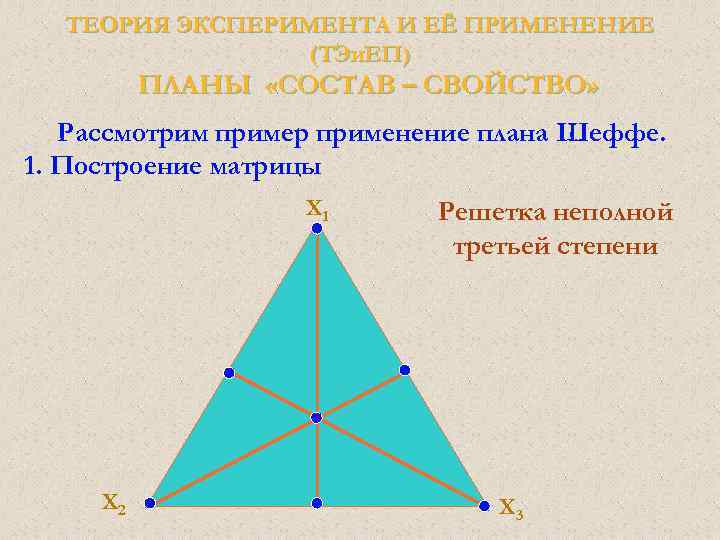ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Рассмотрим пример применение плана Шеффе. 1. Построение матрицы Х 1 Х 2 Решетка неполной третьей степени Х 3

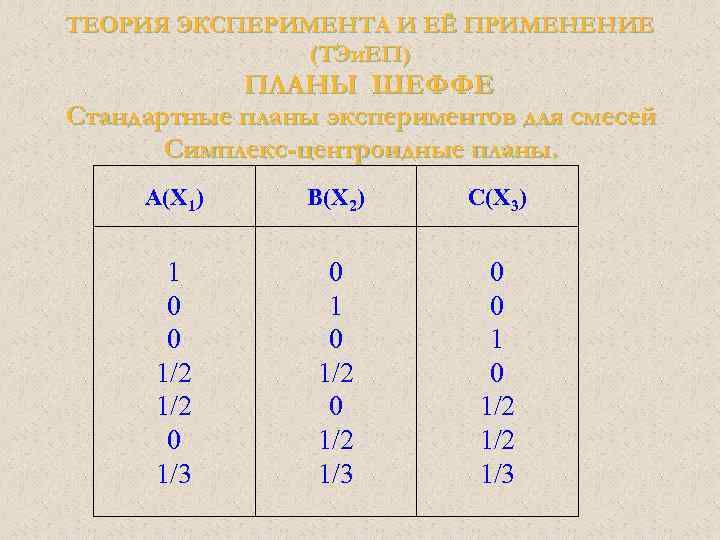ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ ШЕФФЕ Стандартные планы экспериментов для смесей Симплекс-центроидные планы. A(X 1) B(X 2) C(X 3) 1 0 0 1/2 0 1/3 0 1/2 1/3 0 0 1/2 1/3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ ШЕФФЕ «СОСТАВ – СВОЙСТВО» Стандартные планы экспериментов для смесей Симплекс-центроидные планы. Добавление внутренних точек. Подобные планы иногда дополняются внутренними точками Например, для 3 -х факторов можно добавить следующие внутренние точки:

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ ШЕФФЕ «СОСТАВ – СВОЙСТВО» Стандартные планы экспериментов для смесей Симплекс-центроидные планы. A(X 1) B(X 2) C(X 3) 2/3 1/6 1/6 1/6 2/3 Если нанести их на диаграмму рассеяния в треугольных координатах, можно увидеть, как ровно эти планы заполняют экспериментальную область, определенную на треугольнике.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ ШЕФФЕ «СОСТАВ – СВОЙСТВО» Стандартные планы экспериментов для смесей Симплекс-центроидные планы. Ограничения снизу Для всех планов, описанных выше, требуются точки -вершины, то есть чистые смеси, состоящие из одной компоненты. На практике такие точки обычно неприемлемы, т. к. не могут производиться из-за соображений стоимости или других ограничений. Такого рода ограничения весьма типичны.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ ШЕФФЕ «СОСТАВ – СВОЙСТВО» Стандартные планы экспериментов для смесей Симплекс-центроидные планы. Ограничения снизу Рассмотрим пример с тремя компонентами, где на компоненту Х 1(A) наложено ограничение Х 1 ≥ 3 Общая сумма для 3 -х компонентной смеси должна быть равной 1. Это ограничение может быть показано на треугольной диаграмме в виде прямой с треугольными координатами для x. A=. 3 , то есть прямой, параллельной стороне треугольника, противоположной вершине A.

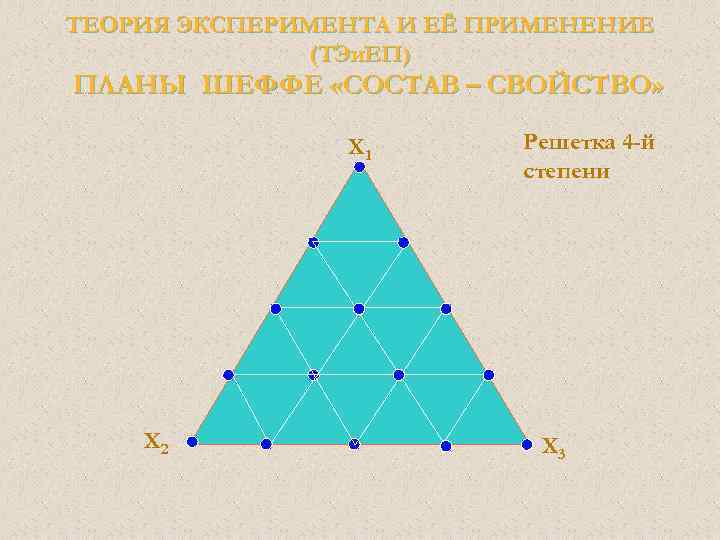ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ ШЕФФЕ «СОСТАВ – СВОЙСТВО» Х 1 Х 2 Решетка 4 -й степени Х 3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ ШЕФФЕ «СОСТАВ – СВОЙСТВО» Стандартные планы экспериментов для смесей Симплекс-центроидные планы. Ограничения сверху и снизу Если имеются ограничения снизу и сверху (что часто бывает в экспериментах на смесях), то стандартные симплекс-вершинные и симплексцентроидные планы не могут быть построены, поскольку область, определяемая ограничениями, не является больше треугольником и центры (например, вершины) могут не принадлежать области определения.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Выводы. Когда исследователь разрабатывает продукт, для которого известно, что его свойства зависят от его "ингредиентов", создание лучшего продукта, возможно, требует определения эффектов его ингредиентов на каждое свойство продукта в отдельности и последующее нахождение гармонического сочетания ингредиентов, оптимизирующего общую желательность продукта.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» В терминах анализа данных, процедура, которая производит максимизацию желательности продукта, делает следующее: (1) находит адекватные модели (т. е. уравнения предсказания) для предсказания свойств продукта как функцию уровней независимых переменных, и (2) определяет оптимальные уровни независимых переменных для получения высокого общего качества продукта.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Эти два шага, если им точно следовать, с большой вероятностью приводят к большему успеху в усовершенствовании продукта, чем придуманная, но статистически сомнительная методика надежды на случайные достижения и открытия, которые радикально улучшили бы качество продукта.

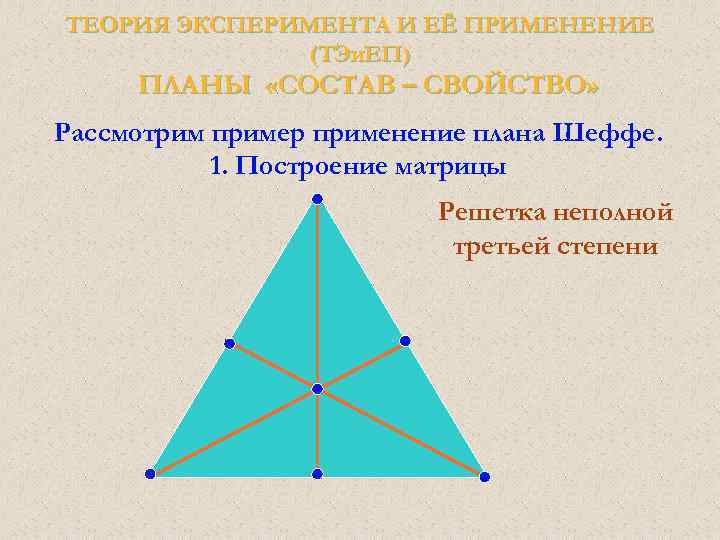ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» Рассмотрим пример применение плана Шеффе. 1. Построение матрицы Решетка неполной третьей степени

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» 1. Построение матрицы U 1 2 3 4 5 6 7 X 1 1 0 0 1/2 0 1/3 X 2 0 1/2 1/3 X 3 0 0 1/2 1/3 Y 1 (доход) Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7

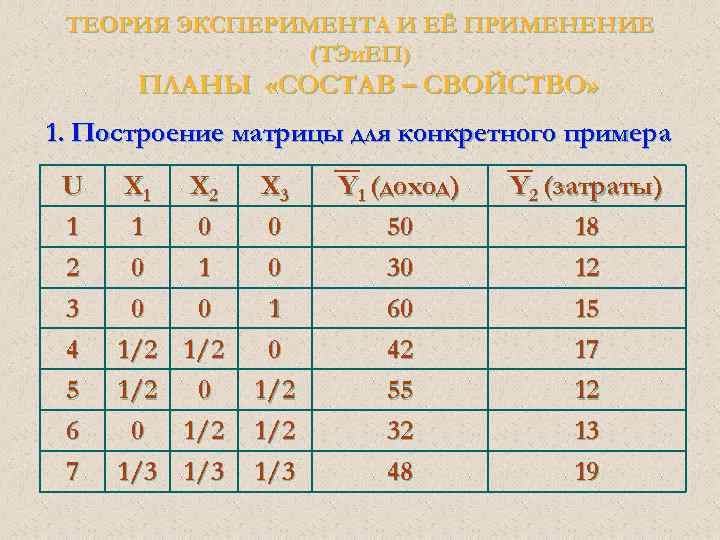ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» 1. Построение матрицы для конкретного примера U 1 2 3 4 5 6 7 X 1 1 0 0 1/2 0 1/3 X 2 0 1/2 1/3 X 3 0 0 1/2 1/3 Y 1 (доход) 50 30 60 42 55 32 48 Y 2 (затраты) 18 12 15 17 12 13 19

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» 1. Построение матрицы Общий вид уравнения Шеффе при к = 3 Y=b 1 X 1+b 2 X 2+b 3 X 3+b 12 X 1 X 2+b 13 X 1 X 3+ +b 23 X 2 X 3+b 123 X 1 X 2 X 3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» 2. Составим уравнение для Y 1 – доход и Y 2 – затраты А) Для Y 1: вычисляем коэффициенты для уравнения дохода b 1 = Y 1 = 50; b 2 = Y 2 = 30; b 3 = Y 3 = 60; b 12 = 4 Y 12 – 2 Y 1 – 2 Y 2 = 4*42 – 2*50 – 2*30 = 8 b 13 = 4 Y 13 – 2 Y 1 – 2 Y 3 = 4*55 – 2*50 – 2*60 = 0 b 23 = 4 Y 23 – 2 Y 2– 2 Y 3 = 4*32 – 2*30 – 2*60 = - 52 b 123 = 4 Y 123 – 12(Y 12+ Y 13+Y 23) +3(Y 1+Y 2+Y 3)= 27*48 – 12(42+55+32) + 3(50+30+60)= 168

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» 2. Составим уравнение для Y 1 – доход и Y 2 – затраты А) Для Y 1: получили уравнение: Y 1 = 50 X 1+30 X 2+60 X 3+8 X 1 X 2 -52 X 2 X 3+168 X 1 X 2 X 3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» 2. Составим уравнение для Y 1 – доход и Y 2 – затраты А) Для Y 2 вычисляем коэффициенты для уравнения затрат: b 1 = Y 1 = 18; b 2 = Y 2 = 12; b 3 = Y 3 = 15; b 12 = 4 Y 12 – 2 Y 1 – 2 Y 2 = 4*17 – 2*18 – 2*12 = 8 b 13 = 4 Y 13 – 2 Y 1 – 2 Y 3 = 4*12 – 2*18 – 2*15 = -18 b 23 = 4 Y 23 – 2 Y 2– 2 Y 3 = 4*14 – 2*15 – 2*17 = -8 b 123 = 4 Y 123 – 12(Y 12+ Y 13+Y 23) +3(Y 1+Y 2+Y 3)= 27*19 – 12(17+12+13) + 3(18+12+15)= 144

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» 2. Составим уравнение для Y 1 – доход и Y 2 – затраты А) Для Y 1: получили уравнение: Y 1 = 18 X 1+12 X 2+15 X 3+8 X 1 X 2 -18 X 1 X 3 -8 X 2 X 3+144 X 1 X 2 X 3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ (ТЭи. ЕП) ПЛАНЫ «СОСТАВ – СВОЙСТВО» 3. Построение XI X 1 66 Результаты симплекса: X 64 65 вычислений по IX 61 63 параметру доход VIII 57 60 сведем в таблицу 52 VII VI V IV III II I X 2 56 46 39 31 51 45 38 30 22 12 1 21 2 3 4 5 6 7 8 9 10 11 X 3

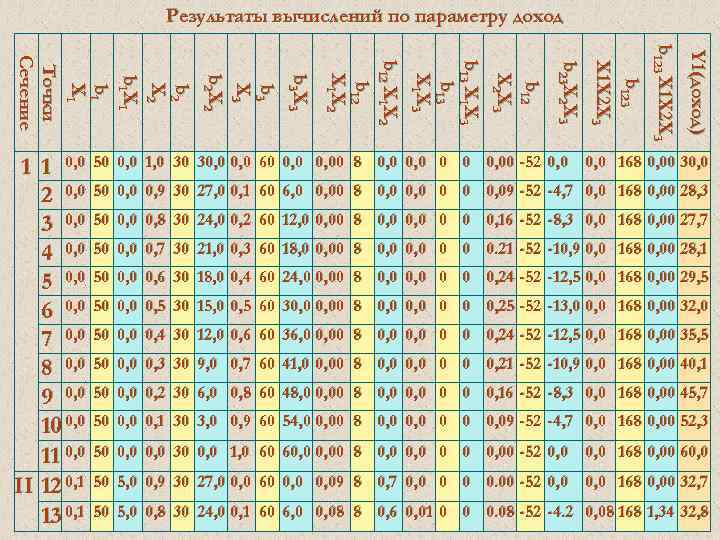Результаты вычислений по параметру доход Y 1(доход) b 123 X 1 X 2 X 3 X 1 X 2 X 3 b XX b 23 X 2 X 3 b 12 b 1 2 X 2 X 3 b 13 X 1 X 3 b 1 3 X 1 X 3 X 1 X 3 b XX b 1 2 X 1 X 2 b b 1 2 XX X 1 X 2 b 3 X 3 b 3 X 3 b 2 X 2 b b 2 X X 2 b. X b 1 X 1 b 1 X X 1 Т о чки С е ч е ние 1 1 0, 0 2 0, 0 3 0, 0 4 0, 0 5 0, 0 6 0, 0 7 0, 0 8 0, 0 9 0, 0 10 0, 0 11 0, 0 II 12 0, 1 13 0, 1 50 0, 0 1, 0 30 30, 0 60 0, 00 8 0, 0 0 0 0, 00 -52 0, 0 168 0, 00 30, 0 50 0, 9 30 27, 0 0, 1 60 6, 0 0, 00 8 0, 0 0 0 0, 09 -52 -4, 7 0, 0 168 0, 00 28, 3 50 0, 8 30 24, 0 0, 2 60 12, 0 0, 00 8 0, 0 0 0 0, 16 -52 -8, 3 0, 0 168 0, 00 27, 7 50 0, 7 30 21, 0 0, 3 60 18, 0 0, 00 8 0, 0 0 0 0. 21 -52 -10, 9 0, 0 168 0, 00 28, 1 50 0, 6 30 18, 0 0, 4 60 24, 0 0, 00 8 0, 0 0 0 0, 24 -52 -12, 5 0, 0 168 0, 00 29, 5 50 0, 5 30 15, 0 0, 5 60 30, 00 8 0, 0 0 0 0, 25 -52 -13, 0 0, 0 168 0, 00 32, 0 50 0, 4 30 12, 0 0, 6 60 36, 0 0, 00 8 0, 0 0 0 0, 24 -52 -12, 5 0, 0 168 0, 00 35, 5 50 0, 3 30 9, 0 0, 7 60 41, 0 0, 00 8 0, 0 0 0 0, 21 -52 -10, 9 0, 0 168 0, 00 40, 1 50 0, 2 30 6, 0 0, 8 60 48, 0 0, 00 8 0, 0 0 0 0, 16 -52 -8, 3 0, 0 168 0, 00 45, 7 50 0, 1 30 3, 0 0, 9 60 54, 0 0, 00 8 0, 0 0 0 0, 09 -52 -4, 7 0, 0 168 0, 00 52, 3 50 0, 0 30 0, 0 1, 0 60 60, 00 8 0, 0 0 0 0, 00 -52 0, 0 168 0, 00 60, 0 50 5, 0 0, 9 30 27, 0 0, 0 60 0, 09 8 0, 7 0, 0 0. 00 -52 0, 0 168 0, 00 32, 7 50 5, 0 0, 8 30 24, 0 0, 1 60 6, 0 0, 08 8 0, 6 0, 01 0 0 0. 08 -52 -4. 2 0, 08 168 1, 34 32, 8

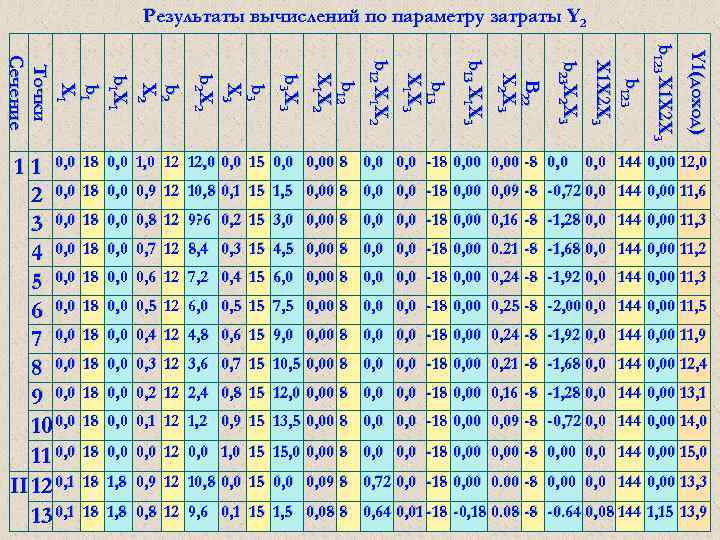Результаты вычислений по параметру затраты Y 2 Y 1(доход) b 123 X 1 X 2 X 3 X 1 X 2 X 3 b XX b 23 X 2 X 3 B 22 X 2 X 3 b 13 X 1 X 3 b 1 3 X 1 X 3 b 1 3 XX X 1 X 3 b 12 X 1 X 2 b 1 2 X 1 X 2 X 1 X 2 b 3 X 3 b 3 X X 3 b 2 X 2 b 2 X 2 b 1 X 1 b 1 b 1 X 1 Т о чки С е ч е ние 1 1 0, 0 2 0, 0 3 0, 0 4 0, 0 5 0, 0 6 0, 0 7 0, 0 8 0, 0 9 0, 0 10 0, 0 11 0, 0 II 12 0, 1 13 0, 1 18 0, 0 12 12, 0 0, 0 15 0, 00 8 0, 0 -18 0, 00 -8 0, 0 144 0, 00 12, 0 18 0, 0 0, 9 12 10, 8 0, 1 15 1, 5 0, 00 8 0, 0 -18 0, 00 0, 09 -8 -0, 72 0, 0 144 0, 00 11, 6 18 0, 0 0, 8 12 9? 6 0, 2 15 3, 0 0, 00 8 0, 0 -18 0, 00 0, 16 -8 -1, 28 0, 0 144 0, 00 11, 3 18 0, 0 0, 7 12 8, 4 0, 3 15 4, 5 0, 00 8 0, 0 -18 0, 00 0. 21 -8 -1, 68 0, 0 144 0, 00 11, 2 18 0, 0 0, 6 12 7, 2 0, 4 15 6, 0 0, 00 8 0, 0 -18 0, 00 0, 24 -8 -1, 92 0, 0 144 0, 00 11, 3 18 0, 0 0, 5 12 6, 0 0, 5 15 7, 5 0, 00 8 0, 0 -18 0, 00 0, 25 -8 -2, 00 0, 0 144 0, 00 11, 5 18 0, 0 0, 4 12 4, 8 0, 6 15 9, 0 0, 00 8 0, 0 -18 0, 00 0, 24 -8 -1, 92 0, 0 144 0, 00 11, 9 18 0, 0 0, 3 12 3, 6 0, 7 15 10, 5 0, 00 8 0, 0 -18 0, 00 0, 21 -8 -1, 68 0, 0 144 0, 00 12, 4 18 0, 0 0, 2 12 2, 4 0, 8 15 12, 0 0, 00 8 0, 0 -18 0, 00 0, 16 -8 -1, 28 0, 0 144 0, 00 13, 1 18 0, 0 0, 1 12 1, 2 0, 9 15 13, 5 0, 00 8 0, 0 -18 0, 00 0, 09 -8 -0, 72 0, 0 144 0, 00 14, 0 18 0, 0 12 0, 0 15 15, 0 0, 00 8 0, 0 -18 0, 00 -8 0, 00 0, 0 144 0, 00 15, 0 18 1, 8 0, 9 12 10, 8 0, 0 15 0, 09 8 0, 72 0, 0 -18 0, 00 0. 00 -8 0, 00 0, 0 144 0, 00 13, 3 18 1, 8 0, 8 12 9, 6 0, 1 15 1, 5 0, 08 8 0, 64 0, 01 -18 -0, 18 0. 08 -8 -0. 64 0, 08 144 1, 15 13, 9

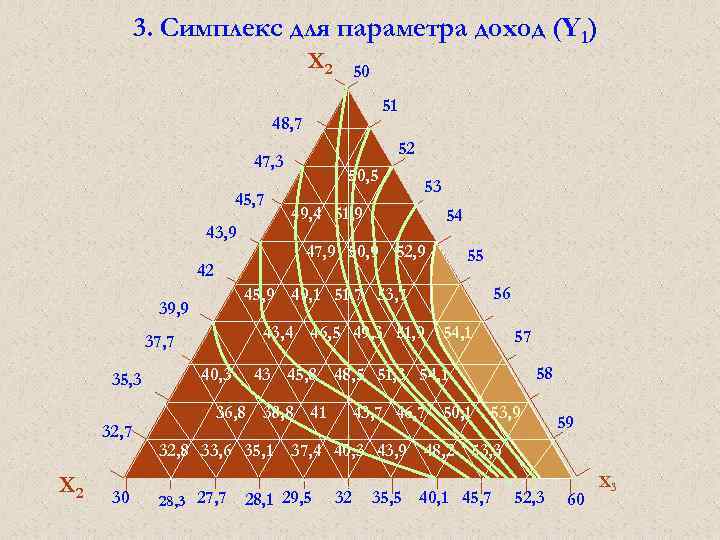3. Симплекс для параметра доход (Y 1) X 2 50 51 48, 7 52 47, 3 45, 7 43, 9 30 54 43, 4 46, 5 49, 3 51, 9 37, 7 X 2 49, 4 51, 9 55 56 45, 9 49, 1 51, 7 53, 7 39, 9 32, 7 53 47, 9 50, 9 52, 9 42 35, 3 50, 5 40, 3 57 58 43 45, 8 48, 5 51, 3 54, 1 43, 7 46, 7 50, 1 36, 8 38, 8 41 32, 8 33, 6 35, 1 28, 3 27, 7 54, 1 53, 9 59 37, 4 40, 3 43, 9 48, 2 53, 3 28, 1 29, 5 32 35, 5 40, 1 45, 7 52, 3 60 X 3

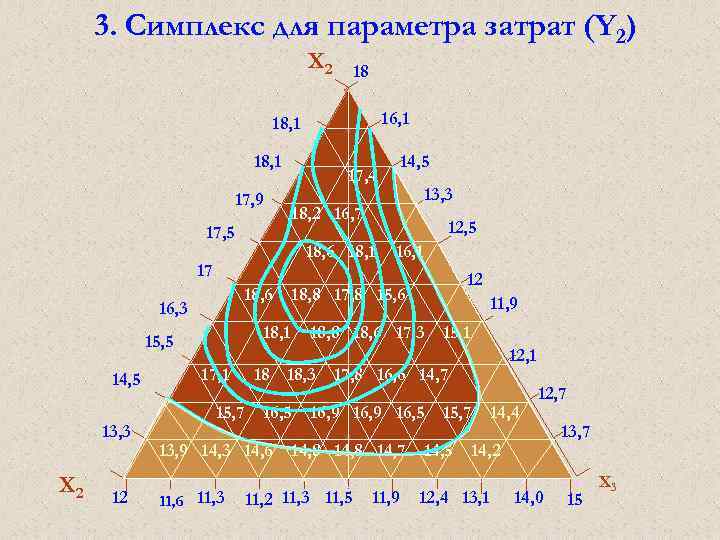3. Симплекс для параметра затрат (Y 2) X 2 18 16, 1 18, 1 17, 9 17, 5 17, 4 17 16, 3 14, 5 13, 3 X 2 12 17, 1 15, 7 16, 1 12 11, 9 18, 8 18, 6 17, 3 18 18, 3 16, 5 13, 9 14, 3 14, 6 11, 3 12, 5 18, 8 17, 8 15, 6 18, 1 15, 5 13, 3 18, 2 16, 7 18, 6 18, 1 18, 6 14, 5 15, 1 12, 1 17, 8 16, 6 14, 7 16, 9 16, 5 14, 8 14, 7 11, 2 11, 3 11, 5 11, 9 15, 7 14, 5 14, 4 12, 7 14, 2 12, 4 13, 1 14, 0 13, 7 15 X 3

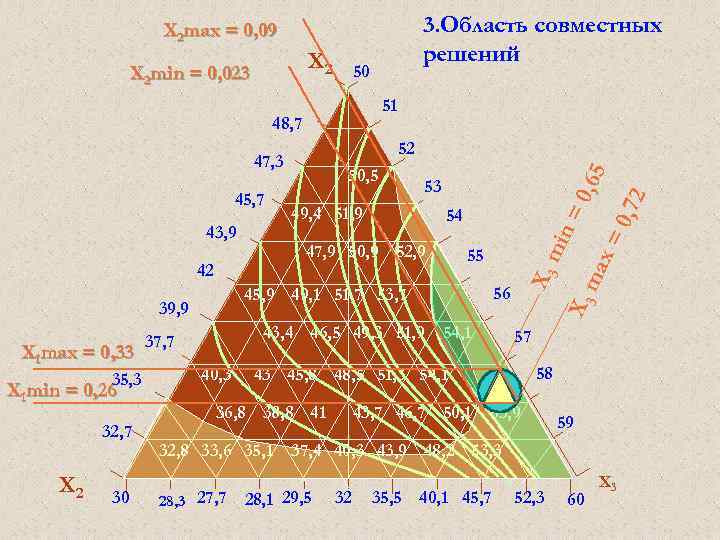3. Область совместных решений Х 2 max = 0, 09 X 2 Х 2 min = 0, 023 50 51 48, 7 Х 1 min = 0, 26 32, 7 X 2 30 Х 3 , 72 Х 3 56 =0 55 45, 9 49, 1 51, 7 53, 7 39, 9 35, 3 54 47, 9 50, 9 52, 9 42 Х 1 max = 0, 33 49, 4 51, 9 ma x 43, 9 53 mi n= 45, 7 50, 5 0, 6 5 52 47, 3 43, 4 46, 5 49, 3 51, 9 37, 7 40, 3 57 58 43 45, 8 48, 5 51, 3 54, 1 43, 7 46, 7 50, 1 36, 8 38, 8 41 32, 8 33, 6 35, 1 28, 3 27, 7 54, 1 53, 9 59 37, 4 40, 3 43, 9 48, 2 53, 3 28, 1 29, 5 32 35, 5 40, 1 45, 7 52, 3 60 X 3

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап I. Планирование эксперимента Шаг Наименование шага Примечание 1 2 Выбор процесса (установки) для проведения анализа Постановка Выбор зоны оптимальных задачи значений выхода (область эксперимента совместного решения) 3 Выбор критериев оптимизации Например, Y 1 (Т) – Технический (технологический) – производительность (доход) – Т max; Y 2 (Э) – экономический – затраты – Э min

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап I. Планирование эксперимента Шаг Наименование шага 4 Выбор факторов влияющих на критерии оптимизации 5 Выбор диапазона варьирования факторов Постановка отсеивающего эксперимента и окончательный выбор варьируемых факторов 6 Примечание X 1, Х 2, … Хn – регулируемые параметры от которых зависит выход (Y) При необходимости (при k > 7, желательно)

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап I. Планирование эксперимента Шаг Наименование шага Примечание 7 Выбор уровня стабилизации неварьируемых факторов Для малозначимых факторов выбирается некоторый оптимальный уровень известный по предварительным данным 8 Кодирование факторов Векторное изображение факторов и матричное представление уровней факторов

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап I. Планирование эксперимента Шаг Наименование шага Примечание 9 Выбор математической модели и вида поверхности отклика по основному (техническому) отклику Из предварительного опыта и литературных данных. При их отсутствии выбирается простейшая модель (линейная) и производится постепенное итерационное уточнений в дальнейшем 10 Выбор плана ПФЭ, или план «состав – свойства» , и т. д.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап I. Планирование эксперимента Шаг Наименование шага Примечание 11 Построение матрицы плана 12 Выбор числа повторностей опытов По таблице больших чисел (φ = 3, достаточно для большинства экспериментов) 13 Рандомизация опытов По таблице случайных чисел (случайный выбор проведение опытов и их повторностей)

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап II Проведение эксперимента Шаг Наименование шага 14 Устанавливаем значение факторов для случайно выбранного опыта (его повторности) согласно матрице плана (I – 7) и матричному представлению факторов (I – 6). Включаем установку или запускаем процесс. После получения выхода, замеряем значение технического параметра и экономического параметра и заносим их в матрицу эксперимента в соответствующую графу (№ варианта и № повторности). Повторяем действия для следующего опыта (повторности) и т. д. до полного перебора всех вариантов.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап III. Обработка экспериментальных данных и получение математической модели процесса (установки) Шаг Наименование шага 15 Дисперсионный анализ 1. Вычисление среднеарифметического значения критериев оптимизации (откликов) 2. Определение равноточности результатов эксперимента по критерию Кохрена для всех откликов Примечание Из полученных значений повторностей по опыту GЭ > GТ [α, f 1=(φ1), f 2=N]

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап III. Шаг Наименование шага 15 3. Определить среднеквадратическую ошибку для откликов 4. Вычислит значения коэффициентов регрессионных уравнений для откликов 5. Проверить правильность вычисления коэффициентов уравнений для откликов Примечание S = √S 2 Xijk. Yu) Сравнение опытных и расчетных данных и ошибки для одной из точек плана

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап III. Шаг Наименование шага Примечание 15 6. Оценить ошибку в S{bi}= Sy / √N; вычислении коэффициентов регрессионных уравнений bi = bi ± S{bi} 7. Проверить коэффициенты регрессии уравнений на значимость по критерии Стьюдента 8. Оценить адекватность уравнений регрессии по критерию Фишера t. Э ≤ t. Т[α, f 2=N(φ-1)], коэффициент незначим FЭ ≤ FТ[α, f 1= = N(φ-1), f 2=N-k при N≠k]

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап III. Шаг Наименование шага Примечание 16 Регрессионный анализ (Количественный и качественный анализы для математических моделей процесса (установки)) 1. Построить пространственную модель факторного пространства или его сечений 2. Выбрать грань при условии Т max; Э min Для 3 -х факторного пространства – куб. Качественный анализ моделей. Выбирается грань (предельное значение для одного из Х) при котором Y = maх)

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап III. Шаг 16 Наименование шага 3. Построить поверхности отклика на выбранной грани (для технического и экономического откликов) 4. Построить семейства изолиний и градиенты на выбранной грани Примечание Трехмерное изображение поверхности отклика на этой грани (когда ось стабилизированного фактора заменена откликом) для технического и экономического откликов

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Этап III. Шаг 16 Наименование шага 5. Методом итераций найти область совместных решений 6. Описать область совместных решений Примечание в кодах и натуральных значениях факторов

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Алгоритм использования ТЭ Дальнейшие этапы. Этап Наименование этапа IV Экспериментальная проверка полученных значений оптимальной области совместных решений. V Интерполяция полученной модели в направлении градиента VI Построение новой математической модели процесса (установки) в уточненном факторном пространстве (переход к шагу 5 первого этапа)

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Симплексный метод оптимизации. Симплексом называется правильный многогранник, имею щийп+1 вершину, где п—число факторов, влияющих на процесс. Так, например, если факторов два, то симплексом является правильный треугольник.

ТЕОРИЯ ЭКСПЕРИМЕНТА И ЕЁ ПРИМЕНЕНИЕ Симплексный метод оптимизации.