Теория автоматического управления электромеханическими системами ТАУ ЭМС

Теория автоматического управления электромеханическими системами (ТАУ ЭМС)

1. Классификация САУ ЭМС • 1. По наличию обратной связи : • • • 1. 1. Разомкнутые. Как правило, отсутствует система контроля состояния, либо результаты контроля только регистрируются, но не используются для коррекции состояния. Системы без обратной связи (без ОС) применяются для простейших механизмов, где не требуется точного поддержания состояния, либо априорно известно, совокупность возмущений не приводит к недопустимым отклонениям состояния от требуемого.

• 1. 2. В замкнутых системах (в системах с ОС ) состояние элементов системы контролируется при помощи датчиков – устройств, предназначенных для измерения контролируемой переменной и преобразования в форму, удобную для дальнейшей обработки. Например, скорость вращения вала двигателя можно измерить тахогенератором, ток якоря двигателя пропорционален падению напряжения на небольшом сопротивлении (шунте), включенном последовательно с обмоткой якоря. Результаты измерения в дальнейшем используются для формирования управляющего воздействия, которое предназначено для коррекции состояния объекта с целью приведения его к заданному.

• 2. По функциональному назначению: • 2. 1. Системы стабилизации • Предназначены для поддержания требуемого состояния системы. Например, система стабилизации скорости, система стабилизации положения механизма. В таких системах основ ными режимами работы являются режимы поддержания заданного состояния, а режим пере хода из одного состояния в другое является вспомогательным. При проектировании и на стройке таких систем параметры регулятора выбираются исходя из требований реакции сис темы на возмущающее воздействие.

• • 2. 2. Когда система работает в режиме частого либо постоянного изменения состояния, регулятор синтезируется исходя из требований, предъявляемых к динамике системы при управляющих воздействиях. 3. Системы управления положением механизма. 3. 1. Система стабилизации положения. 3. 2. Позиционные системы или системы управления конечным состоянием. 3. 2. 1. Терминальные системы, в которых важно положение системы в конечной точке траектории, сама траектория движения к конечной точке может быть произвольной. 3. 2. 2. В квазитерминальных системах важна не только точность положения механизма в конеч ной точке траектории но и точность перемещения по заданной траектории. .

• 3. 4. Следящие системы. Такие системы предназначены для воспроизведения входных воздействий произвольной формы. • Регулятор строится таким образом , чтобы система обеспечивала заданную точность воспроизведения входного воздействия при известных предельных параметрах входного воздействия; максимальной амплитуде; макси мальной скорости; максимальном ускорении. То есть критерием качества следящей системы является min Q, либо Q ≤ Qзад. Параметры переходного процесса, как правило используются в качестве ограничений.

• 4. По принципу построения. • 4. 1. По отклонению. • Система реагирует на отклонение от требуемого состояния, возникающего в результате действия возмущений. Естественно система реагирует на возмущение с запаздыванием в силу инерционности ее элементов. • 4. 2. По возмущению. • В системах управления по возмущению искусственно создают второй канал распространения возмущения ( первый естественный). Функциональная схема такой системы представлена на рис. 1.

• Основной контур системы включает в себя объект управления (ОУ), регулятор (РЕГ) и сис тему контроля состояния системы (СК). На объект действует возмущение, основным каналом рас пространения которого является естественный. Во второй канал входят блоки: СКВ система контроля возмущения; ИК устройство преобразу ющее информацию о возмущении таким образом, чтобы реакция системы на возмущающее воздействие была минимальной. Рис. 1 Функциональна инвариантной системы схема

• Техническая реализация ИК, позволяющего полностью скомпенсировать действие возмущения, как правило, невозможна, то есть невозможна техническая реализация инва риантной системы. На практике применяют так называемую квазиинвариантную систему или инвариант ную до ‘ε’, которая уже технически реализуема, однако не позволяет скомпенсиро вать полностью действие возму щения. Можно утверждать, что • где отклонение состояния системы от заданного при отсутствии второго канала, • отклонение состояния системы от заданного в квазиинвариантной системе, • отклонение состояния системы от заданного в инвариантной системе • Еще одна проблема возникает при технической реализации таких систем это, как правило, сложность контроля возмущающего воздействия

• • 5. Оптимальные. Этот класс систем обеспечивает экстремаль ное значение какого либо наперед заданного кри терия качества системы, например, минимум зат рат энергии, максимум производительности, максимальное быстродействие (минимум времени переходного процесса, максимум производительности ), и т. д. . • 6. Адаптивные • Адаптивные системы применяются в условиях изменяющихся параметров самой системы, либо внешней среды. Такая система приспосабливается к изменяющимся условиям работы ( настраивает ся на текущие условия работы).

• 6. 1. Системы с сигнальной настройкой. • 6. 1. 1. Системы с эталонной модель. • Систему строят таким образом, чтобы она имела динамические свойства системы имеющей передаточную функцию (эталонной модели), то есть эталонная модель должна быть включена в систему таким образом, чтобы сообщить системе в целом свои свойства. На рис. 2 приведен показан один из возможных способов реализации адаптивной системы с эталонной моделью. Рис. 2 Система с эталонной моделью

• На рисунке приняты следующие обозначения: передаточная функция эталонной модели; пере даточная функция так называемого адаптивного механизма. • Управление осуществляется основным контуром (Рег. , ОУ, СК), а динамические свойства приближаются к динамическим свойствам эталонной модели. • Существенным недостатком системы является то, что она практически постоянно находится в динамике. Причиной этого является то, что адаптивный механизм имеет большой коэффициент передачи, вследствие чего даже малое отклонение состояния основного контура от состояния эталонной модели приводит к появлению большой величины сигнала на воде ОУ. Для привода, например, это приводит к резкому возрастанию среднего значения тока якоря и, как следствие, росту потребляемой приводом энергии.

• 6. 1. 2. Система с нелинейным регулятором, функциональная схема на рис. 3 ωДв ωЗад БД БУ ЛЧр СПД ωМех • Рис 3. • Где БУ, БД – соответственно блок умножения, блок деления, наличие которых делает систему нелинейной; ЛЧр – линейная часть регуля тора, СПД – система «преобразователь двигатель» ; Мех – механизм. • Предположим имеем нестационарный механизм ( например, в приводе наката суперкаландра отделочного агрегата бумагоделательной машины меняется механическая постоянная привода вследствие изменения момента инерции рулона бумаги). Нестационарность требует постоянной подстройки регулятора скорости, поскольку меняется Краз (Краз коэффициент передачи разомкнутой системы), который при отсутствии нелинейной части регулятора (БД, БУ) , становится переменным.

• Найдем коэффициент передачи разомкнутой системы с учетом нелинейной части: • . Учитывая, что получим • , или • То есть коэффициент передачи разомкнутой системы уже не зависит от переменного коэффициента передачи механизма. Таким образом в данной системе в процессе её функционирования не требуется перестройки регулятора. Система работает как стационарная. Система свободна от недостатков 6. 1. 1, однако по отношению к возмущающему воздействию ведет себя как обычная система

• 6. 1. 1 и 6. 1. 2 относятся к так называемым бес поисковым системам. • 6. 2. Поисковые. • В таких системах в зависимости от изменяющихся динамических свойств объекта управления и возмуща ющих воздействий осуществляется настройка устройства управления, таким образом, чтобы обеспечить оптималь ные свойства системы в целом. • 6. 2. 1 В самонастраивающихся системах в зависимости от изменяющихся условий функционирования произво дится автоматическая коррекция параметров регулятора. • 6. 2. 2 В самоорганизующихся системах осуществля ется коррекция не только параметров, но и структуры (алгоритма управления) системы.

2. Системы подчиненного регулирования. • В процессе управления техническими объектами регулируемая переменная должна наи лучшим образом воспроизводить изменения предписанного значения. При этом часто оказывается необходимым ограничить пределы изменений одной или нескольких промежуточных переменных (например, ток двигателя, его скорость при отработке перемещения и т. п. ). С этой целью одноконтурная система дополняется обратными связями по этим координатам, вступающими в работу, когда контролируемая переменная стремится превысить предельно допустимое значение.

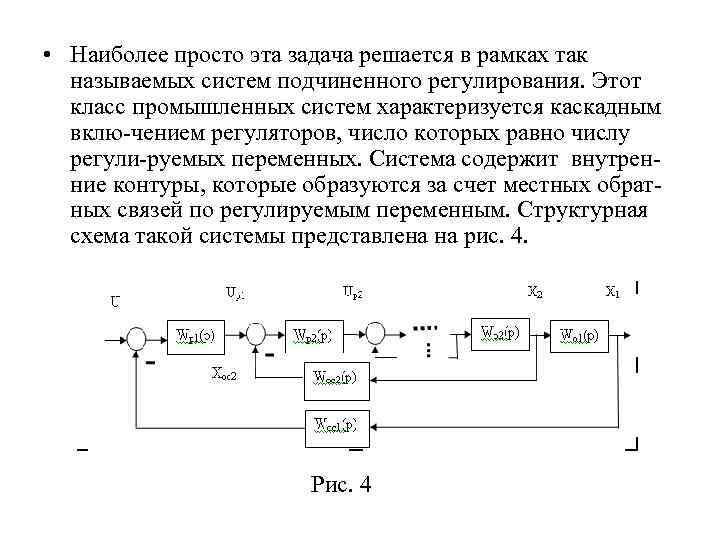• Наиболее просто эта задача решается в рамках так называемых систем подчиненного регулирования. Этот класс промышленных систем характеризуется каскадным вклю чением регуляторов, число которых равно числу регули руемых переменных. Система содержит внутрен ние контуры, которые образуются за счет местных обрат ных связей по регулируемым переменным. Структурная схема такой системы представлена на рис. 4. Рис. 4

• Каждый i ый контур такой системы представляет собой локальную САУ. Задающим воздействием для i го контура является Upi 1 сигнал с выхода регулятора (i 1) го контура , иными словами i ый (внутренний) контур подчинен (i 1) – му (внешнему) контуру. При известном коэффициенте передачи i го контура установившееся значение переменной на выходе его будет ограничено, если ограничить сигнал на выходе (i 1) го регулятора. При таком способе ограничения переменной максимальное значение её может быть превышено на малое время при скачкообразном изменении сигнала на входе контура.

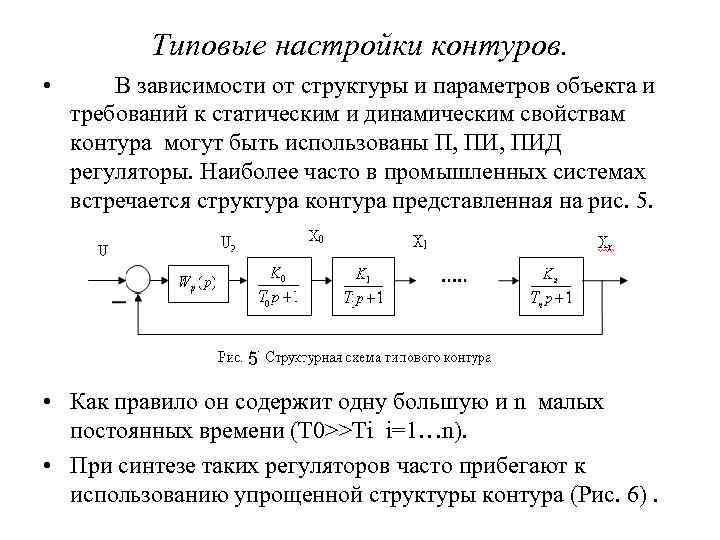Типовые настройки контуров. • В зависимости от структуры и параметров объекта и требований к статическим и динамическим свойствам контура могут быть использованы П, ПИД регуляторы. Наиболее часто в промышленных системах встречается структура контура представленная на рис. 5. 5 • Как правило он содержит одну большую и n малых постоянных времени (Т 0>>Ti i=1…n). • При синтезе таких регуляторов часто прибегают к использованию упрощенной структуры контура (Рис. 6).

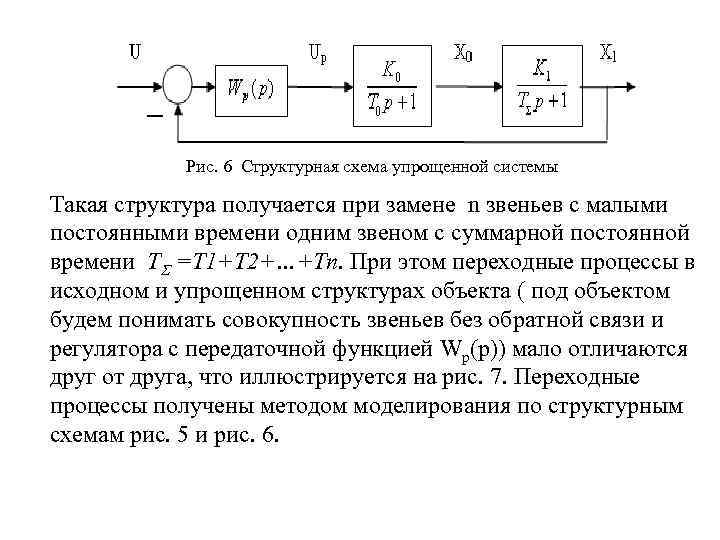Рис. 6 Структурная схема упрощенной системы Такая структура получается при замене n звеньев с малыми постоянными времени одним звеном с суммарной постоянной времени ТΣ =Т 1+Т 2+…+Тn. При этом переходные процессы в исходном и упрощенном структурах объекта ( под объектом будем понимать совокупность звеньев без обратной связи и регулятора с передаточной функцией Wр(р)) мало отличаются друг от друга, что иллюстрируется на рис. 7. Переходные процессы получены методом моделирования по структурным схемам рис. 5 и рис. 6.

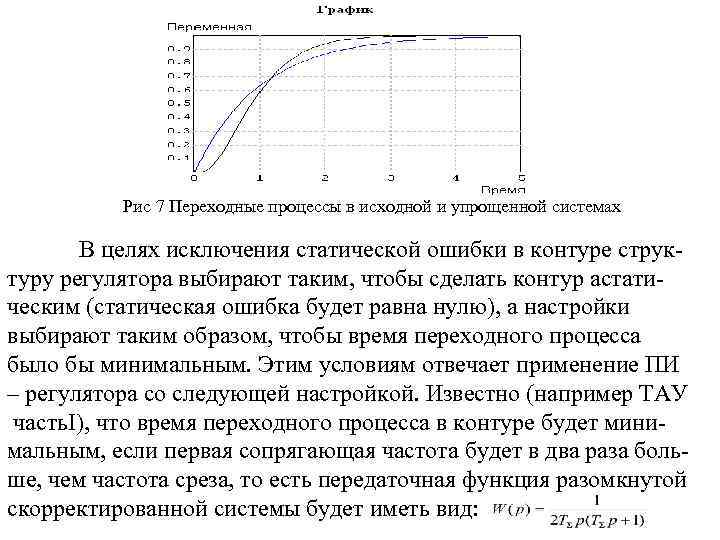Рис 7 Переходные процессы в исходной и упрощенной системах В целях исключения статической ошибки в контуре струк туру регулятора выбирают таким, чтобы сделать контур астати ческим (статическая ошибка будет равна нулю), а настройки выбирают таким образом, чтобы время переходного процесса было бы минимальным. Этим условиям отвечает применение ПИ – регулятора со следующей настройкой. Известно (например ТАУ часть. I), что время переходного процесса в контуре будет мини мальным, если первая сопрягающая частота будет в два раза боль ше, чем частота среза, то есть передаточная функция разомкнутой скорректированной системы будет иметь вид:

• Этого можно достигнуть при τ=T 0 , Kраз= , откуда. Получили типовую, так называемую, настройку на оптимум по модулю (ОМ). • Найдем передаточную функцию замкнутой системы. • • где А, как известно, при такой структуре и таких параметрах переходные процессы в замкнутой системе будут иметь минимальное время переходного процесса, а перерегулирование σ<5%.

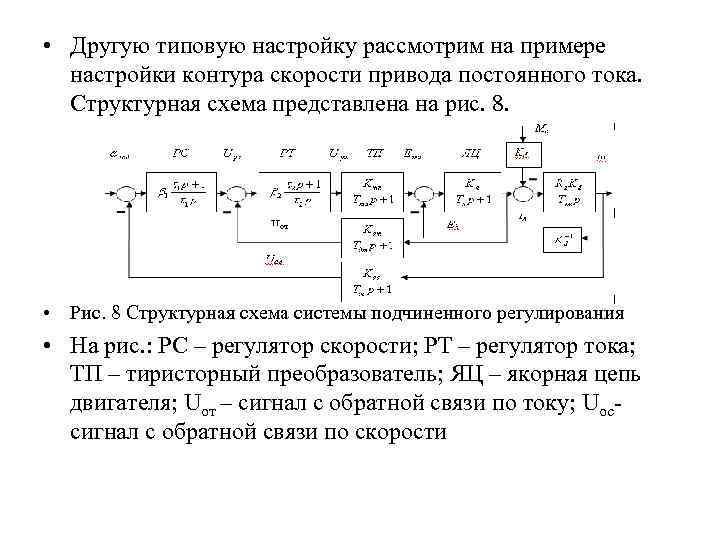• Другую типовую настройку рассмотрим на примере настройки контура скорости привода постоянного тока. Структурная схема представлена на рис. 8. • Рис. 8 Структурная схема системы подчиненного регулирования • На рис. : РС – регулятор скорости; РТ – регулятор тока; ТП – тиристорный преобразователь; ЯЦ – якорная цепь двигателя; Uот – сигнал с обратной связи по току; Uос сигнал с обратной связи по скорости

• Система содержит два контура: контур тока, предназначен ный для регулирования тока якоря и ограничения максимального значен 6 ия тока; контур скорости для управления скоростью двигателя. Выход регулятора скорости фактически является задатчиком для контура тока. Иными словами: «контур тока подчинен контуру скорости» . Контура оказываются связанными между собой посредст вом внутренней обратной связи двигателя по ЭДС Ед. Однако в подавляющем большинстве случаев действием этой связи в динамике можно пренебречь, поскольку Ед меняется значительно медленней, чем ЭДС тиристорного преобразователя (Етп), таким образом можно считать контура независимыми, что позволяет решать задачу синтеза регулятора этих контуров как в самостоятельной системе

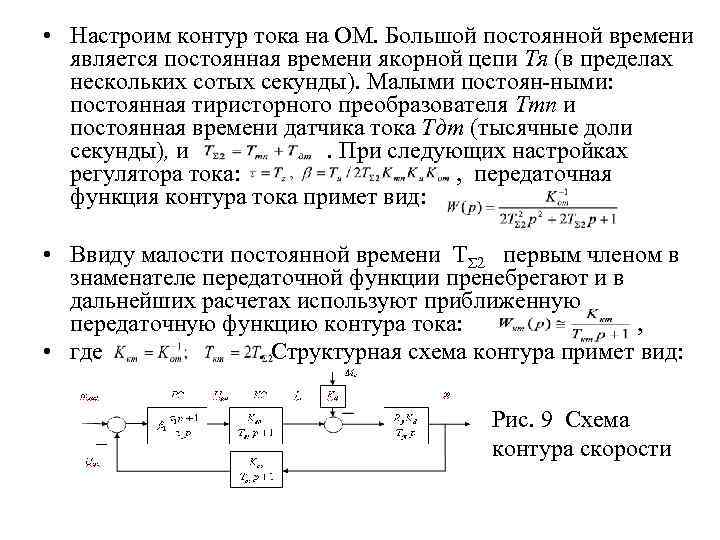• Настроим контур тока на ОМ. Большой постоянной времени является постоянная времени якорной цепи Тя (в пределах нескольких сотых секунды). Малыми постоян ными: постоянная тиристорного преобразователя Ттп и постоянная времени датчика тока Тдт (тысячные доли секунды), и. При следующих настройках регулятора тока: , передаточная функция контура тока примет вид: • Ввиду малости постоянной времени ТΣ 2 первым членом в знаменателе передаточной функции пренебрегают и в дальнейших расчетах используют приближенную передаточную функцию контура тока: , • где. Структурная схема контура примет вид: Рис. 9 Схема контура скорости

• При настройке контура скорости возможны следующие варианты: ПИ – регулятор с настройкой на ОМ; П регулятор с настрой кой на ОМ; ПИ – регу лятор с настройкой на симметричный оптимум (СО). • С настройкой на ОМ мы познакомились выше. Однако, в этом случае она имеет свои особенности. Это то, что контур вместо апериодического содержит интегрирующее звено. Передаточная функция разомкнутой системы при настойках, рассмотренных выше будет иметь вид: • . Передаточная функция имеет в знаменателе р2, то есть ЛАХ будет содержать начальный участок с наклоном 40 дец/дек. Вид ЛАХ представлен на рис. 10

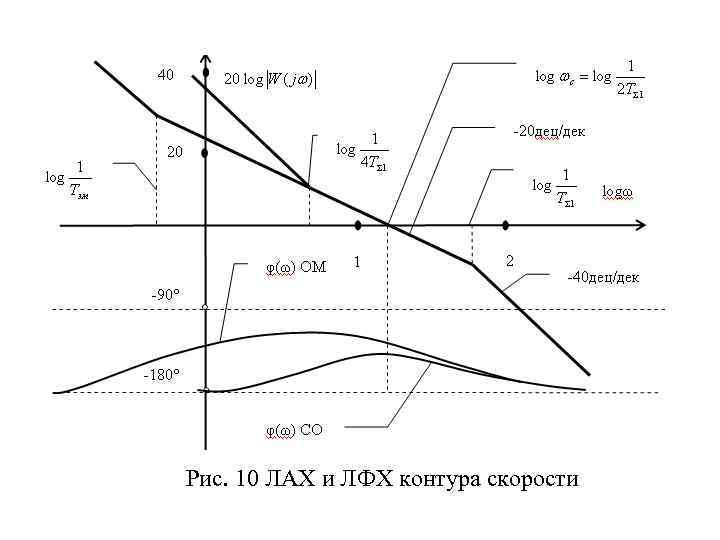Рис. 10 ЛАХ и ЛФХ контура скорости

• Если Тэм достаточно велико (первая сопрягающая частота смещается в сторону низких частот), то числитель можно приближенно представить как Тэм р и передаточная функция становится такой же как и в предыдущем случае, а соответственно и динамика системы буде приближаться к рассмотренной выше Предположим τ < Тэм , заметим при этом , что с уменьшением τ растет коэффициент передачи разомкнутой системы на низких частотах, а это как известно приводит к повышению точности, однако уменьшается запас по фазе и процесс в замкнутой системе становится более колебательным. Для случая τ

• Система с П – регулятором обладает высоким быстро действием, однако изменение момента сопротивления приводит к появлению статической ошибки, что может оказаться недопустимым по условиям заданного течения технологического процесса, обеспечиваемого приводом (рис. 11 а) • Настройка на СО обеспечивает наименьшее отклонение скорости при действии возмущений. Обычно настройка на СО используется в системах стабилизации скорости с большими периодами смены режима течения технологического процесса. Настройка на ОМ с ПИ регулятором применяется в приводах в системах, где недопустимо наличие статической ошибки и достаточно часто меняется скорость привода. Времена переходного процесса для нашего примера для СО и ОМ с ПИ – регулятором приблизительно равны. • Минимальное перерегулирование в системе с ОМ и П – рег. (σ=4. 5 … 4. 8%), в системе ОМ с ПИ – рег. в данном конкретном случаеσ =21 … 22%, в системе с СО σ=43%.

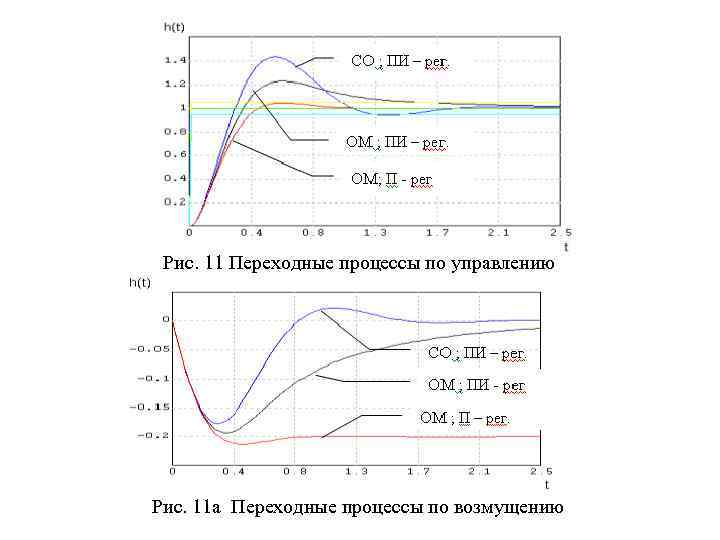Рис. 11 Переходные процессы по управлению Рис. 11 а Переходные процессы по возмущению

Выбор и расчет элементов регуляторов и обратных связей • При проектировании систем подчиненного регулирования заключительным этапом является этап выбора и расчета элементов регуляторов и обратных связей. • Для технической реализации устройств формирования управляющих воздействий используются, как правило, операционные усилители. На рис. 12 приведена схема контура тока на основе которой рассчитаем параметры элементов ПИ регулятора тока (Rот, С, Rзт, Rт), и элементов обратной связи (Rш, Rфт, Сфт). Определим параметры схемы контура тока. Сопротивления Rот, Rзт определяются из условия Rот/ Rзт=β 2, при этом следует принять: Rот=1 ком, Rзт > 1 ком, если β 2<1 Rот>1 ком, Rзт = 1 ком, при β 2>1.

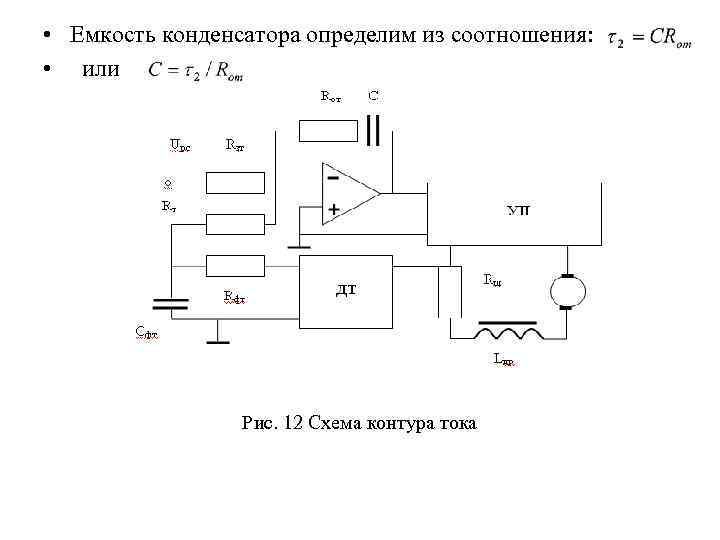• Емкость конденсатора определим из соотношения: • или Рис. 12 Схема контура тока

• Поскольку коэффициент передачи контура тока равен , то при максимальном напряжении на выходе регу лятора скорости (в аналоговых системах Uрс max=10 в) Iя max=10*К-1 ос, откуда получим Кос=10 / Iя max. Этот коэф фициент образуется следующими элементами обратной связи: падением напряжения на сопротивлении шунта Rш, усилителем датчика тока (ДТ) Кдт, Сопротивлением фильтра обратной связи по току Rфт и сопротивлением на входе регулятора Rт. Кот= Rш Кдт Кт или , Кт= Кот / (Rш Кдт) где Кт – коэффициент приведения обратной связи по току к задающему входу. С другой стороны Кт=Rзт /(Rт+ Rфт) или Rт+ Rфт= Rзт/Кт. Из последнего соотношения определяется сумма сопротивлений Rт+ Rфт , из которой выделяем Rт и Rфт. Далее из равенства Тос= C Rфт определяем величину емкости конденсатора С.

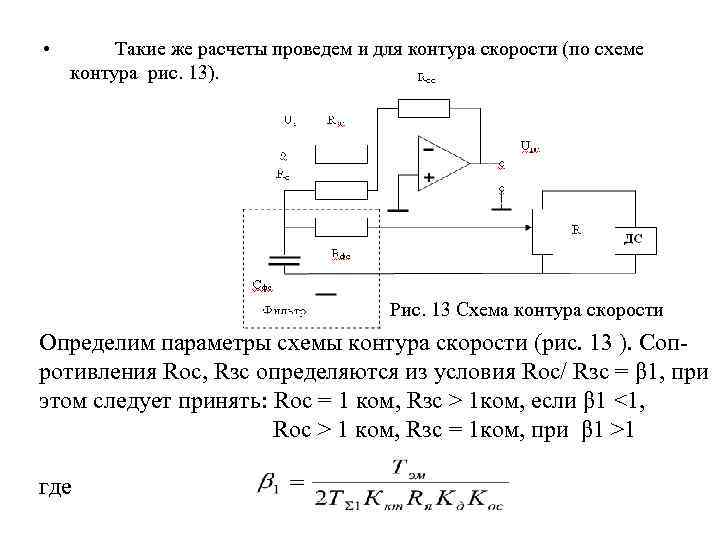• Такие же расчеты проведем и для контура скорости (по схеме контура рис. 13). Рис. 13 Схема контура скорости Определим параметры схемы контура скорости (рис. 13 ). Соп ротивления Rос, Rзс определяются из условия Rос/ Rзс = β 1, при этом следует принять: Rос = 1 ком, Rзс > 1 ком, если β 1 <1, Rос > 1 ком, Rзс = 1 ком, при β 1 >1 где

• Поскольку коэффициент передачи контура скорости равен , то при максимальном напряжении на входе системы (в аналоговых системах Uрс max=10 в) ωн=10*К-1 ос, откуда получим Кос=10 / ωн. Этот коэффициент образуется следующими элементами обратной связи: напряжением на зажимах тахогенератора Uтг; делителем R (коэффициент передачи делителя КR может меняться в пределах 0… 1); фильтром в обратной связи по скорости Rфс и Сфс ; сопротивлением на входе регулятора Rс. Тогда Кос = Ктг КR Кс или , Кс = Кос / (КR Ктг) (Кс – коэффициент приведения обратной связи по скорости к задающему входу). С другой стороны Кс=Rзс / (Rс+Rфc), из этого соотношения и определим Rc. • Статическую регулировочную характеристику тахогенератора Uтг=f(ω) можно считать линейной, а его коэффициент передачи Ктг=0, 03 Uтг /π. Технические данные тахогенераторов данные можно найти в справочниках.

3. Синтез следящих систем • Одним из основных требований, предъявляемых к качественным показателям следящих систем (СС) является «точность воспроизведения входного сигнала» . Остальные требования, как правило, рассматриваются как ограничения: • , • где Q ошибка, tпп время переходного процесса, σ перерегулирование. • Как было показано в дисциплине ТАУ, точность системы определяется видом низкочастотной части ЛАХ. Поэтому при решении задачи синтеза в целях обеспечения заданной точности СС формируют её специальным образом.

• • • При использовании метода ЛЧХ последовательность решения задачи следующая: 1) Строим ЛАХ разомкнутой нескорректированной системы (Lнк), предварительно приведя ее к одноконтурной; 2) Строим желаемую ЛАХ (Lж) исходя из требований предъявляемых к системе; ЛАХ регулятора (Lрег) получаем путем вычитания ЛАХ нескорректированной из ЛАХ желаемой. По Lрег получаем структуру и параметры регулятора. Низкочастотная часть ЛАХ строится таким образом, чтобы обеспечить точность отработки входного воздействия при его известных предельных параметрах: максимальной скорости , максимальном ускорении и допустимой ошибке слежения.

• Закон изменения входного сигнала удобно представить в виде некоторого эквивалентного гармонического воздействия с заданными предельными характеристиками: Тогда , где (3. 1) , где (3. 2) Из (3. 1) и (3. 2) можно получить : (3. 3) • • • При оценке точности проектируемой системы, например методом моделирования, на входе ее следует сформиро вать именно это воздействие

• Полученные параметры эквивалентного воздействия используются для построения так называемой «запретной зоны» . Доказано, что ошибка слежения не будет превы шена если ЛАХ системы пройдет выше запретной зоны (см рис. 14). Рис. 14 Запретная зона

• Желаемую ЛАХ будем строить приближенным методом. при построении которой необходимо руководствоваться следующими соображениями: • 1) в низкочастотной части она не должна пересекать запретную зону • 2) в среднечастотной части • она должна пересекать ось 0 дец с наклоном 20 дец/дек (на частоте среза ); • протяженность среднечастотной области по возможнос ти должна быть как можно продолжительной. Обеспече ние этого условия позволяет минимально возможную колебательность в системе. • 3) Высокочастотная часть ЛАХ практически не оказывает влияния на динамику системы при условии, что , где ωсопр сопрягающая частота ближайшая справа к частоте среза.

• Рассмотрим решение задачи на конкретном примере. • Предположим, следящая система строится по принципу подчиненного регулирования и содержит 3 контура: контур тока (КТ); контур скорости (КС); контур положения (КП). Контур тока настроен на ОМ, в контуре скорости используется П – регулятор, фильтры в обратных связях по току и скорости отсутствуют. При этих условиях передаточная функция контура скорости примет вид: • • , • где Ккс=Кос-1; ; ξ=0. 707 • Структурная схема системы представлена на рис. 15.

Рис. 15 Структурная схема следящей системы • Где Q – ошибка (Q=Qзад Qвых); Uрп – управляющее воздействие с выхода регулятора положения; ω – угловая скорость двигателя. • Необходимо найти структуру и параметры регулятора при следующих исходных данных: Кkc=К=10. 53; Ткс =0. 009; Qmax= 0. 013 - максимальная ошибка слежения Ωmax 0. 67 максимальная скорость εmax= 0. 5 максимальное ускорение

• Построим запретную область • • • Вычисли добротность системы по скорости : • Определим коэффициент усиления регулятора из следующего выражения: , тогда Сопрягающая частота для колебательного звена: ω3=1/Tкс=1/0. 009=111, 1,

• Порядок построения желаемой ЛАХ • 1. Строим запретную зону, используя следующие данные • 2. Строим ЛАХ нескорректированной системы L(0)=20 log. KКред и сопрягающая частота ω=ω3. • 3. Сопрягающую частоту выбираем таким образом, чтобы среднечастотный участок желаемой ЛАХ был симметричным относительно частоты среза, а сопрягающую частоту справа от частоты среза принимаем равной ω3. • Все вышесказанное иллюстрируется на рис. 16. • Низкочастотные части нескорректированной и желаемой ЛАХ сливаются с границей запрет ной зоны. ЛАХ регулятора получается простым вычитанием Lрег=Lж Lнк

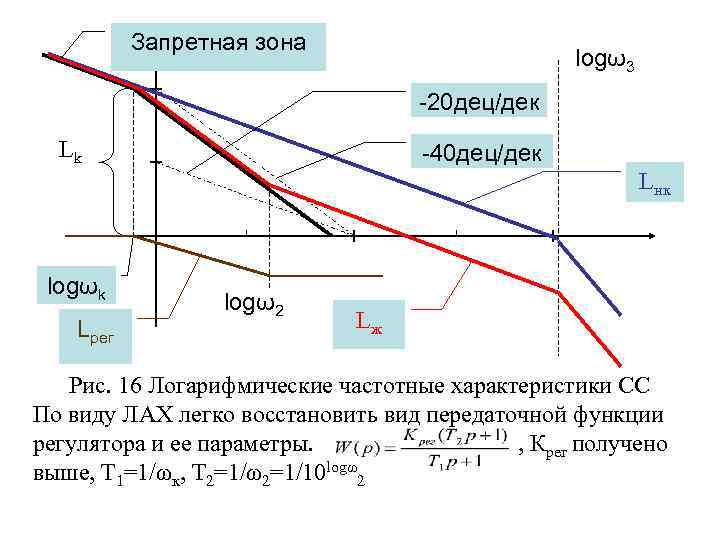Запретная зона logω3 -20 дец/дек Lk -40 дец/дек Lнк logωk Lрег logω2 Lж Рис. 16 Логарифмические частотные характеристики СС По виду ЛАХ легко восстановить вид передаточной функции регулятора и ее параметры. , Крег получено выше, Т 1=1/ωк, Т 2=1/ω2=1/10 logω2

• По ЛАХ регулятора получим структуру и пара метры регулятора. Регулятор имеет 2 сопрягаю щие частоты ωк и ω2. При этих сопрягающих частотах ЛАХ меняет наклон на 20 дец/дек (это говорит о том, что регулятор содержит 2 звена первого порядка: одно в знаменателе (на частоте ωк наклон меняется на – 20 дец/дек) и одно в чис лителе (на частоте ω2 наклон меняется на +20 дец/дек). Таким образом передаточная функция регулятора будет иметь вид • Крег получено выше, Т 1=1/ωк, Т 2=1/ω2=1/10 logω2

4. Позиционная система • Напомним, что позиционная система предназначена для перевода объекта из произвольного начального состояния в конечное, за минимально возможное время, с заданной степенью точности. • Для промышленных автоматических ЭМС оптимальными условия ми перемещения из исходного в заданное состояние будут: 1) разгон до максимальной скорости с максимальным ускорением; 2) движение с максимальной скоростью; 3) торможение с максимальным ускоре нием. Выполнение этих требований для больших перемещений при водит к так называемому трпециедальному графику изменения ско рости, при средних перемещениях к треугольному. Это позволяет в полной мере использовать перегрузочные способности двигателя и исключает возможности перерегулирования по положению. максимальной скоростью.

• В режиме малых перемещений ни один из регуляторов не достигает насыщения. Участки движения с максимальным током и тем более с максимальной скоростью отсутствуют, система функционирует как линейная. • В режиме средних перемещений регулятор скорости достигает насыщения, на траектории движения механизма присутствует участок с максимальным током. • В режиме больших перемещений график изменения скорости трапециидальный, на траектории присутствуют участки, где регуляторы положения и скорости достигают насыщения, система движется либо с максимальным ускорением, либо

На рис. 17 приведены графики изменения переменных состояния в позиционной системе в режиме больших перемещений Рис. 17 Рассмотрим позиционную трехконтурную систему с П регу-лятором в контуре скорости. Близкий к указанному график обеспечивает так называемый параболический регулятор в контуре положения, для которого заданная скорость движения механизма формируется по закону: Структурная схема такой системы представлена на рис. 18

Рис. 18 Структурная схема системы с параболическим регулятором По своей сути регулятор положения представляет собой безынерционное звено с переменным коэффициентом передачи. По мере приближения к конечной точке траектории, то есть при стремлении ошибки ε к нулю коэффициент передачи регулятора стремится к ∞, В следствии этого в системе возникают автоколе бания с достаточно малой амплитудой по положению и значитель ной по току, причем амплитуда колебаний по току зависит от коэффициента передачи линейной части регулятора положения Крп. В результате в этой точке возникает момент, удерживающий механизм заданном положении.

• Коэффициент передачи регулятора предварительно можно определить из следующего соотношения: • • Окончательное значение устанавливается либо в процессе исследования системы методом моделирования, либо при наладке и настройке реальной позиционной системы • Нелинейности на выходах регулятора скорости и положения предназначены для ограничения максималь ного значения соответственно тока якоря и скорости. • Как видно из вышеизложенного позиционная система является типичным представителем нелинейных систем, где основные нелинейности введены в систему искусственно.

5. 1 Инвариантная система стабилизации скорости • Одной из основных причин, вызывающих отклонение состояния системы от заданного, являются внешние воз мущающие воздействия. С целью уменьшения этих откло нений, а в идеальном случае исключения такого отклоне ния, строят системы с регулированием по возмущению или инвариантные системы. • Теория инвариантных систем является одним из основных разделов общей теории автоматического управления, в которой решаются задачи синтеза структуры и параметров САУ, находящейся под воздействием внешних возмуще ний и помех. • При выполнении условий инвариантности в идеальном случае достигается полная независимость (абсолютная инвариантность) управляемой переменной состояния от внешнего возмущающего воздействия.

• Для достижения абсолютной инвариантности некоторой переменной состояния Xi(t) относительно внешнего возмущающего воздействия fi(p) необходимо и достаточно чтобы передаточная функция W(p)=Xi(p)/fi(p) была тождественно равна нулю. Реализовать это условие можно, если W(p) представить в виде разности не менее двух передаточных функ ций. (p)=W 1(p)-W 2(p) W • Тогда критерий реализуемости абсолютной инвариантности системы можно сформулировать следую щим образом: для физической реализуемости абсолютной инвариантности САУ необходимо в её структуре наличие не менее двух каналов передачи возмущающего воздейст вия между точкой его приложения и точкой, относительно которой достигается условие инвариантности. • Для систем стабилизации скорости электропривода основным возмущающим воздействием является изменение момента сопротивления нагрузки Мс.

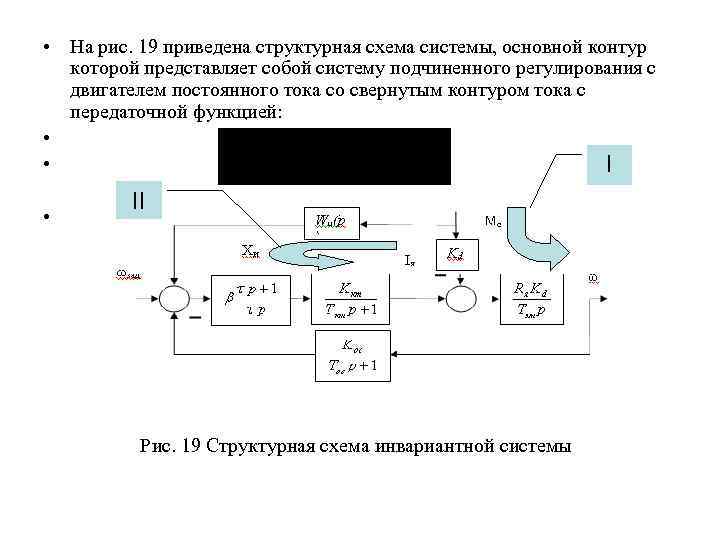• На рис. 19 приведена структурная схема системы, основной контур которой представляет собой систему подчиненного регулирования с двигателем постоянного тока со свернутым контуром тока с передаточной функцией: • • I • II Рис. 19 Структурная схема инвариантной системы

• Основным возмущающим воздействием является изменение момента сопротивления на валу двигателя (Мс). Основной канал распространения возмущения с передаточной функцией (на рис. 15 стрелка I): Дополнительный канал, обеспечивающий инвариантность сис темы по отношению к возмущению с передаточной функцией: На рис. 19 стрелка II, так же рис. 20. Рис. 20 Искусственный канал распространения возмущения

• Из условия: W(p)=W 1(p)-W 2(p)=0 получим: • • По известным причинам техническая реализация устройст ва в аналоговом варианте с такой передаточной функцией невозможна. Сопрягающая частота лежит в области , близ кой к области малых параметров, то есть звено оказывает меньшее влияние на динамику системы в целом и им можно пренебречь. Окончательно для технической реализации системы передаточную функцию примем в виде: • • где • При этом, как показало исследование такой системы, параметры , рассчитанные по полученным формулам являются оптимальными для рассматриваемого случая.

5. 2 Грубые системы с жесткой структурой регулятора • Непосредственно к адаптивным и инвариантным системам примыкают так называемые грубые системы, то есть системы обладающие малой чувствительностью к вариациям параметров объекта управления и регулятора. • Под чувствительностью понимают степень влияния изменения параметров системы управления на ее свойства, и в первую очередь на критерий оценки качества системы. • Адаптивные системы, например системы с эталонной моделью, позволяют скомпенсировать влияние как внешних, . так и внутренних возмущений, инвариантные скомпенсировать влияние внешних. Каждая из этих систем имеет свои преимущества и недостатки, о которых сказано выше.

• В большинстве случаев требования к системе формулируются как обеспечение не оптимального значения критерия качества, а обеспечение величины близкой к некоторой заданной с запасом на параметрические и внешние возмущения. Очевидно, эти свойства могут быть удовлетворены в системах с различными принципами построения, и задача синтеза уже решается не как задача оптимизации, а задача выбора наилучшего среди альтернативных вариантов с учетом дополнительных требований, например экономических. С учетом сказанного среди уже рассмотренных принципов построения может занять грубая система с жесткой структурой регулятора. • Рассмотрим обобщенную структуру системы управления приведенную на рис 21. К такой структуре можно свести подавляющее большинство промышленных систем.

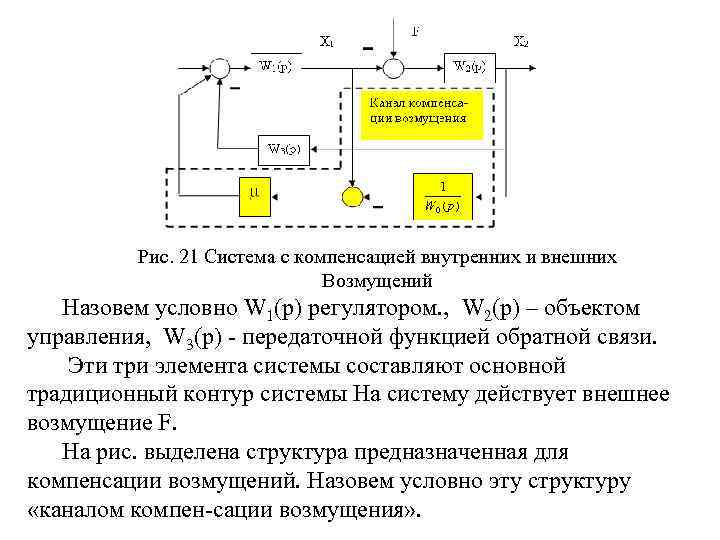Рис. 21 Система с компенсацией внутренних и внешних Возмущений Назовем условно W 1(p) регулятором. , W 2(p) – объектом управления, W 3(p) передаточной функцией обратной связи. Эти три элемента системы составляют основной традиционный контур системы На систему действует внешнее возмущение F. На рис. выделена структура предназначенная для компенсации возмущений. Назовем условно эту структуру «каналом компен сации возмущения» .

• Передаточная функция при функционировании системы меняется на величину ΔW по отношению к расчетной W 20, то есть текущая передаточная функция объекта управления W 2= W 20+ ΔW. ΔW и будет являться внутренним возмущением. Очевидно, отклонение выходной переменной от заданного значения будет зависеть как от внешнего, так и внутреннего возмущения. Текущее значение выходной переменной • X 2=(X 1 F)(W 20+ ΔW) (8. 1) • Предположим, что совокупность внешних и внутренних возмущений образует некоторое суммарное возмущение FΣ, тогда • Х 2= (X 1 F)(W 20+ ΔW)=(Х 1 FΣ)W 20 (8. 2)

• Из последнего выражения можно получить значение суммарного возмущения • FΣ=F+(F X 1)ΔW/W 20, которое состоит из внешнего F и внутреннего возмущения • Fвн=(F X 1) ΔW/ W 20. • Из (8. 2) следует, что Х 2=(Х 1 FΣ)W 20. • Это равенство позволяет оценить суммарное возмущение: • FΣ=X 1 X 2/ W 20 • Коэффициент усиления в канале компенсации µ рассчитывается из условия отсутствия перекомпенсации внешнего возмущения в статике во всем диапазоне изменения параметров объекта.

6. Система с модальным регулятором • Известно, что динамические свойства линейных стационарных системы определяются распределением корней характеристического уравнения на плоскости комплексного переменного. • Модальное управление (модальный регулятор) и обеспечивает заданное распределение полюсов (корней характеристического уравнения или собственных чисел матрицы системы) с целью достижения требуемых дина мических свойств системы. Положение полюсов обеспе чивается регулятором, который формирует линейную ком бинацию переменных состояния системы. Очевидно, что модальный регулятор предполагает наличие полного век тора состояния. В современных системах требование наличия полного вектора состояния не является жестким ограничением, поскольку при необходимости его недостающие составляющие можно восстановить при помощи технического устройства, называемого идентифи катором состояния.

• Рассмотрим решение задачи синтеза модального регулятора. • Известными методами представим модель объекта в виде уравнений состояния • Будем искать управление в виде , где вектор коэффициентов обратных связей, т знак транс понирования, входное воздействие на систему. При этом предполагается, что коэффициенты передачи датчиков, измеряющих переменные состояния, входят в вектор. Тогда уравнение динамики системы примет вид: • (5. 1) • желаемая матрица системы с модальным регулятором. • При известных матрицах А и В, задав определенным образом проекции вектора , можно обеспечить заданное распределение корней, а вместе с этим и заданные динами ческие свойства системы в целом.

• Существуют уравнения, со стандартным распределением корней на плоскости комплексного переменного. Например, биномиальное распределение , при котором в системе обеспечиваются апериодические переходные про цессы. Численные значения ω0 определяют быстродействие синтезируемой системы. Каждому виду стандартной формы соответствует определенный вид переходного процесса. • Вычисление параметров регулятора осуществляется следующим образом: • Находим коэффициенты характеристического уравнения, в общем случае по известным правилам • Приравниваем коэффициенты полученного уравнения, которые являются функциями искомых коэффициентов обратных связей, соответствующим коэффициентам задан ной стандартной формы. В результате получаем систему алгебраических уравнений. Решаем полученную систему алгебраических уравнений относительно неизвестных коэффициентов ki.

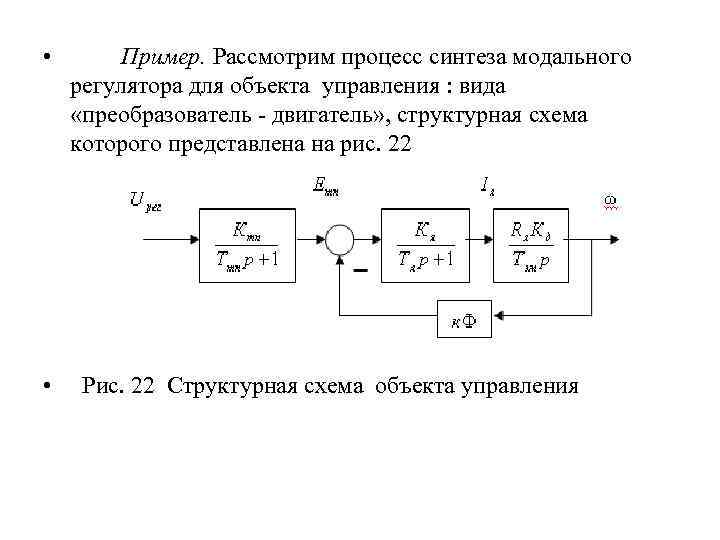• • Пример. Рассмотрим процесс синтеза модального регулятора для объекта управления : вида «преобразователь двигатель» , структурная схема которого представлена на рис. 22 Рис. 22 Структурная схема объекта управления

• С учетом (5. 1) вид желаемой системы дифференциальных уравнений примет вид: • или • Представим эту систему в векторно – матричном виде: • , где матрица А имеет вид:

• Характеристическое уравнение системы : • Где Для систем третьего порядка наиболее часто используют следующие стандартные формы: Биномиальное распределение Распределение Баттерворта Распределение вида Например для биномиального распределения следует принять:

• В результате получим систему трех алгебраических уравнений с тремя неизвестными, решая которую получим численные значения коэффициентов жестких обратных связей k 1, k 2, k 3. В частном случае для нашей системы коэффициент главной обратной связи по скорости (Кос) определяет коэффициент передачи привода в целом. Для соблюдения этого условия представим коэффициент в виде k 3=Kocку, где ку, коэффициент усиления безынерционного усилителя, включенного последовательно с силовым преобразователем в прямую цепь системы, тогда имеем: • kу=k 3/Koc, K 1=k 1/kу, K 2=k 2/kу. • Эти параметры должны быть установлены в реальной системе.

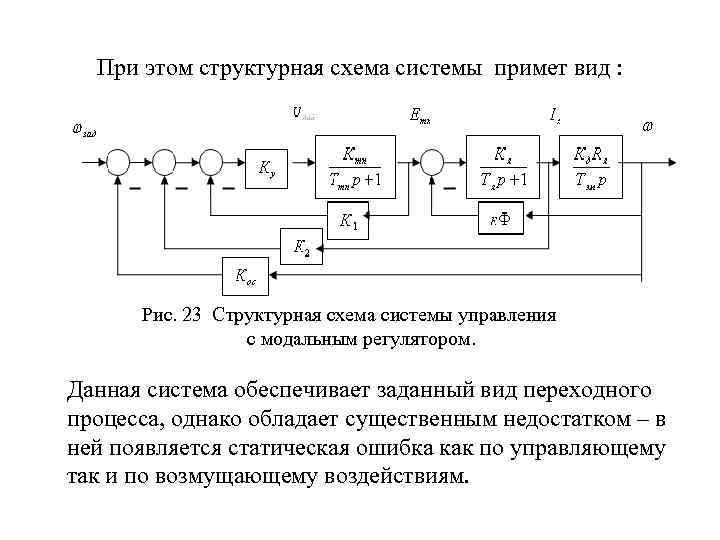При этом структурная схема системы примет вид : Рис. 23 Структурная схема системы управления с модальным регулятором. Данная система обеспечивает заданный вид переходного процесса, однако обладает существенным недостатком – в ней появляется статическая ошибка как по управляющему так и по возмущающему воздействиям.

7. Аналитическое конструирование регуляторов • В большинстве случаев приходится решать задачу оценки точности системы не в какой либо конкретной точ ке времени и пространства, а на каком либо пространст венном или временном интервале. Это либо максимальная (ε max) на этом интервале, либо средняя (J=ε ср) ошибка: • Интегральные оценки можно использовать и для оценки переходной функции (h(t)). Интегральная оценка вида: • (S – заштрихованная площадь ) может говорить о качестве лишь при условии монотонности процесса. Чем больше площадь S, (больше значение интегра ла), тем больше время переходного процесса, тем меньше средняя величина отклонения от установившегося значения.

• Наибольшее распространение при решении задач оценки качества систем их синтеза (например, задачи аналитического конструирования регуляторов) получили так называемые интегральные квадратич-ные оценки. Как правило на их основе оценивается способность системы сохранять заданное состояние. • В системе n го порядка в каждый текущий момент времени ее состояние (Х) должно соответствовать величине (Хзад заданному состоянию). Однако, наличие возмущений Z вызывает отклонение состояния системы (∆Х) от заданного ∆Х=Хзад Х. • Интегральную оценку такого отклонения получают на основе так называемых интегральных квадратичных форм где симметричная матрица весовых коэффициентов, поз воляющая учесть вклад каждой составляющей ΔХi в вели чину критерия J.

• Если принять диагональной, то подынтегральное выражение получим в виде: • То есть имеем взвешенную сумму квадратов отклонений от заданного состояния. Коэффициенты βii играют роль весовых коэффициентов и позволяют регулировать величину вклада в показатель отклонения той или иной переменной состояния. Окончательно имеем: • Можно показать, что положение минимума средней ошибки и интегральной квадратичной формы совпадают.

• Задача поиска экстремума критерия приведенного выше вида, то есть задача оптимизации системы по этому критерию носит название линейно – квадратичной задачи. При этом известно, что линейно квадратичная задача является единственной, при которой решение получается в общем виде. Это решение находит практическое применение при проектировании САУ при многомерной линейной модели в приращениях. В современной литературе методы решения таких задач получили название «Аналитическое конструирование оптимальных регуляторов» (АКОР). Впервые этот термин использовал в своих работах советский ученый Лётов. Одним из таких методов является метод синтеза по «Критерию обобщенной работы» , автором которого является Красовский А. А. , которым доказана следующая теорема.

• Для линейной стационарной системы вида, динамика которой описывается системой дифференциальных уравнений вида оптимальным в смысле минимума функционала: является управление где L симметричная матрица, которая является решением мат ричного алгебраического уравнения ; А – матрица объекта управления размерностью n*n; В – матрица чувстви тельности объекта к управляющим воздействиям размерность которого n*m; вектор отклонений переменных состояния объекта от заданного состояния; β симметричная матрица весовых коэффициентов; К 2 диагональная матрица коэффициентов передачи безынер ционных усилителей по i му управляющему воздействию (i=1, 2…m).

• Первая составляющая функционала представляет квадратичную форму отклонений переменных состояния от заданного состояния, Вторая составляющая носит название «обобщенной взвешенной работы управления» , третья «обобщенной работы сигналов управления» . Фактически вторая и третья составляющие характеризуют затраты энергии на управление. В целом решение задачи поиска минимума такого функционала представляет собой поиск компромисса между точностью поддержания состояния и затратами энергии на управление. • При решении задачи осуществляется поиск такой матрицы β, которая в результате решения матричного уравнения обеспечила бы требуемые свойства системы в целом.

• Предположим, в системе имеется два управляющих воздействия (управления задаются на первый и к й входы объекта управления). В этом случае ненулевыми в В будут только первый и к й столбец, тогда вектор управляющих воздействий согласно теоремы После выполнения операции умножения будем иметь:

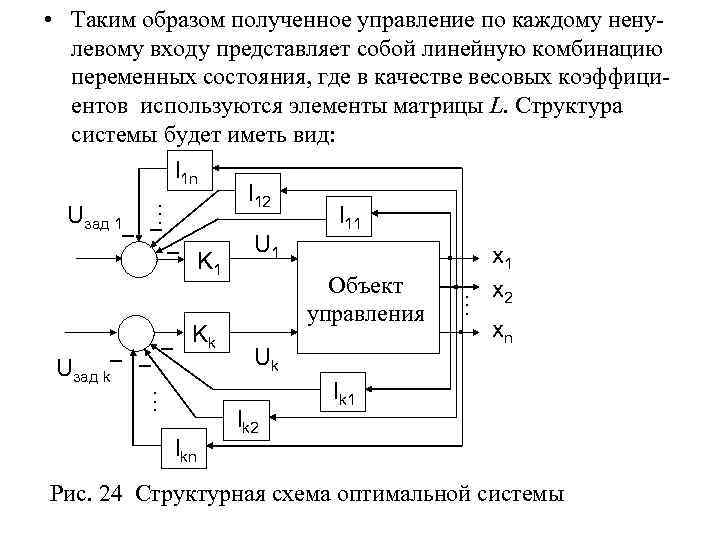• Таким образом полученное управление по каждому нену левому входу представляет собой линейную комбинацию переменных состояния, где в качестве весовых коэффици ентов используются элементы матрицы L. Структура системы будет иметь вид: l 1 n l 12. . Uзад 1. l 11 U 1 x 1 K 1 Объект. x 2. . управления xn Kk Uk Uзад k. lk 1. . lk 2 lkn . . . Рис. 24 Структурная схема оптимальной системы

• Пример. В качестве объекта управления примем систему “преобразователь двигатель” с замкнутым контуром тока, настроенном на оптимум по модулю. Прямое построение системы с управлением вида в общем случае по возмущающему воздействию приведет к статической системе, а соответственно к появлению статической ошибки. Введем дополнительную псевдопеременную Х 3, которая представляет собой интеграл от ошибки: • , • что соответствует интегрирующему звену с передаточной функцией W 0(p)=K 0 /p. С учетом этого построим структурную схему оптимальной системы. Рис. 24 Структурная схема оптимальной системы

• Рассмотрим передаточную функцию участка цепи, которую образуют параллельно включенные звенья • , где • Таким образом введение псевдопеременной Х 3 идентично использованию ПИ – регулятора. • Объект управления включает три звена, обозначив отклонения от заданного состояния (приращения) c учетом того, что , получим следующую систему дифференциальных уравнений:

• Матрица А системы имеет следующий вид: Где Матрица В представляет собой матрицу столбец:

• В работах Красовского показано, что синтезированная по матрице А, имеющей нулевые или положительные собственные числа, может быть неустойчивой. Мы имеем как раз матрицу А, которая имеет два нулевых собственных числа. Для таких объектов авторами метода рекомендован так называемый метод нестационарного функционала. Все переменные состояния в таком функционале умножаются на экспоненту вида • • где носит название времени релаксации функционала. Матрица А, соответствующая новым переменным, может быть получена следующим образом:

• Решим уравнение диагональной или: приняв матрицу ß + Решение матричного алгебраического уравнения можно свести к решению системы алгебраических уравнений, приравнивая элементы матрицы левой части уравнения соответствующим элементам матрицы в правой части. При этом следует учесть что матрица L является симметричной при. То есть в систему уравнений войдут только наддиагональ-ные и диагональные элементы

• Найдём уравнение для элемента 1 1 с учетом того, что уравнение 1 -1 преобразуем к виду Аналогично получим и остальные уравнения.

• Решение системы уравнений достаточно простое. Из (3 3) находим , • подставляем это значение в 2 3, находим • и т. д. . Таким образом найдём все коэффициенты, необходимые для организации закона управления:

12. Применение методов планирования эксперимента для параметрического синтеза САУ ЭМС • Введение • Под параметрическим синтезом будем понимать поиск совокупности варьируемых параметров системы для достижения оптимальных её или заданных свойств. • Поскольку качество системы оценивается на основе критерия качества, то в процессе решения задачи осуществляется либо поиск его экстремума при заданных ограничениях, либо значение критерия, удовлетворяющее заданным условиям. • Для решения таких задач, особенно в условиях действия на систему случайных возмущений и помех, эффективными оказываются методы планирования эксперимента.

• Планирование эксперимента — это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи отыскания оптимальных условий с требуемой точностью. • Если структура регулятора выбрана верно, то критерий качества системы будет функцией параметров регулятора: J=J(Пi). Если такая зависимость найдена, то решение задачи поиска совокупности параметров, доставляющих критерию экстремальное или заданное значение, может быть решена известными методами. Трудность решения за дачи как раз и заключается в том, что функция J(Пi) аналитически может быть найдена лишь в простейших случаях. • В литературе, посвященной методам планирования эксперимента (МПЭ) параметры Пi называют факторами и обозначают как Хi, то есть будем иметь функцию J(Xi).

• Для описания объекта исследования удобно пользо ваться представлением о кибернетической системе, которая схематически изображена на рис. 28. Рис 28 Иногда такую кибернетическую систему называют «черным ящиком» , поскольку при исследовании и решении задачи поиска оптимальных условий ее функционирования необязательно знать ее структуру. Стрелки справа изображают численные характеристики целей исследования (критерии качества), которые в планировании носят название функций отклика.

• То есть в терминологии МПЭ критерий будем иметь в виде Yi=Yi(X). Для проведения эксперимента необходимо иметь возможность воздействовать на поведение «черного ящика» Все способы такого воздействия и являются факторами. То есть мы меняя фактор воздействуем на объект, а на это воздействие объект отвечает изменением значения функции отклика (критерия, меняем параметры меняются свойства системы). • Разложим Yi(X). В ряд Тейлора по степеням X: (12. 1) …. при Х=Х 0 – точка в которой производится разложение функции.

• Вычисление коэффициентов осуществляется по результатам проведенного эксперимента. Очевидно, точное значение производной вычислить нельзя. Приближенное вычисление согласно выражению: • То есть для вычисления необходимо варьировать фактор (параметр) на двух уровнях Х 0+ΔХ и Х 0 ΔХ. . Для вычисления первой производной необходимо поставить эксперимент в двух точках, для вычисления второй не менее, чем в трех точках и т. д. . То есть с ростом порядка растет и время вычисления.

• Ограничимся в (12. 1) только первыми членами ряда, содержащего переменные и их произведения в первой степени. • • (12. 2) Получили функцию отклика в которую все перемен ные входят в первой степени. По своей сути она представ ляет собой модель критерия качества системы в пределах варьирования факторов, то есть в пределах. В то же время вследствие усечения ряда появляется. Вероятность того, что эта ошибка достигнет максимума в ошибточке ка усечения: Х 0 (на рис. 28 эта ошибка обозначена как ε 0), наиболее высокая по сравнению с другими точками. При проведении эксперимента, как правило, известна требуемая точность аппроксимации

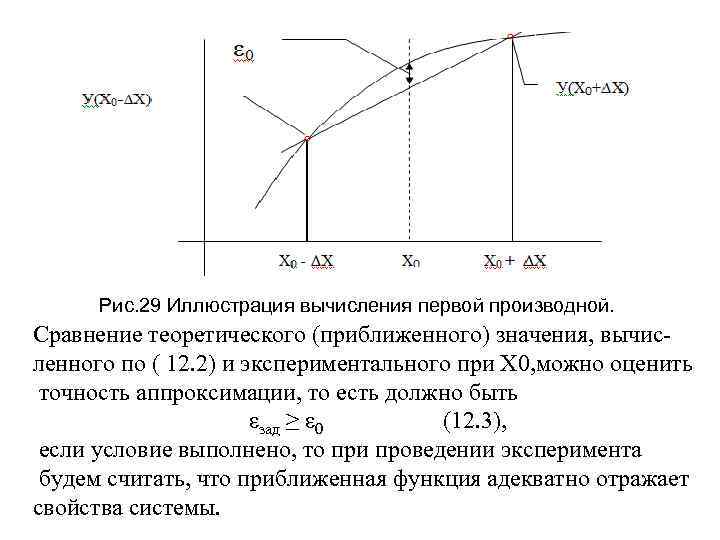Рис. 29 Иллюстрация вычисления первой производной. Сравнение теоретического (приближенного) значения, вычис ленного по ( 12. 2) и экспериментального при Х 0, можно оценить точность аппроксимации, то есть должно быть εзад ≥ ε 0 (12. 3), если условие выполнено, то при проведении эксперимента будем считать, что приближенная функция адекватно отражает свойства системы.

• Для построения линейных моделей, как показано на рис. 29, оказывается достаточно варьирования факторов на двух уровнях. Для одного фактора это прямая линия, для двух факторов это плоскость, для большего числа гиперплоскость. • Цель проведения эксперимента найти такое Х, при котором система будет оптимальной в смысле принятого критерия качества. Независимо от числа факторов при выполнении условия (12. 3) экстремальное значение функции отклика (12. 2) будет находиться в одной из точек, в которых проводился эксперимент, в нашем случае в точке Х 0 – ΔХ минимум, а в точке Х 0 + ΔХ максимум. при поиске максимума (12. 4) при поиске минимума (12. 5) Если |У(Х 0) - (12. 6) |< εзад то функция на интервале [Х 0 ΔХ … Х 0 + ΔХ] имеет экстремума не

• На рис. 30 изображены проекции сечений некоторой сложной двумерной поверхности, экстремум которой необходимо найти, плоскостью параллельной плоскости Х 10 Х 2 Рис. 30 Иллюстрация процесса поиска экстремума

• Предположим необходимо найти минимум функции и тем или иным способом выбрана начальная точка Х 01, В 4 х точках при Х 01 ± ΔХ 1, Х 02 ± ΔХ 2 проведен эксперимент (область в которой варьировались факторы показана красным цветом, эксперимент 2), При этом минимальное значение получено при Х 01 + ΔХ 1, Х 02 + ΔХ 2 и условие (12. 3) выполнилось на рис итерация обозначена цифрой 1). Поместим в полученную точку следующую относительно которой будем варьировать факторы, обозначив её координаты как Х 01, Х 02 ( на рис итерация обозначена желтым цветом, эксперимент 2). Этот процесс будем продолжать до тех пор пока не выполнится условие (12. 5), предположим это эксперимент 3. 1. Уменьшим интервал варьирования факторов в два раза ΔХ 1= ΔХ 1/2 ΔХ 2= ΔХ 2/2. Экстремум может снова оказаться в одной из 4 точек. Процесс будем продолжать до тех пор пока не выполнится условие ΔХ 1 ≤ ɛф, • где ɛф – заданная точность определения положения экстремума. Эксперимент когда варьирование параметров производится принуди-тельно носит название активного. Таким образом, мы рассмотрели один из возможных алгоритмов поиска экстремума многомерной функции по результатам активного эксперимента Далее рассмотрим вопросы рациональной организации экспери-мента для решения рассмотренной задачи.

Постановка эксперимента • • С такими понятиями как факторы, функция отклика, черный ящик, интервал варьирования факторов мы уже ознакомились. При проведении эксперимента к факторам предъявляются следующие требования: Задание фактора на определенном уровне и поддержание его постоянным в течении всего опыта носит название управления величиной факторов. Отсюда проистекает первое требование к факторам – фактор должен быть управляемым. Фактор не должен являться функцией других факторов Факторы должны быть совместимы Факторы должны быть некоррелированными (статистически независимыми). При подготовке к эксперименту выделяют существенные факторы, то есть те , которые оказывают существенное влияние на величину функции отклика.

• Совокупность допустимых значений фактора называют его областью определения. Конечно, было бы заманчиво описать поведение функции отклика сразу во всей области определения фактора, однако это удается сделать крайне редко. При этом если заранее принять линейную модель функции отклика, то интервал варьирования факторов будет определять требуемая точность аппроксимации реальной гиперповерхности гиперплоскостью. Если ошибка аппроксимации больше допустимой, то, уменьшив интервал, улучшим точность (смотри Рис. 29). Если принять это условие за основу, то это означает, что мы при движении в область экстремума принимаем линейную модель критерия (12. 2), а для принятия решения о его расположении воспользуемся описанным выше алгоритмом.

• Еще до проведения эксперимента необходимо спланировать его проведение, то есть выбрать точки, в которых будем проводить опыты, при этом задача должна быть решена за минимально возможное число опытов. В литературе, посвященной этим вопросам показано, что оптимальной стратегией, с точки зрения минимума опытов, будет стратегия одновременного варьирования факторов, так, чтобы эффект оценивался по всей совокупности опытов. Будем проводить опыты при всех возможных сочетаниях уровней. Поскольку таких уровней два, то полное число сочетаний будет N=2 к, где к – количество факторов. • В области определения надо найти локальную подобласть для планирования эксперимента. Процедура выбора этой подобласти включает два этапа: выбор основного уровня факторов Х 0 и выбор интервалов варьирования факторов ∆Х.

• Выбор основного уровня. Наилучшим условиям, определенным из анализа априорной информации, соответствует комбинация (или несколько комбинаций) уровней факторов. Каждая комбинация является многомерной точкой в факторном пространстве. Ее можно рассматривать как исходную точку для построения плана эксперимента. Назовем ее основным (нулевым) уровнем. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня с координатами Х 0 ±∆ Х. Будем называть один из этих (+) уровней верхним, а второй — нижним ( ). Тогда два интересующих нас уровня можно изобразить двумя точками, симметричными относительно первой. Для упрощения записи и обработки результатов эксперимента используем кодированные значения факторов. Кодированный фактор будет принимать значение +1 при Х= Х 0 +∆ Х и 1 при Х= Х 0 ∆ Х.

Полный факторный эксперимент • Полным факторным экспериментом (ПФЭ) называется эксперимент, позволяющий реализовать всевозможные сочетания факторов. План такого эксперимента для трех факторов представлен в таблице 1. Очевидно, эксперимент будет состоять из N = 23 = 8 опытов. Уровни факторов указаны в 2, 3 и 4 столбцах таблицы, в десятом столбце полученное в каждом из опытов значение функции отклика (количество таких столбцов равняется числу критериев, используемых для оценки свойств объекта исследования). Назначение остальных столбцов рассмотрим ниже. В каждом из опытов указано, на каком уровне должен быть установлен тот или иной фактор. Для простоты записи единица опущена, а указаны только знаки. В каждом из опытов указано, на каком уровне должен быть установлен каждый фактор.

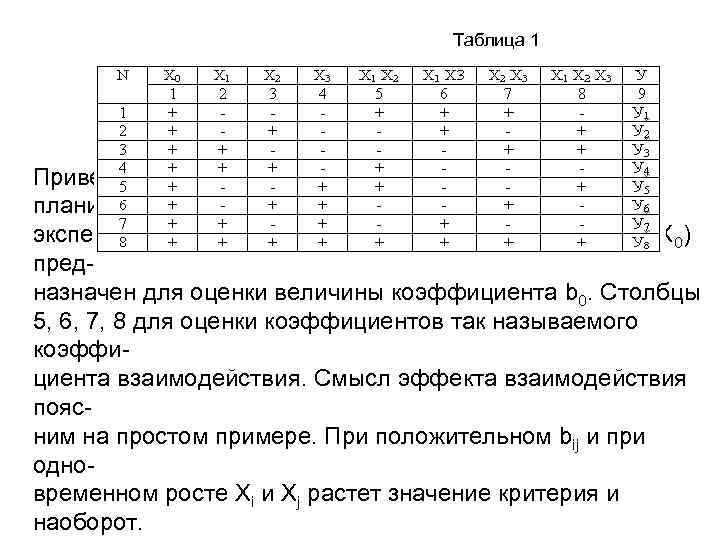Таблица 1 Приведенная таблица носит название матрицы планирования эксперимента. Дополнительные столбцы в матрице 1 - (Х 0) предназначен для оценки величины коэффициента b 0. Столбцы 5, 6, 7, 8 для оценки коэффициентов так называемого коэффициента взаимодействия. Смысл эффекта взаимодействия поясним на простом примере. При положительном bij и при одновременном росте Хi и Хj растет значение критерия и наоборот.

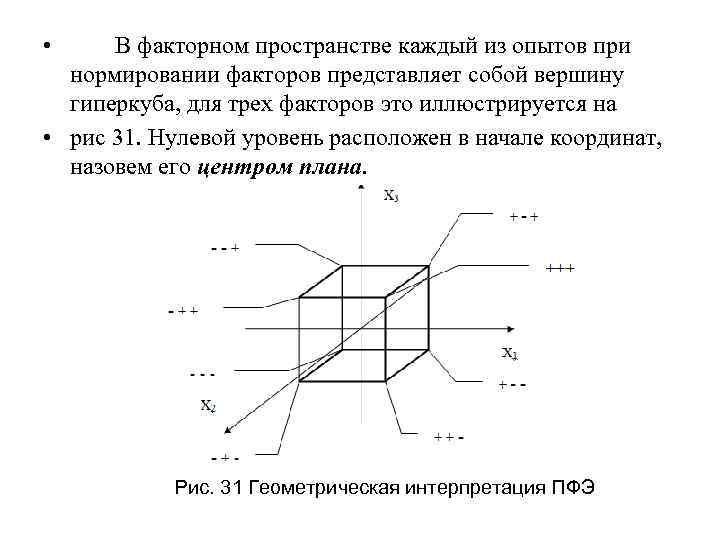• В факторном пространстве каждый из опытов при нормировании факторов представляет собой вершину гиперкуба, для трех факторов это иллюстрируется на • рис 31. Нулевой уровень расположен в начале координат, назовем его центром плана. Рис. 31 Геометрическая интерпретация ПФЭ

Построение плана ПФЭ • Одним из простейших приемов построения плана ПФЭ является следующий: • 1. В столбцах Хi знаки меняются поочередно во втором через один, в третьем через два, в третьем через четыре (при большем числе факторов далее через 8, через 16 и т. д) • 2. Далее меняем местами 2 и 3 столбцы. • 2. Столбцы для оценки коэффициентов взаимодействия получаем путем перемножения соответствующих элементов столбцов Хi.

• Первое из них — симметричность относительно центра эксперимента — алгебраическая сумма элементов вектор столбца каждого фактора равна нулю. • где j – номер фактора • • Второе свойство — условие нормировки — сумма квадратов элементов каждого столбца равна числу опытов. • Третье свойство сумма почленных произведений любых двух вектор столбцов матрицы равна нулю: • . Свойство носит название ортогональности и • позволяет вычислить все коэффициенты уравнения независимо друг от друга. • Последнее, четвертое свойство называется ротабельностью, т. е. точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления

Оценка коэффициентов модели • Для нашего случая имеем следующую линейную модель • Наша цель — найти по результатам эксперимента значения неизвестных коэффициентов модели. Можно утверждать, что эксперимент проводится для проверки гипотезы о том, что линейная модель адекватна. Займемся вычислением оценок коэффициентов. Их можно вычислить по простой формуле Воспользуемся ей для подсчета коэффициентов b 1.

• Вы видите, что благодаря кодированию факторов расчет коэффициентов превратился в простую арифметическую процедуру. Для подсчета коэффициента b 1 используется вектор столбец Х 1, для b 2 — столбец Х 2 и т. д Можно показать, что bо есть среднее арифметическое значение критерия. Поэтому, чтобы его получить, необходимо сложить все Yi и разделить полученную сумму на число опытов, отсюда появляется столбе Х 0, где все элементы принимают значение +1. • Теперь у нас есть все необходимое, чтобы найти неизвестные коэффициенты линейной модели. • Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше численная величина коэффициента, тем большее влияние оказывает фактор. Если коэффициент имеет знак плюс, то с увеличением значения фактора функция отклика увеличивается, а если минус, то уменьшается. Величина коэффициента соответствует вкладу данного фактора в величину критерия при переходе фактора с нулевого уровня на верхний или нижний.

Дробный факторный эксперимент • Число опытов в полном факторном эксперименте превышает число коэффициентов линейной модели, причем тем больше, чем больше факторов. Разность между числом опытов и числом коэффициентов во многих случаях оказывается достаточно велика, и появляется возможность сократить число опытов необходимых для определения коэффициентов. • В качестве примера возьмем 2 х факторный экспе римент, матрица планирования которого имеет вид: •

• Пользуясь таким планированием, можно вычислить четыре коэффициента и представить результаты эксперимента в виде неполного квадратного уравнения: • у = bо + b 1 х1 + b 2 х2 +b 12 x 1 x 2 • Если имеются основания считать, что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить три коэффициента; bо, b 1 и b 2. Остается одна степень свободы. Употребим ее для минимизации числа опытов. При линейном приближении b 12 → 0 и вектор столбец х1 х2 можно использовать для нового фактора х3. Поставим этот фактор в скобках над взаимодействием х1 х2 и посмотрим, каковы будут оценки коэффициентов. Здесь уже не будет тех раздельных оценок, которые мы имели в полном факторном эксперименте 2 к. Оценки смешаются следующим образом: • b 1 → β 1 + β 23; b 2= β 2 + β 13 : b 3= β 3 + β 12

• Но мы принимаем линейную модель, и, следовательно, все парные взаимодействия незначимы. Главное, мы нашли средство минимизировать число опытов: вместо восьми опытов для изучения трех факторов оказывается можно поставить четыре. Найденное правило можно сформулировать так: чтобы сократить число опытов, нужно новому фактору присвоить вектор - столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Тогда значение нового фактора в условиях опытов определяется знаками этого столбца. • Поставив четыре опыта для оценки влияния трех факторов, мы воспользовались половиной полного факторного эксперимента 23, или «полурепликой» . Матрица из восьми опытов для четырехфакторного планирования будет полурепликой от полного факторного эксперимента 24

Полуреплика от ПФЭ 24

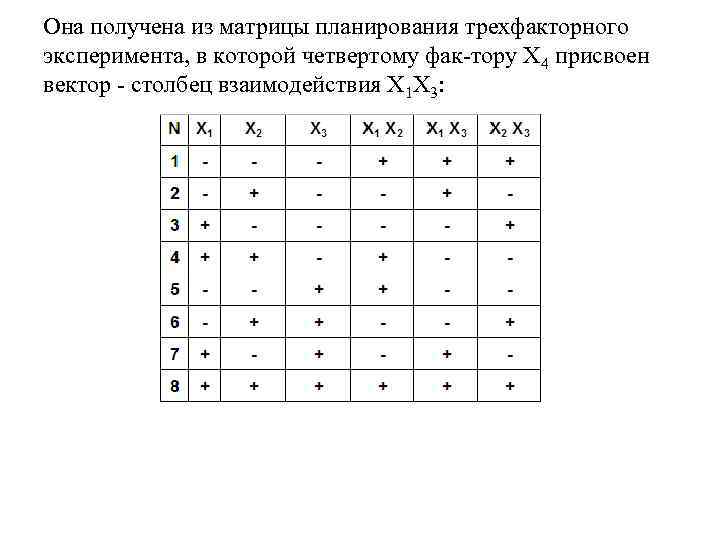Она получена из матрицы планирования трехфакторного эксперимента, в которой четвертому фак тору Х 4 присвоен вектор столбец взаимодействия Х 1 Х 3:

• В каждом эксперименте дополнительно необходимо провести ещё один опыт в центре плана, то есть при Хi = Xi 0 для оценки адекватности полученной модели. Как уже говорилось выше, модель критерия будет адекватной, если теоретическое значение функции отклика равное b 0 будет отличаться от экспериментального на величину не большую ɛ, где ɛ заданная точность аппроксимации. • Планирование эксперимента включает в себя комплекс вопросов, направленных на повышение эффективности экспериментальных исследований. Позволяет значительно интенсифицировать труд исследователя, сократить сроки и затраты на эксперимент, повысить достоверность выводов по результатам исследований. Получить результат при малом объеме априорной информации.