Теория алгоритмов Лекция № 1

Теория алгоритмов Лекция № 1

Структура курса • Лекции – 18 часов • Лабораторные работы – 34 часа (8 л. р. ) • Самостоятельная работа – 64 часа • Экзамен

Графік оцінювання, балів на тиждень Лекції 0, 5 0, 5 0, 5 4, 5 Практичні заняття Методи конролю Лабораторні заняття 0, 5 0, 5 0, 5 0, 5 0, 5 8, 5 Захист лабораторних робіт 4 5 4 4 4 33 Есе Експрес-опитування 0, 5 0, 5 4 Поточні КР 5 10 Екзамен 40 ВСЬОГО балів на тиждень 1 5 1 6 1 5 6 5 1 5 1 6 5 40 100 НАКОПИЧЕННЯ балів 1 6 7 13 14 19 20 25 31 36 37 42 43 48 49 55 60 100 Лекції 4, 5 Лабораторні заняття 8, 5 Захист лабораторних робіт 33 Експрес-опитування 4 Поточні КР 10 Екзамен 40 Всього 100

Литература

Зачем изучать теорию алгоритмов?

Алгоритмы лежат в основе компьютерных наук и разработки программного обеспечения. Реальная производительность любой программной системы зависит только от двух вещей: • выбранного алгоритма • эффективности его реализации. Поэтому разработка хорошего алгоритма критична для производительности всех программных систем. Более того, изучение алгоритмов способствует решению проблем независимо от языка/парадигмы программирования, аппаратного обеспечения и других аспектов реализации Computing Curriculum

Algorithms + Data Structures = Programs Алгоритмы + Структуры данных = Программы Никлаус Вирт — швейцарский учёный, специалист в области информатики, один из известнейших теоретиков в области разработки языков программирования, профессор компьютерных наук.

Если вы считаете себя действительно хорошим программистом. . . , прочитайте "Искусство программирования" (Кнута). . . Если вы сможете прочесть весь этот труд, то вам определенно следует отправить мне резюме. Билл Гейтс.

Что такое алгоритм?

«Алгоритм — это конечный набор правил, который определяет последовательность операций для решения конкретного множества задач и обладает пятью важными чертами: конечность, определённость, ввод, вывод, эффективность» . (Д. Э. Кнут) «Алгоритм — это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи» . (А. Колмогоров) «Алгоритм — это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату» . (А. Марков) «Алгоритм — точное предписание о выполнении в определённом порядке некоторой системы операций, ведущих к решению всех задач данного типа» . (Философский словарь / Под ред. М. М. Розенталя) «Алгоритм — строго детерминированная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд» . (Николай Дмитриевич Угринович, учебник «Информатика и информ. технологии» ) «Алгоритм — это последовательность действий, направленных на получение определённого результата за конечное число шагов» .

Что характеризует любой алгоритм? СЛОЖНОСТЬ

Оценка сложности алгоритмов Виды сложностей: • Временная сложность • Пространственная сложность • Асимптотическая сложность

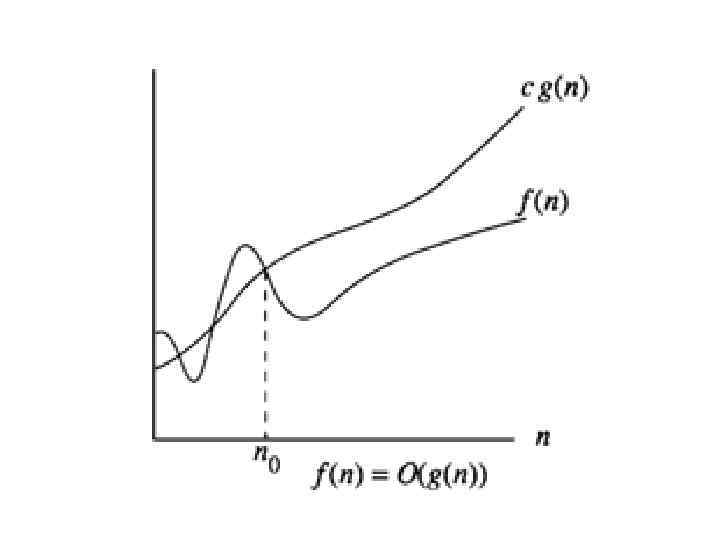
О-нотация Определение. Говорят, что функция f(n) является O(g(n)), если существуют такие постоянные с0 и n 0, что f(n) < c 0 g(n) для всех n > n 0.

Классы оценок сложности - множества вычислительных проблем, для решения которых известны алгоритмы, схожие по сложности n O(1) – постоянное время n O(log(n)) – логарифмическое время n O(n) – линейное время n O(n log(n)) – "n-log-n" время n O(n 2) – квадратичное время n O(n 3) – кубическое время n O(2 n) – экспоненциальное время 15

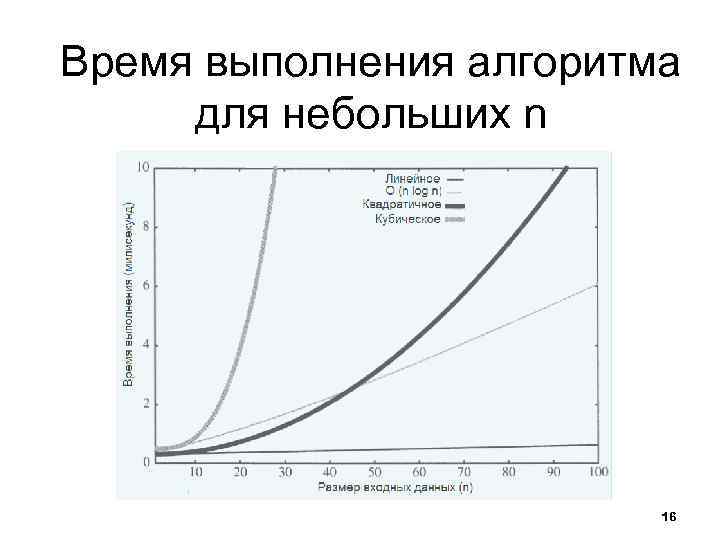
Время выполнения алгоритма для небольших n 16

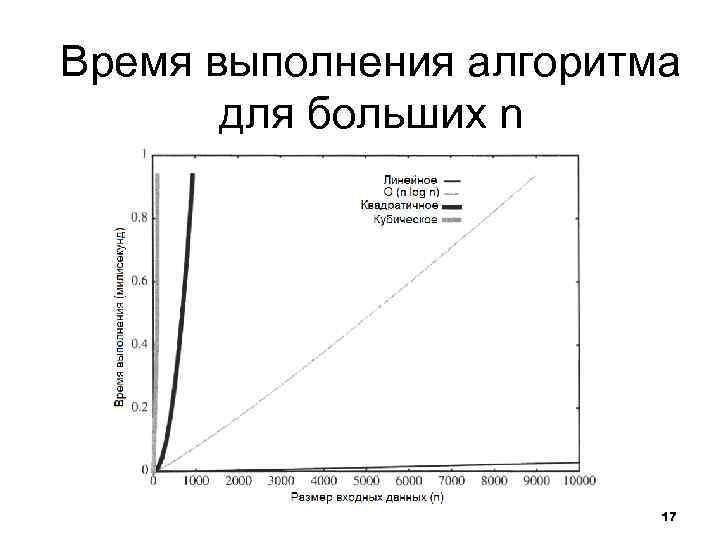
Время выполнения алгоритма для больших n 17

Пример int max=a[0]; t 1 – присваивание for(int i=1; i

Определите сложность следующих алгоритмов: 1. Сложение двух чисел 2. Сложение миллиона чисел 3. Сложение элементов массива из n элементов 4. Сложение элементов двумерного массива, состоящего из n строк и n столбцов 5. Алгоритм возведения числа x в натуральную степень n

Примеры простых алгоритмов для целых чисел • Определить, является ли произвольное целое число простым • Алгоритм Эвклида нахождения НОД • Получить заданное количество первых простых чисел (Решето Эратосфена)

Алгоритм Эвклида нахождения НОД(a, b) = Если a < b, то НОД(a, b) = НОД(b, a mod b) = НОД(b, a), то есть аргументы функции переставляются. Далее при рекуррентных вызовах функции НОД первый аргумент всегда больше второго. Нулем может стать только второй аргумент b.

Решето Эратосфе на

РЕКУРСИЯ

Рекурсия • Рекурсией называется такой способ организации обработки данных, при котором программа (или функция) вызывает сама себя или непосредственно, или из других программ (функций). • Функция называется рекурсивной, если во время ее обработки возникает ее повторный вызов, либо непосредственно, либо косвенно, путем цепочки вызовов других функций

Итерация Итерацией называется такой способ организации обработки данных, при котором некоторые действия многократно повторяются, не приводя при этом к рекурсивным вызовам программ (функций). Теорема. Произвольный алгоритм, реализованный в рекурсивной форме, может быть переписан в итерационной форме и наоборот.

Пример рекурсии Факториал числа. Факториалом целого неотрицательного числа n называется произведение всех натуральных чисел от 1 до n и обозначается n!. Если f(n) = n!, то имеет место рекуррентное соотношение:

Реализация рекурсивная циклическая реализация int f(int n) { { if(n==0) int i, res = 1; return 1; for(i=1; i<=n; i++ return n*f(n-1); ) } res=res * i; return res; }

Рекурсивные задачи • Задача о восьми ферзях • Задача о «Ханойских башнях»

Рекурсивные задачи • Задача о восьми ферзях. Расположить 8 ферзей на шахматной доске так, чтобы они не находились друг у друга " под боем".

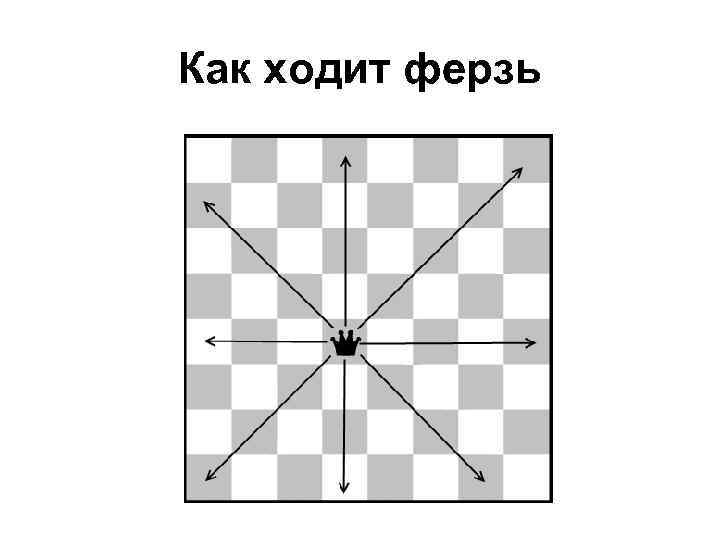
Как ходит ферзь

Способы решения задачи • Полный перебор • «Умный перебор» • Поиск с возвратом

Ставим первого ферзя на поле а 8. После чего просматриваем поля второго столбца сверху вниз - ищем поле, которое не бьётся уже поставленными ферзями. Как только такое поле найдётся - ставим на него ферзя.

Аналогично поступаем с третьим, четвёртым и пятым ферзями

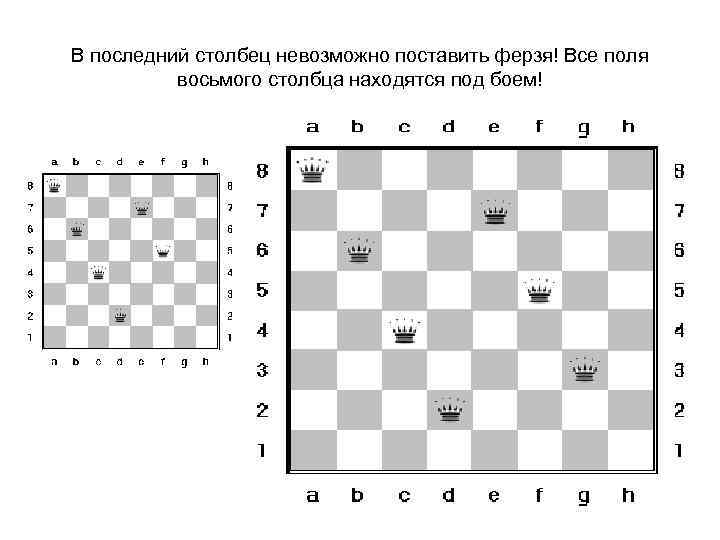
В последний столбец невозможно поставить ферзя! Все поля восьмого столбца находятся под боем!

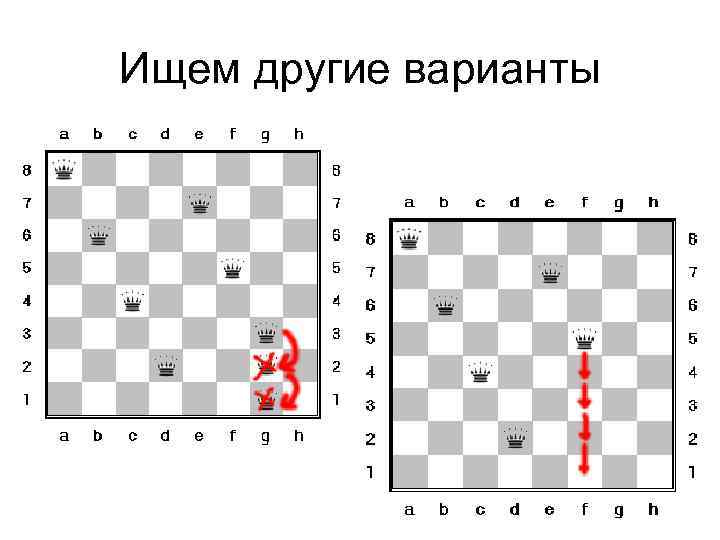
Ищем другие варианты

Одно из решений задачи

Ханойские башни: • В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.

Рекурсивное решение: Пусть необходимо перенести n дисков со стержня (a) на стержень (c). Допустим у нас есть функция перенесения n -1 диска, тогда задача легко разрешима. Для этого вначале перенесем n-1 диск со стержня (a) на стержень (b), применяя рекурсивный вызов той же функции, затем перенесем n-ый диск со стержня (a) на стержень (c) и наконец перенесем n-1 диск со стержня (b) на стержень (c). Работа выполнена.

Функция на C++ void Step(int n, char a, char b, char c) // n - количество колец; // a, b, c - башни; { // т. к. на каждом шаге количество колец будет уменьшаться на один, // это условие будет условием выхода из рекурсии if (n <= 0) return; Step(n-1, a, c, b); cout<<"диск"<

Алгоритмические стратегии • Алгоритмы полного перебора • "Жадные" алгоритмы • Алгоритмы "разделяй и властвуй" • Перебор с возвратом • Метод ветвей и границ • Эвристики

Полный перебор (или метод «грубой силы» от англ. brute force) — метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от количества всех возможных решений задачи. Если пространство решений очень велико, то полный перебор может не дать результатов в течение нескольких лет или даже столетий.

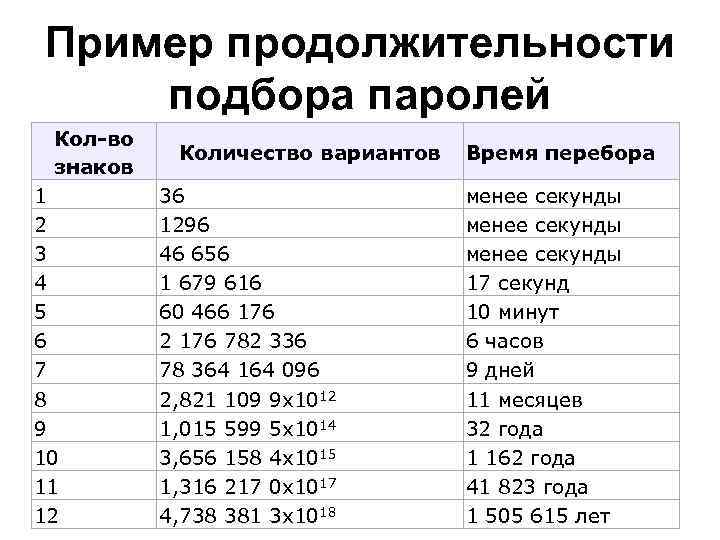
Пример продолжительности подбора паролей Кол-во Количество вариантов Время перебора знаков 1 36 менее секунды 2 1296 менее секунды 3 46 656 менее секунды 4 1 679 616 17 секунд 5 60 466 176 10 минут 6 2 176 782 336 6 часов 7 78 364 164 096 9 дней 8 2, 821 109 9 x 1012 11 месяцев 9 1, 015 599 5 x 1014 32 года 10 3, 656 158 4 x 1015 1 162 года 11 1, 316 217 0 x 1017 41 823 года 12 4, 738 381 3 x 1018 1 505 615 лет