
ТЕОРИЯ АЛГОРИТМОВ лекции 34 ч. лаб. 32 ч. (Java, C++) экзамен 2006 / 07

Литература 1. 2. 3. 4. 5. 6. 7. 8. Вирт Н. Алгоритмы и структуры данных. –М. : Мир, 1989. Гладкий А. В. Теория алгоритмов: Уч. пособие КГУ, 1983. Кнут Дональд Э. «Исскусство программирования» , 1995 Котов В. М. Информатика. Методы алгоритмизации 8 -9 кл. – Мн. : «Народная асвета» , 2000. Липский В. Комбинаторика для программистов. –М. : Мир, 1988. Майника Э. Алгоритмы оптимизации на сетях и графах. М. : Мир, 1981. Новиков Ф. А. Дискретная математика для программистов. Учебник 2001 Писсанецки С. Технология разряженных матриц. –М. : 2 Мир, 1988.

Разделы курса: o o o Математические основы анализа алгоритмов. Сортировка и порядковые статистики. Структуры данных. Базовые операции над ними, их трудоемкость. Основные алгоритмы на графах. Матрицы и действия с ними. Теория кодирования. 3

Лекция 1. Основные понятия теории алгоритмов Алгоритм и его свойства. o Информация. Количество информации. o Сложность алгоритма. o Математические основы анализа алгоритмов. o Эффективность алгоритма. o РАМ - Равнодоступная Адресная Машина. o

1. 1. Алгоритм и его свойства

Рождение понятия «алгоритм» (algorithm) Algorism (устар. ) – выполнение арифметических действий с помощью арабских цифр. Abū ′Abd Allāh Muhammad ibn Mūsa al-Khwārizmi (ок. 783 г. по 850 г. ) – автор учебника по математике «Kitāb al-jabr wa′l-muqābala» ( «Книга о восстановлении и противопоставлении» ). «Dixit Algorizmi… – Алгоризми сказал…» 6

Эквивалентные определения алгоритмов o o o Тезис Тьюринга: «Всякий алгоритм может быть задан посредством Машины Тьюринга» . Тезис Маркова: «Всякий алгоритм представим в виде нормального алгоритма» . Тезис Чёрча: «Всякая вычислимая арифметическая функция является частично-рекурсивной функцией» . 7

Алгоритм и его свойства 1. 2. 3. 4. 5. 6. Определенность (детерминированность). Понятность (доступность). Результативность (сходимость). Дискретность. Массовость. Конструктивность объектов. 8

Определение алгоритма Под алгоритмом понимается единый метод решения определенного класса однотипных задач, обладающий свойством дискретности, массовости, определенности, результативности и оперирующий конструктивными объектами. 9

Оценка качества (эффективности) алгоритма Определяется: o скоростью сходимости, o временем выполнения, o удобством обращения к алгоритму, o простотой, o удобочитаемостью. 10

Способы описания алгоритма: o o o словесное описание; математическая запись; графическая запись в виде блок-схем, графсхем; запись на искусственном алгоритмическом языке (псевдокоде); запись на одном из языков программирования. 11

Задача: найти сумму и произведение чисел от 0 до 100 12

Задача: найти сумму и произведение чисел от 0 до 100 1 способ Сумма=0+1+2+3+…+99+ +100=5050 2 способ 100 операций сложения 13

Задача: найти сумму и произведение чисел от 0 до 100 1 способ 2 способ Сумма=0+1+2+3+…+99+ Сумма = (1+100)+(2+99)+ +100=5050 +(3+98) + (50+51)= =101*50 = 5050 100 операций сложения 1 операция умножения 14

Задача: найти сумму и произведение чисел от 0 до 100 1 способ 2 способ Сумма=0+1+2+3+…+99+ Сумма= (1+100)+(2+99)+ +100=5050 +(3+98) + (50+51)= =101*50 = 5050 100 операций сложения 1 операция умножения Произведение = =0*1*2*…*99*100=0 100 операций умножения 15

Задача: найти сумму и произведение чисел от 0 до 100 1 способ 2 способ Сумма=0+1+2+3+…+99+ Сумма = (1+100)+(2+99)+ +100=5050 +(3+98) + (50+51)= =101*50 = 5050 100 операций сложения 1 операция умножения Произведение = =0*1*2*…*99*100=0 Произведение = =0*любое число = 0 100 операций умножения 0 операций 16

Правильный алгоритм o Алгоритм считается правильным, если на правильным любом допустимом (для данной задачи) входе он заканчивает работу и выдает результат, удовлетворяющий требованиям задачи. В этом случае говорят, что алгоритм решает данную задачу. 17

Этапы разработки программ: 1. 2. 3. 4. 5. 6. 7. 8. Анализ постановки задачи. Построение математической модели. Разработка алгоритма. Анализ алгоритма. Доказательство правильности алгоритма. Реализация алгоритма. Тестирование программы. Оформление документации. 18

Типы ошибок 1. 2. 3. Синтаксические. (а*(b*(c+d))+a. Семантические. S/N, где S-строка, N-число. Логические. Расстояние = скорость + время. 19

1. 2. Информация. Количество информации

Количество информации o o А, В – события некоторого ВП Количество информации, которую получают о событии А, наблюдая событие В, определяется как число 21

Количество информации 2. I(A|B)=I(B|A)≡I(A; B) Пусть события А и В независимы, тогда Р(А|В) = Р(А) 3. Если А=В или Р(А|В) = 1, то 1. 22

Пример 1. o o Имеется 8 бильярдных шаров, пронумерованных от 1 до 8. Какого количества информации достаточно для установления номера выбранного случайным образом шара? Р(А) = 1/8, I (А) = -log 2(1/8)) = 3 23

Пример 2. o o Предположим, что на вход поступает некоторое число X, которое может быть выбрано из интервала [1, …, m], причем любой выбор является равновероятным. Какого количества информации достаточно для определения того, какое конкретно число мы выбрали? Р(А) = 1/m, I (А) = -log 2(1/m)) =log 2(m) 24

1. 3. Сложность алгоритма

Размерность задачи o o o Пример 3. Предположим, что на вход некоторого алгоритма поступают два числа: a, b. Определите размерность задачи, т. е. количество информации, достаточной для задания этих чисел. Пример 4. Предположим, что на вход поступает п чисел {а 1, а 2, …, аn}. Определите размерность задачи. 26

Определения o Временнáя сложность алгоритма o Емкостная сложность алгоритма o асимптотическая временная сложность o асимптотическая емкостная сложность 27

Мера сложности при данной размерности o o сложность в худшем случае, средняя или усредненная сложность. Алгоритм с наименьшей сложностью худшем случае не обязательно имеет лучшую скорость среднем. 28

1. 4. Математические основы анализа алгоритмов

Асимптотические обозначения o o o Θ-обозначение O-обозначение Ω-обозначение 30

1. 5. Эффективность алгоритмов Полиномиальный алгоритм f(l) = O(р(l)) o Экспоненциальный алгоритм f(l) = Ω(exp(l)) o
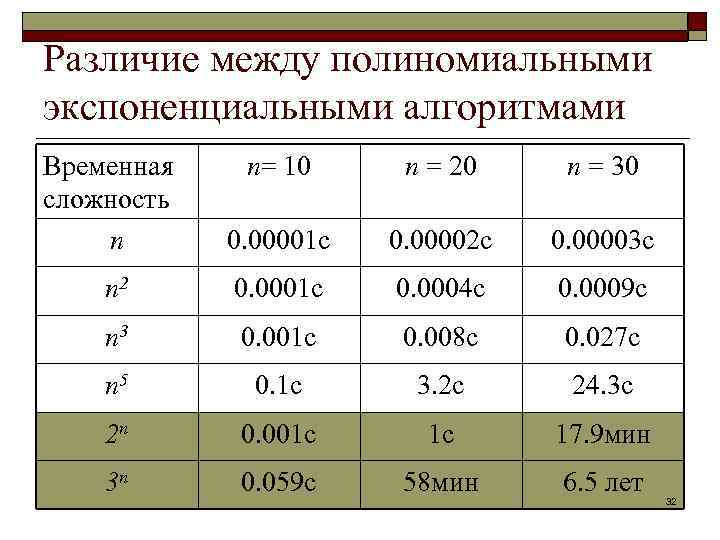
Различие между полиномиальными экспоненциальными алгоритмами Временная сложность п n= 10 n = 20 n = 30 0. 00001 c 0. 00002 c 0. 00003 c п 2 0. 0001 c 0. 0004 c 0. 0009 c п 3 0. 001 c 0. 008 c 0. 027 c п 5 0. 1 c 3. 2 c 24. 3 c 2 п 0. 001 c 1 c 17. 9 мин 3 п 0. 059 c 58 мин 6. 5 лет 32

1. 6. РАМ - Равнодоступная Адресная Машина

Равнодоступная Адресная Машина вычислительная машина с одним сумматором, в которой команды программы не могут изменять сами себя Состоит из o входной ленты, которой она может только считывать, o выходной ленты, на которую она может только записывать, o памяти, которая состоит из последовательности регистров. o 34

Равномерный весовой критерий o o каждая команда затрачивает одну единицу времени, каждый регистр использует одну единицу памяти. 35

Лекция 2. РЕКУРРЕНТНЫЕ УРАВНЕНИЯ Понятие рекуррентного уравнения o Решение рекуррентных уравнений n. Метод итераций; n. Подстановочный метод n. Метод рекурсивных деревьев o Примеры рекуррентных уравнений o