Теоретические основы защиты атмосферы от газовых загрязнений Основные

Теоретические основы защиты атмосферы от газовых загрязнений Основные методы очистки газов Абсорбция газовых примесей

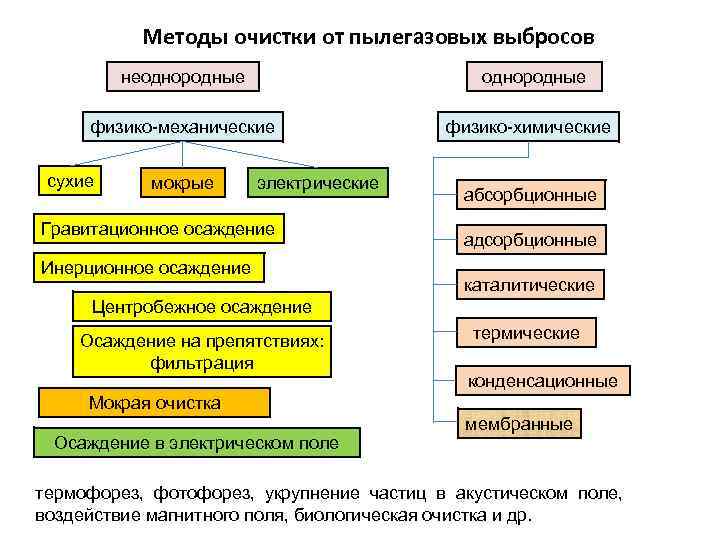Методы очистки от пылегазовых выбросов неоднородные физико-механические сухие мокрые электрические Гравитационное осаждение Инерционное осаждение физико-химические абсорбционные адсорбционные каталитические Центробежное осаждение Осаждение на препятствиях: фильтрация термические конденсационные Мокрая очистка Осаждение в электрическом поле мембранные термофорез, фотофорез, укрупнение частиц в акустическом поле, воздействие магнитного поля, биологическая очистка и др.

Основные методы очистки газов. Методы очистки газовых выбросов чрезвычайно разнообразны и зависят от физ-хим. св-в загрязняющего в-ва, его агр. состояния, концентрации в очищаемой среде и др. Промышленные способы очистки газовых выбросов от газо- и парообразных токсичных загрязнений основаны на двух принципах: . В основном для газоочистки используют методы и средства хим. технологии. Чаще всего применяются жидкостями; тв. поглотителями; , а также методы (сжигание или дожигание горючих загрязнений). В меньших масштабах используют конденсацию, хим. взаим-е примесей с сухими поглотителями и окисление озоном. В соответствии с классификацией процессов и аппаратов химической промышленности для реализации этих задач используют соответствующие аппараты. К ним относятся: абсорберы, адсорберы, конденсаторы, установки (печи) для термодеструкции (пиролиз, крекинг, риформинг) и для термоокисления (дожигания), термокат. установки (печи, реакторы), хим. реакторы.

Абсорбция газовых примесей Абсорбция – это процесс поглощения (растворения) газа в объёме жидкой фазы. Обр. процесс – выделение растворённого газа из р-ра – это десорбция (дегазация). В абсорбц. процессах участвуют две фазы – жидкая и газовая. Жидкое в-во, в к-ром происходит растворение абсорбируемых компонентов, – растворитель, поглотитель или абсорбент. В-во, входящее в состав газ. фазы и при абсорбции не переходящее в жидкую фазу, называют газом-носителем. В-во из состава газ. фазы, к -рое при абсорбции переходит в жидкую фазу, т. е. поглощаемый компонент, называют абсорбтивом. Это же в-во, поглощённое в объёме поглотителя – абсорбатом. Иногда растворяющийся газ вступает в хим. реакцию с р-лем. Процесс, сопровождающийся хим. реакцией между поглощаемым компонентом и абсорбентом, называют химической абсорбцией (хемосорбция). Соот-но, процесс, завершающийся физ. растворением абсорбата в поглотителе, называют физ. абсорбцией (– абсорбция). Инертный газ и жидкость-поглотитель являются носителями извлекаемого компонента, соответственно, в газовой и жидкой фазах.

. Абсорбция представляет процесс хим. технологии, включающий массоперенос г/о компонента между газовой и жидкой фазами, осуществляемый в массообменных аппаратах – абсорберах. Абсорбция газов жидкостями – наиболее распространенный процесс очистки газ. выбросов. Абс. методы используют для технол. и сан. (экологической) очистки газов. Она применяется в пром-сти для извлечения из газов или воздуха диоксида серы, H 2 S и др. сернистых соединений, оксидов азота, паров кислот (НСl, HF, H 2 SO 4), диоксида и оксида углерода, разнообразных летучих орг. соединений (фенол, формальдегид, летучие растворители и др. ). Применение абсорбции особенно эффективно при значительных конц-циях г/о загрязнителей. Считается целесообразным применять абсорбцию, если конц-ция данного компонента в газовом потоке составляет свыше 1 %. Однако возможно её применение при весьма низких конц-циях, когда раст-мость газа в жидкости очень высока. В качестве абсорбента можно использовать любую жидкость, включая расплавы, которая растворяет извлекаемый компонент.

Теор. основами процессов очистки газ. выбросов от загряз-х в-в служат Идеальными считают смеси газов и жидкие р-ры, обр-ние к-рых не сопровождается тепловыми и объёмными эффектами, связанными с хим. или межмол-ным взаим-виями между компонентами. Для смеси ид. газов и ид. р-ра хим. потенциал μi каждого компонента i имеет простую логарифм. зав-сть от его конц-ции (ех, от мольной доли xi): μi = μ 0 i(p, T) + RT lnxi, где μ 0 i – хим. потенциал чистого компонента, зависящий только от давления р и т-ры Т, R — универ. газ. пост. В реальных р-рах такие взаим-я присутствуют обязательно, что приводит к разл. отклонениям от идеальности. Это делает невозм-м точный учёт влияния разл. факторов на св-ва реальных р-ров. Наиболее близкими к идеальным явл-ся очень разб. р-ры, к-рые подчиняются законам Генри, Рауля и Дальтона. По своей природе и св-вам р-ры газов в жидкости ничем не отличаются от др. жидких р-ров. Обычно р-ры при газоочистке имеют невысокую конц-цию газов, что позволяет с достаточной для практики точностью применять для них законы идеальных растворов.

В соот-вии с з-ном Дальтона общее давление П газовой смеси равно сумме парц. давлений р всех её компонентов П = р1 + р2 + …+ рi. (1) Мольная (объёмная) доля у любого компонента смеси ид. газов на основании ур-ний Клапейрона и Дальтона равна: уi = рi /П, (2) где рi – парц. давление i -го компонента газ. смеси, Па; П – общ. давление смеси газов, Па. Растворение газов в жидкостях процесс обратимый, поэтому в двухфазной системе газ – раствор при пост. условиях с течением времени устанавливается равновесие: абсорбция – десорбция. Пар, находящийся в т/д равновесии с жидкостью, наз-ся насыщенным. Равновесные конц-ции компонентов в соприкасающихся фазах опрся з-ном распределения в-ва (В. Нернст), к-рый устанавливает постоянное соотношение между равновесными конц-циями в-ва в обеих фазах при опр. т-ре. Это постоянство не нарушается при изменении нач. конц-ции компонента или общ. давления в системе.

Законы Генри и Рауля рассматриваются как его частные случаи для равновесий в системе жидкость – газ. Конц-ция насыщ. р-ра явлся мерой растворимости газов, к-рая помимо природы газа и р-ля, в большой степени зависит от т-ры и давления. Влияние давления при его невысоких значениях на процесс растворения газов в жидкостях достаточно хорошо выражает закон Генри: при постоянной т-ре растворимость газа в растворителе прямо пропорциональна парциальному давлению этого газа над раствором. xi = pi /Ei , (3) где xi – мольная доля i -го компонента в жидкости; pi – парциальное давление i-го компонента в газе при равновесии, Па; Ei – коэффициент Генри, Па. С ростом темп-ры растворимость газов в жидкостях уменьшается. Объединяя ур-ния 2 и 3 подстановкой значения р* = у*П, получаем у* = (Е/П) х, (4) где р* – равновесное парциальное давление компонента в газовой фазе над равновесной с газом жидкостью, у* – мольная доля компонента в газ. фазе, равновесной с р-ром.

Сведения о равновесных составах жидких и паровых фаз различных р-ров при разных т-рах получают опытным путём. Данные о них приводятся в различных справочниках. у* С y* = f(х) О х Рис. 1. Линия равновесия в системе газ – жидкость. Графическое изображение распределения компонентов между фазами при равновесии обычно даётся в виде диаграммы y* = f(х), где по оси абсцисс откладывается концентрация х распределяемого в-ва в жидкой фазе L, а по оси ординат – его равновесная конц-ция у* в газовой фазе G. Кривая ОС, изображающая зав-сть равновесной конц-ции у* от х, наз-ся (рис. 1). Закон Генри представляет собой также и следствие из общего принципа Ле-Шателье. Как правило, растворение газов в воде происходит с выделением тепла и с ум-нием объёма, поэтому в соот-вии с принц. Ле Шателье при повышении т-ры и понижении давления их р-мость снижается.

Движущая сила процесса абсорбции Равновесие в хим. ТД считается самым устойчивым состоянием системы. Стремление к равновесию является движущей силой обратимых хим. р-ций и процессов массопередачи. Непосредственной т. д. хар-стикой хим. и фазовых превращений в системе явл-ся , тогда отклонение от равновесия можно отразить разностью хим. потенциалов в-в, опр-щих начальное и конечное состояние системы. При достижении равновесия их потенциалы выравниваются. Направление самопроизвольного протекания процесса (ех, переход компонента при массопереносе) опр -ся стремлением к убыванию его хим. потенциала. На практике для проведения расчётов используют не хим. потенциалы, а – концентрации. При этом движущие силы массопередачи из газа в жидкость можно представить как отклонение системы от состояния равновесия в виде соответствующей разности его конц-ций в газ. Δу или жидк. Δх фазах: Δу = у* – у и Δх = х – х* (18) у конц-ция щаях переходящего и где компонента, в соот-но, жидк. и газ. фазе; х* и у* – его равновесная конц-ция.

Т. о. , движущая сила процесса абсорбции м. б. отнесена к любой из двух фаз системы. Чем дальше система находится от состояния равновесия, тем больше движущая сила процесса и тем выше скорость абсорбции. Осн. записывается в общ. виде: M = K F Δ (19) где М – кол-во компонента, переходящего из одной фазы в другую; F – площадь поверхности массопередачи; К – коэффициент массопередачи - выражает кол-во вещества, переходящего из одной фазы в другую за единицу времени через единицу поверхности соприкосновения при движущей силе, равной единице. Его размерность зависит от размерности движущей силы; Δ – движущая сила процесса. В процессе абсорбции концентрация извлекаемого компонента в газовой и жидкой фазах меняется по высоте абсорбера. Это означает, что изменяется и движущая сила массопередачи. Поэтому при расчётах пользуются средней движущей силой.

Поскольку движущая сила может быть представлена по газовой и жидкой фазам, то осн. ур-ние массопередачи даётся в двух видах: или (20) где М – расход компонента, переходящего из одной фазы в другую, кмоль/с; F – площадь поверхности массопередачи, м 2; Ку и Кх – коэф-ты массопередачи по газ. и жид. фазе, отнесённые к движ. силе Δу и Δх, выраж. через мол. доли компонента в газовой фазе, кмоль/(м 2·с); Δуср и Δхср – средние движущие силы по газовой и жидкой среде. Ур-ния массопередачи получены на основе аналогии между процессами переноса количества движения, теплоты и массы путём обобщения экспериментальных данных методами теории подобия. В хим. технологии они служат основой расчёта реакционных аппаратов. Для этого необходимо в первую очередь знать численное значение коэффициента массопередачи – наиболее характерного показателя эффективности работы реактора.

Массоперенос в процессе абсорбции В процессе массопереноса при абсорбции различают (перенос в-ва от границы раздела фаз внутрь фазы) и (перенос в-ва из одной фазы в другую через поверхность раздела фаз). При абсорбции перенос вещества из фазы в фазу, также как и в объёме (ядре) обеих фаз обеспечивается диффузией. Диффузия (от лат. diffusio – распространение, растекание, рассеивание) – движение частиц среды, приводящее к переносу в-ва и выравниванию конц-ций или к установлению равновесного распределения конц-ций частиц данного сорта в среде. Диффузия в-ва в процессе массопереноса может осуществляться по разным механизмам, в общем случае различают молекулярную, конвективную и турбулентную диффузию. В отсутствие макроскопического движения среды диффузия молекул (атомов) определяется их тепловым движением (молекулярная диффузия).

– это самопроизвольный перенос вещества в результате хаотического теплового движения молекул. Главной хар-кой мол. диффузии служит плотность диффузионного потока J – кол-во в-ва, переносимого в единицу времени через единицу площади пов-сти, перпендикулярной направлению переноса. Разность конц-ций в жидкости или газе вызывает направленную мол. диффузию. Закономерности молекулярной диффузии описываются законами Фика. определяет величину переноса в-ва при диффузии в направлении n (одномерный случай) в момент времени t: (21) где М – масса переместившегося вещества, кг; F – площадь массопереноса, м 2, t – время, с; – градиент концентрации в направлении переноса; D – коэф-нт молек. диффузии, м/с; знак "минус" указывает на направление потока от больших концентраций к меньшим.

Коэф-нт мол. диффузии D не зависит от времени и глубины проникновения диффундирующего компонента, но зависит от его свойств и свойств среды, в которой происходит диффузия, а также от температуры и давления процесса. Наиболее быстро диффузия происходит в газах, медленнее в жидкостях, ещё медленнее в твёрдых телах, что обусловлено характером теплового движения частиц в этих средах. Коэф-нты диффузии в жидкостях значительно меньше (на 4 – 5 порядков), чем в газах.

В условиях подвижной среды в рез-те перемешивания или движения в потоке перенос в-ва может осуществляться за счёт турбулентной и конвективной диффузии. Перенос массы в ядре потока каждой фазы, где обычно происходит интенсивное перемешивание, осуществляется преимущественно в рез-те турбулентных пульсаций. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ – перенос в-ва в пространстве, обусловленный турбулентным (вихревым) движением среды, при кром элементы (ч-цы) среды совершают неупорядоченные, хаотич. движения по сложным траекториям, а скорость, т-ра, давление и плотность среды испытывают хаотич. флуктуации. Если в турбулентном потоке в опр. момент времени множество элементов (ч-ц) расположено рядом один с другим, то в послед. моменты времени они рассеиваются по пространству так, что статистич. расстояние между любыми двумя произвольными ч-цами с течением времени возрастает. Проявления этого процесса во многом напоминают мол. диффузию. КОНВЕКТИВНАЯ ДИФФУЗИЯ – совокупность двух процессов: направленной молекулярной диффузии, возникающей при наличии разности конц-ций в жидкости или газе, и переноса ч-ц растворённого в-ва самой движущейся жидкостью.

Скорость диффузии определяет скорость процесса абсорбции. Если в неподвижной среде скорость межфазного переноса массы зависит от скорости молек. диффузии, то в движущейся среде – от скорости конвективной диффузии, а также от специфич. условий на границе раздела фаз. При конвект. диффузии перенос в-ва осуществляется со скоростью во много раз превышающей скорость молек. диффузии. Конвект. перенос в-ва под действием турб-ных пульсаций иногда называют турбулентной диффузией. Вследствие чрезвычайной сложности турбулентных двухфазных потоков определение в них пов-сти контакта фаз, распределения конц -ций в фазах и др. параметров, необходимых для расчётов практически невозможно. Предложены разл. модели механизма массопереноса, но область их применения ограничена частными случаями. При описании процесса абсорбции одной из первых считается двухплёночная модель Льюиса и Уитмена и её дальн. развитие в виде модели пограничного дифф. слоя, согласно к-рым изменение конц-ций переходящего в-ва происходит в тонких приповерхностных слоях (плёнках) газа 3 и конденс. в-ва 4 (рис. 2. ).

Перенос массы в ядре потока каждой фазы из-за интенсивного перемешивания осуществляется преимущественно в рез-те турбулентных пульсаций (конвективная диффузия). Поэтому конц-ции переходящего компонента уf в объёме газовой фазы 1 и хf в объёме жидкой фазы 2 ≈постоянны, тогда как в вязких приграничных слоях перенос массы происходит медленнее в рез-те молек. и затухающей конвективной диффузии. Пусть конц-ция yf распределяемого в-ва М в фазе G > равновесной, и в-во переходит из фазы G в фазу L (рис. 2). х, у 1 3 4 2 yf угр G L хгр M xf Рис. 2. Схема процесса массообмена между жидкостью и газом: 1 - ядро газовой фазы G, 2 - ядро жидкой фазы L, 3 - пограничный слой, 4 – пов-сть раздела фаз.

Ур-ние конвективной диффузии: (22) где М – кол-во в-ва, переносимого из фазы, отдающей в-во, к пов-сти раздела фаз (или от пов-сти раздела фаз в фазу, воспринимающую это вещество), кг/с; β – коэффициент массоотдачи, м/с; F – поверхность раздела фаз, м 2; ΔСф-сл – разность конц-ций распред-го в-ва в фазе и у пов-сти раздела, кг/м 3. Ур-ние (22) поясняет физ. смысл коэф-та массоотдачи β и математически выражает экспериментально установленный факт, называемый иногда законом А. Н. Щукарёва – кол-во в-ва, перенесённое в единицу времени через единицу площади пов-сти, пропорционально разности конц-ций у пов-сти раздела фаз и в ядре потока. Коэф-ты массоотдачи βx (в фазе L) и βy (в фазе G) показывают какая масса в-ва переходит от пов-сти раздела фаз в ядро фазы (или в обр. направлении) через единицу площади пов-сти в единицу времени при движущей силе массоотдачи, равной единице. Коэффициент массоотдачи β зависит от гидродинамических, физ. и геометр. факторов и опр-ся экспериментальным путём с обработкой данных при помощи теории подобия.

: При опр. допущениях (отсутствие дифф-го сопротивления при переходе в-ва через пов-сть раздела фаз, существование равновесия на этой пов-сти, линейность ур-ния равновесия y* = f(х)= mх) между коэф-тами массопередачи Ку и Кх и фаз. коэф-тами массоотдачи βу и βх получаются зав-сти : (23) где m – тангенс угла наклона линии равновесия. Соотношение (23) называют иногда ур-нием аддитивности фазовых сопротивлений. Знаменатели представляют общее диффузионное сопротивление, равное сумме диффузионных сопротивлений газовой и жидкой фаз.

Когда осн. диффузное сопротивление сосредоточено в газовой фазе (для хорошо растворимых газов), т. е. при (24) Когда осн. диффузное сопротивление сосредоточено в жидкой фазе (для плохо растворимых газов), т. е. при (25) Из уравнений (24) и (25) следует, что Ку = Кх /m. (26) Коэф-нты массоотдачи зависят от условий соприкосновения газа и жидкости, от размеров аппарата и его конструкции, от гидродинамики потоков, а также от природы в-в. Вследствие недостаточной изученности мех-зма и кинетики массопереноса, особенно в многокомпонентных смесях, расчёт массообменных процессов и аппаратов проводится опытным путём для каждого типа аппаратов. Эти факторы обычно учитывают при помощи критериев подобия.

Приложение теории подобия к процессам массопередачи показало, что эти процессы определяются критерием Рейнольдса Re и диффузионными критериями Нуссельта Nu´ и Прандтля Рr´, являющимися аналогами тепловых критериев Nu и Рг. Критерии Re и Рr´ являются определяющими, критерий Nu´ – определяемым. Зав-сть между критериями выражается в общем виде ур-нием Nu´ = f(Re, Рr'). (26) По найденному значению Nu´ вычисляют коэффициент массоотдачи β. Ниже даны значения диф. критериев и критерия Рейнольдса: Nu' = β·l/D; (27) β = Nu‘D/l Pr'= µ/(ρ·D); 28) Re =w·lρ/µ. (29) где β – коэф-нт массоотдачи, м/с; l – определяющий геометр. размер, м; D – коэф-нт диффузии, м 2/с; µ – динам. вязкость, Па·с; ρ – плотность, кг/м 3; w – скорость, м/с. Конкретный вид зав-сти (26) устанавливается опытным путём.

Материальный баланс абсорбции Схема массообменного аппарата (рис. 3). Пусть компонент переходит из фазы G в фазу L. С учетом количества компонентов в фазах уравнение материального баланса запишется в виде: Gв, Yв Lв, Хв (30) X где Gн, Gв – расход газовой фазы на входе в абсорбер и выходе из него, кмоль/с (кг/с); О Хв, Хн – концентрация распределяемого компонента в жидкой фазе на входе в абсорбер и выходе из него, отн. мольные доли (отн. масс. доли); Y О G н , Yн L н , Хн Рис. 3. Схема движения абсорбата и абсорбента в абсорбере. Lв, Lн – расход абсорбента на входе в абсорбер и выходе из него, кмоль/с (кг/с); Yн, Yв – концентрация распределяемого вещества (компонента) в газовой фазе на входе в абсорбер и выходе из него, отн. мольные доли (отн. масс. доли).

Пусть G и L – const. Тогда, количество компонента М, перешедшего из фазы G, равно: M = G(Yн – Yв ). (31) Количество компонента М, перешедшего в фазу L, равно: M = L(Xв –Xн). (32) Приравняем правые части уравнений (31) и (32): М = G(Yн – Yв) = L(Xв – Xн) (33) где G – расход инертного газа, кмоль/с (кг/с); L – расход абсорбента, кмоль/с (кг/с); Yн и Yв – относительные концентрации компонента в газе-носителе, кмоль/кмоль газа (кг/кг газа); Xв и Xн – относительные концентрации компонента в поглотителе (абсорбенте), кмоль/кмоль абсорбента (кг/кг абсорбента). Уравнение (33) – уравнение материального баланса.

(34) Общий расход абсорбента L равен: Удельный расход поглотителя l, кг/кг: l = L / G. (35) Из уравнений (34) и (35): l = (Yн – Yв)/(Xв – Xн). (36) Рассмотрим произвольное сечение аппарата 0 – 0, где составы фаз будут Y и Х соответственно в фазе G и L (рис. 3). Ур-ние материального баланса для части аппарата, расположенной выше сечения 0 – 0: GY + LXн = GYв + LX. 7) Откуда получим Y= Yв + (X – Xн)L/G или Y = Yв + l (X – Xн). (38) Ур-ние (38) есть уравнение рабочей линии. Оно выражает зав-сть между неравновесными составами фаз в любом сечении аппарата. Из (38) видно, что это уравнение прямой линии (Y = a + b. X). Подставим в уравнение (38) уравнение (36): Y = Yв + (Yн – Yв) (X – Xн)/(Xв – Xн) или (Y – Yв)/(Yн – Yв) = (X – Xн)/( Xв – Xн) (39) (40) Это есть уравнения прямой, проходящей через точку A (Xв; Yв) и точку B (Xн; Yн). Рабочую линию процесса абсорбции строят в тех же осях Y-X, что и линию равновесия: Y = Yв + l (X – Xв) = Yв + (Yн – Yв) (X – Xн)/(Xв – Xн). (41)

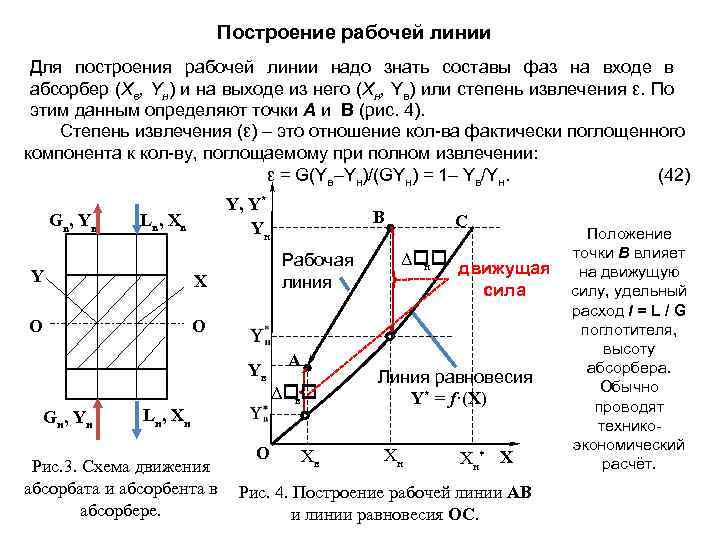Построение рабочей линии Для построения рабочей линии надо знать составы фаз на входе в абсорбер (Хв, Yн) и на выходе из него (Хн, Yв) или степень извлечения ε. По этим данным определяют точки А и B (рис. 4). Степень извлечения (ε) – это отношение кол-ва фактически поглощенного компонента к кол-ву, поглощаемому при полном извлечении: ε = G(Yв–Yн)/(GYн) = 1– Yв/Yн. (42) Gв, Yв Y, Y* Yн Lв, Хв Y Рабочая линия X О В О Yв G н , Yн L н , Хн Рис. 3. Схема движения абсорбата и абсорбента в абсорбере. О А Δ в Хв С Положение точки В влияет Δ н движущая на движущую сила силу, удельный расход l = L / G поглотителя, высоту абсорбера. Линия равновесия Обычно Y* = f·(Х) проводят техникоэкономический * Х Хн Хн расчёт. Рис. 4. Построение рабочей линии АВ и линии равновесия ОС.

На рис. 4 видно, что по мере прохождения потоков по абсорберу движущая сила меняется. ех. ΔYн и ΔYв. Поэтому при расчётах пользуются средней движущей силой, величину которой рассчитывают по-разному. 1) Если линия равновесия прямая, то исп-ся средняя логарифмическая движущая сила: (43) 2) Когда отношение 0, 5 ≤ ΔYн /ΔYв ≤ 2, то среднюю движущую силу рассчитывают как среднюю арифметическую: ΔYср = (ΔYн /ΔYв)/ 2. (44) 3) Если линия равновесия не прямая, то применяется средняя интегральная движущая сила: (45) Величину интеграла определяют графическим построением или интегрированием. Др. метод основан на делении равновесной линии на неск. отрезков и для каждого из них определяют ср. дв. силу как среднеарифметическую или среднелогарифмическую. После того, как определены основные составляющие уравнения массопередачи рассчитываются параметры абсорбера (поверхность раздела фаз, диаметр, высота).

Расчёт параметров абсорбера. Определение диаметра абсорбционной колонны D (в м) проводят по уравнению расхода газового потока: (46) где V – расход газа, проходящего через абсорбер, м 3/с; w – скорость газа, отнесённая к полному поперечному сечению колонны (фиктивная), м/с. Определение высоты абсорбционной колонны Н (в м) может проводиться двумя путями: а) через высоту единицы переноса (ВЕП) б) через высоту, эквивалентную теоретической тарелке (ВЭТТ). Наличие двух методов расчёта кинетики массообмена связано с применением разных аппаратов а) в колоннах с непрерывным контактом фаз - насадочным, пленочным и др. б) в колоннах с дискретным контактом фаз - тарельчатые аппараты.

а) через ВЕП сначала определяют поверхность F контакта фаз в абсорбере при плёночном режиме работы: F = Hн S·σ·φ, (47) где Нн – высота слоя насадки, м; S = πD 2/4 – площадь поперечного сечения цилиндрической колонны, м 2; D – диаметр колонны, м; σ – удельная поверхность сухой насадки, м 2/м 3; φ – коэффициент смоченности насадки, безразмерный. Высота слоя насадки: (48) где G – const по высоте колонны расход инертного газа, кг/с или кмоль/с; Ky – средний коэффициент массопередачи, кг/(м 2·с·/кг инерт. газа) или кмоль/(м 2·с·/кг инерт. газа); h 0 у – высота единицы переноса, м: n 0 y – общее число единиц переноса: Из уравнения (45) следует, что:

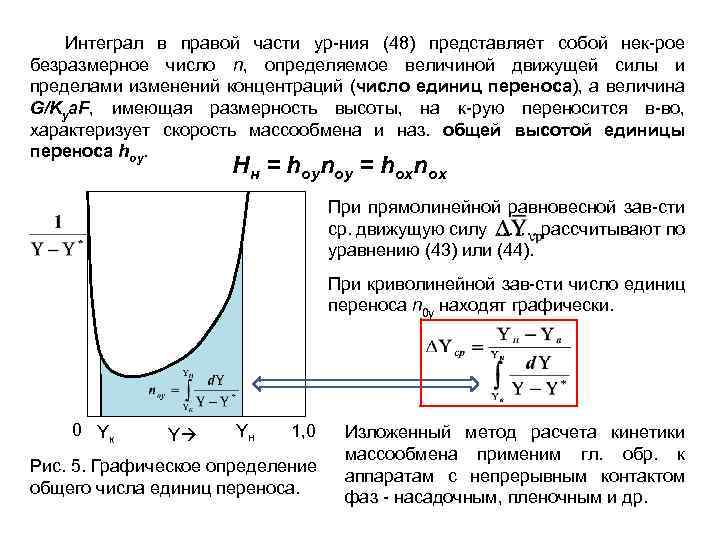Интеграл в правой части ур-ния (48) представляет собой нек-рое безразмерное число n, определяемое величиной движущей силы и пределами изменений концентраций (число единиц переноса), а величина G/Kya. F, имеющая размерность высоты, на к-рую переносится в-во, характеризует скорость массообмена и наз. общей высотой единицы переноса hoy. Hн = hoynoy = hoxnox При прямолинейной равновесной зав-сти ср. движущую силу ……. рассчитывают по уравнению (43) или (44). При криволинейной зав-сти число единиц переноса n 0 y находят графически. 0 Yк Y Yн 1, 0 Рис. 5. Графическое определение общего числа единиц переноса. Изложенный метод расчета кинетики массообмена применим гл. обр. к аппаратам с непрерывным контактом фаз - насадочным, пленочным и др.

б) Через высоту, эквивалентную теоретической тарелке (ВЭТТ). Эффективность массообменного аппарата м. б. выражена также через число теоретич. ступеней контакта или число теоретич. тарелок, а кинетич. характеристика – через кпд, что часто используется для описания массообмена в колоннах с дискретным контактом фаз (Тарельчатые аппараты), или через высоту, эквивалентную теоретической ступени контакта (ВЭТТ). Число теоретич. тарелок м. б. найдено аналитически путем совместного решения ур-ний, описывающих равновесную и рабочую линии процесса, или графически. В последнем случае строятся ступени между рабочей и равновесной линиями в пределах заданных концентраций. Одна теоретич. тарелка выражает одно изменение движущей силы по газовой Δу. А и по жидкой Δx. А фазам (чем больше движущая сила, тем меньше потребуется теоретич. тарелок для заданного разделения).

Теоретическая ступень изменения концентрации (теоретическая тарелка). Пусть процесс идёт из фазы х в фазу у (т. е. у < у*). Примем такой объём аппарата конц-ция распределяемого в-ва на выходе из к-рого у2 равна равновесной конц-ции на входе в него, т. е. у2 = у1* - точка В на рис. 6. Соотв-но изм-ние состава в фазе у в этом же объёме изобразится на рис. 6 отрезком АВ. xн ук у у2* у* = mx x 2 у1*= у2 x 1 у1 xк ун y 1 C В А x 1 y=ax+b x 2 x Рис. 6. Схема изменения концентраций в противоточном аппарате (а) и её отражение на диаграмме у – х (б). В этом объёме аппарата происходит процесс полного (теоретического) обмена распределяемого вещества между обеими фазами. Такое изменение концентрации называют теоретической ступенью изменения концентрации или теоретической тарелкой. Строя такие ступени между рабочей линией и линией равновесия в заданном интервале рабочих концентраций, находят общее число ступеней nт (число теоретических тарелок – ЧТТ, или число теоретических ступеней – ЧТС) для данного процесса.

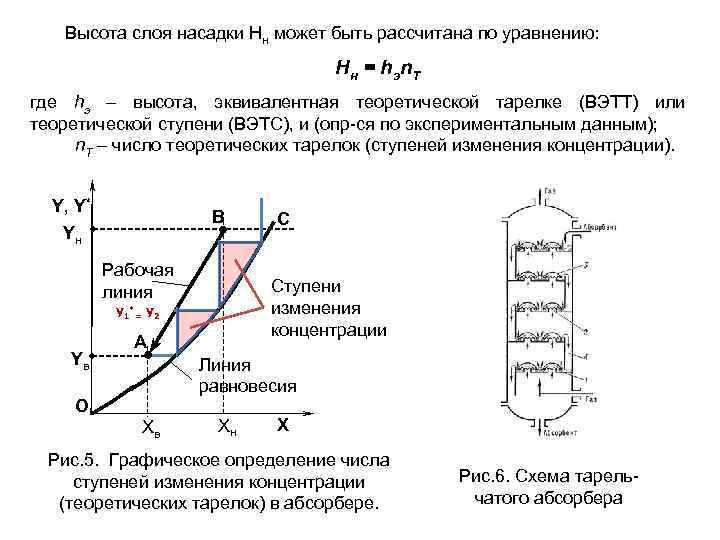Высота слоя насадки Нн может быть рассчитана по уравнению: Нн = hэn. Т где hэ – высота, эквивалентная теоретической тарелке (ВЭТТ) или теоретической ступени (ВЭТС), и (опр-ся по экспериментальным данным); n. Т – число теоретических тарелок (ступеней изменения концентрации). Y, Y* В Yн Рабочая линия Ступени изменения концентрации у1*= у2 Yв С А Линия равновесия О Хв Хн Х Рис. 5. Графическое определение числа ступеней изменения концентрации (теоретических тарелок) в абсорбере. Рис. 6. Схема тарельчатого абсорбера

Химическая абсорбция (хемосорбция) – это абсорбция, при к-рой поглощаемое вещество химически взаимодействует с абсорбентом. К процессам хим. абсорбции относятся моно-этаноламиновая (МЭА), поташная и щелочная очистка газов от СО 2, процессы очистки газов от H 2 S, медноаммиачная очистка от СО и другие процессы. Протекание химической реакции в процессе абсорбции оказывает влияние как на равновесие между фазами, так и на кинетику абсорбции. В этом случае кинетика абсорбции определяется не только скоростью массообмена, но и кинетическими закономерностями реакции. При протекании в жидкой фазе р-ции м. растворённым газообразным компонентом и поглотителем часть компонента переходит в связанное состояние и конц-ция свободного компонента в жидкости понижается. Такое понижение приводит к увеличению концентрационного градиента и ускорению абсорбции в жидкой фазе по сравнению с физ. абсорбцией. Это ускорение тем больше, чем выше скорость хим. реакции.

При высоких скоростях р-ции ускорение абсорбции м. б. настолько большим, что сопротивление жидкой фазы становится равным нулю. Наоборот, при очень медленных р-циях ускорение настолько мало, что им можно пренебречь и рассм-ть процесс как физ. абс-цию. Ускорение абсорбции протекании хим. р-ции в жидкой фазе может быть учтено либо увеличением коэффициента массоотдачи, если принимать движущую силу такой же, как при физ. абсорбции; либо увеличением движущей силы, если принимать коэффициент массоотдачи таким же как при физической абсорбции. Между обоими способами существует зависимость: Wа = βж. I F∆ж = βж. F(∆ж + δ), где βж – коэф-нт массоотдачи в жидкой фазе при физ. абсорбции; βж. I – то же при протекании реакции, отнесённый к движущей силе при физ. абсорбции; ∆ж – движущая сила процесса физ. абсорбции; δ – увеличение движущей силы в жидкой фазе при протекании в ней реакции. Связь коэф-нта массопередачи с коэф-нтами массоотдачи при хемосорбции определяется ур-ми: 1/Ky′ = (1/βг) + (m/βж′);

Отсюда коэффициент ускорения абсорбции χ в жидкой фазе при протекании в ней реакции равен: χ = βж. I/βж = 1+ δ /∆ж. Поглотительная способность р-ра зависит в значит. мере от константы хим. реакции. Зав-сть раств-сти от давления более сложная, чем при физ. абсорбции. Характерная особенность раствсти газов в хемосорбентах заключается в медленном росте р-сти с увнием давления. Чем выше давление, тем медленнее ув-ся р-сть. Теплота растворения при этом велика (до 125 к. Дж/моль), поэтому раств-сть сильно зависит от т-ры. Чем меньше конц-ция растворённого газа, тем больше мольная теплота растворения, поэтому при малых конц-циях газа в регенерированных р-лях давление его над р-ром резко снижается при ум-нии т-ры. Это позволяет достигнуть более тонкой очистки, чем при физ. абсорбции. Ёмкость хемосорбента обычно мало зависит от давления, поэтому хемосорбция более выгодна при небольшой конц-ции примесей в газе, а регенерацию необходимо проводить гл. обр. путем повышения т-ры, а не снижения давления.