Теоретические основы управления и контроля МОДЕЛИРОВАНИЕ ПОТОКОВ РАБОТ

Теоретические основы управления и контроля МОДЕЛИРОВАНИЕ ПОТОКОВ РАБОТ СЕТЯМИ ПЕТРИ

Сети Петри. Введение Сети Петри отражают логическую последовательность событий, позволяют прослеживать потоки информации, отрабатывают взаимодействие процессов. Их преимущество заключается в простоте восприятия человеком и понимания графических образов, в том числе динамических. Сеть Петри представляется графом, узлами которого служат позиции (обозначаемые кружочками) и переходы (обозначаемые черточками или кружочками другого цвета), связанные направленными дугами.

Сети Петри. Введение Сеть Петри формально задаётся пятёркой: N = (P, T, F, H, M 0 ) Где P – непустое конечное множество позиций (мест), T – непустое конечное множество переходов, F и H – матрицы инцидентности, причем: F: P x T – отображение множества P на T, H: T x P – отображение множества T на P, M 0 – начальная разметка (маркировка) – вектор, который содержит информацию о количестве меток (фишек, маркеров) в соответствующих позициях (местах) сети.

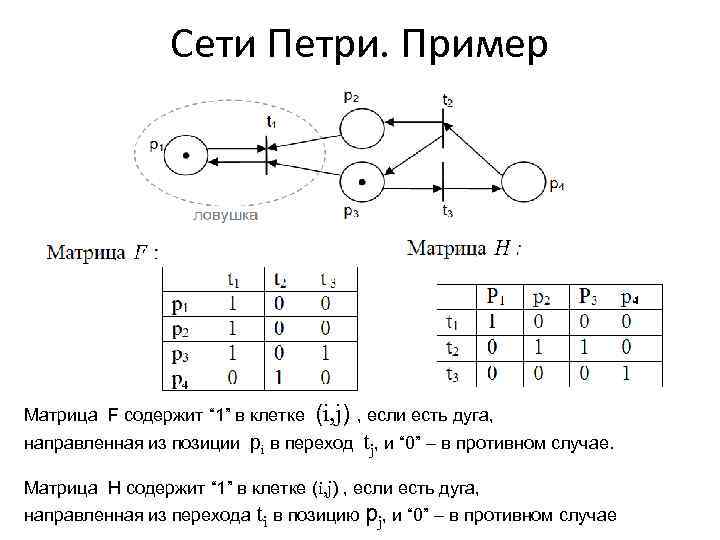
Сети Петри. Пример Матрица F содержит “ 1” в клетке (i, j) , если есть дуга, направленная из позиции pi в переход tj, и “ 0” – в противном случае. Матрица H содержит “ 1” в клетке (i, j) , если есть дуга, направленная из перехода ti в позицию pj, и “ 0” – в противном случае

Сети Петри. Классификация Сеть называется K-ограниченной, если количество меток в позиции не превышает величины K. Сеть является безопасной, если она K-ограничена и K=1. Если метка при попадании в позицию не может ее покинуть при данной разметке, то такая позиция является ловушкой. Сеть находится в состоянии тупика, если дальнейшее срабатывание переходов невозможно

Сети Петри. Классификация Автоматные сети Петри (state machine)- сети у которых переход имеет не более одного входа и не более одного выхода. Такие сети обычно описывают последовательные процессы с ветвлением по условию. Если сеть имеет только одну фишку, то сеть является, по сути, графом автомата, который последовательно переходит из одного состояния в другое. Сеть снабжается одной фишкой (несколькими), расположенной в начальной вершине. Общее число фишек в автоматной сети при переходе от состояния к состоянию не меняется, т. е. SM-сети являются ограниченными, а при наличии одной фишки - безопасными.

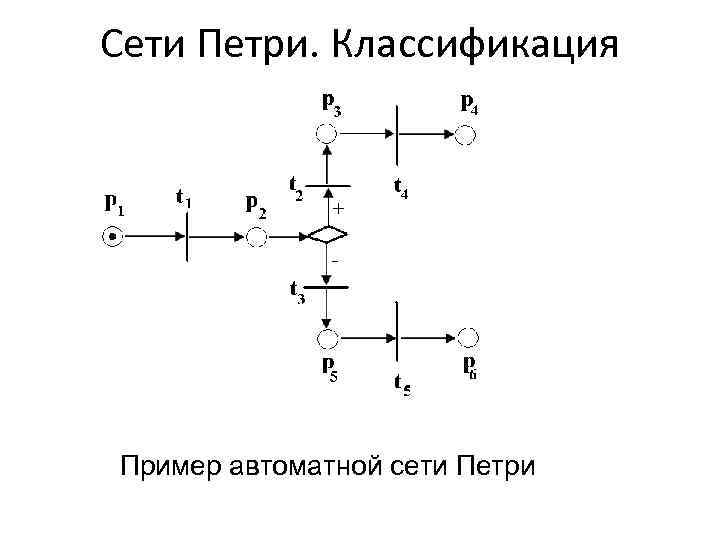
Сети Петри. Классификация Пример автоматной сети Петри

Сети Петри. Классификация Маркированные сети (MG-сети или market graph) - сети, у которых каждая позиция имеет не более одного входа и не более одного выхода. С помощью них моделируют последовательно–параллельные процессы. MG-сети называют также синхрографами. Переход в синхрографе является потенциально живым, если он не входит не в один Пустой Цикл (ПЦ не содержит ни одной фишки). Синхрограф является живым, если каждый его цикл не пуст при начальной разметке. Живой синхрограф является безопасным тогда и только тогда каждая позиция входит в определенный цикл, содержащий ровно одну фишку.

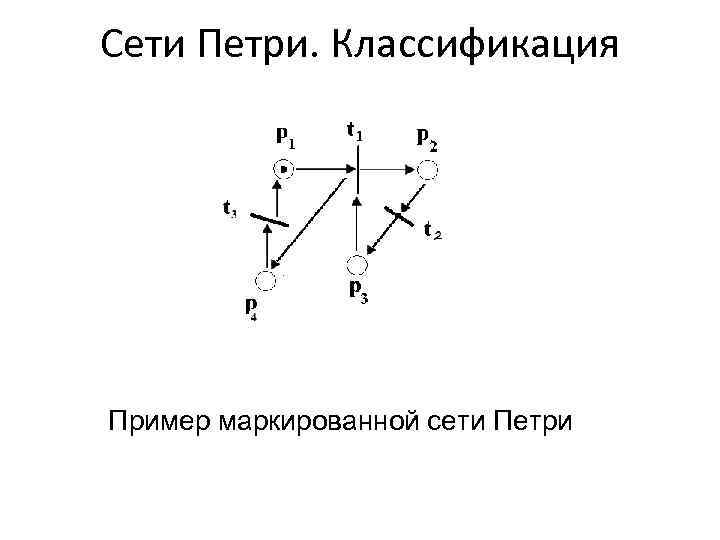
Сети Петри. Классификация Пример маркированной сети Петри

Сети Петри. Классификация Сети свободного выбора (FC-сети или free choice) - сети у которых каждая дуга, выходящая из позиции, является либо единственным выходом из нее, либо единственным входом в переход. FC-сети используются для описания процессов управления. Для сетей свободного выбора разработан механизм выявления ловушек и тупиков. Необходимое условие живости сети свободного выбора является то, что тупики должны содержать в себе ловушки. Простые сети – (SN-сети или Simple nets) - сети, у которых каждый переход может иметь не более одной общей позиции с другими переходами.

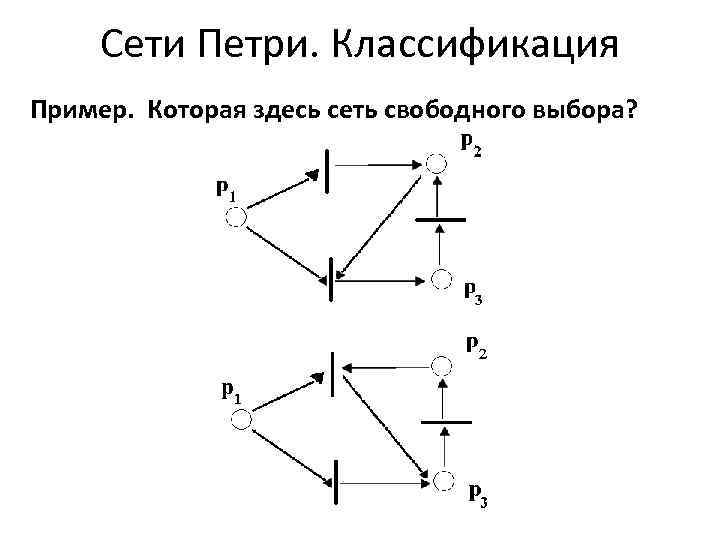
Сети Петри. Классификация Пример. Которая здесь сеть свободного выбора?

Сети Петри. Классификация Ординарные сети – (ON-сети или Ordinary nets) - Сети, которые не имеют ограничений, кроме одного – кратность дуг должна быть не более единицы. Между узлами прокладывается ровно одна связь. Неординарная сеть может быть преобразована в ординарную. Для этого находят максимальную кратность дуг каждого места и производят размножение позиции в соответствие с установленной кратностью. Эти позиции соединяются друг с другом в кольцо, при этом дуги прорезаются своим переходом. Направление дуг является однонаправленным так, чтобы образовывался цикл.

Сети Петри. Классификация Раскрашенные сети – (CPN- сети или Coloured Petri Nets) - сети, у которых каждая метка имеет свой определенный цвет и переход, связанный с некоторым условием, определяющим наличие связанных с ним входных позиций меток определенного цвета. Цвет метки принято обозначать некоторой буквой. С каждым переходом связывается таблица правил его срабатывания. В таблице переходов столбцы слева от разделяющей линии связываются с входными местами переходов и в совокупности содержат сочетание конкретных фишек, при которых переход может сработать. Столбцы, стоящие справа, указывают на признаки или на вид фишек, которые будут переданы выходным местам.

Сети Петри. Классификация Ординарные сети – (ON-сети или Ordinary nets) - Сети, которые не имеют ограничений, кроме одного – кратность дуг должна быть не более единицы. Между узлами прокладывается ровно одна связь. Неординарная сеть может быть преобразована в ординарную. Для этого находят максимальную кратность дуг каждого места и производят размножение позиции в соответствие с установленной кратностью. Эти позиции соединяются друг с другом в кольцо, при этом дуги прорезаются своим переходом. Направление дуг является однонаправленным так, чтобы образовывался цикл.

Сети Петри. Функционирование При заданной начальной разметке проверяется наличие переходов, которые могут сработать. Если такой переход один, то он срабатывает, если несколько – срабатывают один из них случайным образом. После срабатывания перехода, система переходит в новое состояние, определяемое новой разметкой. и так далее. Сеть останавливается в двух случаях: все метки покидают систему; система переходит в тупиковое состояние, из которого нет перехода в другое состояние. Переход является живым при данной разметке , если существует такая последовательность маркирования из , которая приводит к срабатыванию данного перехода. Сеть является живой при данной начальной разметке, если жив каждый её переход. Переход может сработать, только если он “возбужден”. Переход возбужден, если во всех его входных позициях имеется не менее, чем по одной метке.

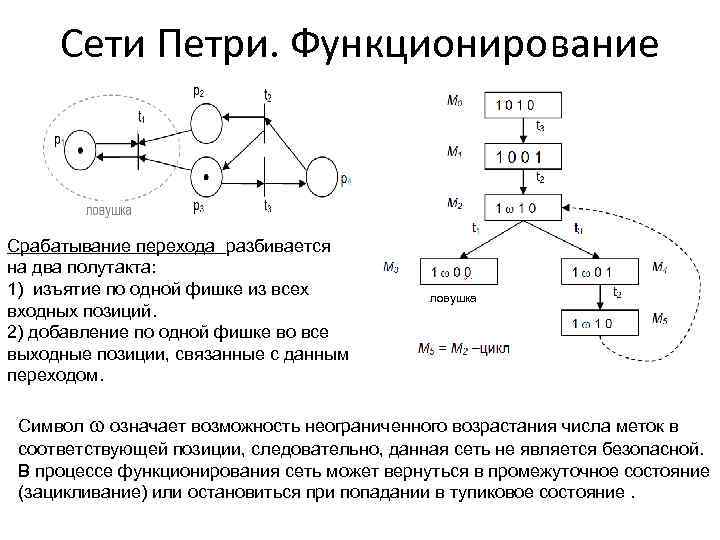
Сети Петри. Функционирование Срабатывание перехода разбивается на два полутакта: 1) изъятие по одной фишке из всех ловушка входных позиций. 2) добавление по одной фишке во все выходные позиции, связанные с данным переходом. Символ означает возможность неограниченного возрастания числа меток в соответствующей позиции, следовательно, данная сеть не является безопасной. В процессе функционирования сеть может вернуться в промежуточное состояние (зацикливание) или остановиться при попадании в тупиковое состояние.

Сети Петри. Алгебраическое описание Смена маркировок сети, т. е. функционирование сети Петри, может быть описано следующим уравнением: Mk = Mk-1 + AT Uk-1 где A = H - FT ; k = 1, 2, … Uk – управляющий вектор в k–ый момент (такт) функционирования сети, размерность которого совпадает с количеством переходов в сети. В начальном состоянии имеем: g 1 причем gj=1 означает готовность перехода tj к g 2 срабатыванию, gj =0 – отсутствие готовности. U = … F: P x T – отображение множества P на T H: T x P – отображение множества T на P gs-1 gs

Сети Петри. Алгебраическое описание Элементы управляющего вектора можно определить следующим образом. Элементы вектора текущей разметки Mj сравниваются с соответствующими элементами столбцов матрицы инцидентности F, каждый из которых отвечает за состояние одного перехода. Если все элементы вектора текущего состояния не меньше соответствующих элементов – i- го столбца матрицы , то это означает возможность срабатывания i-го перехода, и, следовательно, gi=1. В нашем случае: Далее получаем M 1 = M 0 + AT U 0 и определяем Затем процесс повторяется

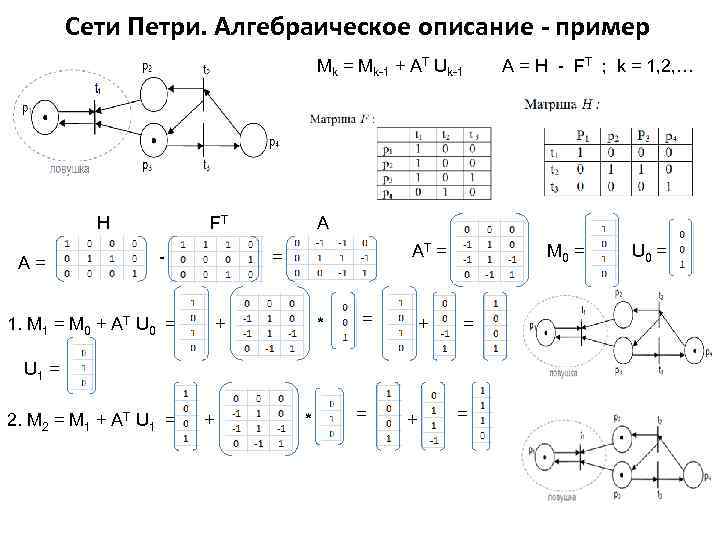
Сети Петри. Алгебраическое описание - пример Mk = Mk-1 + AT Uk-1 A = H - FT ; k = 1, 2, … H FT А - = АT = M 0 = U 0 = А= 1. M 1 = M 0 + AT U 0 = + * = + = U 1 = 2. M 2 = M 1 + AT U 1 = + * = + =