Теоретические основы Основы теории вероятности Распределения случайных величин

Теоретические основы Основы теории вероятности. Распределения случайных величин.

• • Пример. Закон Ома. U = R*I U – напряжение, R сопротивление, I – сила тока При постоянном значении R сопротивления, для каждого значения I определенное значение U (детерминированное явление). U U=R*I I

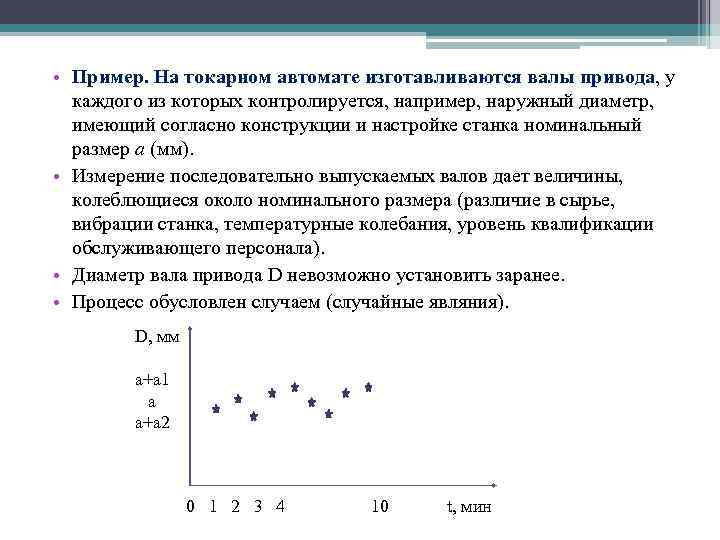• Пример. На токарном автомате изготавливаются валы привода, у каждого из которых контролируется, например, наружный диаметр, имеющий согласно конструкции и настройке станка номинальный размер а (мм). • Измерение последовательно выпускаемых валов дает величины, колеблющиеся около номинального размера (различие в сырье, вибрации станка, температурные колебания, уровень квалификации обслуживающего персонала). • Диаметр вала привода D невозможно установить заранее. • Процесс обусловлен случаем (случайные являния). D, мм а+а 1 а а+а 2 0 1 2 3 4 10 t, мин

Введение • Случайный эксперимент теоретически можно воспроизвести неограниченное число раз. • Т. о. при рассмотрении случайных явлений имеем дело с массовыми явлениями. • В основе массовых явлений лежат некоторые закономерности (хотя исход каждого конкретного испытания предсказать невозможно). • Теория вероятностей изучает эти закономерности.

Что означает слово "вероятность"? • Вероятность (probability) — это возможность наступления некоторого события. • Можно говорить о вероятности того, что из колоды карт будет вынута карта черной масти, что человек предпочтет один продукт другому или что новый продукт, появившийся на рынке, будет пользоваться спросом. • В каждом из этих вариантов вероятность является числовой величиной, лежащей в интервале от 0 до 1 включительно. • Вероятность события, которое никогда не может произойти (невозможное событие), равна 0, а вероятность события, которое происходит постоянно (достоверное событие), равна 1.

В простейшем случае, когда все исходы испытаний равновероятны, их вероятность определяется в соответствии с формулой Вероятность события = • где X — количество испытаний, в которых произошло событие, Т — общее количество испытаний. • Что означает эта вероятность? • Например, в стандартной колоде игральных карт есть 26 карт красной и 26 карт черной масти. Предположим, что после извлечения карта возвращается в колоду. Означает ли это, что из двух извлеченных карт одна обязательно окажется черной масти? Нет, поскольку никто не может предсказать исходы нескольких последовательных испытаний. Однако, если продолжать испытания достаточно долго, количество карт черной масти, извлеченных из колоды, будет приблизительно равно 0, 50.

О Выборочное пространство и события • Основным понятием теории вероятностей является событие. • Событие – это любой возможный результат случайного эксперимента. • Элементарное событие – событие, которое можно описать одной характеристикой • Совокупность всех элементарных событий называется выборочным пространством или пространством исходов • Дополнением события А называются все события, которые не являются частью события А (A’) • Совместное событие – это событие которое имеет несколько характеристик

• Существует несколько способов изучения выборочного пространства • Мы рассмотрим метод, основанный на таблице перекрестной классификации (таблица сопряженности признаков)

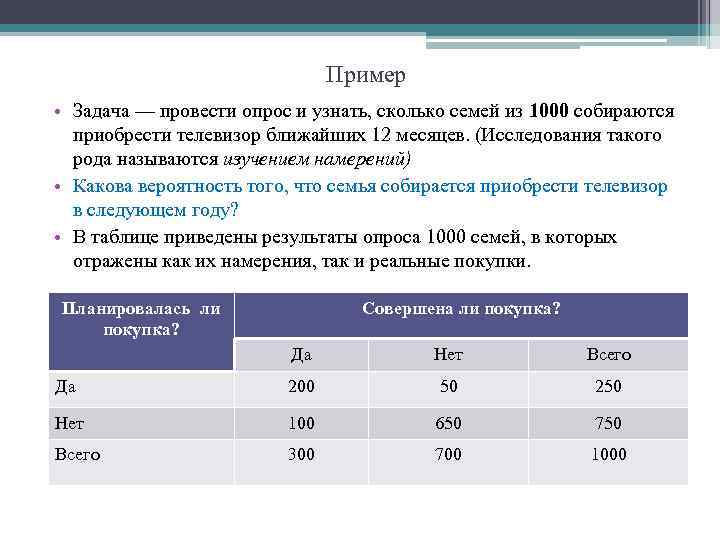Пример • Задача — провести опрос и узнать, сколько семей из 1000 собираются приобрести телевизор ближайших 12 месяцев. (Исследования такого рода называются изучением намерений) • Какова вероятность того, что семья собирается приобрести телевизор в следующем году? • В таблице приведены результаты опроса 1000 семей, в которых отражены как их намерения, так и реальные покупки. Планировалась ли покупка? Совершена ли покупка? Да Нет Всего Да 200 50 250 Нет 100 650 750 Всего 300 700 1000

В данном примере пространство элементарных событий состоит из 1 000 семей. Элементарные события, принадлежащие выборочному пространству, классифицируются в зависимости от разновидности исхода. Например, если нас интересуют планы семей, события формулируются так: "покупка планируется" и "покупка не планируется". Таким образом, способ, которым разбивается выборочное пространство, зависит от вида оцениваемой вероятности.

• Так, в таблице дополнением события "покупка планируется" является событие "покупка не планируется". • Кроме того, событие "покупка планируется и покупка совершена" является совместным, поскольку оно состоит из двух элементарных событий — "покупка планируется" и "покупка совершена".

Правила вычисления вероятностей • Вероятность должна лежать в интервале от 0 до 1 • Вероятность невозможного события равна 0 • Вероятность достоверного события равна 1 • Вероятность элементарного события А называется безусловной (simple probability) и обозначается как Р(А).

Безусловная вероятность • Например, безусловной является вероятность события "покупка планируется". • Для того чтобы вычислить вероятность этого события, следует применить формулу Таким образом, вероятность того, что отдельная семья планирует покупку широкоэкранного телевизора, равна 0, 25 (25%).

Вероятность совместных событий • Совместное событие состоит из одновременных элементарных событий. • В таблице указано количество семей, которые планировали купить и действительно купили широкоэкранный телевизор. • Поскольку эта группа состоит из 200 семей, вероятность события "покупка планировалась и осуществилась" вычисляется по следующей формуле.

• С помощью понятия вероятности совместного события можно иначе определить безусловную вероятность элементарного исхода. • Безусловная вероятность элементарного события Где события В 1, В 2, …, Вk являются взаимоисключающими и исчерпывающими. • Два события называются взаимоисключающими, если они не могут происходить одновременно. • Множество событий называется исчерпывающим, если происходит хотя бы одно из них. Например, события "человек является мужчиной" и "человек является женщиной" являются взаимоисключающими и исчерпывающими. Эти события никогда не происходят одновременно, и в то же время человек всегда является либо мужчиной, либо женщиной.

Безусловная вероятность элементарного события

Общее правило сложения вероятностей • Зная вероятности события А и события «А и В» , можно вычислить вероятность события «А или В» Вычисление вероятности события «А или В» подчиняется общей формуле сложения вероятности

Правило сложения вероятностей взаимоисключающих событий Пример 300 семей ответили, где они совершили покупку Какова вероятность того, что случайно выбранная семья, купившая телевизор, заказала его через интернет или по почте?

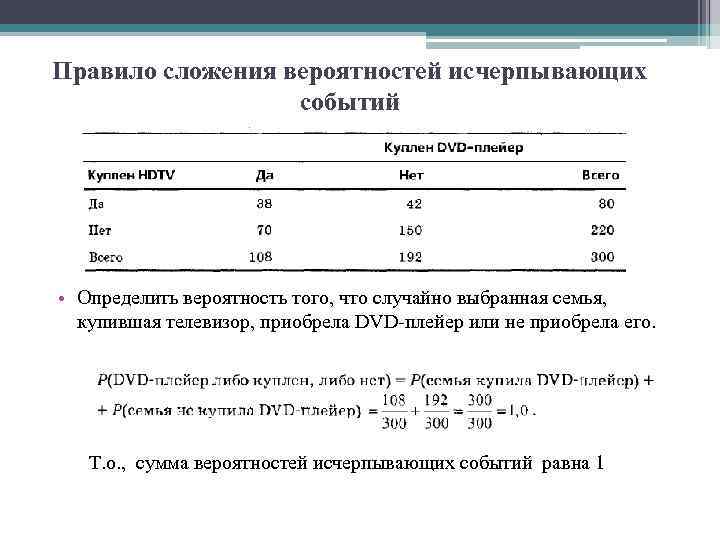Правило сложения вероятностей исчерпывающих событий • Определить вероятность того, что случайно выбранная семья, купившая телевизор, приобрела DVD плейер или не приобрела его. Т. о. , сумма вероятностей исчерпывающих событий равна 1

Условная вероятность • Как определить вероятность события, если известна некоторая информация о событиях, происшедших до него? • Вероятность события А, при вычислении которой учитывается информация о событии В, называется условной и обозначается как • Вероятность события А при условии, что наступило событие В, равна вероятности события «А и В» , деленной на вероятность события В • Вероятность события В при условии, что наступило событие А, равна вероятности события «А и В» , деленной на вероятность события А

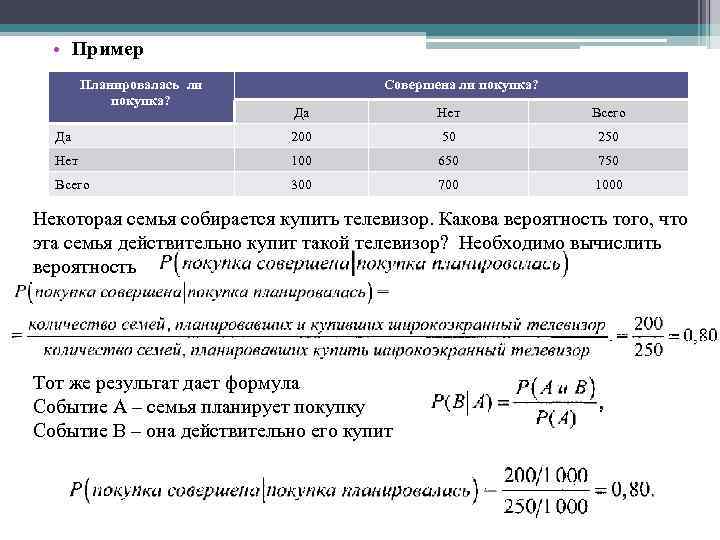• Пример Планировалась ли покупка? Совершена ли покупка? Да Нет Всего Да 200 50 250 Нет 100 650 750 Всего 300 700 1000 Некоторая семья собирается купить телевизор. Какова вероятность того, что эта семья действительно купит такой телевизор? Необходимо вычислить вероятность Тот же результат дает формула Событие А – семья планирует покупку Событие В – она действительно его купит

Статистическая независимость • Вероятность того, что случайно выбранная семья приобрела телевизор при условии, что она планировала это сделать, равна 200/250 = 0, 80 • Безусловная вероятность того, что случайно выбранная семья приобрела телевизор, равна 300/ 1000 = 0, 30 • Априорная информация о том, что семья планировала покупку влияет на вероятность самой покупки – эти события зависят друг от друга. • В противоположность этому, существуют статистически независимые события, вероятности появления которых не зависят друг от друга.

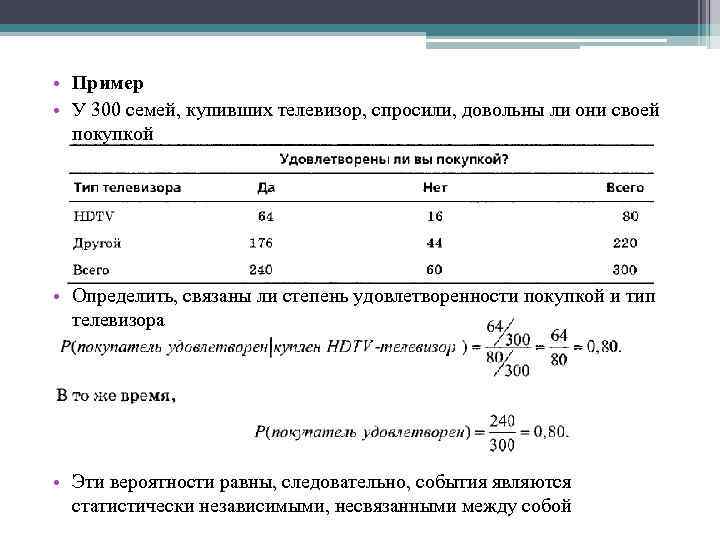• Пример • У 300 семей, купивших телевизор, спросили, довольны ли они своей покупкой • Определить, связаны ли степень удовлетворенности покупкой и тип телевизора • Эти вероятности равны, следовательно, события являются статистически независимыми, несвязанными между собой

Правило умножения вероятностей

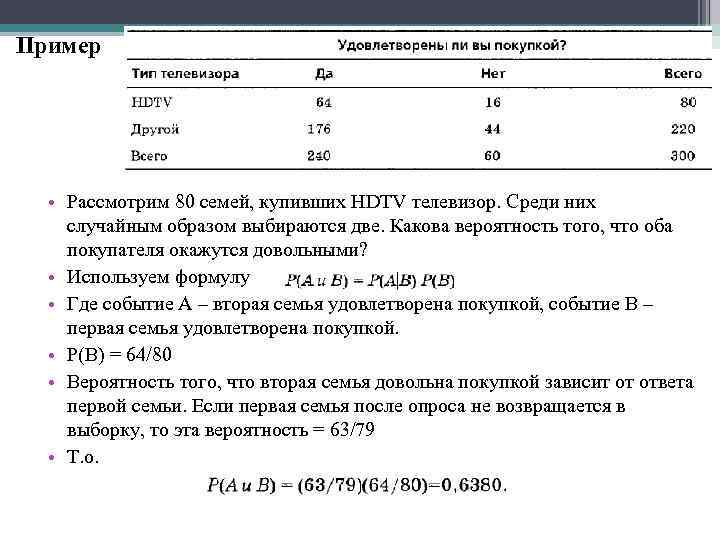Пример • Рассмотрим 80 семей, купивших HDTV телевизор. Среди них случайным образом выбираются две. Какова вероятность того, что оба покупателя окажутся довольными? • Используем формулу • Где событие А – вторая семья удовлетворена покупкой, событие В – первая семья удовлетворена покупкой. • Р(В) = 64/80 • Вероятность того, что вторая семья довольна покупкой зависит от ответа первой семьи. Если первая семья после опроса не возвращается в выборку, то эта вероятность = 63/79 • Т. о.

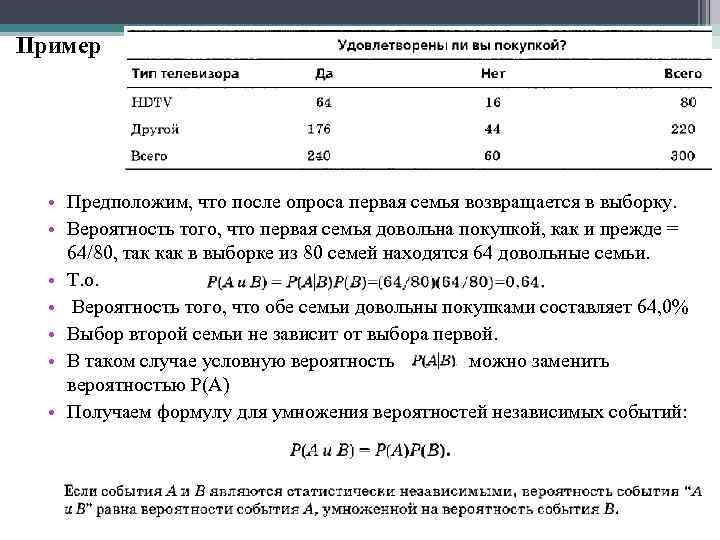Пример • Предположим, что после опроса первая семья возвращается в выборку. • Вероятность того, что первая семья довольна покупкой, как и прежде = 64/80, так как в выборке из 80 семей находятся 64 довольные семьи. • Т. о. • Вероятность того, что обе семьи довольны покупками составляет 64, 0% • Выбор второй семьи не зависит от выбора первой. • В таком случае условную вероятность можно заменить вероятностью Р(А) • Получаем формулу для умножения вероятностей независимых событий:

• Можно модифицировать формулу для вычисления безусловной вероятности события А • Безусловная вероятность элементарного события:

Теорема Байеса • Условная вероятность события учитывает информацию о том, что произошло некоторое другое событие. • Этот подход можно использовать для уточнения вероятности с учетом вновь поступившей информации и для вычисления вероятности того. Что наблюдаемый эффект является следствием некоторой конкретной причины. • Процедура уточнения этих вероятностей называется теоремой Байеса. Была разработана Томасом Байесом в 18 веке.

Правила счета •

• Второе правило счета обобщает первое и допускает ситуации, когда количество возможных исходов изменяется от испытания к испытанию. • Например, ГАИ заинтересовалась, сколько автомобильных номеров можно составить из 3 букв и 3 цифр. • Каждая из букв порождает 33 исхода, каждая из цифр – 10 Т. о. количество автомобильных номеров, которое можно составить из 3 букв и 3 цифр = 33*33*33*10*10*10 = 35937000

• Третье правило счета позволяет вычислить количество способов, которыми можно упорядочить заданный набор объектов. • Например, нужно расставить на полке 6 книг. Количество способов, которым можно упорядочить 6 книг равно 6! = 6 х5 х4 х3 х2 х1=720

• Четвертое правило счета • Во многих задачах нужно знать количество способов, которым можно упорядочить подмножество, принадлежащее определенной группе объектов. • Каждый вариант упорядочения называется перестановкой. • Пусть на полке помещаются только 4 книги. Сколько существует способов расставить книги на полке, если общее количество книг равно 6? • Следовательно:

• Пятое правило счета • Бывают ситуации, когда порядок следования объектов не важен, а учитывается лишь количество вариантов извлечения Х объектов из совокупности, состоящей из n объектов. Это правило называется сочетанием. • Т. о. общее количество комбинаций 4 книг, извлеченных из совокупности, состоящей из 6 книг:

Законы распределения дискретных случайных величин

• В теории вероятности и математической статистике случайные события связывают с числами. • Возникает новое понятие – случайная величина (случайная переменная)

• Пример • Диаметры валов колеблются около номинального размера а=35 мм. • Событие А: диаметр попадает в пределы поля допуска [34, 995; 35, 011] или A={34, 995≤D≤ 35, 011} • Случайное событие А можно охарактеризовать множеством действительных чисел, расположенных между Тн=34, 995 и Тв=35, 011 • Наступление этого события равнозначно попаданию диаметра вала D в интервал [34, 995; 35, 011] • Следовательно со случайным событием А сопоставляется случайная величина X, которая при наступлении события А случайным образом принимает некоторое значение в числовом интервале [34, 995; 35, 011]. В этом случае можно записать А={x 1≤X≤x 2} Где х1 = 34, 995 и х2 = 35, 011

•

Случайная величина • Случайная величина Х называется дискретной, если она может принимать конечное или счетное число различных значений х1, х2, х3…. . • Пример • При подсчете числа простоев станка за смену (0, 1, 2 …. ) • При регистрации числа вызовов на телефонной станции в течении промежутка времени • При подсчете количества единиц транспорта на перекрестке в определенное время дня

• Непрерывная случайная величина обладает следующим свойством: она может принимать любые значения в определенном интервале числовой оси. • Примеры непрерывных случайных величин можно найти при рассмотрении почти всех процессов измерения в технике (измерение размеров, физических свойств и др. )

• Распределение дискретной случайной величины – это исчерпывающий список всех возможных значений случайной переменной, где каждому исходу поставлена в соответствие его вероятность

Распределение количества ипотечных займов, выданных за неделю Количество ипотечных займов, выданных за неделю Вероятность 0 0, 10 1 0, 10 2 0, 20 3 0, 30 4 0, 15 5 0, 10 6 0, 05

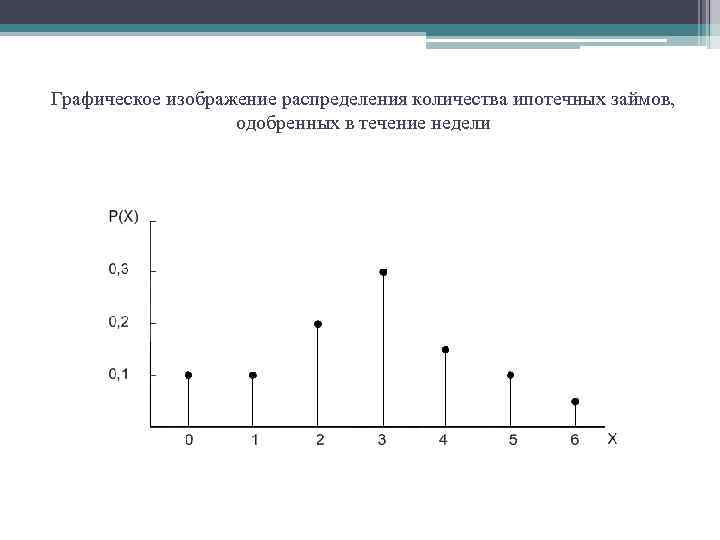Графическое изображение распределения количества ипотечных займов, одобренных в течение недели

Функция распределения • Один из способов задания случайной величины – с помощью функции распределения – вероятности того, что случайная величина X окажется меньше некоторого значения x. • F(x)=P(X

• Т. о. случайная величина Х – это величина, которая при любом испытании случайным образом принимает определенное действительное числовое значение и обладает функцией распределения, определенной как F(x)=P(X

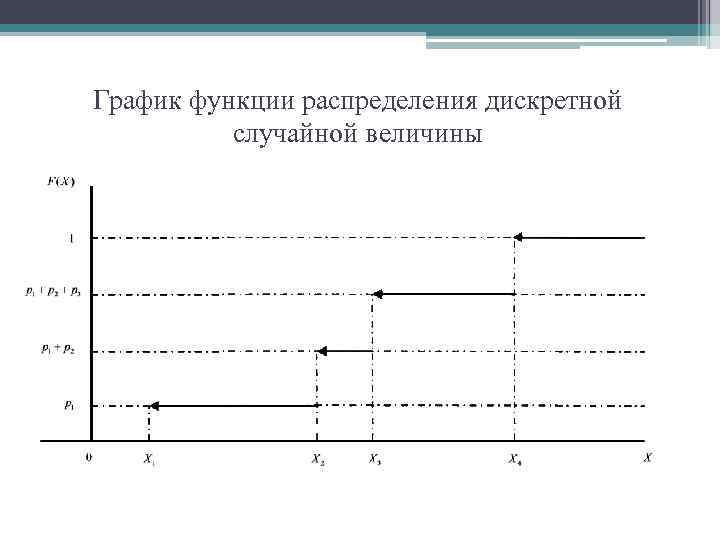График функции распределения дискретной случайной величины

Свойства функции распределения Отметим основные свойства функции распределения: её значения лежат в промежутке от 0 до 1 F( ∞) = 0, F(∞)=1. Функция F(x) – монотонно неубывающая: при x 2>x 1, F(x 2)>=F(x 1). Вероятность попадания случайной величины в полуинтервал [x 1, x 2) определяется по формуле: P(x <=X

Математическое ожидание дискретной случайной величины • Математическим ожиданием μ (expected value) дискретной случайной величины X называется среднее значение ее распределения. Эта величина равна сумме произведений всех значений случайной величины X на соответствующие вероятности Р(Х). • Математическое ожидание дискретной случайной величины X — это взвешенное среднее (weighted value) всех возможных исходов, где в качестве весов служат вероятности каждого исхода.

Математическое ожидание дискретной случайной величины где Xi – i е значение дискретной случайной величины Х, Р(Хi) – вероятность i го значения дискретной случайной величины Х Математическое ожидание количества ипотечных займов, выданных за неделю, вычисляется по следующей формуле

Дисперсия дискретной случайной величины

Стандартное отклонение дискретной случайной величины • Дисперсия и стандартное отклонение количества ипотечных займов, выданных за неделю, вычисляются по следующим формулам

Закон распределения • Законом распределения случайной величины называется всякое соответствие между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения случайной величины может быть задан в виде таблицы, функции распределения и плотности распределения.

Биномиальное распределение • Если задача позволяет явно записать математическое выражение, представляющее случайную величину, можно вычислить точную вероятность любого ее значения. В этом случае можно вычислить и перечислить все значения функции распределения. • Биномиальное распределение используется для оценки количества успехов в выборке, состоящей из n наблюдений. • Таким образом, случайная величина, подчиняющаяся биномиальному закону распределения, принимает значения от 0 до n.

Свойства биномиального распределения Биномиальное распределение используется для моделирования ситуаций, характеризующихся следующими особенностями. • Выборка состоит из фиксированного числа элементов n, представляющих собой исходы некоего испытания. • Каждый элемент выборки принадлежит одной из двух взаимоисключающих категорий, исчерпывающих все выборочное пространство. Как правило, эти две категории называют успех и неудача. • Вероятность успеха р является постоянной. Следовательно, вероятность неудачи равна 1 р. • Исход (т. е. удача или неудача) любого испытания не зависит от результата другого испытания. • Чтобы гарантировать независимость исходов, элементы выборки, как правило, получают с помощью двух разных методов. Каждый элемент выборки случайным образом извлекается из бесконечной генеральной совокупности без возвращения или из конечной генеральной совокупности с возвращением.

Пример • Заполняется документ. Затем информационная система проверяет, нет ли в нем ошибок, а также неполной или недостоверной информации. • Предварительные данные свидетельствуют, что вероятность ошибок в заказах равна 0, 10. • Компания хотела бы знать, какова вероятность обнаружить определенное количество ошибочно заполненных документов выборке. • Например, заполнили четыре электронных формы. Какова вероятность, что все они окажутся с ошибками? • Как вычислить эту вероятность?

• Под успехом в будем понимать ошибку при заполнении документа, а все остальные исходы будем считать неудачей. Напомним, что нас интересует количество ошибочно заполненных форм в заданной выборке. • Какие исходы мы можем наблюдать? Если выборка состоит из четырех бланков, ошибочными могут оказаться один, два, три или все четыре, кроме того, все они могут оказаться правильно заполненными. • Может ли случайная величина, описывающая количество неправильно заполненных форм, принимать какое либо иное значение? Это невозможно, поскольку количество неправильно заполненных форм не может превышать объем выборки n или быть отрицательным. • Таким образом, случайная величина, подчиняющаяся биномиальному закону распределения, принимает значения от 0 до n.

Пример Допустим, что в выборке из четырех бланков соблюдаются следующие исходы Первый Второй Третий Четвертый Ошибочный Правильный Ошибочный Какова вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех бланков, причем в указанной последовательности? Поскольку предварительные исследования показали, что вероятность ошибки при заполнении формы равна 0, 10 вероятности указанных выше исходов вычисляются следующим образом Первый Второй Третий Четвертый р=0, 10 1 р=0, 90 р=0, 10 Поскольку исходы не зависят друг от друга вероятность указанной последовательности исходов равна

Если же необходимо вычислить количество вариантов выбора X объектов из выборки, содержащей n элементов, следует воспользоваться формулой Количество вариантов выбора X объектов из выборки, содержащей n элементов, определяется по формуле Сочетания Где n!=1*2*…*n факториал числа n, причем 0!=1 и 1!=1. Если n=4 b X=3, количество последовательностей, состоящих из трех элементов, извлеченных из выборки, объем которой равен 4, определяется по формуле

Рассмотрим вероятности каждой последовательности. Последовательность 1= ошибочный, правильный Последовательность 2= ошибочный, правильный, ошибочный Последовательность 3= ошибочный, правильный, ошибочный Последовательность 4= правильный, ошибочный, ошибочный Следовательно, вероятность обнаружить три ошибочных бланка вычисляется следующим образом. (Количество возможных последовательностей)*(вероятность конкретной последовательности) = 4*0, 0009 = 0, 0036

Однако при увеличении объема выборки n определить вероятность конкретной последовательности исходов становится труднее. • При заданном количестве испытаний n и вероятности успеха р вероятность последовательности, состоящей из X успехов, равна

1 Вычисление P(X=3) n=4 p=0, 1 Какова вероятность что из 4 заполненных форм 3 окажутся ошибочными? 2 Вычисление P(X≥ 3) n=4 p=0, 1 Какова вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными? Как показано в примере 1, вероятность того, что среди четырех заполненных форм три окажутся ошибочными, равна 0, 0036. Чтобы вычислить вероятность того, что среди четырех заполненных форм не менее трех будут неправильно заполнены, необходимо сложить вероятность того, что среди четырех заполненных форм три окажутся ошибочными, и вероятность того, что среди четырех заполненных форм все окажутся ошибочными. Вероятность второго события равна

• Таким образом, вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными, равна Следовательно, шансы, что среди четырех заполненных форм найдутся не менее трех ошибочных, равны 0, 37%. 3 Вычисление Р (Х< 3) при условии, что n = 4 и р= 0, 1 Допустим, что вероятность неверно заполнить форму равна 0, 1. Какова вероятность того, что среди четырех заполненных форм менее трех окажутся ошибочными Вероятность этого события равна

• Вычислим каждую из этих вероятностей Следовательно, Р(Х < 3) = 0, 6561+0, 2916+0, 0486 = 0, 9963. Вероятность Р(Х < 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х> 3. Тогда Р(Х < 3) = 1 Р(Х > 3) = 1 0, 0037 = 0, 9963.

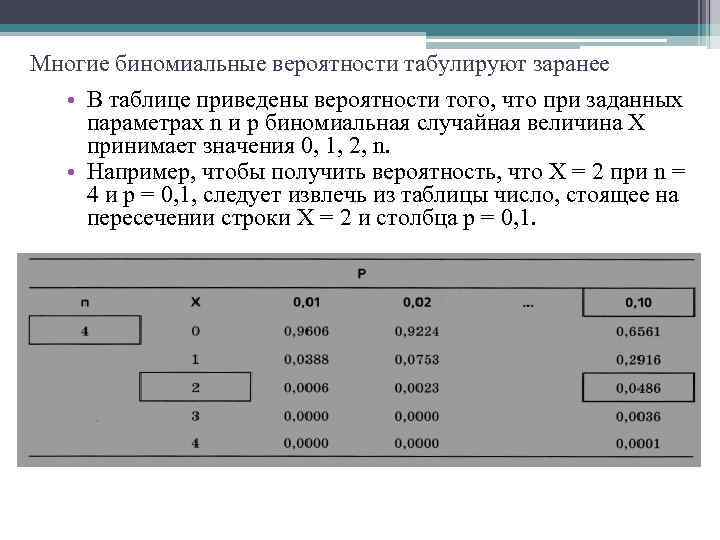Многие биномиальные вероятности табулируют заранее • В таблице приведены вероятности того, что при заданных параметрах n и р биномиальная случайная величина X принимает значения 0, 1, 2, n. • Например, чтобы получить вероятность, что X = 2 при n = 4 и р = 0, 1, следует извлечь из таблицы число, стоящее на пересечении строки Х = 2 и столбца р = 0, 1.

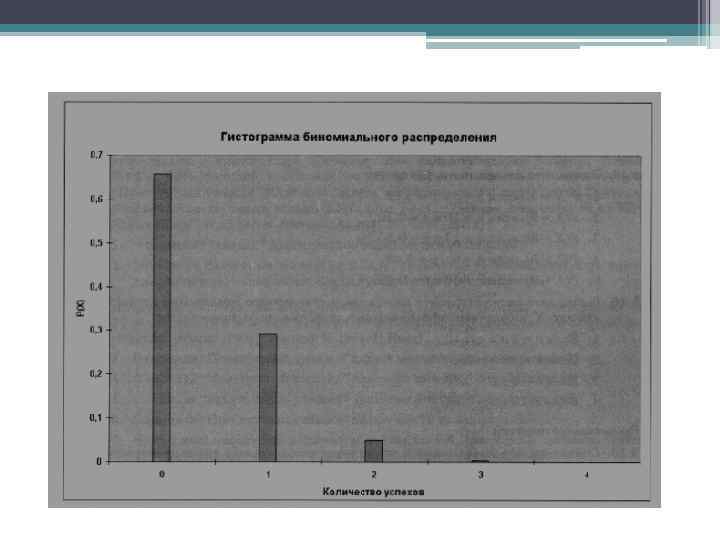
• Свойства биномиального распределения • Биномиальное распределение зависит от параметров n и р. • Форма распределения. Биномиальное распределение может быть как симметричным, так и асимметричным. Если р = 0, 5, биномиальное распределение является симметричным независимо от величины параметра п. Однако, если р ≠ 0, 5, распределение становится асимметричным. Чем ближе значение параметра р к 0, 5 и чем больше объем выборки n, тем слабее выражена асимметрия распределения. • Таким образом, распределение количества неправильно заполненных форм смещено вправо, поскольку р = 0, 1. • На рисунке изображена гистограмма биномиального распределения при n = 4 и р = 0, 1.

Математическое ожидание • Математическое ожидание биномиального распределения равно произведению параметров n и р.

Стандартное отклонение Например, стандартное отклонение количества неверно заполненных форм равно

Гипергеометрическое распределение • Гипергеометрическое распределение, как и биномиальное, позволяет оценить количество успехов в серии из n испытаний. • Разница между ними заключается лишь в способе получения исходных данных. • В биномиальной модели данные выбираются либо из конечной генеральной совокупности с возвращением либо из бесконечной генеральной совокупности без возвращения. • В гипергеометрической модели данные извлекаются только из конечной генеральной совокупности без возвращения. • Таким образом, в то время как в биномиальной модели вероятность успеха р остается постоянной, а испытания не зависят друг от друга, в гипергеометрической модели эти условия не выполняются. Наоборот, в гипергеометрической модели каждый исход зависит от предыдущих исходов.

Гипергеометрическое распределение, описывающее вероятность X успехов при заданных параметрах n, N и А, задается формулой • где Р(Х) — вероятность X успехов при заданных n, N и А, n — объем выборки, N —объем генеральной совокупности, А — количество успешных исходов в генеральной совокупности, N А — количество неудачных исходов в генеральной совокупности, X —количество успехов в выборке, n X — количество неудачных исходов в выборке. • Количество успехов X в выборке не может превосходить количество успехов А в генеральной совокупности либо объем выборки n. Таким образом, диапазон значений, которые может принимать случайная величина, подчиняющаяся гипергеометрическому распределению, ограничен либо объемом выборки (как и диапазон биномиальной переменной), либо объемом генеральной совокупности.

Математическое ожидание гипергеометрического распределения вычисляется по формуле Стандартное отклонение гипергеометрического распределения вычисляется по формуле Выражение называется поправочным коэффициентом конечной генеральной совокупности. Он необходим, поскольку элементы выборки извлекаются из конечной генеральной совокупности.

Пример • Предположим, что некая организация пытается создать группу из 8 человек, обладающих определенными знаниями о производственном процессе. • В организации работают 30 сотрудников, обладающих необходимыми знаниями, причем 10 из них работают в конструкторском бюро. • Какова вероятность того, что в группу попадут два сотрудника из конструкторского бюро, если членов группы выбирают случайно? • Объем генеральной совокупности в этой задаче равен N = 30, объем выборки п = 8, а количество успехов А =10. Таким образом, вероятность того, что в группу попадут два сотрудника из конструкторского бюро, равна 0, 298 (или 29, 8%).

Пример гипергеометрического распределения Из партии объемом N=500 валов привода произвольно отбирается n=50 валов, у которых контролируется диаметр. Если диаметр укладывается в пределы заданного допуска, то вал считается годным, в противном случае изделие бракуется. Из предварительных исследований видно, что в среднем 2% изготовленных валов представляют собой брак. Какова вероятность того, что среди 50 отобранных валов не окажется ни одного дефектного? • N=500 – объем партии; • n=50 – число отобранных изделий; • p=0, 02=А/500 – доля брака; • А=10 – число бракованных изделий; • Х=0 – число дефектных изделий в выборке.

Распределение Пуассона Пуассоновский процесс (Poisson process) возникает в ситуациях, обладающих следующими свойствами. • Нас интересует, сколько раз происходит некое событие в заданной области возможных исходов случайного эксперимента. Область возможных исходов (area of opportunity)может представлять собой интервал времени, отрезок, поверхность и т. п. • Вероятность данного события одинакова для всех областей возможных исходов. • Количество событий, происходящих в одной области возможных исходов, не зависит от количества событий, происходящих в других областях. • Вероятность того, что в одной и той же области возможных исходов данное событие происходит больше одного раза, стремится к нулю по мере уменьшения области возможных исходов.

Пример • предположим, что мы исследуем количество клиентов, посещающих отделение банка, расположенное в центральном деловом районе с 12 до 13 часов. • Предположим, требуется определить количество клиентов, приходящих за одну минуту. • Во первых, событие, которое нас интересует, представляет собой приход клиента, а область возможных исходов — одноминутный интервал. Сколько клиентов придет в банк за минуту— ни одного, один, два или больше? • Во вторых, разумно предположить, что вероятность прихода клиента на протяжении минуты одинакова для всех одноминутных интервалов. • В третьих, приход одного клиента в течение любого одноминутного интервала не зависит от прихода любого другого клиента в течение любого другого одноминутного интервала. • И, наконец, вероятность того, что в банк придет больше одного клиента стремится к нулю, если временной интервал стремится к нулю, например, становится меньше 0, 01 с. • Итак, количество клиентов, приходящих в банк с 12 до 13 часов в течение одной минуты, описывается распределением Пуассона.

• где Р(Х) — вероятность X успешных испытаний, λ — ожидаемое количество успехов, е— основание натурального логарифма, равное 2, 71828, X— количество успехов в единицу времени.

• Допустим, что в течение обеденного перерыва в среднем в банк приходят три клиента в минуту. Какова вероятность того, что в данную минуту в банк придут два клиента? А чему равна вероятность того, что в банк придут более двух клиентов? • Применим формулу с параметром λ = 3. Тогда вероятность того, что в течение данной минуты в банк придут два клиента, равна Вероятность того, что в банк придут более двух клиентов, равна

• Поскольку сумма всех вероятностей должна быть равной 1, члены ряда, стоящего в правой части формулы, представляют собой вероятность дополнения к событию X < 2. Иначе говоря, сумма этого ряда равна 1 Р(Х< 2). Таким образом Теперь получаем ответ Таким образом, вероятность того, что в банк в течение минуты придут не больше двух клиентов, равна 0, 4232 (или приблизительно 42, 3%). Следовательно, вероятность того, что в банк в течение минуты придут больше двух клиентов, равна 0, 5768 (или приблизительно 57, 7%).

Вероятность того, что в заданную минуту в банк придут два клиента, если в среднем в банк приходят три клиента в минуту, находится в таблице на пересечении строки X = 2 и столбца X = 3. Таким образом, она равна 0, 2240.

• Распределение Пуассона вытекает из биноминального распределения, если n стремится к бесконечности, а np=λ остается постоянным. Таким образом, • Это формулировка предельной теоремы Пуассона. • Так как в силу того что вероятность р исследуемого события становится очень мала, то распределение Пуассона называют так же распределением редких событий. • В силу своих свойств Распределение Пуассона находит применение в статистическом контроле качества.

АППРОКСИМАЦИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПОМОЩЬЮ РАСПРЕДЕЛЕНИЯ ПУАССОНА • Если число n велико, а число р — мало, биномиальное распределение можно аппроксимировать с помощью распределения Пуассона. Чем больше число n и меньше число р, тем выше точность аппроксимации. Для аппроксимации биномиального распределения используется следующая модель Пуассона. • где Р(Х) — вероятность X успехов при заданных параметрах n и р, n — объем выборки, р — истинная вероятность успеха, е — константа Эйлера, приближенно равная 2, 71828, X — количество успехов в выборке (X = 0, 1, 2, n). • Случайная величина, имеющая распределение Пуассона, принимает значения от 0 до ∞. Когда распределение Пуассона применя ется для приближения биномиального распределения, количество успехов среди п наблюдений — не может превышать число п.

ПРИБЛИЖЕНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ АППРОКСИМАЦИЯ СТАНДАРТНОГО ОТКЛОНЕНИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Пример Предположим, что 8% шин, произведенных на некотором заводе, являются брако ванными. Чтобы проиллюстрировать применение распределения Пуассона для аппрок симации биномиального распределения, вычислим вероятность обнаружить одну де фектную шину в выборке, состоящей из 20 шин. Применим формулу Если бы мы могли вычислить истинное биномиальное распределение, а не его при ближение, то получили бы следующий результат

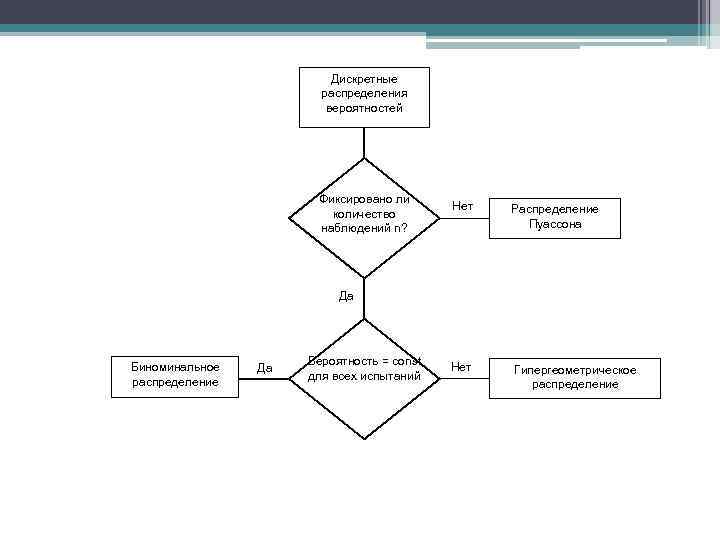Дискретные распределения вероятностей Фиксировано ли количество наблюдений n? Нет Распределение Пуассона Нет Гипергеометрическое распределение Да Биноминальное распределение Да Вероятность = const для всех испытаний

Нормальное и другие непрерывные распределения

• Числовые случайные величины могут быть либо дискретными, либо непрерывными. • Непрерывные случайные величины возникают в результате измерений, результатом которых может являться любая величина, принадлежащая числовой оси или интервалу. • Примером такой случайной величины может служить вес какой нибудь коробки, время загрузки Web страницы, расходы на рекламу, доходы от продажи, время обслуживания клиента и время между двумя приходами клиентов в банк.

Функция распределения непрерывной случайной величины • Функция распределения непрерывной случайной величины обладает теми же свойствами, кроме того она непрерывна и дифференцируема • Часто непрерывная случайная величина задается с помощью производной от функции распределения, которая называется плотностью распределения вероятности

• Закон распределения непрерывной случайной величины полностью определяется ее плотностью. Очевидно понятие плотности распределения, в отличие от функции распределения, справедливо только для непрерывной величины. • График функции f(x) называется кривой распределения. • При известной плотности распределения функция распределения вычисляется как интеграл

Основные свойства плотности распределения • плотность распределения неотрицательна (кривая распределения всегда лежит в верхней полуплоскости) • площадь, ограниченная кривой распределения и осью абсцисс, равна единице (условие нормировки) • вероятность попадания случайной величины в промежуток [х1, х2) равна: (это площадь криволинейной трапеции, заключенной между точками х, и х2) а вероятность того, что непрерывная случайная величина примет конкретное значение х0, равна нулю:

Математическое ожидание непрерывной случайной величины • математическое ожидание — это среднее значение, около которого группируются все значения случайной величины. Свойства математического ожидания: математическое ожидание постоянной равно этой постоянной; постоянный множитель можно вынести из под знака математического ожидания; математическое ожидание суммы случайных величин равно сумме их математических ожиданий.

Дисперсия непрерывной случайной величины • Основные свойства дисперсии: • дисперсия постоянной равна нулю; • постоянный множитель можно выносить из под знака дисперсии, возводя его в квадрат; • для независимых случайных величин дисперсия суммы равна сумме дисперсий. • Среднеквадратичное, или стандартное, отклонение случайной величины — это положительное значение квадратного корня из дисперсии

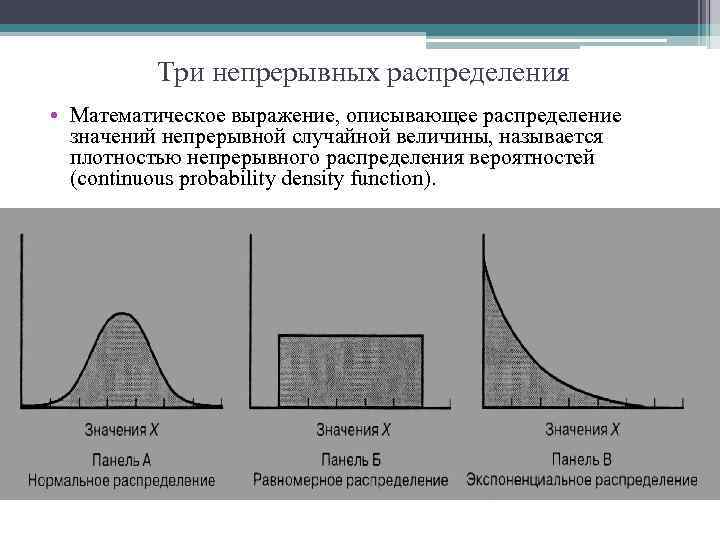Три непрерывных распределения • Математическое выражение, описывающее распределение значений непрерывной случайной величины, называется плотностью непрерывного распределения вероятностей (continuous probability density function).

• На рисунке А представлена плотность нормального распределения. Эта функция является симметричной и колообразной. Следовательно, большинство значений такой случайной величины концентрируется вокруг математического ожидания, которое совпадает с медианой. Несмотря на то что нормально распределенная случайная величина может принимать любые числовые значения, вероятность очень больших положительных или отрицательных значений крайне мала. • На рисунке Б изображена плотность равномерного распределения. Значения случайной величины, равномерно распределенной на интервале от а до b, равновероятны. Иногда это распределение называют прямоугольным. Оно является симметричным, и, следовательно, его математическое ожидание равно медиане. • На рисунке В показана плотность экспоненциального распределения. Это распределение имеет ярко выраженную положительную асимметрию, и, следовательно, его математическое ожидание больше медианы. Экспоненциально распределенные случайные величины изменяются от нуля до плюс бесконечности, однако очень большие значения крайне мало вероятны.

• Одно из наиболее важных распределений в статистике — нормальное распределение (normal distribution), которое иногда называют гауссовым(Gaussian distribution). • Можно вычислить вероятность того, что нормально распределенная случайная величина лежит в заданном интервале. • Однако вероятность того, что она принимает наперед заданное значение, равна нулю. • Это отличает непрерывные случайные величины (измеряемые) от дискретных (подсчитываемых). • Например, время измеряется, а не подсчитывается. Следовательно, можно вычислить вероятность того, что Web страница будет загружаться от 7 до 10 с. Сужая заданный интервал, можно вычислить вероятность того, что она будет загружаться от 8 до 9 с. Кроме того, можно вычислить вероятность того, что она будет загружаться от 8, 99 до 9, 01 с. Однако вероятность того, что Web страница будет загружаться ровно 8 с, равна нулю.

Нормальное распределение • Распределение количественных данных, таких как размеры, масса, влажность и т. д. , собранных за определенный период (например за месяц) при достаточном числе наблюдений (порядка 100), представленных графически гистограммой, близко к нормальному (гауссову) распределению.

Важность нормального распределения в статистике обусловлена тремя причинами • Оно описывает (точно или приблизительно) распределение многих непрерывных случайных величин. • С помощью нормального распределения можно аппроксимировать разнообразные дискретные распределения • Нормальное распределение тесно связано с центральной предельной теоремой (central limit theorem)

Центральная предельная теорема • При достаточно большом объеме выборок выборочное распределение средних можно апроксимировать нормальным распределением. Это свойство не зависит от вида распределения генеральной совокупности. • Какой объем выборки следует считать достаточно большим? • Для подавляющего большинства совокупностей выборочное распределение средних становится приблизительно нормальным при n = 30

Контрольный листок для анализа стабильности процесса

• Сумма независимых случайных величин асимптотически стремится к нормальному распределению. • Пусть Х 1, Х 2, . . . Хn — независимые одинаково распределенные случайные величины. Тогда при увеличении п закон распределения суммы этих величин неограниченно приближается к нормальному. • Вопрос о том, при каких значениях п распределение можно приближенно считать нормальным, зависит от точности расчетов.

• Нормальным распределением (или законом Гаусса) называется распределение непрерывной случайной величины, плотность которой определяется по формуле • Где m и σ параметры распределения • Для краткой записи нормального распределения с параметрами т и σ используют обозначение N (m, σ) Можно доказать, что параметр m равен математическому ожиданию, а параметр σ стандартному отклонению случайной величины X.

• К сожалению, вычислить математическое выражение, заданное формулой довольно сложно. • Чтобы упростить задачу, значения плотности нормального распределения, как правило, табулируют. • Поскольку количество возможных комбинаций параметров m и σ бесконечно, для вычислений понадобилось бы бесконечное количество таблиц. • Однако, если нормировать (standardize) данные, все распределения можно свести к одной таблице. • Используя формулу преобразования (transformation formula), любую нормально распределенную случайную величину X можно преобразовать в нормированную нормально распределенную случайную величину Z

• В частном случае параметр m = 0, σ = 1. • Нормальное распределение N(0, 1) называется стандартным нормальным распределением. • В этом случае плотность распределения Кривая распределения, построенная по формуле, имеет колообразный вид, вертикальная ось является осью симметрии, горизонтальная — асимптотой. Максимальное значение ординаты равно

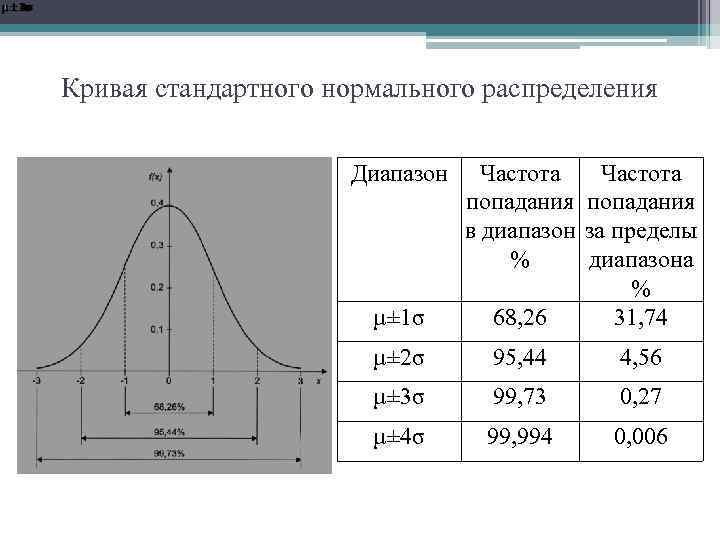Кривая стандартного нормального распределения Диапазон µ± 1σ Частота попадания в диапазон за пределы % диапазона % 68, 26 31, 74 µ± 2σ 95, 44 4, 56 µ± 3σ 99, 73 0, 27 µ± 4σ 99, 994 0, 006

• Как можно видеть, вероятность того, что данные выйдут за предел диапазона тройного стандартного отклонения, составляет 0, 27%, т. е. примерно 0, 3%. • Это значит, что в случае, когда стандартное значение параметра изделия отличается от среднего значения на 3σ, если даже все изделия сделанной из партии выборки при выборочной проверке оказались годными, в партии около 0, 3% изделий могут оказаться бракованными.

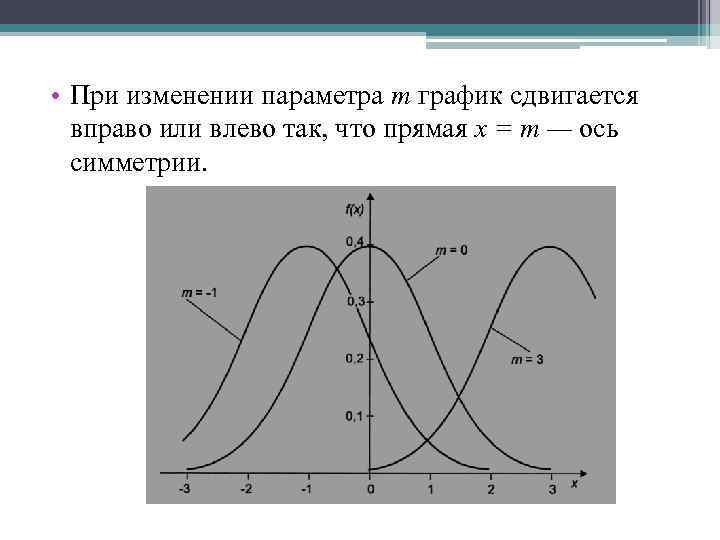• При изменении параметра т график сдвигается вправо или влево так, что прямая х = т — ось симметрии.

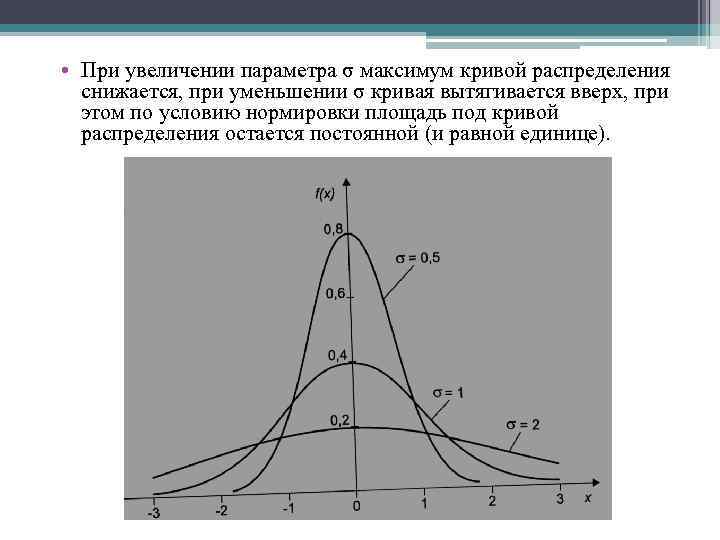• При увеличении параметра σ максимум кривой распределения снижается, при уменьшении σ кривая вытягивается вверх, при этом по условию нормировки площадь под кривой распределения остается постоянной (и равной единице).

СВОЙСТВА НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ • Имеет колообразную (а значит, симметричную) форму • Его математическое ожидание, медиана и мода совпадают друг с другом • Основная масса нормально распределенных значений лежит в интервале, длина которого равна 4/3 стандартного отклонения. • Значения нормально распределенной случайной величины лежат на всей числовой оси ( ∞ < X < +∞ )

• Медиана – число, разделяющее выборку пополам: 50% элементов меньше медианы, 50% элементов – больше. • Мода – число, которое чаще других встречается в выборке.

Функция Лапласа • Стандартное нормальное распределение N(0, 1) называют функцией Лапласа (функция распределения нормально распределенной случайной величины). • Она имеет специальное обозначение Эта функция табулирована, например Например, Ф (2, 48) = 0, 9934. Из симметрии графика функции вытекает соотношение Ф(-х) = 1 Ф(х).

Г рафик функции Лапласа

• Можно установить связь между функцией распределения F(x)для распределения N(m, σ) и функцией стандартного нормального распределения: Вероятность попадания нормально распределенной случайной величины в интервал от х1 до х2 определяется по формуле

• Часто в расчетах надо найти вероятность того, что случайная величина X не слишком сильно отклонится от своего математического ожидания т Пусть, например, е = 3σ. Используя таблицы функции стандартного нормального распределения, найдем: поэтому вероятность того, что случайная величина отклонится от математического ожидания больше, чем на 3σ, ничтожно мала:

Пример • На станке автомате изготавливаются валики номинальным диаметром 10 мм. Стандартное отклонение, характеризующее точность станка, составляет σ = 0, 03 мм. Сколько в среднем валиков из ста удовлетворяют стандарту, если для этого требуется, чтобы диаметр отклонялся от номинального не более чем на 0, 05 мм? т. е. примерно 90 валиков из каждых 100 удовлетворяют стандарту.

АППРОКСИМАЦИЯ БИНОМИАЛЬНОГО И ПУАССОНОВСКОГО РАСПРЕДЕЛЕНИЙ С ПОМОЩЬЮ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

• При систематизации количественных данных, полученных в результате контроля, можно видеть, что число дефектных изделий рп и доля дефектных изделий р подчиняются биномиальному распределению. • Суммарное число дефектов С подчиняется закону распределения Пуассона. • Оба эти распределения не обладают двусторонней симметрией, а вытянуты вправо от оси ординат. Однако если число дефектных изделий рп и среднее число дефектов на единицу площади λ велики (pn 5; λ 5), и то и другое распределение приближается к нормальному, поэтому в расчетах можно использовать нормальное распределение.

Поправка на непрерывность распределения • ДСВ может принимать лишь фиксированные значения, в то время как НСВ может принимать любые значения на числовой прямой или в интервале. Следовательно, ис пользуя нормальное распределение для аппроксимации биномиального или пуассоновского распределения, для того чтобы достичь хорошего приближения, мы должны де лать поправку на непрерывность. • Вероятность того, что непрерывно распределенная случайная величина (в том числе, имеющая нормальное распределение) принимает конкретное значение, равна нулю. Когда нормальное распределение применяется для аппроксима ции биномиального, поправка на непрерывность позволяет приближенно вычислить вероятность того, что дискретная случайная величина принимает конкретное значение.

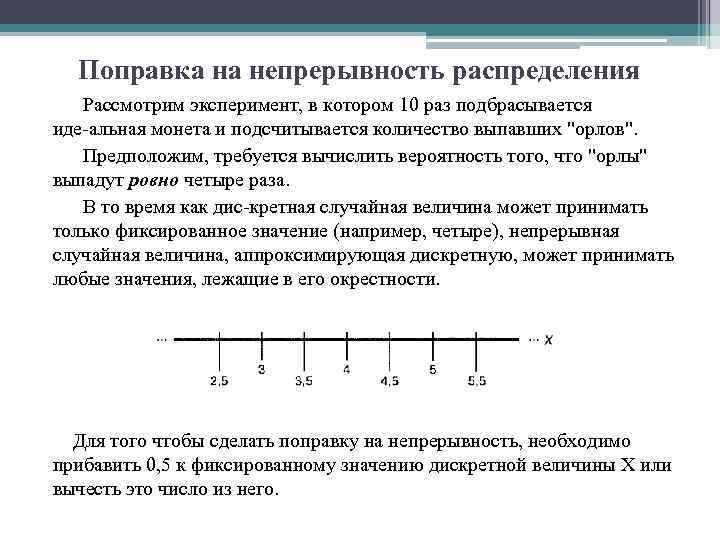Поправка на непрерывность распределения Рассмотрим эксперимент, в котором 10 раз подбрасывается иде альная монета и подсчитывается количество выпавших "орлов". Предположим, требуется вычислить вероятность того, что "орлы" выпадут ровно четыре раза. В то время как дис кретная случайная величина может принимать только фиксированное значение (например, четыре), непрерывная случайная величина, аппроксимирующая дискретную, может принимать любые значения, лежащие в его окрестности. Для того чтобы сделать поправку на непрерывность, необходимо прибавить 0, 5 к фиксированному значению дискретной величины X или вычесть это число из него.

Поправка на непрерывность распределения • Чтобы аппроксимировать вероятность того, что "орел" выпадет ровно четыре раза (т. е. X = 4), необходимо вычислить площадь фигуры, лежащей под кривой нормального распределения между значениями Х= 3, 5 и Х = 4, 5. • Чтобы вычислить вероятность того, что орлы выпадут не менее четырех раз, нужно определить площадь фигуры, лежащей под нормальной кривой справа от точки X = 3, 5, поскольку число 3, 5 является в данном случае нижней границей непрерывной случайной величи ны . X • Чтобы вычислить вероятность того, что орлы выпадут не более четырех раз, следует определить площадь фигуры, лежащей под нормальной кри вой слева от точки = 4, 5, поскольку число 4, 5 в X данном случае является верхней гра ницей непрерывной случайной величины X. • При аппроксимации дискретных распределений с помощью нормального точное употребление слов играет очень важную роль.

Поправка на непрерывность распределения • Для того чтобы приближенно вычислить вероятность того, что при десятикратном подбрасывании монеты выпадет меньше че тырех орлов, необходимо определить площадь фигуры, лежащей под нормальной кри вой слева от точки = 3, 5. X • Для того чтобы приближенно вычислить вероятность того, что при десятикратном подбрасывании монеты выпадет больше четырех орлов, необхо димо определить площадь фигуры, лежащей под нормальной кривой справа от точки Х = 4, 5. • Для того чтобы приближенно вычислить вероятность того, что при десяти кратном подбрасывании монеты выпадет т 4 до 7 о орлов, необходимо определить пло щадь фигуры, лежащей под нормальной кривой между точками X = 3, 5 и Х = 7, 5.

Аппроксимация биномиального распределения • Биномиальное распределение является симметричным (как и нормальное), если р = 0, 5. • Если р ≠ 0, 5, биномиальное распределение становится несим метричным. • Однако, чем ближе параметр р к числу 0, 5 и чем больше количество выбороч ных наблюдений , тем более симметричным становится п биномиальное распределение. • По мере увеличения объема выборки процесс вычисления точных вероятностей успеха по формуле биноминального распределения становится все более сложным. • При увеличении объема выборки для аппроксимации точных вероятностей успеха можно использовать нормальное распределение. • Как правило, нормальное распределение можно применять, когда числа пр и п(1 -р) больше пяти.

Аппроксимация биномиального распределения • Математическое ожидание биномиального распределения равно • а стандартное отклонение • Подставив эти величины в формулу преобразования • получим • Следовательно, при достаточно больших значениях п случайная величина Z будет иметь приближенное нормальное распределение.

Аппроксимация биномиального распределения •

Аппроксимация биномиального распределения ПРИМЕР • Предположим, что из крупной партии шин, содержащей 8% бракованной продук ции, случайным образом выбраны = 1 600 шин одинакового п типа. Какова вероят ность того, что в этой выборке обнаружатся не более 150 дефектных шин? • РЕШЕНИЕ. Поскольку пр = 1 600 х 0, 08 = 128 и п(1 -р) = 1600 х 0, 92 = 1472 больше пяти, для аппроксимации биномиального распределения можно применять нор мальное распределение. Здесь число Ха = 150, 5 является скорректированным количеством успехов, а вели чина = +2, 07. Используя таблицу, находим, что площадь фигуры, Z лежащей под нормальной кри вой слева от точки = +2, 07, равна 0, 9808 Z

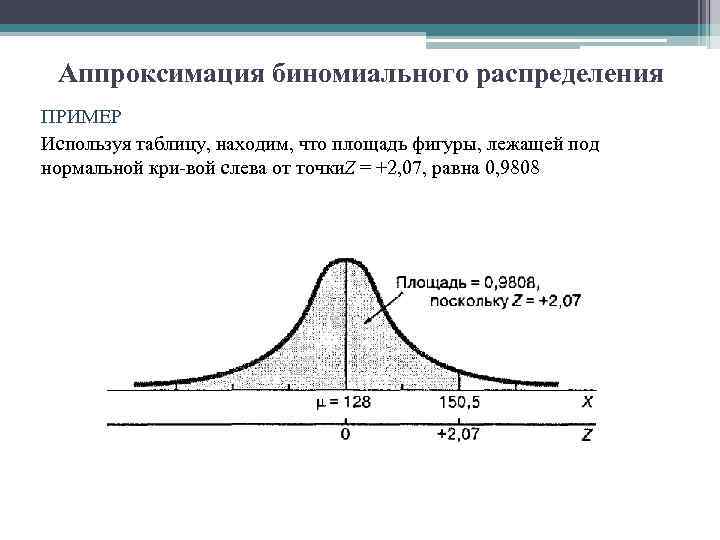Аппроксимация биномиального распределения ПРИМЕР Используя таблицу, находим, что площадь фигуры, лежащей под нормальной кри вой слева от точки = +2, 07, равна 0, 9808 Z

Аппроксимация биномиального распределения ПРИМЕР Если бы мы применили биномиальное распределение, то вычислить вероятность то го, что выборка содержит не более 150 дефектных шин, было бы трудно. Применение нормального распределения вместо биномиального экономит время на расчеты. Для решения задачи, используя формулу биноминального распределения, необходимо вычислить 151 слагаемых:

Аппроксимация биномиального распределения ПРИМЕР Вычисление приближенной вероятности по конкретному значению. Предполо жим , требуется вычислить вероятность того, что в выборке будет обнаружено ровно 150 бракованных шин. Поправка на непрерывность означает, что вероятность обнару жить 150 бракованных шин равна площади фигуры, лежащей под нормальной кривой между точками 149, 5 и 150, 5. Следовательно, получаем В таблице находим, что площадь фигуры, лежащей под нормальной кривой слева от точки Х= 150, 5 (Z = +2, 07), равна 0, 9808, а площадь фигуры, лежащей под нор мальной кривой слева от точки = 149, 5 (Z = +l, 98), равна Х 0, 9761. Следовательно, приближенная вероятность того, что выборка содержит 150 бракованных шин, равна разности между этими двумя площадями, т. е. числу 0, 0047

Аппроксимация распределения Пуассона • Пуассоновское распределение можно аппроксимировать нормальным, если пара метр — ожидаемое количество успехов — больше или λ равно пяти. Поскольку матема тическое ожидание и дисперсия распределения Пуассона совпадают • стандартное отклонение равно • Подставляя эти величины в формулу преобразования, получаем • Следовательно, при достаточно больших значениях λ случайная величина Z будет иметь приближенно нормальное распределение.

Аппроксимация распределения Пуассона •

Аппроксимация распределения Пуассона ПРИМЕР Предположим, что на некоем автомобильном заводе среднее количество остановок работы вследствие проблем с оборудованием равно 12, 0. Чему равна приближенная вероятность того, что в указанный день будет не более 15 остановок работы из за про блем с оборудованием? Используя формулу, получаем Здесь Ха — скорректированное количество успехов, равное 15, 5. Следовательно, прибли женная вероятность того, что величина не X превосходит заданное значение, равна веро ятности того, что случайная величина. Z не превосходит +1, 01. В таблице находим, что площадь фигуры, лежащей под нормальной кривой слева от точки Z = +l, 01, равна 0, 8438. Следовательно, приближенная вероятность того, что в указанный день будет не более 15 остановок работы из за проблем с оборудованием, равно 0, 8438. Эта величина хо рошо согласуется с истинной пуассоновской вероятностью, равной 0, 8445.

ВЫБОРКИ ИЗ КОНЕЧНЫХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ • Центральная предельная теорема, а также формулы для вычисления стандартной ошибки среднего и стандартной ошибки доли признака основаны на предположении, что выборки извлекаются из генеральной совокупности с возвращением. • Однако прак тически во всех статистических исследованиях выборки извлекаются из генеральных совокупностей конечного объема N без возвращения. • Если объем выборок п достаточно велик по сравнению с объемом генеральной совокупности N (т. е. выборка содержит бо лее 5% элементов генеральной совокупности), так что n/N > 0, 05, то при вычислении стандартной ошибки среднего и стандартной ошибки доли признака следует учитывать поправочный коэффициент для конечной генеральной совокупности. Эта поправка вычисляется по формуле. • где п — объем выборки, а N — объем генеральной совокупности.

ВЫБОРКИ ИЗ КОНЕЧНЫХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ • формулы для вычисления стандартной ошибки среднего и стан дартной ошибки доли признака принимают следующий ид в • Анализ формулы для вычисления поправочного коэффициента для конечной гене ральной совокупности оказывает, что ее числитель п всегда меньше знаменателя, поскольку число п всегда больше единицы. Следовательно, поправочный коэффициент для конечной генеральной совокупности меньше единицы. Поскольку этот коэффици ент умножается на стандартную ошибку, скорректированная стандартная ошибка уменьшается. Таким образом, с учетом поправочного коэффициента для конечной гене ральной совокупности мы получаем более точные оценки.

ВЫБОРКИ ИЗ КОНЕЧНЫХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ • Из генеральной совокупности упаковок извлекалась выборка, состоящая из 25 коробок. Допустим, что за день фабрика заполняет 2000 коробок, которые образуют всю генеральную совокупность. Используя поправочный коэффициент для конечной генеральной совокупности, опреде лите вероятность извлечь выборку, среднее выборочное которой меньше 365 г. • Используя формулу при σ = 15, n = 25 и N = 2000, получаем • Вероятность извлечь выборку, выборочное среднее которой лежит между 365 и 368 г, вычисляется следующим образом

ВЫБОРКИ ИЗ КОНЕЧНЫХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ • Из таблицы следует, что площадь области, ограниченной нормальной кривой и соответствующей весу коробки, не превышающему 365 г, равна 0, 1562. • Очевидно, что в данном примере учет поправочного коэффициента для конечной генеральной совокупности очень мало влияет на стандартную ошибку среднего и площадь области, ограниченной нормальной кривой, поскольку объем выборки (т. е. , n = 25) составляет только 1, 25% от всей генеральной совокупности (т. е. , N = 2000).

Равномерное распределение Случайная величина имеет равномерное распределение, если вероятность того, что она принимает любое значение в интервале, ограниченном минимальным числом а и максимальным числом Ь, постоянна. Поскольку график плотности этого распределения имеет вид прямоугольника, равномерное распределение иногда называют прямоугольным Плотность равномерного распределения:

• Математическое ожидание равномерного распределения • Дисперсия равномерного распределения • Стандартное отклонение равномерного распределения

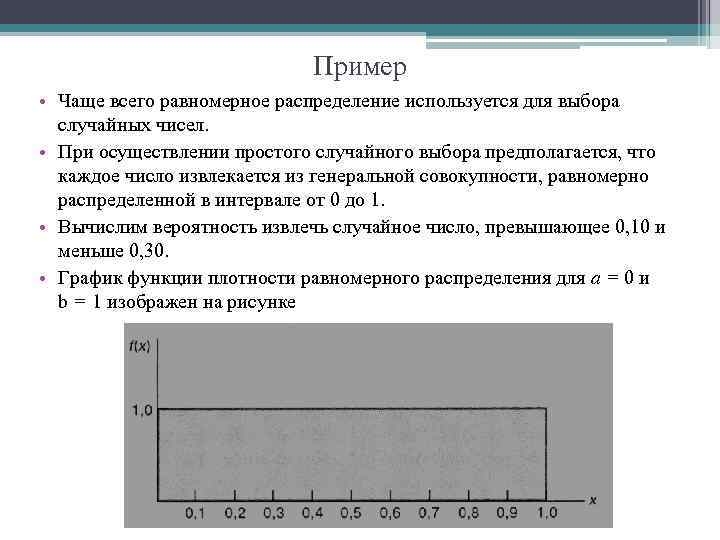Пример • Чаще всего равномерное распределение используется для выбора случайных чисел. • При осуществлении простого случайного выбора предполагается, что каждое число извлекается из генеральной совокупности, равномерно распределенной в интервале от 0 до 1. • Вычислим вероятность извлечь случайное число, превышающее 0, 10 и меньше 0, 30. • График функции плотности равномерного распределения для а = 0 и b = 1 изображен на рисунке

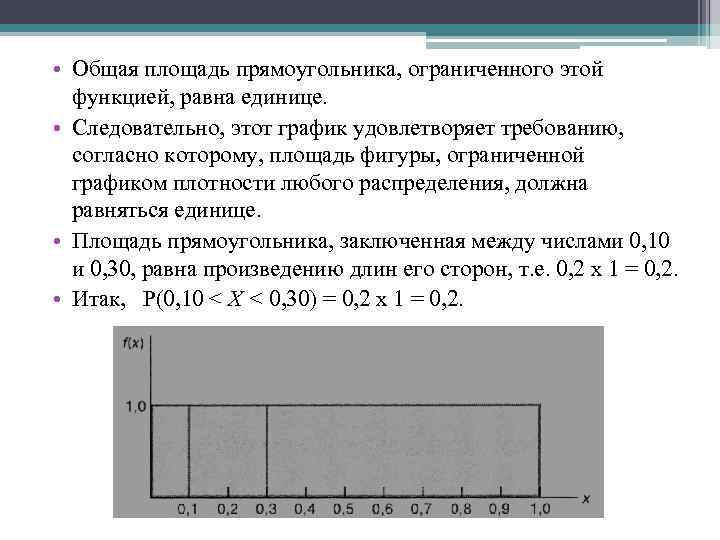• Общая площадь прямоугольника, ограниченного этой функцией, равна единице. • Следовательно, этот график удовлетворяет требованию, согласно которому, площадь фигуры, ограниченной графиком плотности любого распределения, должна равняться единице. • Площадь прямоугольника, заключенная между числами 0, 10 и 0, 30, равна произведению длин его сторон, т. е. 0, 2 х 1 = 0, 2. • Итак, Р(0, 10 < X < 0, 30) = 0, 2 х 1 = 0, 2.

• Математическое ожидание, дисперсия и стандартное отклонение равномерного распределения при а = 0 и b = 1 вычисляются следующим образом.

Экспоненциальное распределение (показательное) • Экспоненциальное распределение оказывается весьма полезным при моделировании производства и систем массового обслуживания. Оно широко используется в теории расписаний (очередей) для моделирования промежутков времени между двумя запросами, которые могут представлять собой поступление пациента в больницу, а также посещение Web сайта.

• Экспоненциальное распределение зависит только от одного параметра который обозначается буквой λ и представляет собой среднее количество запросов, поступающих в систему за единицу времени. • Величина 1/λ равна среднему промежутку времени, прошедшего между двумя последовательными запросами.

• Плотность распределения • Математическое ожидание • Дисперсия

• Например, если в систему в среднем поступает 4 запроса в минуту, т. е. λ = 4, то среднее время, прошедшее между двумя последовательными запросами, равно 1/λ = 0, 25 мин. , или 15 с. Вероятность то го, что следующий запрос поступит раньше, чем через X единиц времени, определяется по формуле

• Проиллюстрируем применение экспоненциального распределения следующим примером. • Допустим, что в отделение банка приходят 20 клиентов в час. • Предположим, что в банк уже пришел один клиент. • Какова вероятность того, что следующий клиент придет в течение 6 мин. (т. е. 0, 1 ч)? • В данном случае λ = 20, а X = 0, 1. Используя формулу, получаем: Таким образом, вероятность, что следующий клиент придет в течение 6 мин. , равна 0, 8647, т. е. 86, 47%.

Спасибо за внимание

• Медиана. Медианой называется число, разделяющее выборку пополам: 50% элементов больше медианы, 50% меньше • Мода это число, которое чаще других встречается в выборке. • Квантиль – это показатели, которые используют для оценки распределения данных при описании свойств больших числовых выборок. Квантили разбивают упорядоченный набор данных на части. • Квантилью порядка р называется число z , для которого функция распределения F(x) принимает значение р

• Первый квантиль – это число, разделяющее выборку на две части: 25% элементов меньше, а 75% элементов больше первого квантиля. • Q 1=(n+1)/4 – й элемент упорядоченного массива • Третий квантиль это число, разделяющее выборку на две части: 75% элементов меньше, а 25% элементов больше первого квантиля. • Q 3=3(n+1)/4 – й элемент упорядоченного массива

Число степеней свободы Шиндовский, Э. Статистические методы управления качеством •

Число степеней свободы • Знаменатель n 1 представляет собой «степень свободы» , т. е. число независимых величин из • Только n 1 величин являются независимыми, так как должно выполняться равенство • Итак, число степеней свободы определяется объемом выборки (число независимых наблюдений), уменьшенной на число параметров, оцениваемых по этой выборке. • Если дисперсия вычисляется с небольшим числом степеней свободы, то она колеблется в сравнительно широких пределах, что можно приписать влиянию случайных факторов. • Если вычисление дисперсии производится с большим числом степеней свободы, то колебания становятся меньше.

Распределение хи-квадрат • Пусть Xi - случайные величины, имеющие стандартное нормальное распределение N (0, 1). Распределение суммы квадратов этих величин • называется распределением хи-квадрат с к степенями свободы

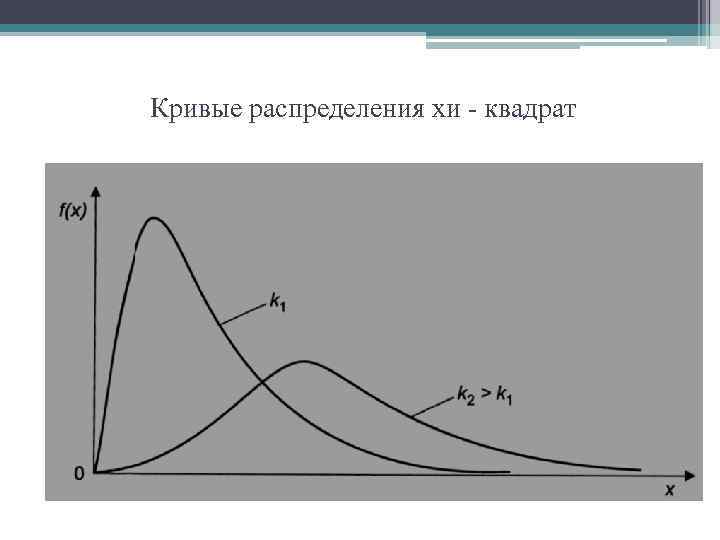Кривые распределения хи квадрат

Распределение Стьюдента • Распределением Стьюдента (или tраспределением) называется распределение случайной величины: • где Z – случайная величина, распределенная по стандартному нормальному закону. независимая от Z случайная величина, имеющая – «ХИ квадрат» распределение с k степенями свободы.

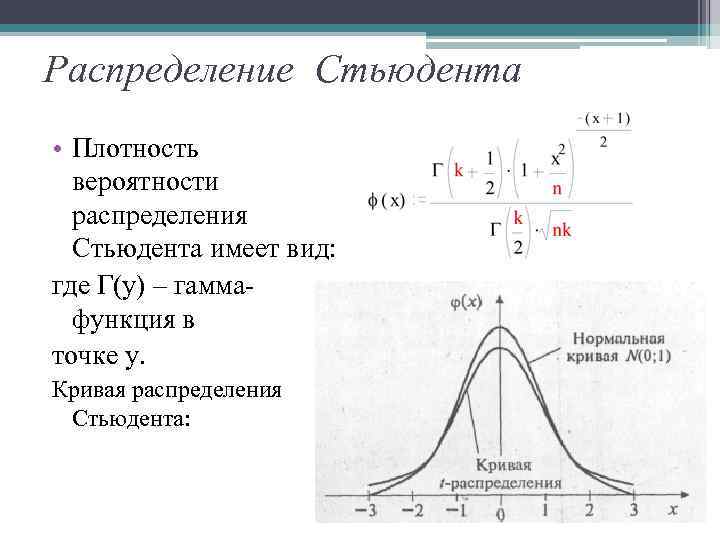Распределение Стьюдента • Плотность вероятности распределения Стьюдента имеет вид: где Г(y) – гамма функция в точке y. Кривая распределения Стьюдента:

Распределение Фишера-Снедекора • Распределением Фишера-Снедекора (или Fраспределением) называется распределение случайной величины: где Г(y) – гамма функция Эйлера в точке y.

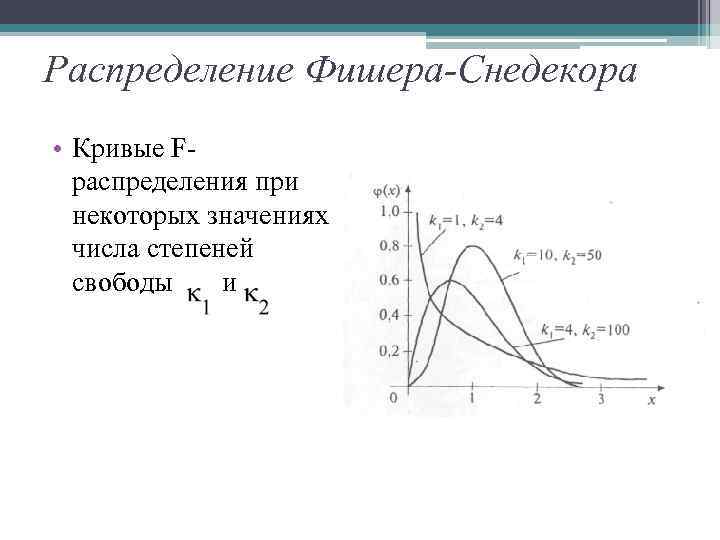Распределение Фишера-Снедекора • Кривые F распределения при некоторых значениях числа степеней свободы и