Теоретические основы компьютера l l l Представление чисел

Теоретические основы компьютера l l l Представление чисел Машинная арифметика Представление команд

Системы счисления. Перевод десятичных чисел из одной системы счисления в другую и обратно v Системы счисления. Виды систем счисления. v Перевод десятичных чисел из десятичной системы счисления в любую другую и обратно. v Перевод целых чисел из десятичной системы счисления с помощью приложения Калькулятор в двоичную, восьмеричную, шестнадцатеричную системы счисления. v Перевод целых чисел из десятичной системы счисления с помощью приложения Excel в двоичную, восьмеричную, шестнадцатеричную системы счисления, используя общий метод перевода.

Основные понятия темы Цифра - это символ, используемый в записи числа. 12 двенадцать ХII - различные способы записи одного числа - значение числа остается неизменным Система счисления - это способ записи (изображения) чисел. Алфавит системы счисления - это множество всех символов (знаков), используемых для записи чисел в данной системе счисления. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - алфавит десятичной позиционной системы счисления I, V, X, L, C, D, M - алфавит римской непозиционной системы счисления

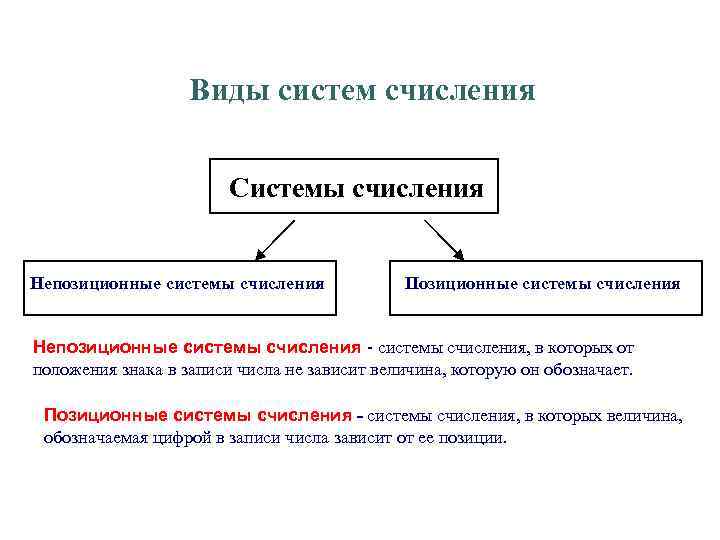Виды систем счисления Системы счисления Непозиционные системы счисления Позиционные системы счисления Непозиционные системы счисления - системы счисления, в которых от положения знака в записи числа не зависит величина, которую он обозначает. Позиционные системы счисления - системы счисления, в которых величина, обозначаемая цифрой в записи числа зависит от ее позиции.

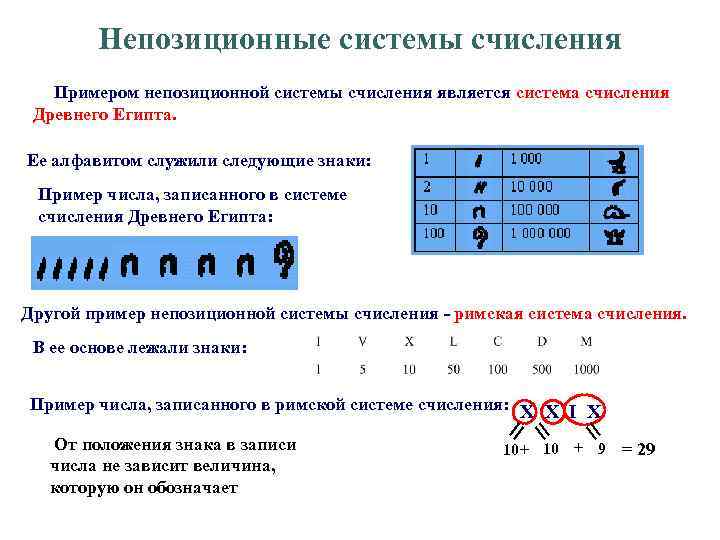Непозиционные системы счисления Примером непозиционной системы счисления является система счисления Древнего Египта. Ее алфавитом служили следующие знаки: Пример числа, записанного в системе счисления Древнего Египта: Другой пример непозиционной системы счисления - римская система счисления. В ее основе лежали знаки: Пример числа, записанного в римской системе счисления: X X I Х От положения знака в записи числа не зависит величина, которую он обозначает 10 + 9 = 29

Число в позиционной системе счисления Привычная нам десятичная система является позиционной системой счисления: Цифры 5, находящиеся на разных позициях, имеют различные количественные значения. 155255 = 1 · 105 + 5 · 104 + 5 · 103 + 2 · 102 + 5 · 101 + 5 · 100 сотни десятки единицы тысячи десятки тысяч сотни тысяч Основание позиционной системы счисления - целое число, которое возводится в степень. 10 - основание десятичной позиционной системы счисления. Базис позиционной системы счисления - последовательность чисел, каждое из которых определяет количественный эквивалент (вес) символа в зависимости от его места в записи числа. 101, 102, 103, 104, … , 10 n, … - базис десятичной позиционной системы счисления.

Представление числа в системе счисления 155255 = 1 · 105 + 5 · 104 + 5 · 103 + 2 · 102 + 5 · 101 + 5 · 100 2534, 65 = 2 · 103 + 5 · 102 + 3 · 101 + 4 · 100 + 6 · 10 -1 + 5 · 10 -2 Формула представления числа Хb = an · bп + … + a 0 · b 0 + a-1 · b-1 +. . . Пример представления числа в 10 -тичной системе счисления: 6110 = 6 · 101 + 1 · 100 3420, 57610 = 3 · 103 + 4 · 102 + 2 · 101 + 0 · 100 + + 5 · 10 -1 + 7 · 10 -2 + 6 · 10 -3 Пример представления числа в 2 -ичной системе счисления: 1111012 = 1 · 25 + 1 · 24 + 1 · 23 + 1 · 22 + 0 · 21 + 1 · 20 = 32 + 16 + 8 + 4 + 1 = 6110 111, 0112= 1 · 22 + 1 · 21 + 1 · 20 + 0 · 2 -1 + + 1 · 2 -2 + 1 · 2 -3 Пример представления числа в 16 -ричной системе счисления: 3 D 16 = 3 · 161 + 13 · 160 A 32 D, 2 E 16 = 10 · 163 + 3 · 162 + 2 · 161 + 13 · 160 + + 2 · 16 -1 + 14 · 16 -2

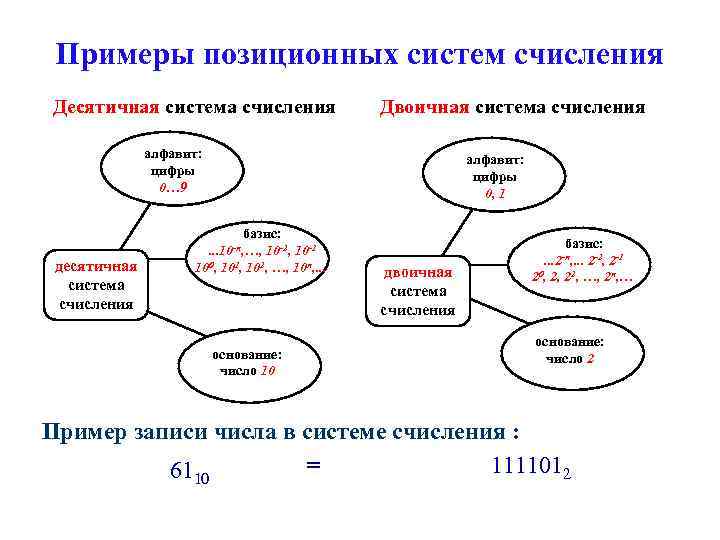Примеры позиционных систем счисления Десятичная система счисления Двоичная система счисления алфавит: цифры 0… 9 десятичная система счисления алфавит: цифры 0, 1 базис: 10 -2, 10 -1 100, 101, 102, …, 10 п, . . . 10 -п, …, основание: число 10 двоичная система счисления базис: . . . 2 -п, . . . 2 -2, 2 -1 20, 2, 22, …, 2 п, … основание: число 2 Пример записи числа в системе счисления : = 1111012 6110

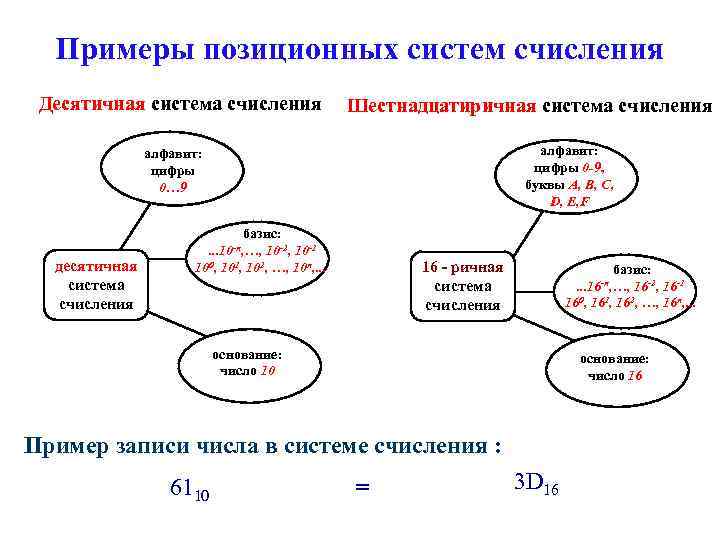Примеры позиционных систем счисления Десятичная система счисления Шестнадцатиричная система счисления алфавит: цифры 0 -9, буквы A, B, C, D, E, F алфавит: цифры 0… 9 десятичная система счисления базис: 10 -2, 10 -1 100, 101, 102, …, 10 п, . . . 10 -п, …, 16 - ричная система счисления базис: 16 -2, 16 -1 160, 161, 162, …, 16 п, . . . 16 -п, …, основание: число 10 основание: число 16 Пример записи числа в системе счисления : 6110 = 3 D 16

Перевод десятичного числа 2359, 407 в двоичное Нахождение целой части числа (деление на 2) Нахождение дробной части числа (умножение на 2) 407 2 814 2 628 2 256 2 512 2 024 2 048 2 096 1 1 1 0 0 1 Целая часть : 1 0 0 1 1 1 Порядок записи целых чисел 2359 1179 589 294 147 73 36 18 9 4 2 1 Порядок записи остатков 0 1 1 0 0 Дробная часть : 0 1 1 0 0 2359, 407 = 1 0 0 1 1 1, 0 1 1 0 02

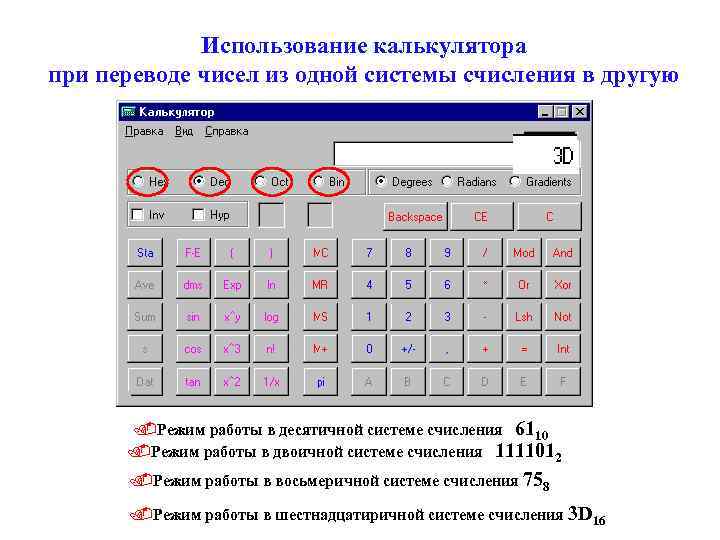Использование калькулятора при переводе чисел из одной системы счисления в другую . Режим работы в десятичной системе счисления 6110. Режим работы в двоичной системе счисления 1111012. Режим работы в восьмеричной системе счисления 758. Режим работы в шестнадцатиричной системе счисления 3 D 16

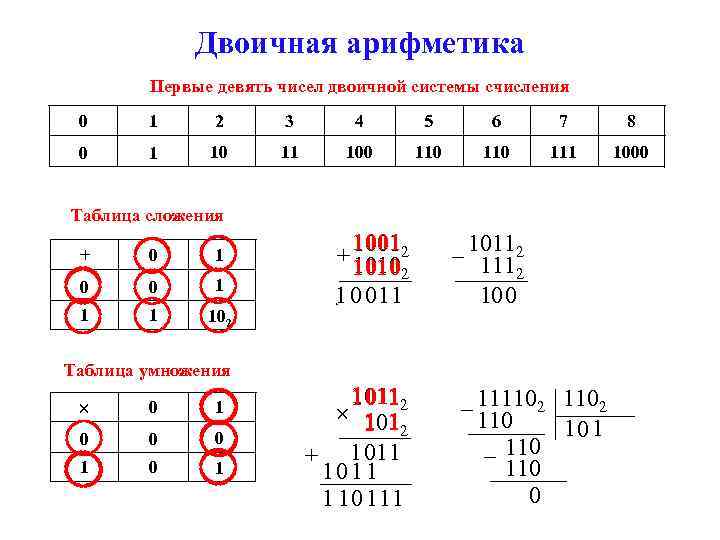Двоичная арифметика Первые девять чисел двоичной системы счисления 0 1 2 3 4 5 6 7 8 0 1 10 11 100 110 111 1000 Таблица сложения + 0 1 0 0 1 102 1 001 1001 + 1 0102 1010 2 1 0 01 1 1011 – 1112 2 10 0 1 Таблица умножения 0 1 0 0 0 1 1 0112 1011 1 1 1012 + 1 011 1 10 1 11 – 111102 110 10 1 – 110 0

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную Алгоритмы, описанные ниже, могут применяться при переводе чисел между системами счисления, основания которых являются степенями числа 2. Такие алгоритмы могут применяться для перевода чисел между двоичной, восьмеричной и шестнадцатеричной системами счисления. Для записи двоичных чисел используются две цифры, т. е. в каждом разряде числа возможны два варианта записи. Каждый разряд двоичного числа содержит 1 бит. Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны восемь вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита. Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. в каждом разряде числа возможны шестнадцать вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита.

Для перевода дробного двоичного числа в восьмеричное нужно: v. Запись числа разбить слева направо на триады (если в последней правой группе окажется меньше, чем три разряда, то необходимо её дополнить справа нулями) v. Преобразовать каждую триаду в восьмеричную цифру Переведём таким образом двоичное число 0, 1101012 в восьмеричное: Двоичные триады Восьмеричные цифры Получаем 0, 1101012 = 0, 658 101 110 5 6

Для перевода целого двоичного числа в шестнадцатеричное нужно: v. Разбить его на группы по четыре цифры (тетрады), справа налево (если в последней левой группе окажется меньше, чем четыре разряда, то необходимо её дополнить слева нулями) v. Преобразовать каждую группу в шестнадцатеричную цифру Переведём таким образом двоичное число 1010012 в шестнадцатеричное: Двоичные тетрады Шестнадцатеричные цифры Получаем 1010012 = 2916 0010 1001 2 9

Для перевода дробного двоичного числа в шестнадцатеричное нужно: v. Разбить его на тетрады, слева направо (если в последней правой группе окажется меньше, чем четыре разряда, то необходимо её дополнить справа нулями) v. Преобразовать каждую группу в шестнадцатеричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия двоичных тетрад и шестнадцатеричных цифр Переведём таким образом дробное двоичное число 0, 1101012 в шестнадцатеричную систему счисления: Двоичные тетрады 1101 0100 Шестнадцатеричные цифры D (14) 4 Получаем 0, 1101012 = 0, D 416

Перевод чисел из восьмеричной и шестнадцатеричной систем в двоичную: vдля перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в триаду vдля перевода из шестнадцатеричной системы в двоичную каждую цифру числа надо преобразовать в тетраду Переведём дробное восьмеричное число 0, 478 в двоичную систему счисления: Восьмеричные цифры 4 7 Двоичные триады 100 111 Получаем 0, 478 = 0, 1001112 Переведём целое шестнадцатеричное число АВ 1616 в двоичную систему счисления: Шестнадцатеричные цифры Двоичные тетрады Получаем АВ 1616 = 101010112 А В 1010 1011

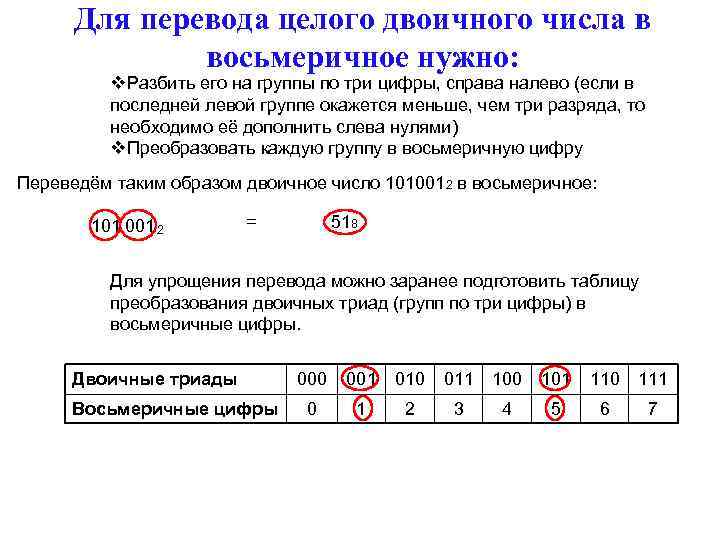Для перевода целого двоичного числа в восьмеричное нужно: v. Разбить его на группы по три цифры, справа налево (если в последней левой группе окажется меньше, чем три разряда, то необходимо её дополнить слева нулями) v. Преобразовать каждую группу в восьмеричную цифру Переведём таким образом двоичное число 1010012 в восьмеричное: 101 001 2 = 518 Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по три цифры) в восьмеричные цифры. Двоичные триады Восьмеричные цифры 000 001 010 011 100 101 110 111 0 1 2 3 4 5 6 7

Использование калькулятора при переводе чисел из одной системы счисления в другую ПРИМЕР Перевести число 2359 из десятичной системы счисления в шестнадцатиричную при помощи калькулятора . Выбираем режим работы в той системе, в которой дано число ( десятичная система); . Набираем число, с которым хотим работать (2359); . Переключаемся в режим работы системы счисления, в которой требуется получить ответ (шестнадцатиричная система) и получаем результат.