 Теоретическая информатика Щелкунов Д. А.
Теоретическая информатика Щелкунов Д. А.
 Теоретическая информатика • Теоретическая информатика — это научная область, предметом изучения которой являются информация и информационные процессы, в которой осуществляется изобретение и создание новых средств работы с информацией. • Теоретическая информатика — математическая дисциплина использующая методы математики для построения и изучения моделей обработки, передачи и использования информации.
Теоретическая информатика • Теоретическая информатика — это научная область, предметом изучения которой являются информация и информационные процессы, в которой осуществляется изобретение и создание новых средств работы с информацией. • Теоретическая информатика — математическая дисциплина использующая методы математики для построения и изучения моделей обработки, передачи и использования информации.
 Информация • Информация есть информация, а не материя или энергия (Норберт Виннер). • Синтаксис определяет все допустимые символы или их последовтельности. • Семантика объясняет их значения. • Прагматика объясняет истинный смысл и область применения. • Синтаксис + Семантика -> Данные • Данные + Прагматика -> Сообщение (известия, руководство к действию)
Информация • Информация есть информация, а не материя или энергия (Норберт Виннер). • Синтаксис определяет все допустимые символы или их последовтельности. • Семантика объясняет их значения. • Прагматика объясняет истинный смысл и область применения. • Синтаксис + Семантика -> Данные • Данные + Прагматика -> Сообщение (известия, руководство к действию)
 Информация Удвоение информации
Информация Удвоение информации
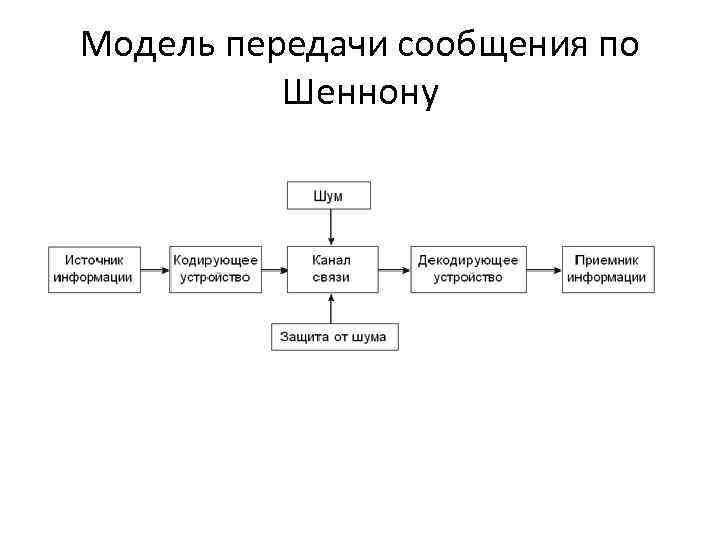 Модель передачи сообщения по Шеннону
Модель передачи сообщения по Шеннону
 Системы счисления • Система счисления - символический метод записи чисел, представление чисел с помощью письменных знаков. • Позиционная система счисления – система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).
Системы счисления • Система счисления - символический метод записи чисел, представление чисел с помощью письменных знаков. • Позиционная система счисления – система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).
 Системы счисления
Системы счисления
 Системы счисления. Перевод из двоичной
Системы счисления. Перевод из двоичной
 Биты и байты • Бит – единица хранения цифровой информации, принимающая одно из двух значений {0, 1}. • Байт – единица хранения цифровой информации, состоящая из 8 -ми бит. • Килобайт – единица хранения цифровой информации 1024 байта. • Килобит – единица хранения цифровой информации 1024 бита.
Биты и байты • Бит – единица хранения цифровой информации, принимающая одно из двух значений {0, 1}. • Байт – единица хранения цифровой информации, состоящая из 8 -ми бит. • Килобайт – единица хранения цифровой информации 1024 байта. • Килобит – единица хранения цифровой информации 1024 бита.
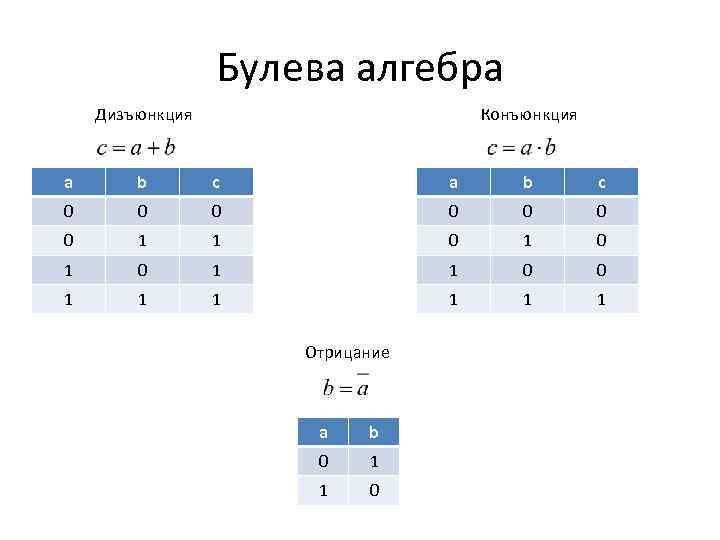 Булева алгебра Дизъюнкция Конъюнкция a b c 0 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 Отрицание a b 0 1 1 0
Булева алгебра Дизъюнкция Конъюнкция a b c 0 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 Отрицание a b 0 1 1 0
 Булева алгебра Булевой алгеброй называется непустое множество A с двумя бинарными операциями конъюнкции и дизъюнкции, унарной операцией отрицания и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы: ассоциативность коммутативность поглощение дистрибутивность дополнение
Булева алгебра Булевой алгеброй называется непустое множество A с двумя бинарными операциями конъюнкции и дизъюнкции, унарной операцией отрицания и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы: ассоциативность коммутативность поглощение дистрибутивность дополнение
 Булева алгебра
Булева алгебра
 Булева алебра Штрих Шеффера Стрелка Пирса Импликация Сложение по модулю 2
Булева алебра Штрих Шеффера Стрелка Пирса Импликация Сложение по модулю 2
 Булева алгебра
Булева алгебра
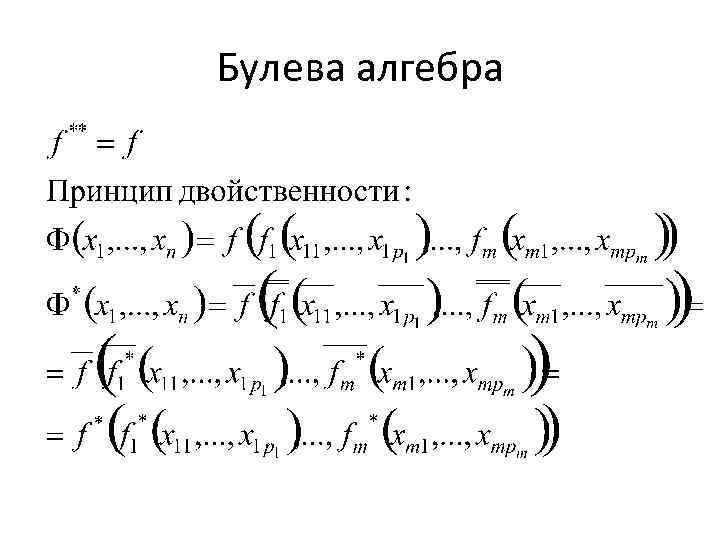 Булева алгебра
Булева алгебра
 Булева алгебра
Булева алгебра
 Булева алгебра
Булева алгебра
 Булева алгебра Система функций называется функционально полной, если любая булева функция может быть записана через формулы этой системы.
Булева алгебра Система функций называется функционально полной, если любая булева функция может быть записана через формулы этой системы.
 Булева алгебра
Булева алгебра
 Булева алгебра
Булева алгебра
 Булева алгебра
Булева алгебра
 Булева алгебра. Замкнутые классы
Булева алгебра. Замкнутые классы
 Вопросы
Вопросы