теорема о взаимности работ.ppt
- Количество слайдов: 22

Теоремы взаимности строительной механики. Теорема о взаимности работ

Dii Dij На рис. показаны действительные и возможные перемещения по направлению обобщённых сил. Суммарная работа внешних обобщённых сил будет равна Зависимости для вычисления действительной и возможной работы внешних обобщённых сил Fi и Fj:

Таким образом, выражение суммарной работы от совместного действия обобщённых сил Fi и Fj в случае, когда первой прикладывается сила Fi, а второй Fj, примет вид: Рассмотрим обратный порядок приложения обобщённых сил: первой приложим статическим способом обобщённую силу Fj, а затем, после её окончательного формирования, – обобщённую силу Fi (рис. в). Суммарная работа внешних обобщённых сил Fi и Fj в этом случае запишется: Значение суммарной работы внешних обобщённых сил Fi и Fj не зависит от последовательности их приложения, т. е. =

Выражение и составляет содержание теоремы о взаимности возможных работ внешних сил: возможная работа i-й обобщённой силы (внешних сил i-го состояния) на перемещениях, вызванных j-й обобщённой силой (внешними силами j-го состояния), равна возможной работе j-й обобщённой силы (внешних сил j-го состояния) на перемещениях, вызванных i-й обобщённой силой (внешними силами i-го состояния). В строительной механике эта теорема носит имя итальянского учёного Энрико Бетти (1823– 1892).

Теорема о взаимности перемещений В состоянии i на него действует сила Fi = 1, а в состоянии j – сила Fj = 1. Зафиксируем возможные перемещения и , возникающие в состояниях i и j от единичных сил. Для состояний сооружения i и j применим теорему о взаимности возможных работ внешних сил : или Соотношение выражает содержание теоремы о взаимности перемещений: перемещение по направлению линии действия i-й единичной обобщённой силы, вызванное j-й единичной обобщённой силой, равно перемещению по направлению линии действия j-й обобщённой силы от i-й единичной обобщённой силы. В строительной механике эта теорема известна как теорема английского физика и механика Джеймса Максвелла (1831– 1879).

Теорема о взаимности реакций На рис. в состояниях i и j показаны реакции в смещаемых связях, а именно: rii – реакция в i-й связи от её смещения на единицу, rjj – реакция в j-й связи от собственного смещения на единицу, rij – реакция в i-й угловой связи от перемещения j-й линейной связи на единицу, rji – реакция в j-й линейной связи от перемещения i-й угловой связи на единицу. К состояниям i и j применим теорему о взаимности возможных работ внешних сил Wext, ij = Wext, ji. В нашем случае: Wext, ij = rii × 0 + rji × 1, Wext, ji = rjj × 0 + rij × 1, rji × 1 = rij × 1, или rij = rji. Равенство является математическим представлением теоремы о взаимности реакций: реакция rij в i-й связи от перемещения jй связи на единицу равна реакции rjiв j-й связи от смещения jй связи на единицу. Принцип взаимности реакций, вытекающей из теоремы Бетти как частный случай, справедлив не только для реакций опорных связей различного типа, но и для реакций внутренних связей (изгибающих моментов, поперечных и продольных сил).
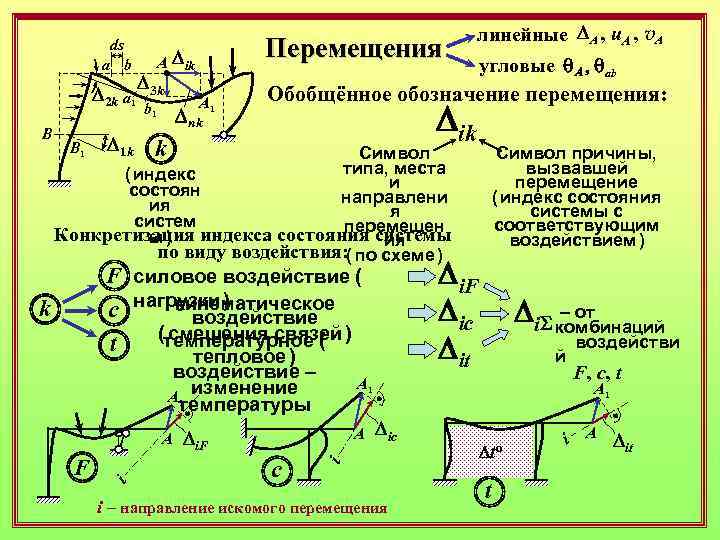
ds a b D 2 k a 1 B B 1 D 1 k Перемещения A Dik D 3 k A 1 b 1 Dnk Dik k кинематическое c нагрузки ) воздействие (температурное ( ) смещения связей t тепловое ) воздействие – изменение А 1 температуры i А Di. F c Di. S – от комбинаций воздействи й F, c, t А 1 Dic i F Символ причины, вызвавшей перемещение ( индекс состояния системы с соответствующим воздействием ) Di. F Dic Dit F силовое воздействие ( А угловые q. A , qab Обобщённое обозначение перемещения: Символ типа, места ( индекс и состоян направлени ия я систем перемещен Конкретизация индекса состояния системы ы ) ия по виду воздействия: ( по схеме ) k линейные DA , u. A , v. A i – направление искомого перемещения Dto t i А Dit
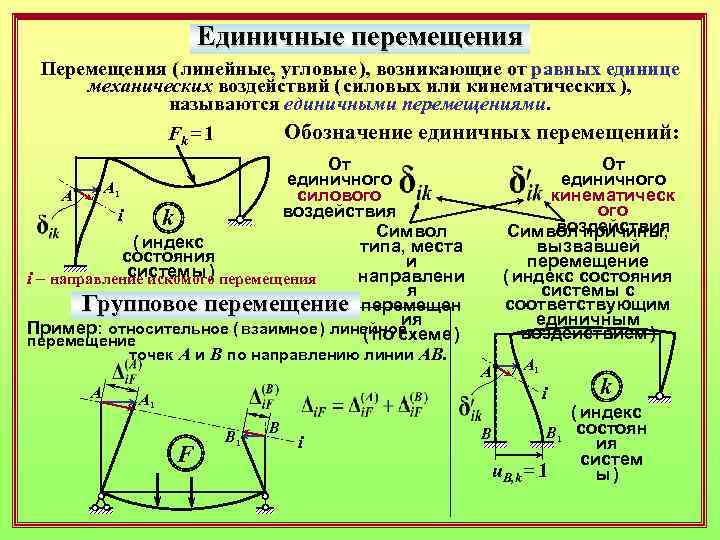
Единичные перемещения Перемещения ( линейные, угловые ), возникающие от равных единице механических воздействий ( силовых или кинематических ), называются единичными перемещениями. Обозначение единичных перемещений: Fk = 1 От единичного А 1 А силового воздействия i k Символ ( индекс типа, места состояния и системы ) перемещения направлени i – направление искомого я Групповое перемещение перемещен ия Пример: относительное ( взаимное ) линейное ( по схеме ) перемещение точек А и В по направлению линии АВ. А От единичного кинематическ ого воздействия Символ причины, вызвавшей перемещение ( индекс состояния системы с соответствующим единичным воздействием ) А А 1 i А 1 F B 1 B i k ( индекс B 1 состоян B ия систем u. B, k = 1 ы )
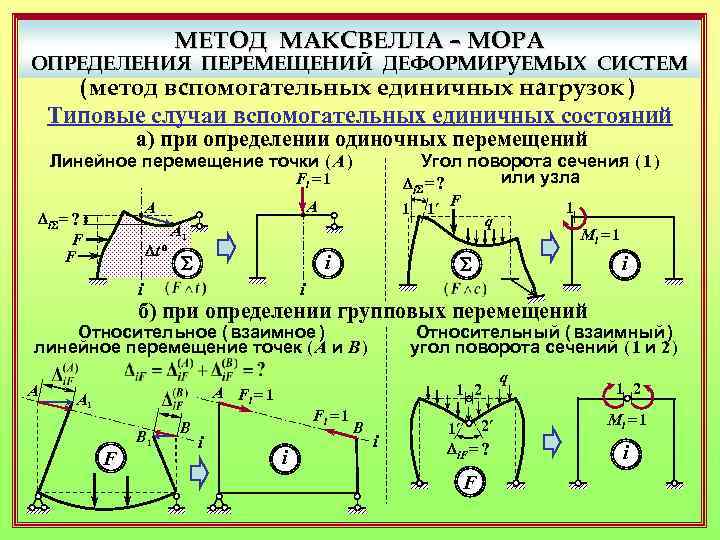
МЕТОД МАКСВЕЛЛА – МОРА ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ ( метод вспомогательных единичных нагрузок ) Типовые случаи вспомогательных единичных состояний а) при определении одиночных перемещений Линейное перемещение точки ( A ) Угол поворота сечения ( 1 ) или узла Di. S= ? Fi = 1 А А Di. S= ? F F Dt 1 1’ F A 1 o S i i 1 q Mi = 1 S i i б) при определении групповых перемещений Относительное ( взаимное ) линейное перемещение точек ( A и В ) А 1 2 А Fi = 1 А 1 F B 1 B Fi = 1 i Относительный ( взаимный ) угол поворота сечений ( 1 и 2 ) i B i 1’ 2’ Di. F= ? F q 1 2 Mi = 1 i
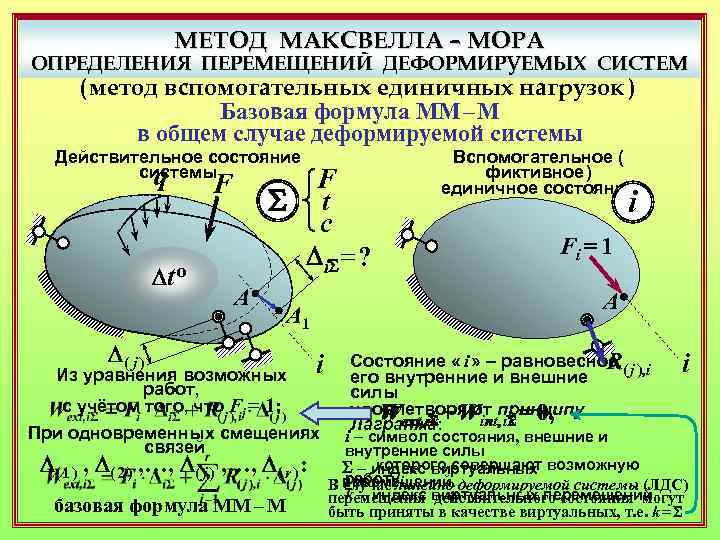
МЕТОД МАКСВЕЛЛА – МОРА ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ ( метод вспомогательных единичных нагрузок ) Базовая формула ММ – М в общем случае деформируемой системы Действительное состояние системы q F S t c Di. S= ? F Dt o A Из уравнения возможных работ, с учётом того, что Fj = 1: i При одновременных смещениях связей D( 1 ) , D( 2 ) , …, D( j ) , …, D( r ) : базовая формула ММ – М i Fi = 1 A A 1 D( j ) Вспомогательное ( фиктивное ) единичное состояние Состояние « i » – равновесное, ( j ), i R его внутренние и внешние силы удовлетворяют принципу Wext, i. S + Wint, i. S = 0, ext, ik ik Лагранжа: i – символ состояния, внешние и i внутренние силы которого совершают возможную S – индекс виртуальных работу; В перемещений. деформируемой системы (ЛДС) случае линейно k – индекс виртуальных перемещений. перемещения действительного состояния могут быть приняты в качестве виртуальных, т. е. k = S
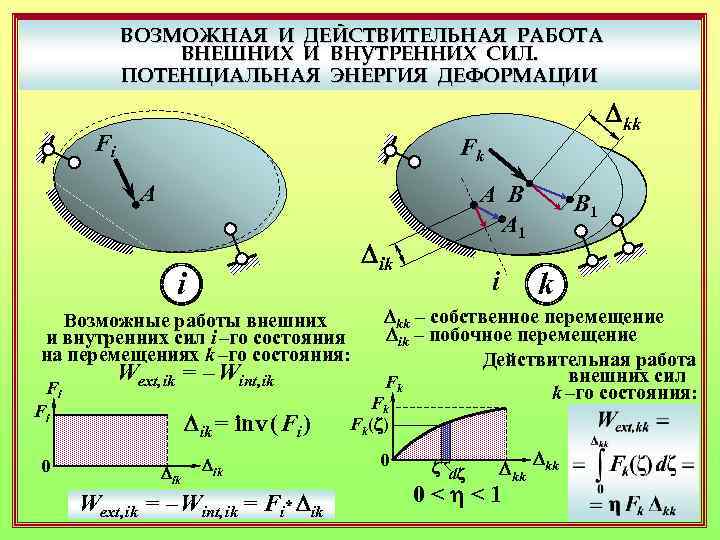
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Fi Fk A Возможные работы внешних и внутренних сил i –го состояния на перемещениях k –го состояния: Wext, ik = – Wint, ik Fi 0 Dik = inv ( Fi ) Dik A B A 1 Dik i Fi Dkk Dik Wext, ik = – Wint, ik = Fi* Dik i B 1 k Dkk – собственное перемещение Dik – побочное перемещение Действительная работа внешних сил Fk k –го состояния: F k Fk(z) 0 z dz Dkk 0<h<1 Dkk

ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Fi Dkk Fk A Dik i A B A 1 B 1 i k – собственное перемещение Dkk Возможные работы внешних Dik – побочное перемещение и внутренних сил i –го состояния Действительная работа на перемещениях k –го состояния: внешних сил Wext, ik = – Wint, ik k –го состояния: Fk Fi Для Fk Fi ЛДС Fk(z) Dik = inv ( Fi ) 0 Dik Wext, ik = – Wint, ik = Fi* Dik Fk(z) 0 U – ПЭУД z dz Dkk h = 1/2 Dkk
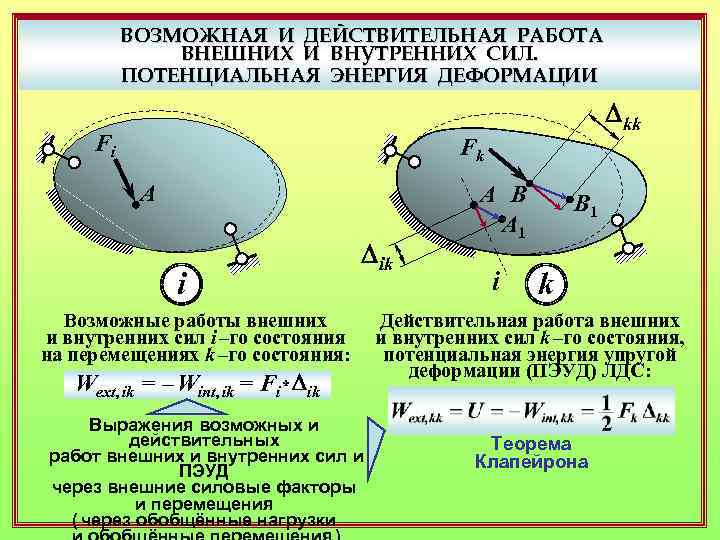
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Fi Dkk Fk A i Dik Возможные работы внешних и внутренних сил i –го состояния на перемещениях k –го состояния: Wext, ik = – Wint, ik = Fi* Dik Выражения возможных и действительных работ внешних и внутренних сил и ПЭУД через внешние силовые факторы и перемещения ( через обобщённые нагрузки A B A 1 i B 1 k Действительная работа внешних и внутренних сил k –го состояния, потенциальная энергия упругой деформации (ПЭУД) ЛДС: Теорема Клапейрона
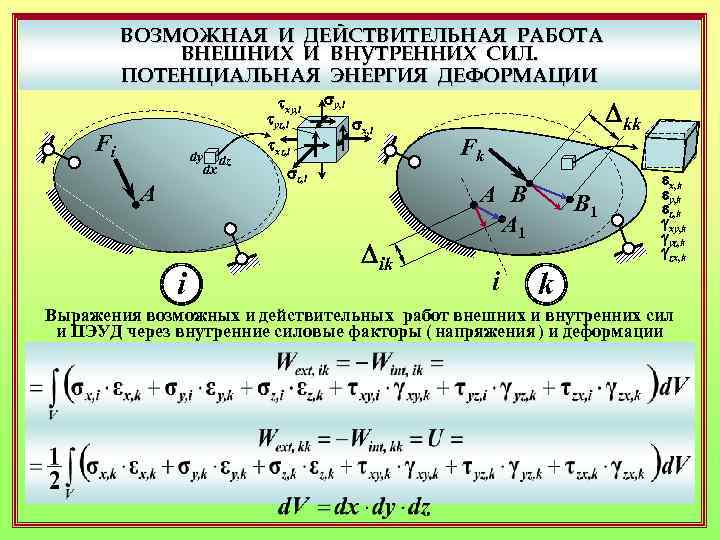
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ txy, i tyz, i Fi dy dz dx A i txz, i sy, i sx, i sz, i Dik Dkk Fk A B A 1 i B 1 ex, k ey, k ez, k gxy, k gyz, k gzx, k k Выражения возможных и действительных работ внешних и внутренних сил и ПЭУД через внутренние силовые факторы ( напряжения ) и деформации
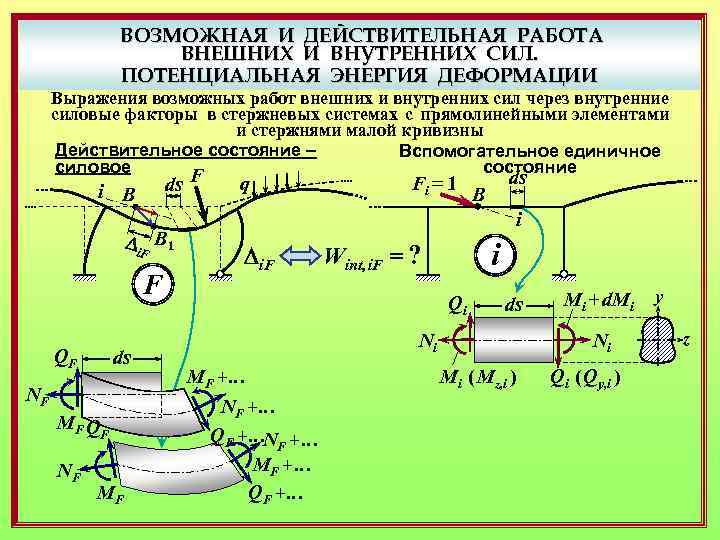
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и внутренних сил через внутренние силовые факторы в стержневых системах с прямолинейными элементами и стержнями малой кривизны Действительное состояние – Вспомогательное единичное силовое состояние ds F i В Di. F В 1 F QF ds NF MF Q NF F MF q Fi = 1 ds В i Di. F i Wint, i. F = ? Qi ds Ni MF +… NF +… QF +…NF +… MF +… QF +… Mi + d. Mi Ni Mi ( Mz, i ) Qi ( Qy, i ) y z
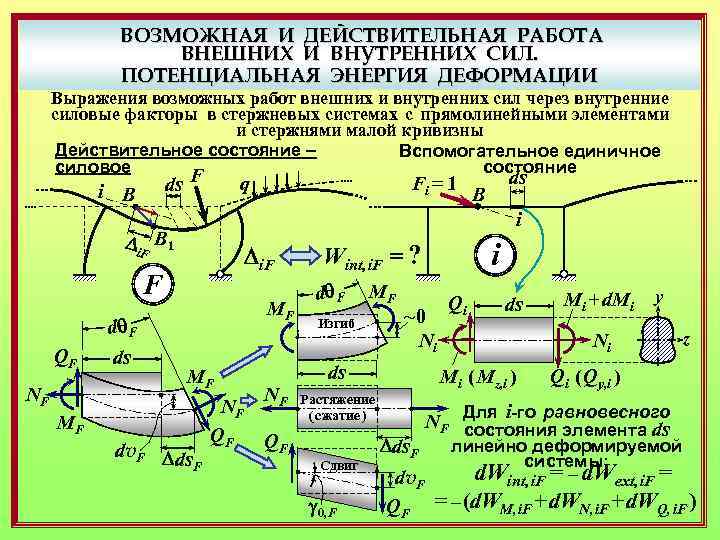
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и внутренних сил через внутренние силовые факторы в стержневых системах с прямолинейными элементами и стержнями малой кривизны Действительное состояние – Вспомогательное единичное силовое состояние ds F i В Di. F F QF NF ds В i Di. F В 1 dq F ds Fi = 1 q MF MF MF dv. F Dds F NF QF NF i Wint, i. F = ? dq F MF Изгиб ~0 Ni ds Сдвиг g 0, F ds Dds. F Mi + d. Mi y Ni Mi ( Mz, i ) Растяжение ( сжатие ) QF Qi z Qi ( Qy, i ) Для i-го равновесного NF состояния элемента ds линейно деформируемой системы: d. Wint, i. F = – d. Wext, i. F = dv. F QF = – (d. WM, i. F + d. WN, i. F + d. WQ, i. F )
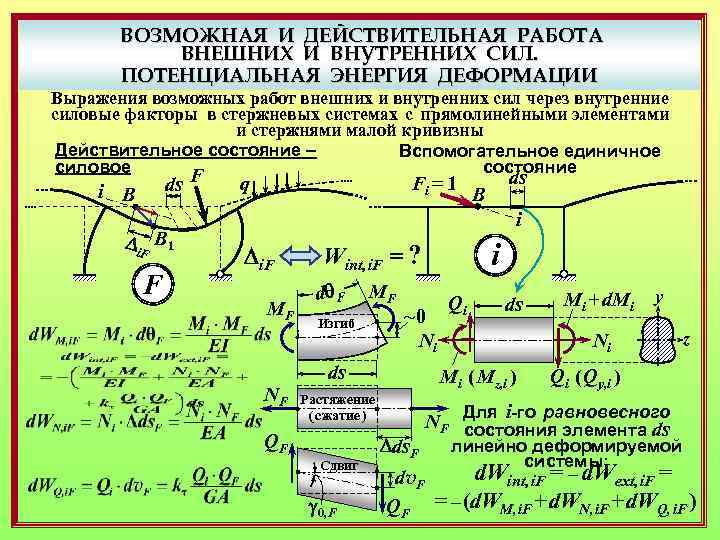
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и внутренних сил через внутренние силовые факторы в стержневых системах с прямолинейными элементами и стержнями малой кривизны Действительное состояние – Вспомогательное единичное силовое состояние ds F i В Di. F В 1 F Fi = 1 q ds В i Di. F MF NF i Wint, i. F = ? dq F MF Изгиб ~0 Ni ds Сдвиг g 0, F ds Dds. F Mi + d. Mi y Ni Mi ( Mz, i ) Растяжение ( сжатие ) QF Qi z Qi ( Qy, i ) Для i-го равновесного NF состояния элемента ds линейно деформируемой системы: d. Wint, i. F = – d. Wext, i. F = dv. F QF = – (d. WM, i. F + d. WN, i. F + d. WQ, i. F )
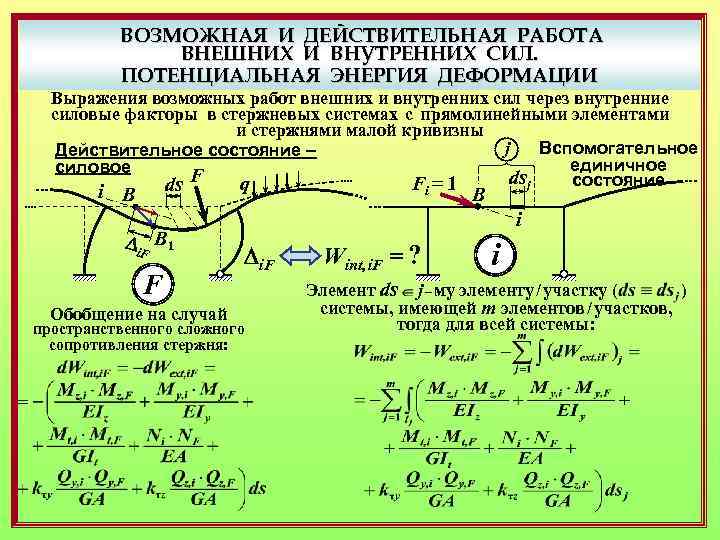
ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и внутренних сил через внутренние силовые факторы в стержневых системах с прямолинейными элементами и стержнями малой кривизны j Вспомогательное Действительное состояние – единичное силовое F dsj состояние Fi = 1 q ds i В В Di. F В 1 F Обобщение на случай i Di. F пространственного сложного сопротивления стержня: Wint, i. F = ? i Элемент ds j – му элементу / участку ( ) системы, имеющей m элементов / участков, тогда для всей системы:
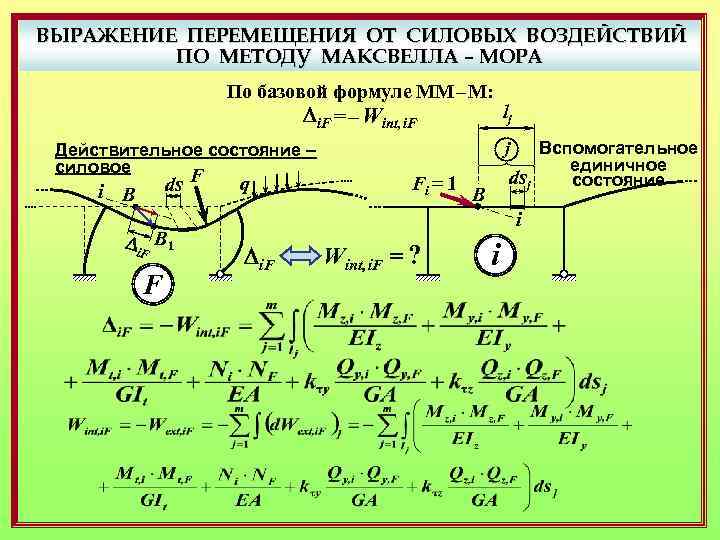
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА По базовой формуле ММ – М: Di. F = – Wint, i. F Действительное состояние – силовое ds F i В Di. F В 1 F q lj j Fi = 1 Вспомогательное единичное dsj состояние В i Di. F Wint, i. F = ? i
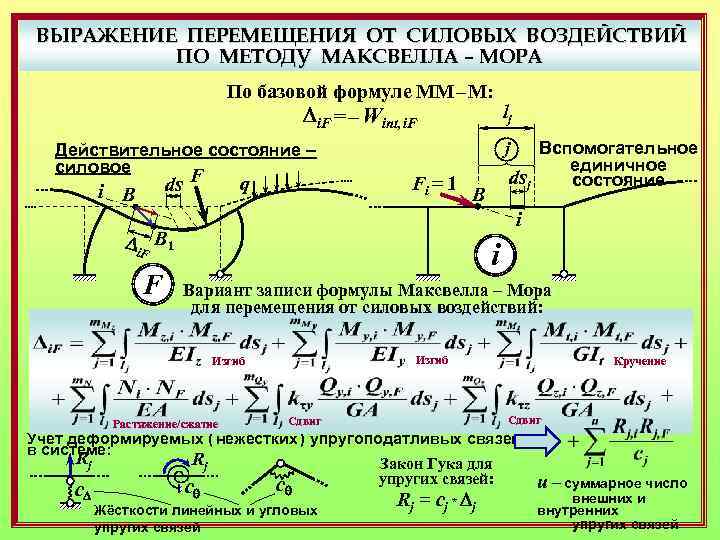
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА По базовой формуле ММ – М: Di. F = – Wint, i. F Действительное состояние – силовое ds F i В q j Fi = 1 Вспомогательное единичное dsj состояние В i Di. F В 1 F lj i Вариант записи формулы Максвелла – Мора для перемещения от силовых воздействий: Изгиб Растяжение/сжатие Кручение Сдвиг Учёт деформируемых ( нежёстких ) упругоподатливых связей в системе: Rj Rj Закон Гука для упругих связей: c c. D cq q Жёсткости линейных и угловых упругих связей Rj = cj * Dj u – суммарное число внешних и внутренних упругих связей
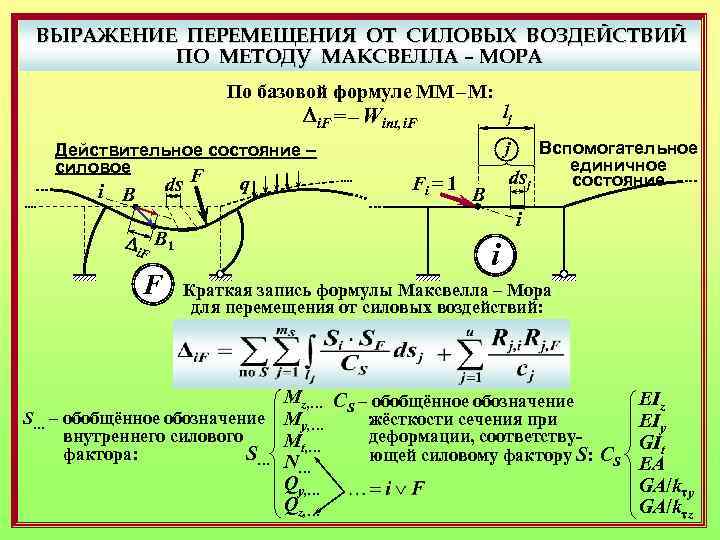
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА По базовой формуле ММ – М: Di. F = – Wint, i. F Действительное состояние – силовое ds F i В Di. F В 1 F q lj j Fi = 1 Вспомогательное единичное dsj состояние В i i Краткая запись формулы Максвелла – Мора для перемещения от силовых воздействий: Mz, … CS – обобщённое обозначение S… – обобщённое обозначение My, … жёсткости сечения при внутреннего силового деформации, соответству. Mt, … фактора: S… N ющей силовому фактору S: CS … Qy, … Qz, … EIz EIy GIt EA GA/kty GA/ktz
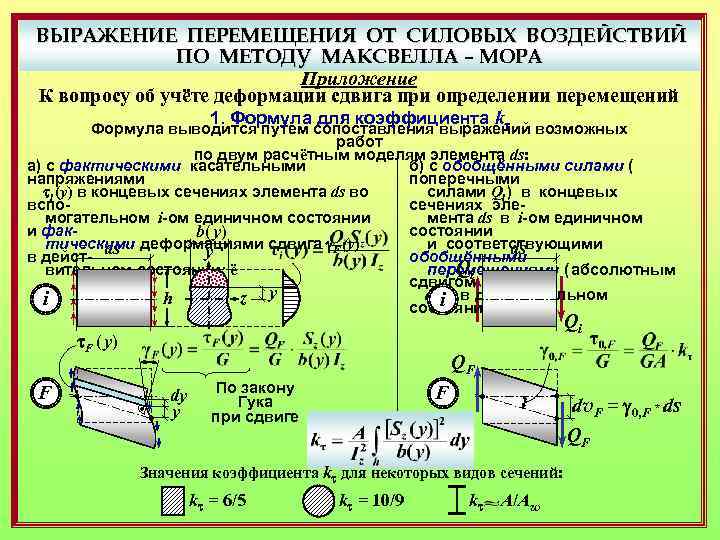
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА Приложение К вопросу об учёте деформации сдвига при определении перемещений 1. Формула для коэффициента kt Формула выводится путем сопоставления выражений возможных работ по двум расчётным моделям элемента ds: а) с фактическими касательными б) с обобщёнными силами ( напряжениями поперечными ti (y) в концевых сечениях элемента ds во силами Qi ) в концевых вспосечениях эле могательном i-ом единичном состоянии мента ds в i-ом единичном и факсостоянии b( y) тическими деформациями сдвига g. F (y) и соответствующими ds y в дейст- ds обобщёнными Qi вительном состоянии: ё перемещениями ( абсолютным сдвигом dvi ) в действительном z y h F i состоянии: Qi t. F ( y) F QF dy y По закону Гука при сдвиге F dv. F = g 0, F * ds QF Значения коэффициента kt для некоторых видов сечений: kt = 6/5 kt = 10/9 kt A/Aw
теорема о взаимности работ.ppt