ТЕОРЕМЫ синусов и косинусов Геометрия 9 класс

ТЕОРЕМЫ синусов и косинусов Геометрия, 9 класс

ПОВТОРЕНИЕ ПО ТЕМЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА

Формулы площади треугольника • S=1/2 ab, где а, в - катеты прямоугольного треугольника • S= 1/2 ah, где а - основание треугольника, h- высота • S= р-полупериметр, а, в, сстороны треугольника

Теорема о площади треугольника • Дано: ABC, BC=a, CA=b, Sплощадь треугольника. Доказать: S=1/2 absin. C Док-во: S=1/2 ah, h=bsin. C. Сл. S=1/2 absin. C

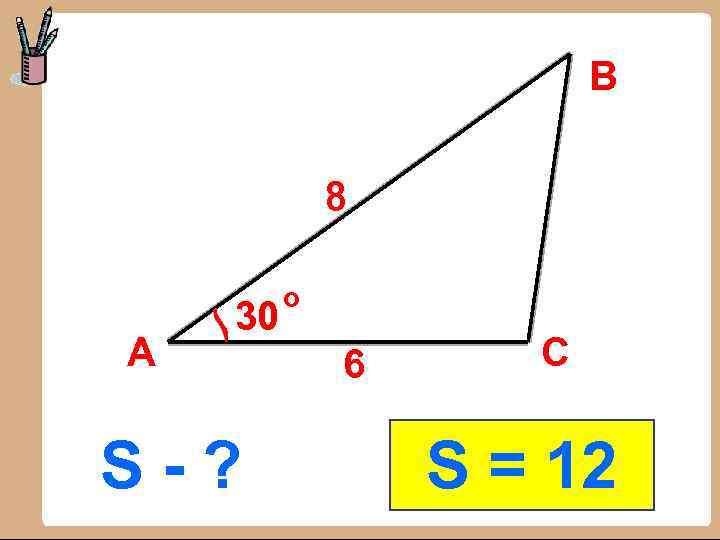В 8 А 30 S-? о 6 С S = 12

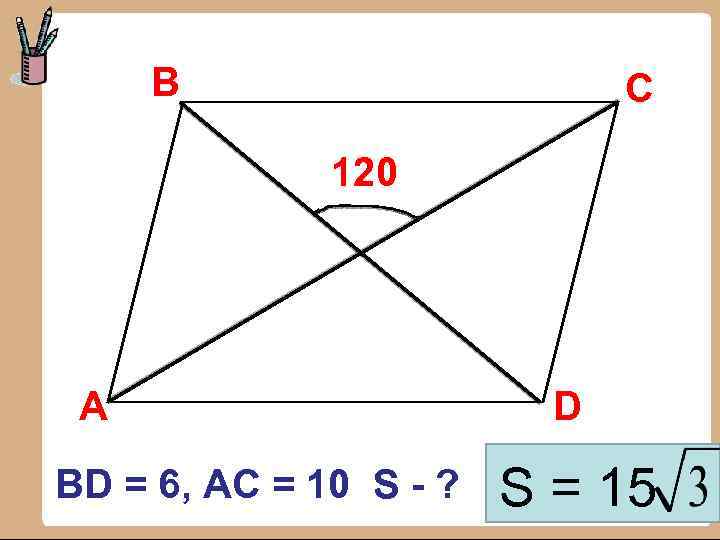В С 120 А BD = 6, AC = 10 S - ? D S = 15

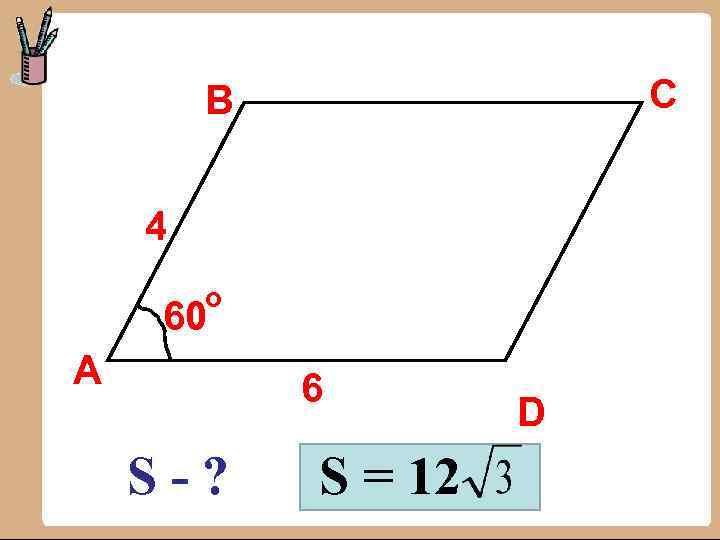C B 4 о 60 А 6 S-? S = 12 D

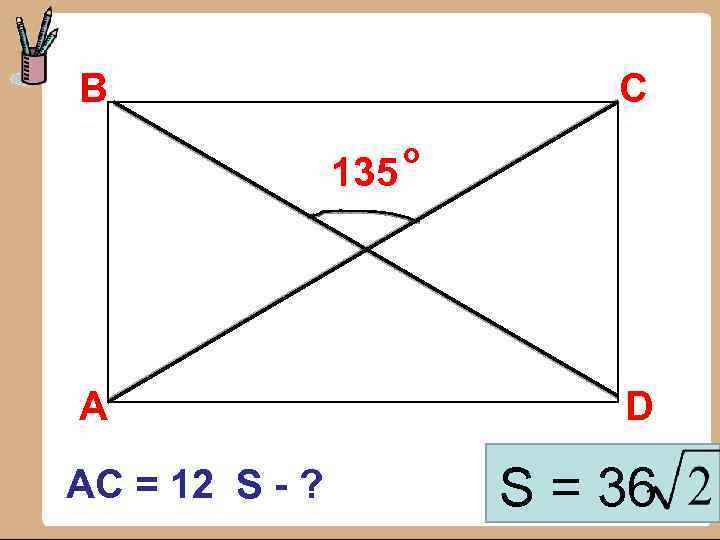В С 135 А AC = 12 S - ? о D S = 36

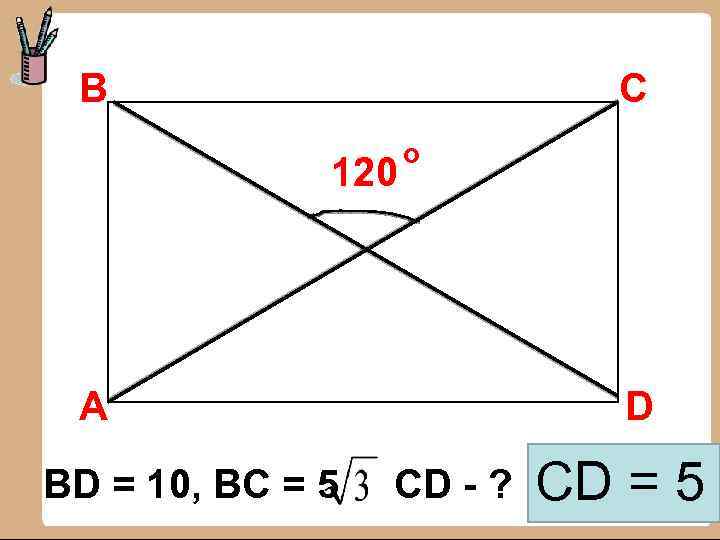В С 120 о А BD = 10, ВC = 5 D CD - ? CD = 5

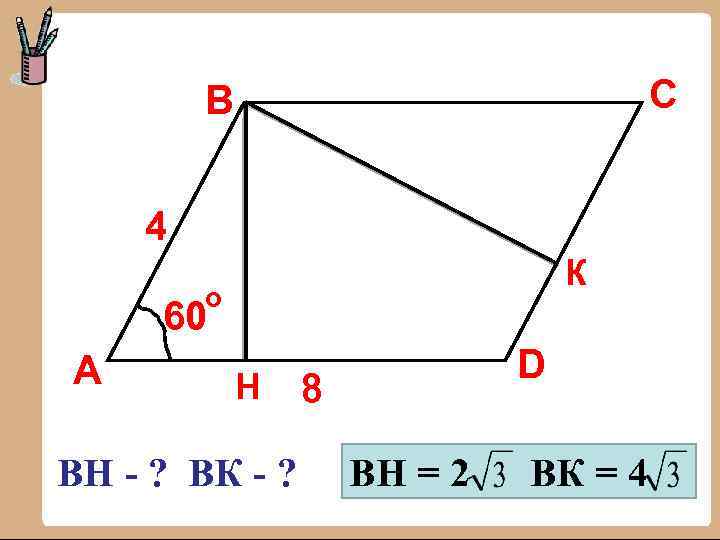C B 4 К о 60 А Н ВН - ? ВК - ? D 8 ВН = 2 ВК = 4

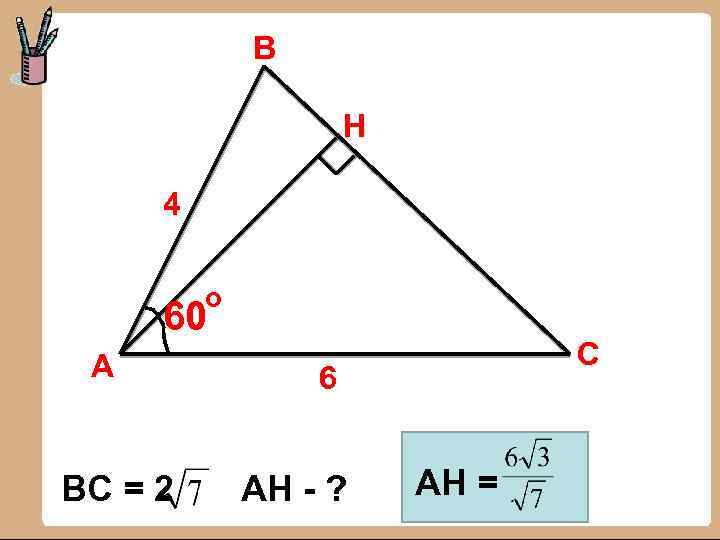В Н 4 о 60 А ВС = 2 С 6 АН - ? АН =

ТЕОРЕМА СИНУСОВ Стороны треугольника пропорциональны синусам противоположных углов

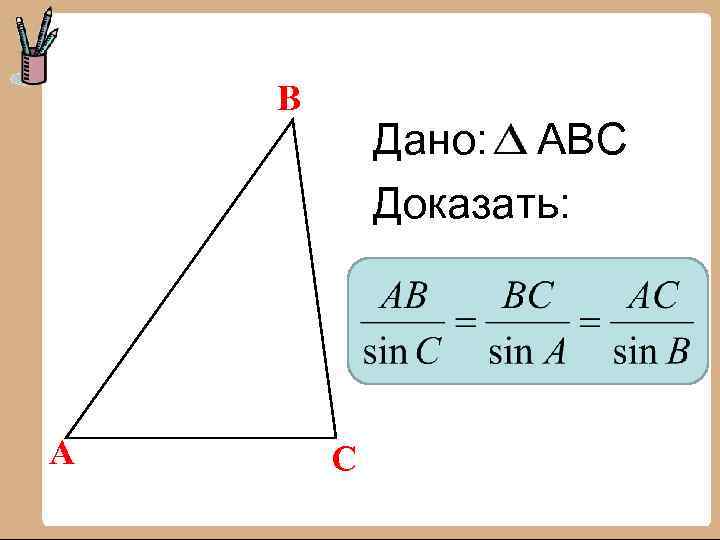В А Дано: АВС Доказать: С

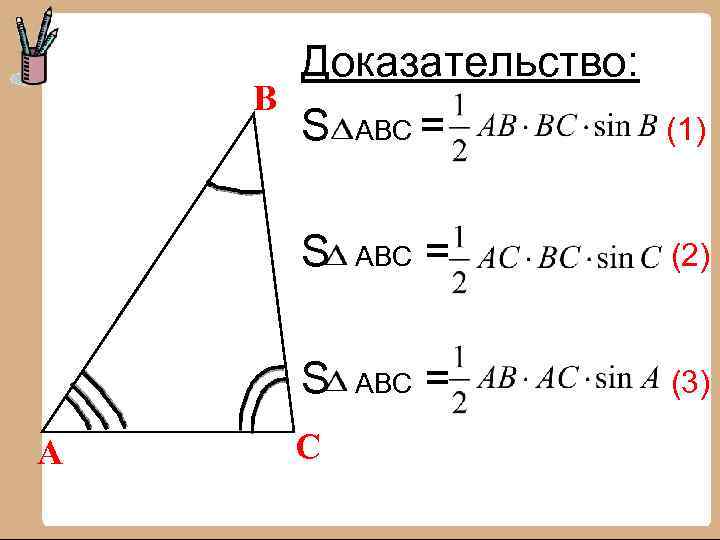Доказательство: В S ABC = (1) S = (2) S А ABC = (3) С

Приравняем равенства (1) и (2), получим = Сократим на , получим =

Приравняем равенства (2) и (3), получим = Сократим на , получим =

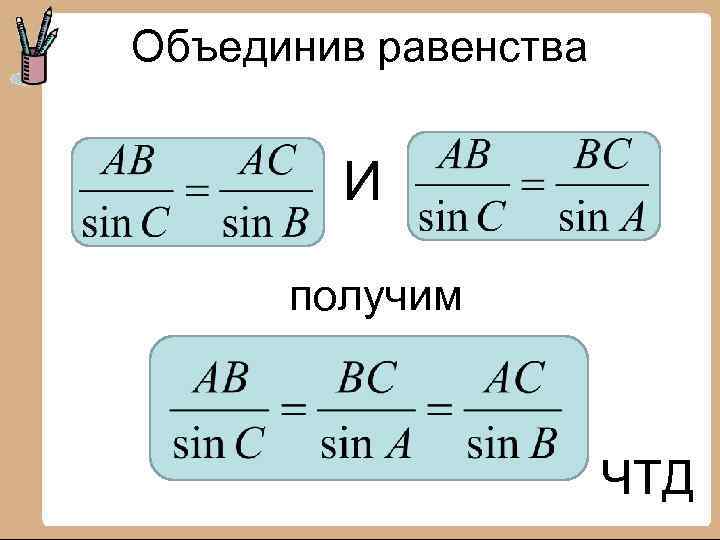Объединив равенства И получим ЧТД

Теорема косинусов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Дано: АВС Доказать:

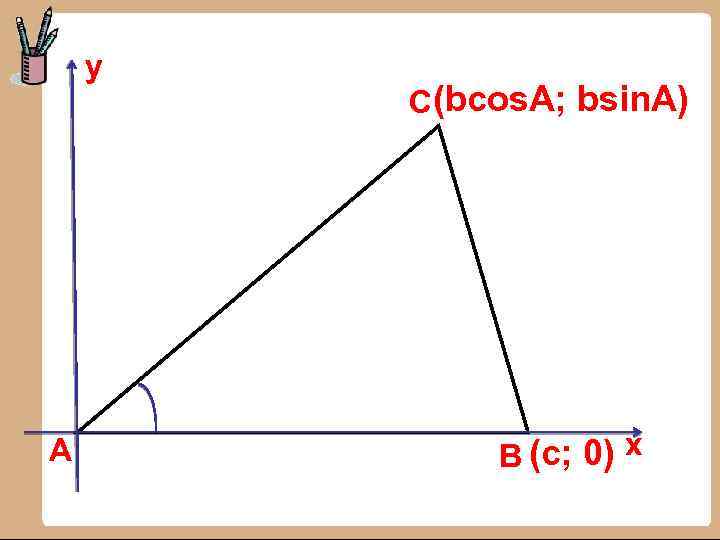у А С(bcos. A; bsin. A) В (с; 0) х

Доказательство: Пусть в треугольнике АВС АВ = с, ВС = а, АС = b. Введем систему координат с началом в точке А. Тогда В (с; 0), С (bcos. A; bsin. A). Найдем расстояние ВС: 2 2 2 2 ВС = а = (bcos. A – c) + b sin A = b cos A + b 2 2 2 sin A - 2 bc cos. A + c = b + c - 2 bc cos. A ЧТД