Теоремы о дифференцируемых функциях Лекция 9

Теоремы о дифференцируемых функциях Лекция № 9

Теорема Ферма Пусть функция f(x) определена на интервале (a, b) и в некоторой точке х0 этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке х0 существует производная, то она равна нулю, т. е. f '(x 0) = 0. Геометрический смысл теоремы Ферма В точке (х0; f(x 0)) касательная к графику функции f(x) || оси Ох 2

Доказательство. Пусть для определенности f(x) в точке х0 имеет наибольшее значение, т. е. для точки х0+ х (a, b) f(x) f(x 0) для х (a, b) y = f(x 0+ x) f(x 0) 0 Поэтому, если х > 0 (x > x 0), то Если же х<0 (x

Теорема Ролля Пусть на [a, b] определена функция f(x), причем: 1) f(x) непрерывна на [a, b]; 2) f(x) дифференцируема на (a, b); 3) f(a) = f(b). Тогда существует точка с (a, b), в которой f '(с) = 0. Доказательство: Т. к. функция f(x) непрерывна на [a, b], то по второй теореме Вейерштрасса она имеет на этом отрезке максимальное значение М и минимальное m, т. е. m f(x) M. Возможны 2 случая: 1) m = M; 2) m < M. 1) m = M = f(x) = const f '(x) = 0 в точке [a, b]. 2) m < M. Т. к. f(a) = f(b) хотя бы одно из двух значений m или M не принимается на концах отрезка [a, b] c (a, b) в которой f(x) принимает наибольшее или наименьшее значение на (a, b). Т. к. f(x) дифференцируема в точке с, из теоремы Ферма следует f '(с) = 0. 4

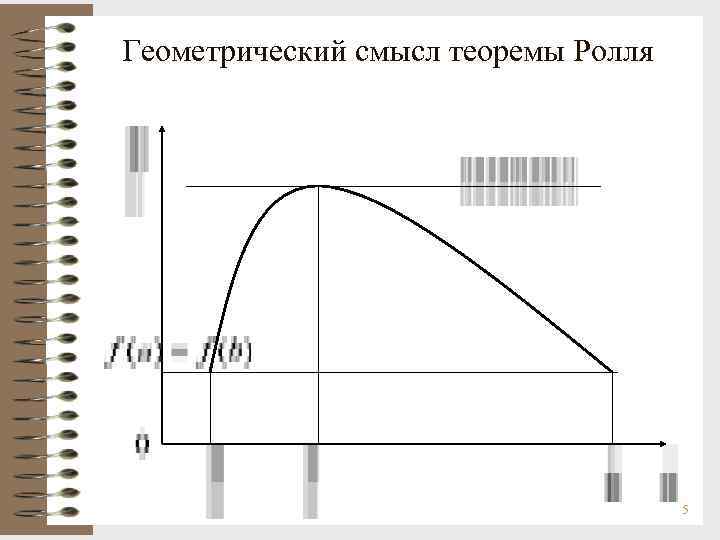Геометрический смысл теоремы Ролля 5

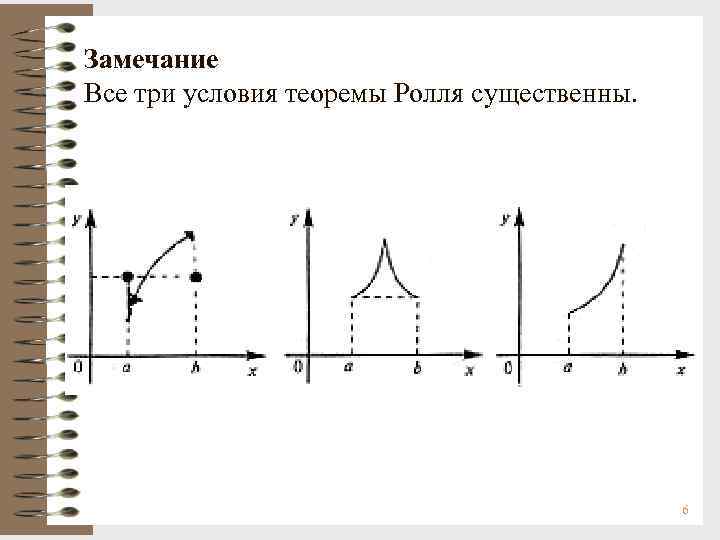Замечание Все три условия теоремы Ролля существенны. 6

Теорема Лагранжа Пусть на [a, b] определена функция f(x), причем: 1) f(x) непрерывна на [a, b]; 2) дифференцируема на (a, b). Тогда существует точка с (a, b) такая, что справедлива формула Доказательство. Введем вспомогательную функцию которая удовлетворяет всем условиям теоремы Ролля с (a, b) такая, что F '(с) = 0. 7

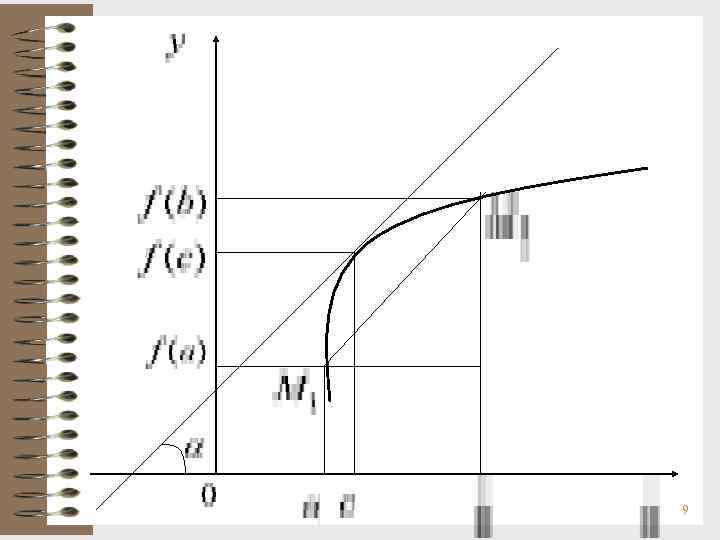
Геометрический смысл теоремы Лагранжа Величина является угловым коэффициентом секущей, проходящей через точки M 1(a; f(a)) и M 2(b; f(b)) графика функции y = f(x). f '(с) – угловой коэффициент касательной к графику функции в точке (с; f(с)). Из теоремы Лагранжа следует, что с такая, что касательная к графику в точке (с; f(с)) || секущей М 1 М 2. 8

9

Замечания Замечание 1. Равенство f(b) – f(a) = f '(с)(b – a), a < c < b, называется формулой Лагранжа или формулой конечных приращений. Замечание 2. Если положить а = х, b = x + x, то получим f(x + x) – f(x) = f '(x + x) x, где 0 < < 1. Теорема Лагранжа лежит в основе многих формул и теорем математического анализа. 10

Исследование поведения функции и построение графиков Теорема (признак монотонности функции). Если функция f(x) дифференцируема на интервале (a, b) и f '(x) 0 (f '(x) 0) на (a, b), то функция f(x) не убывает (не возрастает) на (a, b). Доказательство. Пусть х1 и х2 – произвольные точки из (a, b) и х1 < х2. Тогда имеем: f(x 2) – f(x 1) = f '(с) (x 2 – x 1), с (a, b). По условию f '(с) 0, х2 – х1> 0 f(x 2) – f(x 1) 0 f(x 2) f(x 1), т. е. функция f(x) не убывает на (a, b). Доказательство для случая f '(x) 0 аналогично. Замечание. Точно также можно доказать, что если f '( x)>0 (<0) на (a, b), то f(x) возрастает (убывает) на (a, b). Это условие называется достаточным условием возрастания (убывания) функции f(x) на промежутке (a, b). 11

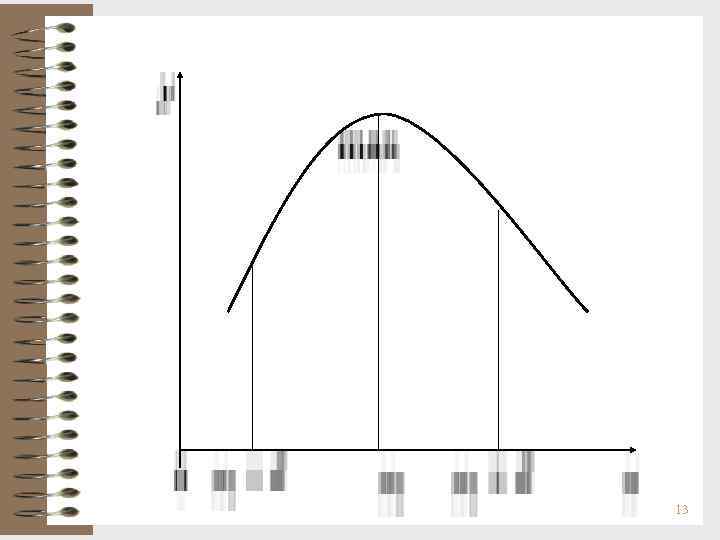
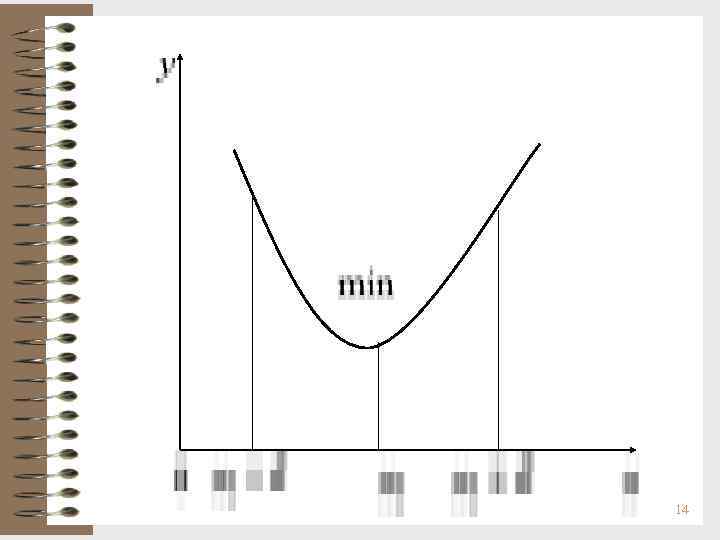
Отыскание точек локального экстремума функции Определение. Точка х0 называется точкой строгого локального максимума (минимума) функции f(x), если для всех х из некоторой -окрестности точки х0 выполняется неравенство f(x) < f(x 0) (f(x) > f(x 0)) при х х0. Локальный максимум (max) и локальный минимум (min) объединяются общим названием локальный экстремум. 12

13

14

Необходимое условие локального экстремума Теорема. Если функция f(x) имеет в точке х0 локальный экстремум и дифференцируема в этой точке, то f '(x 0) = 0. Доказательство: Т. к. в точке х0 функция f(x) имеет локальный экстремум, то существует такой интервал (x 0 – , x 0 + ), в котором значение f(x 0) является наибольшим или наименьшим среди всех других значений этой функции. Тогда по теореме Ферма f '(x 0) = 0. Замечание. Понятие экстремума носит локальный характер в том смысле, что неравенство f(x) < f(x 0) (f(x) > f(x 0)) может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки х0. Функция может иметь несколько локальных максимумов и локальных минимумов, причем может так случиться, что иной локальный максимум окажется меньше 15 какого-то локального минимума.

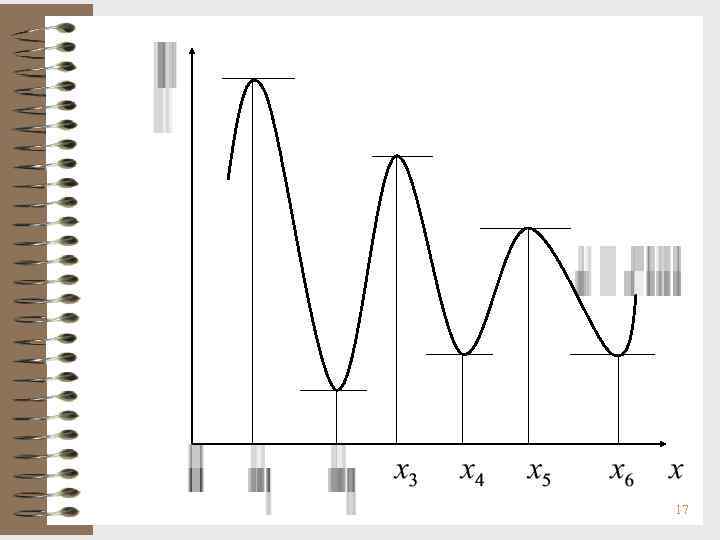
Геометрический смысл теоремы Если х1, х2, х3, х4, х5, х6 – точки локального экстремума и в соответствующих точках графика существуют касательные, то эти касательные || оси Ох. Точки, в которых f '(x) = 0, называют стационарными, критическими или точками возможного экстремума. 16

17

Первое достаточное условие локального экстремума Теорема. Пусть функция f(x) дифференцируема в некоторой окрестности точки х0. Если при переходе через эту точку слева направо производная f '(x) меняет знак с “+” на “ ” ( c “ ” на “+”), то в точке х0 функция f(x) имеет локальный максимум (минимум). Если же f '(x) не меняет знак в -окрестности точки х0, то данная функция не имеет локального экстремума в точке х0. 18

Доказательство. Пусть при переходе через точку х0 производная меняет знак с “+” на “ ” в интервале (х0 , х0 + ). Возьмем произвольную точку х (х0 , х0), х х0; на отрезке [x, x 0] выполняются условия: f(x 0) f(x) = f '(с)(х0 х), с (х, х0). Т. к. f '(x)>0 при х (х0 , х0) и х0 >х, получим f(x) < f(x 0). Возьмем точку х (х0, х0 + ), х х0; на отрезке [x 0, x] выполняются условия: f(x) f(x 0) = f '(с)(х х0), с (х0, х). Т. к. f '(х) < 0 при х (х0, х0 + ) и х0 < x, получим f(x 0) > f(x). в -окрестности точки х0 выполняется условие локального максимума. Случай локального минимума доказывается аналогично. Если же f '(x) не меняет знака при переходе через точку х0, то она является монотонной на интервале (х0 , х0 + ) не имеет локального экстремума в точке х0. 19

Замечание. Теорема остается справедливой, если функция f(x) в самой точке х0 не дифференцируема, а только непрерывна. Например, функция f(x) = |x| в точке х = 0 непрерывна, но не дифференцируема. Необходимое условие экстремума: Для того, чтобы функция y = f(x) имела экстремум в точке х0, необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала. Такие точки называют критическими (или стационарными). 20

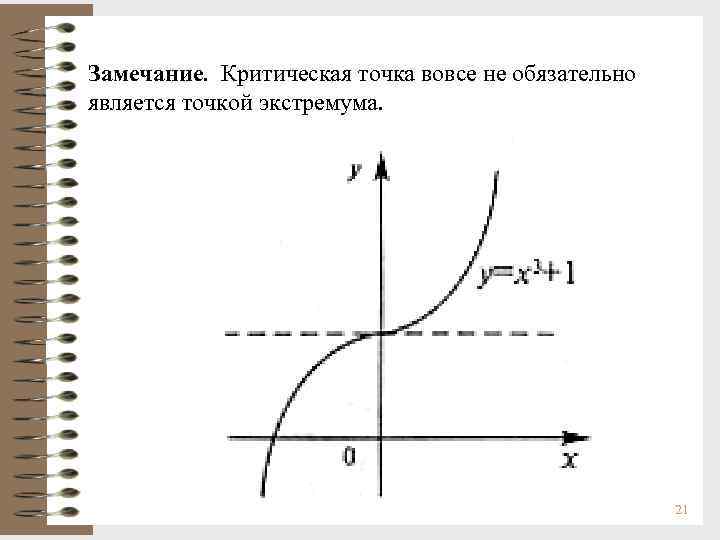Замечание. Критическая точка вовсе не обязательно является точкой экстремума. 21

Второе достаточное условие экстремума Теорема. Если первая производная f '(x) дважды дифференцируемой функции равна нулю в некоторой точке x 0, а f''(x 0) в этой точке > 0, то точка x 0 есть точка минимума функции f(x); если f ''(x 0) < 0, то x 0 – точка максимума. Доказательство. Пусть f '(x 0) = 0, а f'' (x 0) > 0. Это означает, что f ''(x) = (f '(x))' > 0 также и в некоторой окрестности точки х0, т. е. f '(x) возрастает на на некотором интервале (a, b), содержащим точку х0. Но f '(x 0) = 0, следовательно, на интервале (а, х0) f '(x 0) < 0, а на интервале (х0, b) f '(x 0) > 0. т. е. f '(x) при переходе через точку х0 меняет знак с минуса на плюс, т. е. х0 – точка 22 минимума.

Схема исследования функции y = f(x) на экстремум: 1. Найти производную f '(x). 2. Найти критические точки функции, в которых производная f '(x) = 0 или не существует. 3. Исследовать знак производной справа и слева от каждой критической точки и сделать вывод о наличии экстремумов. ( 3 a. Найти вторую производную f ''(x) и определить ее знак в каждой критической точке. Сделать вывод о наличие экстремумов в критических точках. ) 4. Найти экстремумы функции. Схема для отыскания наибольшего и наименьшего значений на отрезке [a, b]: 1. Найти производную f '(x). 2. Найти критические точки функции, в которых f '(x) = 0 или не существует. 3. Найти значения функции в точках экстремума и на концах отрезка [a, b] и выбрать из них наибольшее и наименьшее. 23

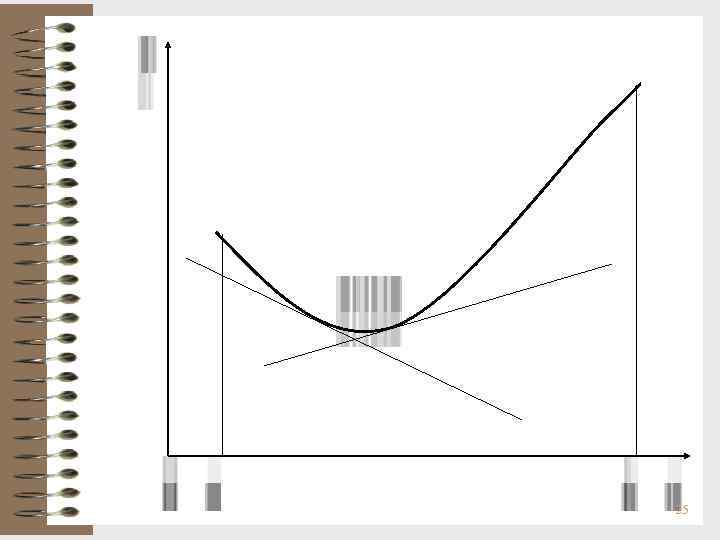
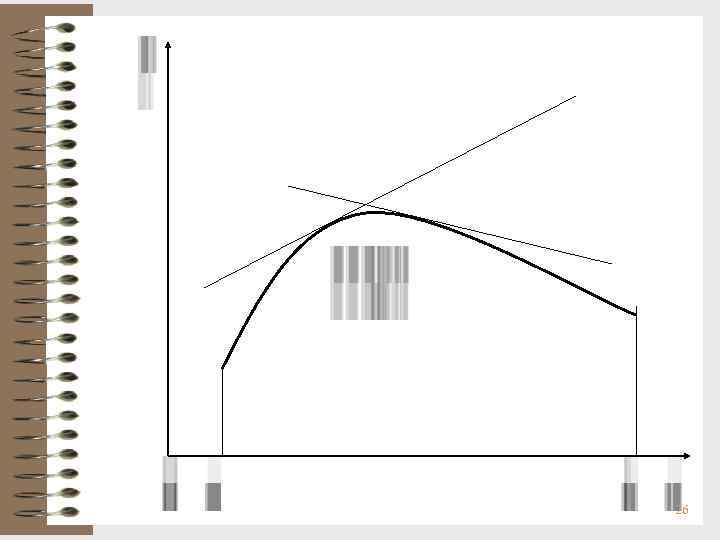
Направление выпуклости и точки перегиба графика функции Определение 1. График функции y = f(x) имеет на (a, b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на интервале (a, b). Замечание. Функцию, выпуклую вниз часто называют выпуклой, а функцию, выпуклую вверх – вогнутой. 24

25

26

Теорема. Если функция y = f(x) имеет на интервале (a, b) вторую производную и f ''(x) > 0 (f ''(x) < 0) во всех точках (a, b), то график функции y = f(x) имеет на (a, b) выпуклость, направленную вниз (вверх). Определение 2. Точка М(x 0; f(x 0)) называется точкой перегиба графика функции y = f(x), если в точке М график имеет касательную, и существует такая окрестность точки x 0, в пределах которой график функции y = f(x) слева и справа от точки х0 имеет разные направления выпуклости. 27

28

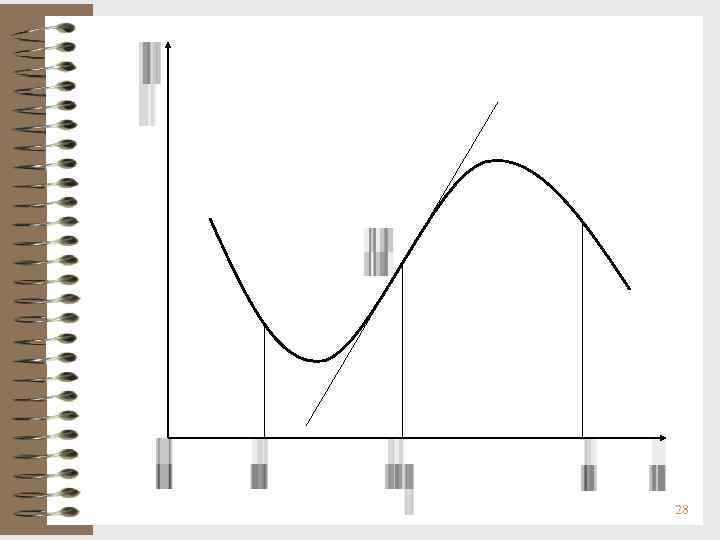
Теорема (необходимое условие точки перегиба). Пусть график функции y = f(x) имеет перегиб в точке M(x 0; f(x 0)) и пусть функция y = f(x) имеет в точке х0 непрерывную вторую производную. Тогда f ''(x) в точке хо обращается в нуль, т. е. f ''(x 0) = 0. Доказательство: Допустим обратное, т. е. f ''(x 0) 0. Тогда либо f ''(x) > 0, либо f ''(x) < 0. Но график функции имеет определенное направление выпуклости в этой окрестности, что противоречит условию теоремы. Точки графика, для которых выполняется условие f ''(x 0) = 0, называются критическими. 29

Терема (достаточное условие точки перегиба). Пусть функция y = f(x) имеет вторую производную в некоторой окрестности точки х0. Тогда, если в пределах указанной окрестности f ''(x) имеет разные знаки слева и справа от точки хо, то график y = f(x) имеет перегиб в точке M(x 0; f(x 0)). Доказательство. Учтем, что направление выпуклости слева и справа от точки х0 являются различными. Согласно определению 2 это и означает наличие перегиба графика функции y = f(x) в точке х0. Замечание. Теорема остается верной, если f(x) имеет вторую производную в некоторой окрестности точки х0, за исключением самой точки х0, и существует касательная к графику функции в точке М. Тогда, если в пределах указанной окрестности f ''(x) имеет разные знаки слева и справа от точки х0, то график функции y = f(x) имеет перегиб в точке М(x 0; f(x 0)). 30

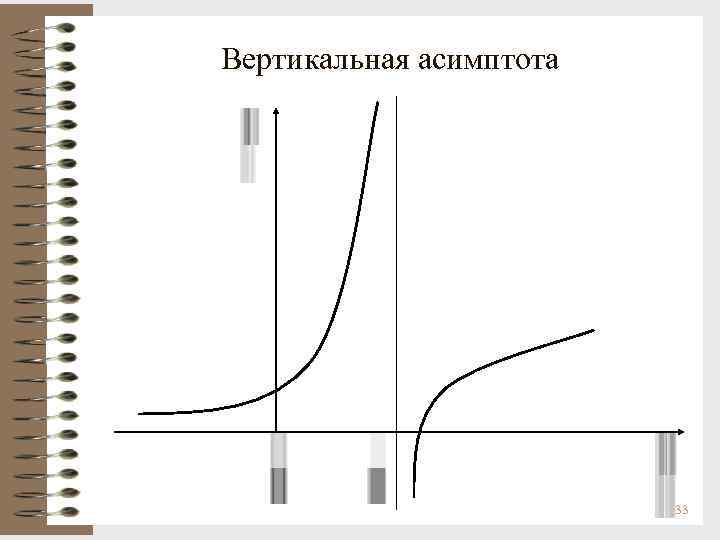
Асимптоты графика функции При исследовании поведения функции на бесконечности, т. е. при х или вблизи точек разрыва 2 -го рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называются асимптотами. Существуют три вида асимптот: вертикальные, горизонтальные и наклонные. Определение 3. Прямая х = х0 называется вертикальной асимптотой графика функции y = f(x), если хотя бы одно из предельных значений равно + или 31

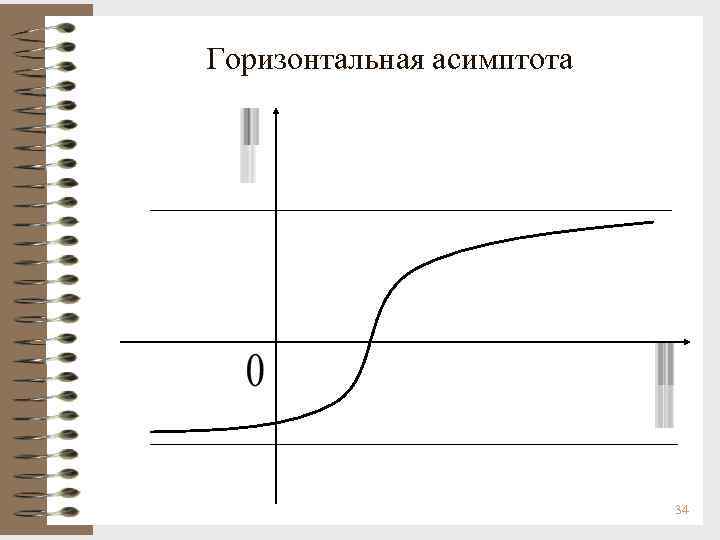
Определение 4. Прямая у = А называется горизонтальной асимптотой графика функции y = f(x) при х + (х ), если Определение 5. Прямая y = kx + b (k 0) называется наклонной асимптотой графика функции y = f(x) при х + (х ), если функцию f(x) можно представить в виде f(x) = kx + b + (x), где (х) 0 при х + (х ). Определение 6. Асимптотой графика функции y = f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат (в этом геометрический смысл асимптоты). 32

Вертикальная асимптота 33

Горизонтальная асимптота 34

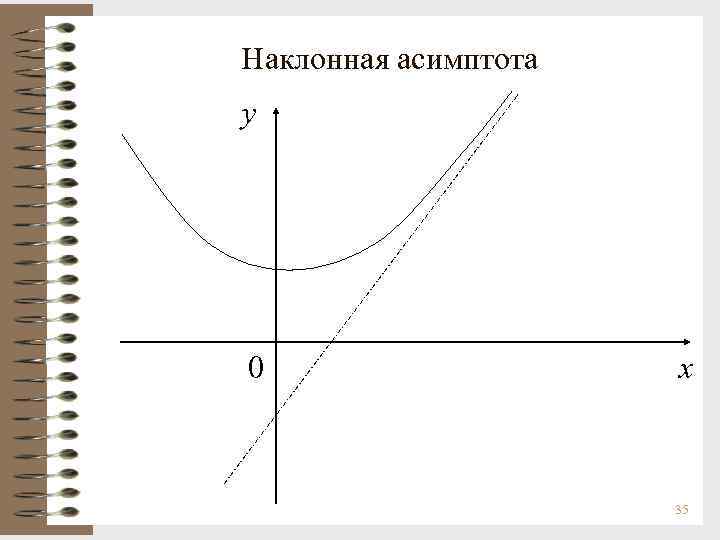Наклонная асимптота y 0 x 35

Рассмотрим способ отыскания наклонной асимптоты. Разделим f(x)=kx+b+ (x) на х и перейдем к пределу при х + , получим Итак, Далее, получим : Таким образом: 36

В случае горизонтальной асимптоты угловой коэффициент k = 0. Практически целесообразно искать асимптоты в следующем порядке: 1) вертикальные асимптоты; 2) горизонтальные асимптоты; 3) наклонные асимптоты. 37

Общая схема исследования функций и построения их графиков 1. Найти область определения функции. 2. Исследовать функцию на четность-нечетность. 3. Найти вертикальные асимптоты. 4. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты. 5. Найти экстремумы и интервалы выпуклости функции и точки перегиба. 6. Найти точки пересечения с осями координат и некоторые дополнительные точки, уточняющие график. 38

Правило Лопиталя Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле. Доказательство. Пусть f(x) и g(x) – бесконечно малые в точке x 0. Для простоты будем предполагать, что f(x) и g(x) непрерывны в точке x 0 вместе со своими производными. 39

Применим к функциям f(x) и g(x) теорему Лагранжа на отрезке [x, x 0]. где Учитывая непрерывность производных, получаем (1). Пример. Сравнить бесконечно большие функции : 40