Теорема Стюарта. Круги Аполлония. Работа ученицы 9 В класса Черней Ксении
• Отрезок, соединяющий вершину треугольника с точкой на противолежащей стороне или ее продолжении, называется чевианой.
Теорема Стюарта. • Теорема была сформулирована М. Стюартом (1746), но, возможно, была известна Архимеду. Иногда ее называют теоремой Аполлония. • Из теоремы Стюарта, в частности, выводятся формулы для длины медианы и биссектрисы треугольника.
Теорема Стюарта. Формулировка • Теорема: Формула, связывающая длину чевианы, проведенной к основанию треугольника (точнее, ее квадрат), с длинами отрезков, на которые она делит основание, и боковыми сторонами:
Доказательство Дано: ABC DЄBC Доказать: Доказательство: Для доказательства используем теорему косинусов: a 2= b 2+c 2 – 2 bc*cos. A , откуда cos. A= Для ABC: cos. B= Для ABD: cos. B=
Приравниваем правые части и домнажаем на 2 AB = По свойству пропорций: , то есть Теорема доказана.
Вычисление медианы треугольника: • Дано: • ABC • a, b, c- стороны треугольника • ac , ab - части a • ma- медиана к стороне a • Найти: • ma
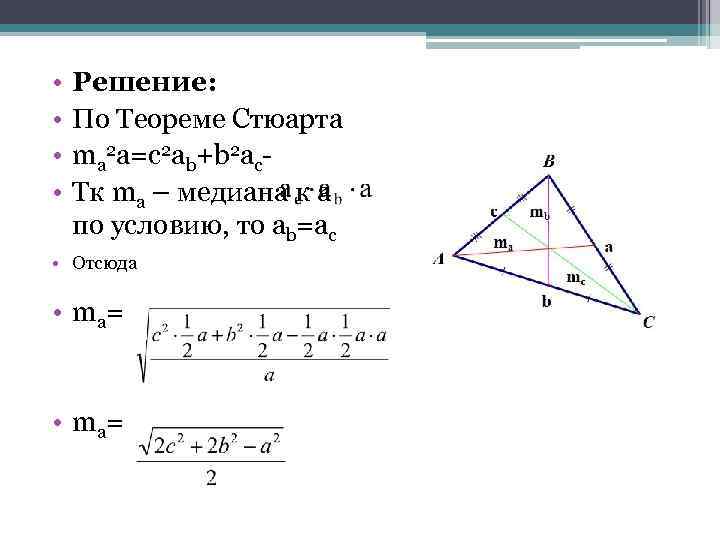
• • Решение: По Теореме Стюарта ma 2 a=c 2 ab+b 2 ac. Тк ma – медиана к а по условию, то ab=ac • Отсюда • ma=
Вычисление биссектрис треугольника: • Дано: • ABC • a, b, c- стороны треугольника • ac , ab - части a • la- биссектриса к стороне a • Найти: • la
• la 2 a=c 2 ab+b 2 ac-abaca (по Теореме Стюарта • la 2= • По свойству биссектрис: • , откуда • ab= ; ac= • la 2= • то есть la=
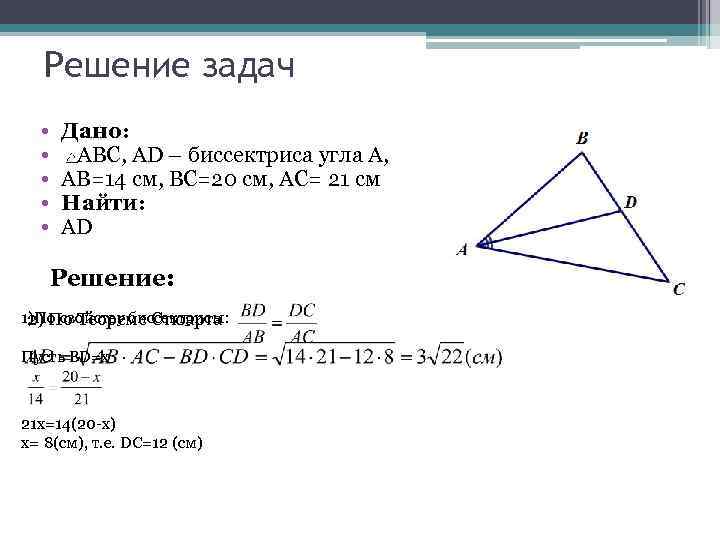
Решение задач • • • Дано: ABC, AD – биссектриса угла A, AB=14 см, BC=20 см, AC= 21 см Найти: AD Решение: 1)По свойству биссектрисы: 2) По Теореме Стюарта Пусть BD=x 21 x=14(20 -x) x= 8(см), т. е. DC=12 (см)
• Дано: • ABC, AD – медиана к BC, AB=12 см, BC=16 см, AC= 20 см • Найти: • AD Решение: Медиана делит сторону пополам: BD=DC=8(см) По теореме Стюарта:
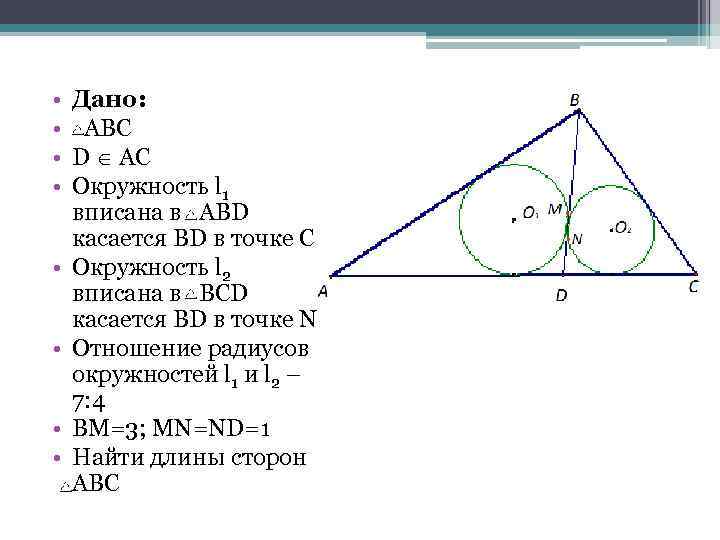
• • Дано: ABC D Î AC Окружность l 1 вписана в ABD касается BD в точке С Окружность l 2 вписана в BСD касается BD в точке N Отношение радиусов окружностей l 1 и l 2 – 7: 4 BM=3; MN=ND=1 Найти длины сторон ABC
• 1)Пусть AK=AL=x, CP=CQ=y. Тогда • p ABD=x+5 и • p BCD=y+5 • 2) • • , откуда • 3 xy-13 x+27 y-5=0; • 3) По Теореме Стюарта из ABC
• 4) Из (2) и (3) составляем систему 3 xy-13 x+27 y-5=0; • Откуда получаем, что x=7 и y=2 • Отсюда AB=10, BC=6, AC=12
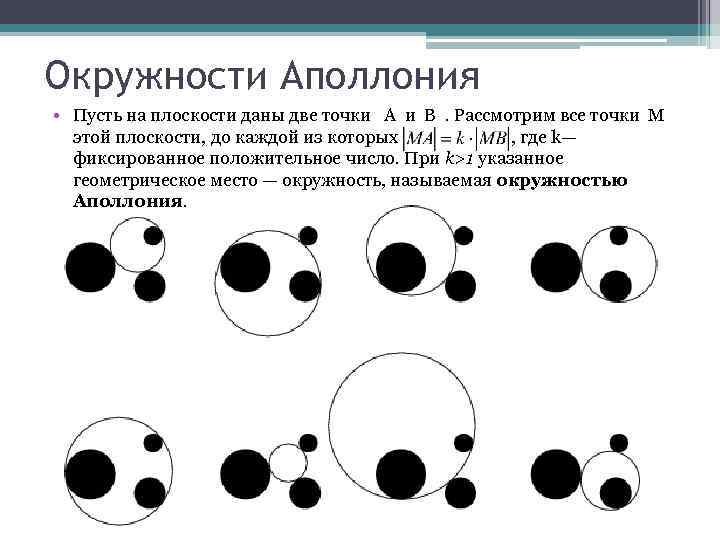
Окружности Аполлония • Пусть на плоскости даны две точки А и В . Рассмотрим все точки М этой плоскости, до каждой из которых , где k— фиксированное положительное число. При k>1 указанное геометрическое место — окружность, называемая окружностью Аполлония.
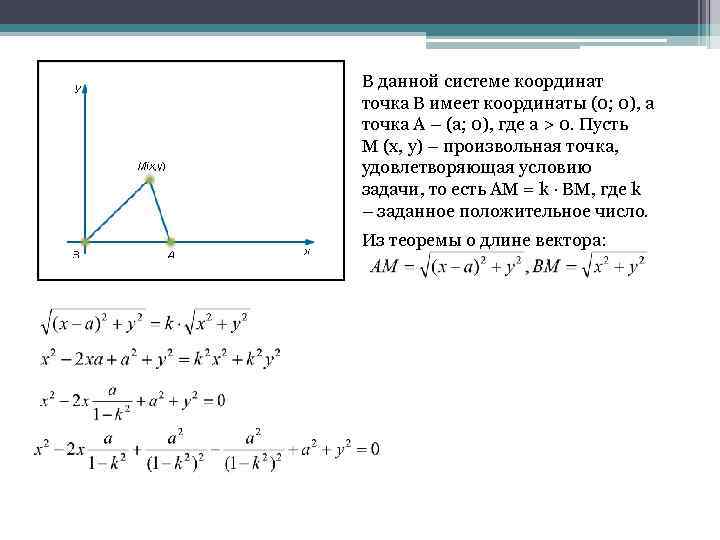
В данной системе координат точка B имеет координаты (0; 0), а точка A – (a; 0), где a > 0. Пусть M (x, y) – произвольная точка, удовлетворяющая условию задачи, то есть AM = k · BM, где k – заданное положительное число. Из теоремы о длине вектора:
Выделив полный квадрат, получим: M Это уравнение окружности с центром в точке и радиуса Полученная окружность называется окружность Аполлония, носит имя древнегреческого геометра Аполлония , решившего поставленную задачу чисто геометрическим методом.
Скачать презентацию Теорема Стюарта Круги Аполлония Работа ученицы 9 В
Теорема Стюарта.pptx